函数的证明与推理课件
- 格式:docx
- 大小:37.68 KB
- 文档页数:5








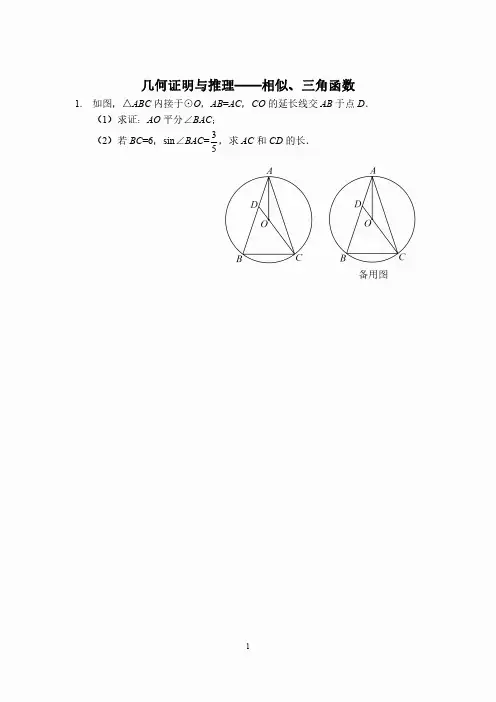
几何证明与推理——相似、三角函数1.如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.(1)求证:AO平分∠BAC;(2)若BC=6,sin∠BAC=35,求AC和CD的长.备用图2.如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.(1)判断直线DF与⊙O的位置关系,并说明理由;(2)当∠A=30°,CF=2时,求⊙O的半径.3.如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.(1)求证:DB=DE;(2)若AB=12,BD=5,求⊙O的半径.4.如图,点E 在以AB 为直径的⊙O 上,点C 是BE ︵的中点,过点C 作CD ⊥AE ,交AE 的延长线于点D ,连接BE 交AC 于点F .(1)求证:CD 是⊙O 的切线;(2)若cos ∠CAD =45,BF =15,求AC 的长.5.如图,AB 是⊙O 的直径,点C 在⊙O 上,AD 平分∠CAB ,BD 是⊙O 的切线,AD 与BC 相交于点E ,与⊙O 相交于点F ,连接BF .(1)求证:BD =BE ;(2)若DE =4,BD =25,求AE 的长.6.如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,且四边形BCOE是平行四边形.(1)BC是⊙O的切线吗?若是,给出证明;若不是,请说明理由.(2)若⊙O半径为1,求AD的长.7.如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,过点D作半圆O的切线交AC于点E.(1)请猜想DE与AC的位置关系,并说明理由;(2)当AB=6,BD=2时,求DE的长.8.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.(1)求证:BC是⊙O的切线;(2)连接AF,BF,求∠ABF的度数.9.如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.(1)求证:直线MN是⊙O的切线;(2)若AD=4,AC=5,求⊙O的直径.10.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,3sin5A 时,求AF的长.11.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC,AC.(1)求证:AC平分∠DAO;(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数;②若⊙O的半径为22,求线段EF的长.。

函数的证明与推理课件
函数的证明与推理
在数学领域中,函数的证明与推理是一项重要的技能。
通过证
明和推理,我们可以得到对函数性质的深刻理解,并在解决数学
问题时做出精确的推断和推理。
本课件将介绍函数的证明与推理
的基本概念和方法,帮助读者提升这一方面的技能。
一、函数的定义与特性
在开始论述函数的证明与推理之前,我们先来回顾一下函数的
基本定义和特性。
函数是一个自变量和因变量之间的映射关系,通常表示为f(x),其中x为自变量,f(x)为因变量。
函数有着以下几个重要特性:
1. 函数的定义域与值域:定义域是指自变量的集合,值域是指
函数取值的集合。
在证明和推理中,我们需要确定函数的定义域
和值域,确保推导的严谨性。
2. 函数的奇偶性:当函数满足f(-x) = f(x)时,我们称其为偶函数;当函数满足f(-x) = -f(x)时,我们称其为奇函数。
在证明中,
奇偶性的性质可用于简化推理过程。
3. 函数的单调性:函数的单调性分为递增和递减两种。
当函数
满足f(x1) ≤ f(x2)时,称其为递增函数;当函数满足f(x1) ≥ f(x2)时,称其为递减函数。
单调性在证明中常常用于确定函数的极值点和
临界点。
二、函数的证明方法
1. 直接证明法:直接证明法是一种常用的证明方法,通过列出
已知条件和证明结论,逐步演绎证明的正确性。
在函数的证明中,我们需要清晰地列出假设条件、使用数学定理和性质,并逐步推
导出目标结论。
2. 反证法:反证法是一种常用的证明方法,通过假设结论不成立,推导出矛盾的结果,从而证明原始结论的正确性。
在函数的
证明中,我们可以运用反证法来证明函数的特定性质,如存在唯
一性等。
3. 数学归纳法:数学归纳法是一种常用的证明方法,用于证明
满足自然数集上的性质。
在函数的证明中,数学归纳法可以用于
证明递推关系、等式等。
三、函数的推理方法
1. 等式推理:等式推理是函数推理中最基本的方法,通过运用
等式的性质,将一个等式变换为另一个等式,以推导出目标结果。
2. 不等式推理:不等式推理是函数推理中常用的方法,通过运
用不等式的性质,确定函数的变化范围,推导出满足条件的自变
量范围。
3. 极限推理:极限推理是函数推理中重要的方法,通过运用极
限的定义和性质,确定函数在某一点处的性质,并推导出相应的
结论。
四、实例分析
为了更好地理解函数的证明与推理,我们以一个实例进行分析。
假设我们需要证明函数f(x) = x^2在定义域为实数集时是递增函数。
首先,我们可以尝试使用直接证明法。
假设x1 < x2,且x1和
x2都属于实数集。
我们需要证明f(x1) ≤ f(x2)。
根据函数的定义,我们可以得到f(x) = x^2。
代入x1和x2,有
f(x1) = x1^2,f(x2) = x2^2。
由于x1 < x2,根据实数的乘法性质,我们可以得到x1^2 ≤
x2^2。
因此,我们得出了f(x1) ≤ f(x2)的结论,即函数f(x) = x^2是递
增函数。
通过这个实例,我们可以看到函数的证明与推理需要运用定义、定理和性质,并通过逐步演绎和推导,得出相应的结论。
五、总结
本课件介绍了函数的证明与推理的基本概念和方法。
我们从函数的定义与特性开始,回顾了函数的基本知识。
然后,我们介绍了函数的证明方法,包括直接证明法、反证法和数学归纳法。
同时,我们也介绍了函数的推理方法,包括等式推理、不等式推理和极限推理。
最后,通过一个实例分析,我们展示了函数的证明与推理的具体应用。
函数的证明与推理是数学中的重要技能,帮助我们深入理解函数的性质,并在解决数学问题时做出准确的推断和推理。
通过学习和掌握函数的证明与推理方法,我们可以提升数学思维和分析问题的能力,为进一步学习和研究奠定基础。
希望本课件对您的学习有所帮助,谢谢阅读!。