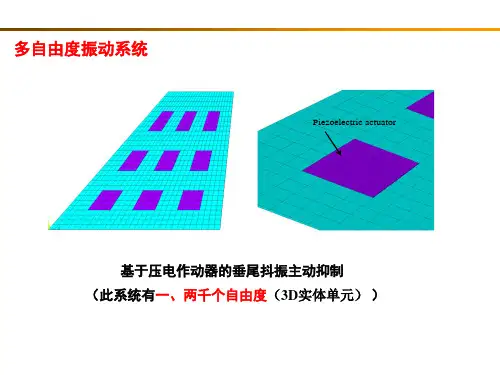
多自由度系统

多自由度系统振动的研究1.建立系统的数学模型：多自由度系统的数学模型通常可以通过运动微分方程来描述，这些微分方程可以由拉格朗日方程或哈密顿方程获得。

建立系统的数学模型是研究多自由度系统的第一步，它能够定量描述系统的振动特性。

2.振动模态分析：振动模态是指各种独立振动模式对应的特征值及特征向量。

在多自由度系统中，有多个振动模态，每个振动模态都有对应的特征值和特征向量，它们描述了系统在不同振动模态下的振动特性。

振动模态分析可以帮助我们理解系统的振动特性、模式和共振现象，并为系统的设计和优化提供依据。

3.模态叠加方法：模态叠加方法是一种常用的分析多自由度系统振动响应的方法。

该方法将系统的初始条件和外力激励在模态基下展开，通过将各模态响应相加，得到系统的总体振动响应。

模态叠加方法可以简化计算，使得问题的求解更加方便，应用广泛。

4.模态分析与结构动力学：多自由度系统的模态分析与结构动力学密切相关。

结构动力学是研究结构体受外力激励下的振动响应的学科，它通常涉及到多自由度系统的模态分析、频率响应和时域分析等。

模态分析为结构动力学提供了基础，通过分析结构的振动模态，可以预测结构在不同激励下的振动响应。

5.数值模拟与实验验证：在研究多自由度系统的振动过程中，可以借助于数值模拟和实验验证相结合的方法。

数值模拟可以通过有限元、边界元或半经验法等方法，对系统的振动响应进行计算和预测。

实验验证可以通过振动台试验或实验模态分析等方式，对系统的振动特性进行实测，从而验证数值模拟的准确性。

总之，研究多自由度系统振动是一个复杂而又重要的课题。

通过建立数学模型、进行振动模态分析、应用模态叠加方法以及进行数值模拟和实验验证等手段，可以更深入地了解多自由度系统的振动特性，为实际工程问题的求解和优化提供科学依据。

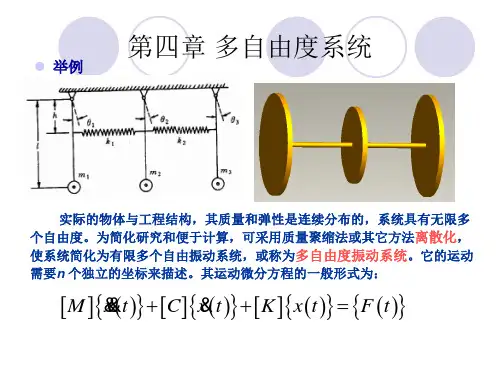
4．1 多自由度系统的数学描述一、用柔度系数法和刚度系数法表示的运动方程下面以图4-1的系统为例说明多自由度系统的柔度系数及柔度矩阵。

柔度矩阵所谓柔度是指单位外“力”所引起的系统的“位移”。

具体地说，系统第个坐标上作用的单位力在第个坐标上所引起的位移就定义为柔度系数r。

如在图4-1系统中，设在质量上沿方向作用一单位力，系统相应于它产生的位移为按柔度系数的定义，就有同理，一个自由度的系统一共有个独立坐标，对应于每个单位力就有个柔度系数；总共有个单位力，故系统总共有个柔度系数（。

它们组成一个柔度矩阵（4-1）假设在系统的各个坐标上分别作用有力，则由叠加原理，系统的各个位移可表示为写成矩阵表式，有（4-2）其中与分别代表位移列阵和力列阵：也就是说，系统的位移列阵就等于系统的柔度矩阵与力列阵的乘积。

方程（4-2）称为位移方程。

应注意，本书中的“力”与“位移”都是指广义的，“力”可以是力，也可以是力偶；而“位移”可以是线位移，也可以是角位移，等等。

下面举例说明怎样求系统的柔度矩阵。

例4-1 设有集中质量与以及长为与的无重刚杆构成的复合摆，如图4-2所示，假定摆在其铅垂稳定平衡位置附近作微振动。

取质量与的水平位置与作为坐标，求系统的柔度矩阵。

解：先仅在上作用一单位水平力。

由静力平衡条件可得：因而有再仅在上作用一单位水平力。

由静力平衡条件有：考虑到可得故系统的柔度矩阵为刚度矩阵所谓刚度是指产生单位“位移”所需的各个外加“力”。

具体地说使系统仅仅在第个坐标上产生单位位移，就需要在各个坐标方向分别加上适当的力，而在第个坐标上所需加的外力，就定义为刚度系数。

一个自由度系统有个独立的坐标，对应着个单位位移，而每个单位位移又对应着个刚度系数；所以系统总共有个刚度系数，它们组成一个刚度矩阵（4-3）例如在图4-1系统中，设有这时，弹簧与没有变形，而弹簧伸长了单位长度，作用于质量上的弹簧力为（向右为正），而作用于质量上的弹簧力为-（向左为负）。

第5章多自由度系统的数值计算方法在工程实践中，我们经常会遇到多自由度系统（Multiple Degree of Freedom，简称MDOF）的问题，例如振动台、建筑结构等。

这些系统通常由多个自由度所组成，因此其运动方程会比单自由度系统更加复杂。

因此，我们需要使用数值计算方法来求解这些系统。

在本章中，我们将介绍两种常见的数值计算方法，包括直接积分法和模态叠加法。

一、直接积分法直接积分法，也称为时步法或时间积分法，是一种常用的求解MDOF系统的数值计算方法。

它的基本原理是将多自由度系统的运动方程转换为一组一阶常微分方程。

然后，利用数值积分方法，如欧拉法、Runge-Kutta法等，对这组常微分方程进行求解，得到系统的运动响应。

直接积分法的主要步骤如下：1.确定系统的运动方程：根据多自由度系统的动力学原理，可以得到系统的运动方程。

一般来说，这个方程是非线性方程，通常需要进行线性化处理。

2.将运动方程转化为一阶常微分方程组：将系统的运动方程进行适当的变换，将其转化为一组一阶常微分方程。

这样，就可以使用数值积分方法对其进行求解。

3. 选择数值积分方法：选择适合系统的数值积分方法，例如欧拉法、Runge-Kutta法等。

这些方法的基本思想是将微分方程转化为差分方程，通过迭代来逼近准确解。

4.进行数值计算：根据选择的数值积分方法，进行迭代计算，得到系统的运动响应。

尽管直接积分法是一种广泛应用的数值计算方法，但也存在一些问题。

例如，随着自由度的增加，计算量会大大增加。

此外，由于数值积分方法的局限性，可能会出现数值不稳定、数值发散等问题。

二、模态叠加法模态叠加法是求解MDOF系统的另一种常用数值计算方法。

该方法基于模态分析的思想，将MDOF系统的运动方程转化为一组无耦合的一自由度系统的运动方程。

然后，按照模态响应的叠加原理，将各个模态的响应相加，得到系统的总体响应。

模态叠加法的主要步骤如下：1.确定系统的模态参数：通过模态分析方法，可以得到系统的模态参数，包括模态频率、振型等。

多自由度体系的动力响应分析多自由度体系的动力响应分析是研究多个质点或刚体组成的系统在外界作用下的运动规律和响应特性的一项重要课题。

多自由度体系是指由多个相对独立的质点或刚体组成的系统，其中每个质点或刚体都可以在三个方向上自由运动，因此系统具有多个自由度。

多自由度体系的动力学方程可由牛顿第二定律推导得出，即∑F = ma，其中∑F 表示作用在系统中各质点上的合力，m 表示质点的质量，a 表示质点的加速度。

根据每个质点的运动规律，可以得到系统在不同自由度上的运动方程。

为了简化多自由度体系动力学方程的求解，常采用试解法和模态分析法。

试解法是假设质点的位置和速度可以用特定的试解函数表示，然后将试解函数代入动力学方程中，从而得到未知系数的值。

模态分析法则是将系统的自由度进行正交分解，得到一组特征向量和特征值，将试解函数表示为特征向量的线性组合。

通过求解特征值问题，可以得到系统的固有频率和模态振型，从而分析系统的动力响应。

自由振动是指在没有外界作用的情况下，多自由度体系在初始时刻给定的初始条件下的运动。

通过求解系统的运动方程，可以得到质点位置随时间的变化规律。

自由振动的特点是系统在固有频率上做周期性的振动，同时各自由度之间存在能量的转移和耦合。

强迫振动是指在外界施加周期性的激励力下，多自由度体系的运动。

外界激励力的形式可以是单频、多频或宽频带等。

通过求解系统的运动方程，可以得到系统在激励力作用下的动力响应。

强迫振动的特点是系统在激励频率附近发生共振现象，振幅会显著增大。

阻尼振动是指当多自由度体系存在阻尼力的情况下的振动。

阻尼力可以分为线性阻尼和非线性阻尼两种情况。

线性阻尼是指阻尼力与质点速度成正比的情况，非线性阻尼是指阻尼力与质点速度的高阶项有关的情况。

根据阻尼力的形式，可以得到不同类型的阻尼振动方程。

求解阻尼振动方程，可以得到系统的动力响应，包括振动幅值、相位和能量耗散等。

多自由度体系的动力响应分析在工程领域有广泛的应用。

多自由度系统最小作用量原理多自由度系统是指系统中包含多个可以独立运动的自由度，其中每个自由度可以由一个或多个坐标变量描述。

最小作用量原理是描述这些自由度的运动方程的一种原理，它基于拉格朗日力学和变分原理。

本文将从介绍多自由度系统开始，解释什么是自由度以及如何描述这些自由度的运动方程。

接下来，将详细介绍最小作用量原理的概念，涉及到拉格朗日函数、虚位移以及作用量的定义。

最后，将对最小作用量原理的应用进行讨论，并简要介绍其中的一些应用案例。

一、多自由度系统的介绍多自由度系统是指系统中包含多个可以独立运动的自由度。

自由度是描述物体在空间中能够自由运动的方向或程度的数量。

对于一个质点而言，它只有三个自由度，分别对应三个坐标轴上的位置变量。

而对于包含多个质点或刚体的系统，则存在多个自由度。

多自由度系统的运动可以由多个坐标变量来描述。

这些坐标变量通常被称为广义坐标。

广义坐标是一组与自由度相对应的独立变量，通过它们可以完整地描述系统的状态。

广义坐标的选取可以有多种方式，但一定要能够完整地表示所有的自由度。

多自由度系统的运动可以通过拉格朗日力学来描述。

拉格朗日力学是一种通过最小作用量原理导出系统运动方程的方法。

最小作用量原理指出，在一个系统的运动中，作用量取极小值。

作用量是指在一个过程中，系统在每个瞬时状态下的能量之和。

对于多自由度系统，作用量可以由广义坐标的函数表示。

二、最小作用量原理的概念最小作用量原理是建立在拉格朗日力学和变分原理的基础上的。

拉格朗日函数是描述系统动力学的一个重要概念，它是广义坐标和它们的导数的函数。

拉格朗日函数可以通过系统的动能和势能来构建，通常表示为L(q, q')，其中q表示广义坐标，q'表示广义坐标的导数。

为了导出系统的运动方程，我们需要考虑广义坐标的变化。

变分原理指出，在系统运动过程中，广义坐标可以发生无穷微小的变化，这些变化被称为虚位移。

虚位移可以写作δq。

最小作用量原理的核心思想是，系统的真实运动路径使作用量取极小值。