当前位置：文档之家 › 等腰三角形的判定

等腰三角形的判定

  • 格式：ppt
  • 大小：805.50 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

等腰三角形的判定

等腰三角形的判定

lpt48hkn
为“藏传佛教的八大神山之首。”我们到达梅里雪山的时候是在早晨，结束了几天的地下生活，到了梅里雪山脚下，阳光刺的我睁不 开眼睛，过了一会终于适应了。阳光明媚，山上的雪被阳光照得熠熠生辉，极蓝与极白相交辉映，看着这样的风景好像心也被洗干净 了，空气里都满是雪的味道。我现在终于体会到什么是壮观，在大自然的面前人类是多么的渺小。巍峨的雪山直插云霄，真是雾笼云 遮缥缈中，浑然浩气贯苍穹。山神说拉着我的手，我啊了一声，有点不好意思，脸红的发烫，感觉都红到耳根了。山神看着我说： “想什么呢，拉着我，我们飞上去，这样会节省不少时间。”这是要是有一条地缝，不管多小，我都要挤进去。可等了半天，山神也 没什么动静，他的手依旧如此冰凉。我以为他还在酝酿，只见他眉头紧皱，我说怎么了，我们怎么还在这里。山神说：“在这里，我 居然不能使用法术，我的法术好像被什么禁锢了一样，没法使出来。”我心想这座山这么厉害，居然连山神的法力都被禁锢了，看来， 我们凶多吉少了，真是壮士一去兮不复返啊。我说：“这样啊，那我们还是走吧，万一在这里挂掉了，我还好，你可怎么办啊，多不 划算啊。”我边说边往回走。山神说：“来都来了，再说了，怕什么，这是神山，不会有什么妖怪的。看来，我们只有爬上去了”。 这里有十三座峰，主峰卡瓦格博峰海拔高达6740米，看着主峰，我咽了口唾沫，心想这次不死也要退层皮了。我们修整了一会开始爬 山，我们就一直走，也无心欣赏身边的风景了，山很陡峭，有几次险些摔倒下去，我们一直提心吊胆地走了一天，到傍晚的时候终于 到达了雪线，我们又继续往前走，天也渐渐暗下来了，想想开始露出来，星星离我们很近，温度逐渐降低，风越来越大，尽管穿着很 厚很厚地冬衣，依然感觉很冷，只要一张口，风吹着雪就直往喉咙里灌，山神怕我摔倒后爬不起来，就一直拉着我走，满眼的白色， 一直看着白色突然头一阵眩晕，一不小心就跌了个狗**。山神连忙把我扶起来。山神还是一身玄色衣服，他无论在什么样的恶劣条件 都是这样，丝毫不受影响。走到后来就是他拖着我走了，他怕我失去意识，就一直不停的跟我说话。我们又走了一夜，到第二天中午， 我们来到了一个山洼里，这的山洼很奇怪，它很宽很大，周围长满了野花和野草，还能看到很多蝴蝶，一条清澈的小溪从旁边流过， 这里这的是一处世外桃源啊，想不到大山之中还能有这样的地方不受风雪的侵扰。山神的眼睛很尖，一下就看到了被草掩埋的相机， 拿起来一看，这是尼康FM3A上面的金属机身已经长锈了，相机更新速度很快，现在已经停产了，我们也不能评这个就判断时间，万一 他是胶卷相机的忠实用户呢，这也说不定，随后我们又找到

9 等腰三角形的性质判定

9 等腰三角形的性质判定

已知：如图，在△ABC中，∠B=∠C
求证： AB=AC
A
B
D
C
例：如图，∠EAC是△ABC的外角， AD平分∠EAC，且AD∥BC. 求证：AB=AC
E
A
D
B
C
如果AB=AC，AD∥BC，那么 AD平分∠EAC吗？
E
A
D
B

C
练 习
证明：等边三角形的每个角都 等于 60 0 证明：线段垂直平分线上的点 到线段两端距离相等。
B
C
例：如图1，等边△ABC中，D是AB上的一动点， 以CD为一边向上作等边△EDC，连AE，
求证：AE∥BC
（2）如图2，将（1）中等边△ABC改为以BC为 底边的等腰三角形所作△EDC改为相似于△ABC， 请问：是否仍有AE∥BC？证明你的结论。
A D B E D C A
E
B
图1
C
图2
如图，点C为线段AB上的一点△ACM，△CBN 是等边三角形线段AN、CM相交于点E，线段 BM、CN相交于点F。（1）求证：AN=BM （2）△CEF是等边三角形
900 ， （3）将△ACM绕点C逆时针方向旋转
在图2中补出符合条件的的图形，并判断（1） （2）两题的结论是否仍然成立，证明你的结论。
M N E A C F B M A C N
B
等腰三角形的性质和判断
定理：等腰三角形的两个底角相等 （“等边对等角”）
你能用几种方法证明？
定理：等腰三角形的两个底角相等 （“等边对等角”）
已知：如图，在△ABC中，AB=AC 求证：∠B=∠C
A
B
D
C
定理：等腰三角形的顶角 平分线、 底边上的中线和高是同一条直线。 （三线合一）

等腰三角形的判定讲义

等腰三角形的判定讲义

等腰三角形的判定-讲义等腰三角形一、知识梳理定义：有两条边相等的三角形是等腰三角形。

相等的两条边叫做腰，另一条边叫做底。

两腰所夹的角叫做顶角；腰与底边的夹角叫做底角。

1.等腰三角形的性质性质1：等腰三角形的两个底角相等（简称“等边对等角”）．性质2：等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合（简称“三线合一”）．2.等腰三角形的性质的作用证明同一个三角形中的两角相等.是证明角相等的一个重要依据．用来证明线段相等，角相等，垂直关系等．3.等腰三角形是轴对称图形4.等腰三角形底边上的高（顶角平分线或底边上的中线）所在直线是它的对称轴，通常情况只有一条对称轴．二、等腰三角形的判定1.如图，在△ABC中，AB=AC，∠A=36°，BD，CE分别为∠ABC，∠ACB的角平分线，则图中等腰三角形共有________个2.下列能断定 △ ABC为等腰三角形的是（）A．∠A=30°，∠B=60°B．∠A=50°，∠B=80°C．AB=AC=2，BC=4D．AB=3，BC=7，周长为103.在平面直角坐标系中，O是坐标原点，点A（3，2），点P（m，0）（m＜6），若△POA是等腰三角形，则m可取的值最多有（ ）A．2个 B．3个 C．4个 D．5个4.如图，在△ABC中，AB=AC，∠A=120，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为_______5.若△ABC的三边a，b，c满足（a-b）（b-c）（c-a）=0，那么 △ABC的形状是___________6.如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论正确的有_____________①△ BDF和 △ CEF都是等腰三角形；② DE=BD+CE；③△ ADE的周长等于AB与AC的和；④ BF=CF．7.如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB=AC，AC=AD，有四个结论：①AC⊥BD；②BC=DC；③△ABC≌△ADC；④△ABD是等边三角形．其中正确的是_____________8.如图，△ABC是等边三角形，延长BC到E，使CE＝BC．点D是边AC的中点，连接ED并延长ED交AB于F，求证：（1）EF⊥AB；（2）DE＝2DF9.如图，BO，CO分别平分∠ABC，∠ACD，OD//AB，OE//AC，若AC=6，AB=7，BC=8则△DOE的周长是_______10.如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于点E，D垂足，连接EC求∠ECD的度数；若CE=5求BC长 .11.已知△ABC是等腰直角三角形，∠ABC=90°，AB=BC，D是AC的中点，F是AD上一点，连接BF，过点C作CE⊥BF于点E.求证：AF=BG.12.已知：如图，A B=AC，点D是的中点，A B平分∠DAE，AE⊥BE（1）求证：A D=AE；（2）若B E//AC，试判断△ABC的形状，并说明理由.13.在平面直角坐标系xOy中，直线y=2x+b与x轴交于点（1，0），与一次函数y=x+3的图象相交于点A．（1）求b的值，并直接在图中画出这两个一次函数的图象（不写画图过程）；（2）求点A的坐标；（3）若P是x轴的正半轴上一点，且满足是等腰三角形，直接写出点P的坐标．14.如图，在平面直角坐标系中xoy中，∠AOB=90°，AB=CD=a，OD=OA=b，点B的坐标为（c，0），且|a-13|+（b-12）2=-（c-5）2.（1）求点C的坐标；（2）求证；DC⊥AB（3）在x轴上找一点P，使△PDC是以DC为腰的等腰三角形，请直接写出点P的坐标.三、直角三角形斜边中线定理如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。

等腰三角形的性质与判定

等腰三角形的性质与判定

等腰三角形的性质与判定等腰三角形是初中数学中的一个重要概念，它具有一些独特的性质和判定方法。

在本文中，我们将探讨等腰三角形的性质和判定，并通过几个例子加深理解。

首先，我们来了解等腰三角形的定义。

等腰三角形是指具有两条边相等的三角形。

根据这个定义，我们可以得出等腰三角形的第一个性质：等腰三角形的底角（底边对应的角）是相等的。

这是因为等腰三角形的两条边相等，所以它们对应的角也必须相等。

接下来，我们来探讨等腰三角形的第二个性质：等腰三角形的高线（从顶点到底边的垂直线段）是对称轴。

这个性质可以通过几何推理来证明。

假设我们有一个等腰三角形ABC，其中AB = AC。

如果我们从顶点A向底边BC引一条垂直线段AD，我们可以证明BD = CD。

这是因为在等腰三角形中，高线将底边等分，所以BD = CD。

这也意味着高线AD是底边BC的中垂线，而中垂线是对称轴。

除了这些基本性质外，等腰三角形还有一些判定方法。

首先，我们可以通过边长判定法来判断一个三角形是否为等腰三角形。

如果一个三角形的两条边相等，那么它就是等腰三角形。

其次，我们可以通过角度判定法来判断一个三角形是否为等腰三角形。

如果一个三角形的两个角相等，那么它就是等腰三角形。

这两种判定方法可以互相验证，帮助我们确定一个三角形是否为等腰三角形。

让我们通过一个例子来加深对等腰三角形性质和判定的理解。

假设我们有一个三角形DEF，其中DE = DF。

我们可以通过边长判定法得出这个三角形是等腰三角形。

接下来，我们可以通过角度判定法验证这个结论。

如果我们发现角D和角E相等，那么我们可以确定这个三角形是等腰三角形。

通过计算角度，我们可以发现角D和角E的度数相等，所以我们可以得出结论：三角形DEF是等腰三角形。

在实际生活中，等腰三角形的性质和判定方法也有一些应用。

例如，在建筑设计中，等腰三角形的对称性可以用于设计对称美观的建筑物。

在工程测量中，等腰三角形的判定方法可以帮助工程师确定一个三角形的性质，从而更好地进行测量和计算。

等腰三角形的判定

等腰三角形的判定

等腰三角形的判定判定等腰三角形的基本方法：一是从定义入手，证明两条边相等；二是从角入手，证明一个三角形的两个角相等。

在实际的阶梯中，有些常用的技巧就是构造等腰三角形从而利用等腰三角形的性质为解题服务，常用的构造方法有1、“角平分线+平行线”构造等腰三角形。

2、“角平分线+垂线”构造等腰三角形。

3、用“三角形中角的2倍关系”构造等腰三角形。

例题求解【例题1】如图，在△ABC中，AB=7，AC=11，点M是BC的中点，AD是∠BAC的平分线，MF//AD。

则FC的长为________。

【例题2】如图，已知直角△ABC中，∠A=30°，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有_____个。

【例题3】如图，△ABC中，AD⊥BC于点D，∠B=2∠C，求证：AB+BD=CD.【例题4】两个全等的含有30°、60°的三角板ADE和三角板ABC，如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．【例题5】如图，△ABC中，∠C=90°，∠CAD=30°，AC=BC=AD，求证：CD=BD。

学力训练基础夯实1、如图，∠ABC=50°，AD垂直平分线段BC于点D，∠ABC的角平分线BE交AD 于E，连接EC；则∠AEC等于（2、如图，△ABC中，AB=AC，∠ABC=36°，D，E是BC上的两点，且∠B A D=∠D A E=∠EAC，则图中等腰三角形的个数是（）3、如图，△ABC中，AD平分∠BAC，AB+BD=AC,则∠B：∠C的值是_______。

4、已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是________．5、如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的中垂线，E、N在BC上，则∠EAN=（）6、如图所示，在△ABC中，∠B=2∠C，则AC与2AB之间的关系式______。

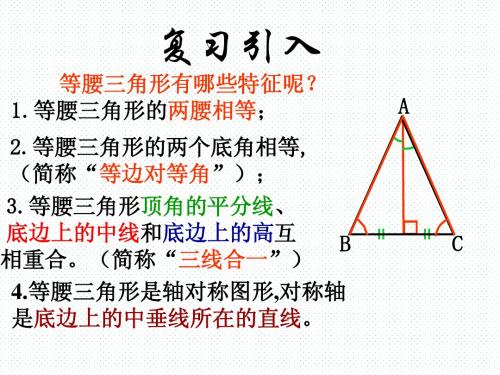
等腰三角形的判定

等腰三角形的判定
O
A
B
O 已知：如图，在ΔOAB中， ∠A=∠B，求证:OA=OB. A C 证明：过O点作OC⊥AB，垂足为C. 在ΔOAC和ΔOBC中， ∠A=∠B ∠OCA= ∠OCB=90° OC=OC ∴ ΔOAC ≌ΔOBC ∴ OA=OB
B
等腰三角形的判定：
如果一个三角形中有两个角 相等,那么这两个角所对的边也相 等.(等角对等边)
A 有两边 相等的 三角形 是等腰 三角形。 C
1.两边相等。
2.等边对等角, 3. 三线合一。 4.是轴对称图形.
2.等角对等边,
思考题1 如图,线段AB的端点B在直线 l 上(AB与直线 l 不 垂直)，请在直线 l 上另找一点C,使ΔABC为等腰 三角形，这样的点能找几个？你能说出它们的画 法吗？ A
理由．
B
30
O
60
O
A D
C
心动
不如行动
A
如图:△ABC中AB=AC,∠B=∠C， BD=CE，说明∠1=∠2的理由，
B D
1
2
E ∠1=∠2
C
方法一:
BD=CE ∠B=∠C AB=AC
△ABD≌ △ACE
AD=AE
方法二: △ABD≌ △ACE
方法三:
BE=CD ∠B=∠C AB=AC
∠ADB＝∠AEC
A C
如图，标杆AB高5m， 为了将它固定，需要由 它的中点C向地面上与点 B距离相等的D，E两点 拉两条绳子，使得点D， B，E在一条直线上。量 得DE=4m，绳子CD和 CE要多长？
E
D
B
例1：一次数学实践活动的内容是测量河宽，如图，即 测量A,B之间的距离.同学们想出了许多方法,其中小聪 的方法是：从点Ａ出发,沿着与直线AB成60°角的AC方 向前进至C，在C处测得∠C＝30°.量出AC的长，它就是 河宽（即A,B之间的距离）．这个方法正确吗？请说明

等腰三角形的判定定理


A
图中有哪些角相等?
∠ B= ∠ C.
B
在三角形中等边C中， ∠ B= ∠ C， AB=AC 成立吗？
探索思考
1，作一个三角形，有两个角 相等，这两个角所对的边是否
相等？
A
分析: 在ΔABC中, ∠B=∠C作∠BAC
的平分线交BC于D, 则
12
∠ 1=∠2, 又∠B=∠C, 由三角形
内角和的性质得∠ADB=∠ADC, B D C
沿直线
AD折叠∠ADB=∠ADC ,
∠1= ∠2, 所以射线DB与射线DC重合, 射线AB与射线
AC重合, 从而点B与点C重合, 因此AB=AC
等腰三角形有以下的判定方法:
如果一个三角形有两个角相等，那么这个三角形是等腰三 角形.
简单地说；在同一个三角形中，
2.4等腰三角形的判定定理
复习引入
等腰三角形有哪些特征呢？ 1.等腰三角形的两腰相等.
2.等腰三角形的两个底角相等, （简称“等边对等角”）.
3.等腰三角形顶角的平分线、 底边上的中线和底边上的高互 B 相重合.（简称“三线合一”）
4.等腰三角形是轴对称图形,对称轴 是底边的中垂线.
A C
1.如图:ΔABC中,已知AB=AC,
A
D
B
C
练习5
2.如图，在等腰△ABC 中，AB=AC，两底角的 平分线BE和CD相交于 点O，那么△OBC是什 D 么三角形？ 为什么？
B
A
E O
C
小结
名称 图 形
等
腰
三
角
A
形
概念
性质与边角关系
判定
有两边 相等的 三角形 是等腰 三角形

等腰三角形性质与判定

等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。

2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。

3.等腰三角形的两底角的平分线相等，两条腰上的中线相等，两条腰上的高相等。

4.等腰三角形底边上的垂直平分线到两条腰的距离相等。

5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。

6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。

7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。

8.等腰三角形中腰的平方等于高的平方加底的一半的平方。

9.等腰三角形中腰大于高。

10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)。

等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。

2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。

3.三线合一逆定理：顶角的平分线，底边上的中分线，底边上的高，其中任意两个重合的三角形是等腰三角形。

等腰三角形的判定

等腰三角形的判定至少有两边相等的三角形叫做等腰三角形。

等腰三角形中，相等的两条边称为这个三角形的腰，另一边叫做底边。

等腰三角形判定定理是：在一个三角形中，如果两个角相等，那么这两个角所对的边也相等。

判定方法有：等腰三角形的认定等腰三角形的认定方法1、在一个三角形中，如果一个角的平分线与该角对边上的中线重合，那么这个三角形是等腰三角形。

2、在一个三角形中，如果一个角的平分线与该角对边上的高重合，那么这个三角形就是等腰三角形。

3、在一个三角形中，如果一条边上的中线与该边上的高重合，那么这个三角形是等腰三角形。

4、存有两条角平分线或中线、或低成正比的三角形就是等腰三角形。

判定的方式：定义法：在同一三角形中，存有两条边成正比的三角形就是等腰三角形。

判定定理：在同一三角形中，如果两个角相等，那么这两个角所对的边也相等（简称：等角对等边）。

除了以上两种基本方法以外，除了如下认定的方式：1、在一个三角形中，如果一个角的平分线与该角对边上的中线重合，那么这个三角形是等腰三角形，且该角为顶角。

2、在一个三角形中，如果一个角的平分线与该角对边上的高重合，那么这个三角形就是等腰三角形，且该角为顶角。

3、在一个三角形中，如果一条边上的中线与该边上的高重合，那么这个三角形是等腰三角形，且该边为底边。

似乎，以上三条定理就是“三线合一”的逆定理。

4、有两条角平分线（或中线，或高）相等的三角形是等腰三角形。

等腰三角形的分类：1、等腰直角三角形：有一个角是直角的等腰三角形，叫做等腰直角三角形。

它是一种特殊的三角形，具有所有等腰三角形的性质，同时又具有所有直角三角形的性质。

2、等边三角形：就是三边都成正比的等腰三角形。

性质：1、等腰三角形的两个底角度数成正比（缩写成“等边对等角”）。

2、等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合（简写成“等腰三角形三线合一”）。

3、等腰三角形的两底角的平分线成正比（两条腰上的中线成正比，两条腰上的高成正比）。

等腰三角形的判定和性质

2 等腰三角形 第1课时 等腰三角形的判定和性质
一、等腰三角形的性质 1.定理:等腰三角形的两个底角相等.简述为: 等边对等角 . 2.定理:等腰三角形顶角的平分线、底边上的 中线 、底边上的 高
互相
重合.这一结论通常简述为“三线合一”. 3.等腰三角形两底角的平分线 相等 ;两条腰上的中线 相等 的高 相等 .
;两条腰上
【知识拓展】 等腰三角形底边上任意一点到两腰的距离和等于一腰上的高. 二、等腰三角形的判定
有两个角相等的三角形是等腰三角形.简述为: 等角对等边 .
知识点一 等腰三角形的性质
【例1】如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E. 求证:∠CBE= ∠BAD.
证 明 : 法 一 因 为 AB=AC,AD 是 BC 边 上 的 中 线 , 所 以 AD⊥BC,∠BAD=∠CAD, 所 以 ∠ CAD+ ∠C=90°. 因 为 BE⊥AC, 所 以 ∠ CBE+∠C=90°. 所 以 ∠ CBE=∠CAD, 所 以 ∠CBE=∠BAD. 法二 因为AB=AC,所以∠ABC=∠C.又因为AD是BC边上的中线,所以AD⊥BC,所以 ∠BAD+ ∠ABC=90°.因为BE⊥AC,所以∠CBE+∠C=90°,所以∠CBE=∠BAD.
解:(1)①②;①③.
(2)请选择(1)中的一种情形,写出证明过程.
解:(2)选①②证明如下:在△BOE和△COD中, 因为∠EBO=∠DCO,∠EOB=∠DOC,BE=CD, 所以△BOE≌△COD,所以BO=CO, 所以∠OBC=∠OCB, 所以∠EBO+∠OBC=∠DCO+∠OCB, 即∠ABC=∠ACB,所以AB=AC, 即△ABC是等腰三角形. 选①③证明如下: 在△BOC中,因为OB=OC,所以∠OBC=∠OCB. 因为∠EBO=∠DCO, 所以∠EBO+∠OBC=∠DCO+∠OCB, 即∠ABC=∠ACB,所以AB=AC,即△ABC是等腰三角形.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品课件
细心观察，探索性质
等边三角形的判定定理1：
三个角都相等的三角形是等边三角形．
符号语言：
C
在△ABC 中，
∵ ∠A=∠B =∠C ，
∴ △ABC 是等边三角形．
A
B
精品课件
已知：在等腰△ABC中，AB=AC， ∠A=60°(或者∠B=60°）
求证：AB=AC=BC A
60°
60°
B
C
你又可以得到什么？
D
∴AB=AC (等角对等边)
1
3
∵ AD平分∠BAC
2
4
∴ ∠BAD=∠CAD
B
C
∴ AD在等腰△ABC 的顶角的角平分线上
∴ AD⊥BC (等腰三角形的“三线合一”)
小试牛刀
例：如图,上午10 时，一条船从A处出发以20海里
每小时的速度向正北航行，中午12时到达B处，从A
、B望灯塔C，测得∠NAC=40°∠NBC=80°求从B处
不考虑风浪因素）？
O
A
B
精品课件
探 究 新 知
做一做
● 操作一 画△ABC.使∠B＝∠C＝30°
● 操作二 量一量，线段AB与AC的长度。
你发现了什么结论？其他同学的结果与你
的相同吗？
怎样用数
AB=AC
学推理进 行证明呢？
精品课件
如果一个三角形有两个角相等,那么这两 个角所对的边也相等
已知：如图,在ΔABC中，∠B=∠C1= ∠2
∴ ∠B ＝ ∠C(等量代换)
∴AB=AC (等角对等边）
精品课件
已知：在△ABC中，∠A=∠B=∠C 求证：AB=AC=BC A
B
C
从以上讲解我们可以得到什么结论？
精品课件
推论1：三个角都相等的三角形是等边三角形 。
这是由判定定理推导出的一个定理， 即判定一个三角形是等边三角形的一 种方法。
A
求证：AB=AC
证明: 作∠BAC的平分线AD ∴∠1=∠2
12
在△BAD和△CAD中 ∠B=∠C(已知)
∵ ∠1=∠2(已证)
AD=AD (公共边)
B
D
C
你还有其
∴ △BAD ≌ △CAD (A.A.S.)
他证法吗
∴ AB= AC (全等三角形的对应边相等) ?
精品课件
已知：如图,在ΔABC中，∠B=∠C。
求证：AB=AC
A
证明：作AD⊥BC，垂足为D
∴ ∠ADB= ∠ADC=900
在 △BAD和△CAD中，
□
∵
∠B=∠C(已知) ∠ADB= ∠ADC(已证)
B
□ D
AD=AD(公共边） C ∴ △BAD≌△CAD（A.A.S.）
∴AB=AC（全等三角形的对应边
相等）
精品课件
注意：在同一个 等腰三角形的判定定理： 三角形中应用哟！
C
分析：要证AB=AC，就要证∠B=∠C，而已知 有∠1= ∠2，只要找出∠B、 ∠C与∠1、 ∠2的关系就可以了。
精品课件
已知：如图，∠CAE是△ABC的外角， ∠1=∠2， AD∥BC。求证：AB=AC
E
1
A2
解：∵AD∥BC
∴∠1= ∠B (两直线平行，同位角相等
D）
∠ 2 ＝ ∠C(两直线平行，内错角相等
A
证明： ∵ DE∥BC ∴
∠1=∠B,∠2=∠C ∵ ∠1=∠2
∴AD=AE(等角对等边) ∠B=∠C(等量代换) ∴AB=AC (等角对等
边) ∴AB-AD=AC-AE
精品课件
D1 2 E
B
C
已知：如图，AD∥BC，BD平分∠ABC
求证：AB=AD
A
D
证明： ∵ AD∥BC
∴ ∠ADB=∠DBC
精品课件
推论2：有一个角等于60°的等腰三 角形是等边三角形。
这是由判定定理推导出的又一个定理， 即判定一个三角形是等边三角形的另 外一种方法。
精品课件
等边三角形的判定定理2： 有一个角为60°的等腰三角形是等边三角形．
C
符号语言：
在△ABC 中，
∵ BC =AC，∠A =60°
∴ △ABC 是等边三角形． A
若AB≠AC，其他 条件不变，图中 还有等腰三角形
∵ EF=EO+FO
吗？(1)中结论还
∴EF＝BE+FC
成立吗？
精品课件
求证：如果三角形一个外角的平分线平行于三 角形的一边，那么这个三角形是等腰三角形。
E
1
A2
已知：如图，∠CAE是△ABC的 D 外角， ∠1=∠2，AD∥BC
求证：AB=AC
B
B
精品课件
△ABC 是等边三角形，DE∥BC, 分别交AB，AC 于点D，E．求证：△ADE 是等边三角形.
A
证明：∵ △ABC 是等边三角形，
如果一个三角形有两个角相等，那么 这两个角所对的边也相等
(简写成“等角对等边”)。
A
几何语言：
∵∠B =∠C (已知)
∴ AB=AC(等角对等边) B
C
精品课件
等腰三角形的性质与判定有区别吗?
性质是:1.等边
等角
2.三线合一
判定是:等角
等边
精品课件
已知:如图,DE∥BC,∠1=∠2.求证:BD=CE.
一、复习引入 等腰三角形 定义： 有两边相等的三角形是等腰三角形。 性质1： 等腰三角形的两个底角相等。
(等边对等角)
性质2： 等腰三角形的底边上的中线和高线、 顶角平分线互相重合。 (三线合一)
精品课件
问题情境 ：
如图，位于海上A、B两处的两艘救生船接到O处 遇险船只的报警，当时测得∠A=∠B。如果这两艘救生 船以同样的速度同时出发，能不能同时赶到出事地点（
∵ BD平分∠ABC B
C
∴ ∠ABD=∠DBC
∴ ∠ABD=∠ADB(等量代换)
∴ AB=AD(等角对等边)
∴AB=AC (等角对等边)
精品课件
已知：在△ABC 中，∠1=∠3,∠2=∠4，AD
平分∠BAC。求证：AD⊥BC
A
证明： ∵ ∠1=∠3,∠2=∠4
∴ ∠1+∠2=∠3+∠4
即 ∠ABC=∠ACB
O.过O作EF∥BC交AB于E，交AC于F.请你写出图中所
有等腰三角形，并探究EF、BE、FC之间的关系
AA
解：EF=BE+CF 理由如下：
∵ BO、CO分别平分∠ABC、∠ACB ∴∠2＝∠ABO ，∠3＝∠ACO ∵ EF∥BC
E E
B B
O FF
1 4C
2
3C
∴∠1＝∠2 ，∠3＝∠4
∴∠1＝∠ABO ∠4＝∠ACO ∴BE＝EO FC=FO (等角对等边)
到灯塔C的距离 解：∵ ∠NAC=40°∠NBC=80°
∴∠C=∠NBC-∠NAC
C
80° N 北
=80°-40° = 40°
B 40°
∴ ∠C = ∠A ∴ BA=BC（等角对等边） ∵AB=20×（12-10）=40（海里）
A
∴BC=40 （海里）
答：B处到达灯塔C的距离为40海里。
精品课件
在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点