浓度问题应用题及答案

浓度问题六年级应用题一、知识点回顾1. 浓度的定义溶液中溶质的质量（或体积）与溶液的质量（或体积）之比叫做溶液的浓度。

通常用百分数表示。

浓度公式，溶液的质量（或体积）=溶质的质量（或体积） + 溶剂的质量（或体积）。

2. 常见的浓度问题类型及解题思路稀释问题：在稀释过程中，溶质的质量（或体积）不变。

例如，把高浓度的溶液加水变成低浓度的溶液。

浓缩问题：在浓缩过程中，溶质的质量（或体积）不变。

例如，蒸发溶剂使溶液浓度升高。

混合问题：将两种或多种不同浓度的溶液混合，混合前后溶质的总质量（或总体积）不变。

二、典型例题及解析（一）稀释问题1. 题目现有浓度为公式的盐水公式克，要把它稀释成浓度为公式的盐水，需要加水多少克？2. 解析根据浓度公式求出原来盐水中盐的质量。

原来盐水浓度为公式，盐水质量为公式克，那么盐的质量公式盐水质量公式浓度，即公式克。

稀释后盐水的浓度变为公式，但是盐的质量不变还是公式克。

设稀释后盐水的质量为公式克，根据浓度公式可得公式，即公式，解得公式克。

原来盐水质量是公式克，现在稀释后盐水质量是公式克，所以需要加的水的质量公式稀释后盐水质量原来盐水质量，即公式克。

（二）浓缩问题1. 题目有公式克浓度为公式的盐水，要蒸发掉多少克水才能使盐水的浓度变为公式？2. 解析先求出原来盐水中盐的质量，盐的质量公式盐水质量公式浓度，即公式克。

设蒸发掉公式克水后盐水浓度变为公式。

此时盐水的质量为公式克，根据浓度公式可得公式，即公式。

展开式子得公式。

移项得公式，即公式。

解得公式克，所以要蒸发掉公式克水。

（三）混合问题1. 题目浓度为公式的酒精溶液公式克与浓度为公式的酒精溶液公式克混合，混合后酒精溶液的浓度是多少？2. 解析先分别求出两种溶液中酒精的质量。

浓度为公式的公式克酒精溶液中酒精的质量为公式克。

浓度为公式的公式克酒精溶液中酒精的质量为公式克。

混合后酒精的总质量为公式克。

混合后溶液的总质量为公式克。

则混合后酒精溶液的浓度公式。

分数问题—专题练习《浓度问题》一．选择题1．（2018秋•抚宁区期末）含糖量是10%的糖水200克，糖不变，要使含糖量降低到8%，需要加水() A．4克B．50克C．250克【分析】抓住糖的重量不变，先根据一个数乘分数的意义，用“20010%20⨯=”计算出糖水中糖的质量；后来糖水的8%是20克，根据已知一个数的几分之几是多少，用除法求出后来糖水的质量，根据“后来糖水的质量-原来糖水的质量=加入水的质量”解答即可．【解答】解：20010%8%200⨯÷-=-250200=（克)50答：需要加水50克．故选：B．2．（2019•益阳模拟）在浓度为16%的40千克盐水中，蒸发()水后可将浓度提高到20%．A．8千克B．9千克C．16千克D．4千克【分析】用40千克减去浓度是20%的盐水的盐水的重量，就是应蒸发掉水的重量．因盐的重量不变，含盐⨯千克，含盐20%的盐水的重量就是20%的盐水中的盐等于含盐16%的盐水中的盐，既(4016%)⨯÷千克，据此解答．(4016%20%)-⨯÷，【解答】解：404016%20%=-，40328=（千克）；答：蒸发8千克水后可将浓度提高到20%．故选：A．3．（2019•益阳模拟）现在有果汁含量为40%的饮料600ml，要把它变成果汁含量为25%的饮料，需要加水()ml．A．400 B．240 C．360 D．100【分析】根据一个数乘分数的意义，先用“60040%⨯”计算出600ml 果汁饮料中含有果汁的重量是240ml ，进而根据“果汁含量不变”，得出后来果汁含量为25%的饮料的果汁含量是240ml ；根据已知一个数的几分之几是多少，求这个数，用除法计算出后来果汁饮料的重量，继而用“后来果汁饮料的重量-原来果汁饮料的重量”解答即可．【解答】解：果汁含量：60040%240()ml ⨯=，后来果汁饮料的重量：24025%960()ml ÷=，需要加水：960600360()ml -=，答：需要加水360ml ．故选：C ．4．（2019•益阳模拟）把20克的盐放入100克水，盐与水的最简整数比是( )A ．1:6B ．1:5C ．20:100【分析】要求“盐与水的比是多少”，必须知道盐和水的质量，此题已经给出，所以用盐的质量：水的质量即可．【解答】解：20:1001:5=．故选：B ．5．（2018•长沙）浓度为70%的酒精溶液500克与浓度为50%的酒精溶液300克，混合后所得到的酒精溶液的浓度是( )A ．62.5%B ．60%C ．61.5%D ．57%【分析】根据“溶质质量=溶液质量⨯浓度”分别求出每种浓度溶液中纯酒精的质量，再用两种溶液中酒精的质量之和除以两种溶液的质量．【解答】解：(50070%30050%)(500300)⨯+⨯÷+(350150)800=+÷500800=÷62.5%=答：混合后所得到的酒精溶液的浓度是62.5%．故选：A ．6．有甲、乙、丙三种盐水，按甲与乙的数量之比为2:1混合得到浓度为13%的盐水，按甲与乙的数量之比为1:2混合得到浓度为14%的盐水，如果按甲、乙、丙的数量之比为1:1:3混合得到的盐水浓度为10.2%，那么丙的浓度为( )A ．7%B ．8%C ．9%D ．7.5%【分析】根据：“按甲与乙的数量之比为2:1混合”，“按甲与乙的数量之比1:2混合”，“按甲、乙、丙的数量之比1:1:3混合”．从上面的条件中我们发现，只要使前两次操作得到的12%的盐水与14%的盐水重量相等，就可以使12%的盐水与14%的盐水混合，得到浓度为(12%14%)213%+÷=的盐水，这种盐水里的甲和乙的数量比为1:1．现在我们要用这样的盐水与盐水丙按2:3混合，得到浓度为10.2%的盐水，13%10.2% 2.8%-=，这样2份的13%的盐水就多了5.6%，这5.6%正好补全了丙盐水与10.2%的盐水的差距，5.6%3 1.87%÷≈，10.2% 1.87%8.33%-=，所以丙盐水的浓度为8.33%．【解答】解：(12%14%)213%+÷=；(13%10.2%)2 5.6%-⨯=；10.2% 5.6%3-÷10.2% 1.87%≈-8.33%=答：丙盐水的浓度约为8.33%．故选：B ．二．填空题7．（2019•广东）杯中有浓度为36%的盐水，倒入一定量的水后，盐水的浓度降低到30%，若要稀释到浓度为24%，则再加入的水是上次所加水的 1.5 倍．【分析】这杯浓度为36%的盐水，假设盐水重100克，盐就是10036%36⨯=克，倒入一定量的水后，盐水的浓度降低到30%，由于盐的重量不变，所以此时盐水的重量是盐的重量除以浓度，是3630%120÷=克，那么加入水的重量就是12010020-=克，若要稀释到浓度为24%，那么加入水的重量应是3624%12030÷-=克，用除法求出再加入的水是上次所加的几倍即可．【解答】解：假设盐水重100克，盐的重量：10036%36⨯=（克）÷=（克）浓度30%时盐水的重量：3630%120-=（克）加入水的重量：12010020÷=（克）浓度24%时盐水的重量：3624%150-=（克）第二次加入水的重量：15012030÷=3020 1.5答：再加入的水是上次所加水的1.5倍．故答案为：1.5．8．（2019春•沈阳月考）1000千克葡萄含水率为96.5%，一周后含水率降为96%，这些葡萄的质量减少了125千克．【分析】含水率下降，这一过程中纯葡萄的质量不变，先把原来葡萄的总质量看成单位“1”，用原来葡萄的质量乘96.5%，求出原来水的质量，进而求出纯葡萄的质量；再把后来葡萄的总质量看成单位“1”，它-就是纯葡萄的质量，再根据分数除法的意义求出后来葡萄的总质量，用原来的总质量减去现在的(196%)的总质量，就是减少的质量．-⨯【解答】解：1000100096.5%=-1000965=（克)35÷-35(196%)=÷354%=（千克）875-=（千克）1000875125答：这些葡萄的质量减少了125千克．故答案为：125．9．（2019•郑州模拟）浓度为70%和40%的酒各一种，现在要用这两种酒配制含酒精60%的酒300克，需要浓度70%的酒200克，浓度40%的酒克．-克，根据一种浓度是70%，另一种浓度为40%，【分析】设取70%的酒精x克，则取40%的酒精(300)x现在要配制成浓度为60%的洒精300克，可列方程求解．【解答】解：设取70%的酒精x 克，则取40%的酒精(300)x -克，则由题意得：70%(300)40%30060%x x +-=⨯，0.71200.4180x x +-=0.360x =200x =所以300300200100x -=-=（克）．答：需70%的酒精200克，40%的酒精100克．故答案为：200；100．10．（2019•长沙）130克含盐5%的盐水，与含盐9%的盐水混合，配成含盐6.4%的盐水，这样配成的6.4%的盐水有 200 克．【分析】设含盐9%的盐水为x 克，则配成的盐水中含盐是(1305%9%)x ⨯+，盐水是(130)x +克，再根据含盐率是6.4%，列出方程求出x 的值，再加上130克即可．【解答】解：设含盐9%的盐水为x 克，根据题意可得方程：1305%9%(130) 6.4%x x ⨯+=+⨯，6.50.098.320.064x x +=+，0.026 1.82x =，70x =，13070200+=（克)，答：这样的盐水有200克．故答案为：200．11．（2019•长沙）100克15%浓度的盐水中，放进了盐8克，为使溶液的浓度为20%，那么，还得再加进水 7 克．【分析】加入8克后，溶液共有10015823⨯+=克盐，达到20%后的溶液总质量为2320%115÷=（克)．加入8克盐后总质量为108克，故应该再加水1151087-=（克）．【解答】解：(10015%8)20%(1008)⨯+÷-+，2320%108=÷-，115108=-，7=（克)；答：还得再加水7克．12．（2019•上街区）有糖水若干，加入一定量的水后，含糖率降低到3%，第二次又加入同样多的水后，含糖率降低到2%，第三次再加入同样多的水，这时糖水的含糖率是 1.5 %．【分析】糖水第一次加入水后含糖率降低到了3%，第二次在加入同样多的水后含糖率降到了2%，这里面不变的量是糖的质量没有变，我们可以设加入了X 水，原来有的水看成1，那么第一次加入水后糖的含量是(1)3%X +⨯第二次加入水后糖的含量是(1)2%X X ++⨯，这样我们就可以求出加入的水是X 是多少，(1)3%(1)2%X X X +⨯=++⨯可以求出1X =，第三次加入同样多的水后糖的含量是3(11)3%(113) 1.5%200+⨯÷+⨯==故第三次加入同样多的水后这时糖水的含糖量是1.5%．【解答】解：设加入水x 杯，第一次加入x 杯水后，糖水的含糖百分比变为3%--即含糖(1)3%x +⨯第二次又加入同样多的水，糖水的含糖百分变比为2%--即含糖(1)2%x x ++⨯得(1)3%(1)2%x x x +⨯=++⨯1x = 第三次再加入同样多的水，糖水的含糖3(11)3%(113) 1.5%200+⨯÷+⨯==故第三次加入同样多的水后的糖水的含糖量是1.5%答：第三次加入同样多的水后，这时糖水的含糖量是1.5%．13．（2018•长沙）小高想要配制浓度为35%的盐水，目前他有浓度为20%的盐水280克．需要再加入浓度为40%的盐水 840 克．【分析】原盐水从20%到35%，浓度提高了35%20%15%-=，加入的盐水从40%到35%，浓度减少了40%35%5%-=，原盐水共280克，所以加入的盐水应该为：28015%5%840⨯÷=克．【解答】解：280(35%20%)(40%35%)⨯-÷-28015%5%=⨯÷840=（克)答：需要再加入浓度为40%的盐水 840克．故答案为：840．14．（2018•南京）两个相同的瓶子装满酒精溶液，一个瓶中酒精与水的体积之比是3:1，而另一个瓶中酒精与水的体积之比是4:1．若把两瓶酒精溶液混合，混合液中酒精与水的体积之比是 31:9 ．【分析】根据题意，把两瓶酒精溶液混合后，酒精与水的体积之和没变，把两个酒精瓶的容积分别看作一个单位，求出酒精和水各占酒精瓶容积的几分之几，然后再求混合液中酒精和水的体积之比是多少． 【解答】解：将一个酒精瓶容积看成一个单位，则在一个瓶中，酒精占33314=+，水占11134=+； 而在另一个瓶中，同样，酒精占44415=+，水占11415=+；于是在混合液中，酒精和水的体积之比是：3411():()4545++，319:2020=，31:9=．答：混合液中酒精和水的体积之比是31:9．故答案为：31:9．15．（2018•南昌）桶中有些浓度为40%的某种盐水，当加入5千克水后，浓度降低到30%，再加入 8 千克盐，可使盐水的浓度提高到50%．【分析】设原来盐水为x 千克，则原溶液中盐的质量40%x ⨯，加入水后盐的质量不变但溶液质量增加，所以可求出原来盐水的质量；同样加入盐后盐的质量40%x y =⨯+，溶液质量5x Y =++，从而依据浓度公式列式求解．【解答】解：设原来有盐水x 克，40%(5)30%x x ÷+=，0.40.3(5)x x =⨯+，0.40.3 1.5x x =+，0.1 1.5x =，15x =；设再加入y 克盐，(1540%)(155)50%y y ⨯+÷++=，60.5(20)y y +=⨯+，60.5100.50.5y y y y +-=+-，60.56106y +-=-，0.50.540.5y ÷=÷，8y =，答：再加入8千克盐，可使盐水的浓度提高到50%．故答案为：8．16．（2018•长沙）一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，盐水的含盐百分比变为12%；第三次再加入同样多的水，盐水的食盐百分比将变为 10 %．【分析】由题意可知：第一次加入一定量的水后，盐水含盐量的百分比变为15%，第二次又加入同样多的水，盐水含盐量的百分比变为12%，那么由含盐量不变即可列式计算．【解答】解：第一次加入一定量的水后，盐水含盐量的百分比变为15%，第二次又加入同样多的水，盐水含盐量的百分比变为12%，那么由含盐量不变，第二次又加入同样多的水后，含盐量=第一次加入一定量的水后的盐水12%⨯+第二次所加入的水的重量12%⨯=第一次加入一定量的水后的盐水15%⨯，所以第一次加入一定量的水后的盐水：所加入一定量的水12%:15%12%4:1=-=；所以未加水时的盐水：每次所加入一定量的水41:13:1=-=；所以第三次加入同样多的水，盐水含盐量的百分比将变为(31)15%10%3111+⨯=+++．故答案为：10．17．（2017•长沙）将100g 浓度为20%的食盐溶液与200g 浓度为25%的食盐溶液混合，再将混合溶液蒸发100g 水，得到的溶液浓度为 35% ．【分析】根据溶液混合前后，溶质的质量不变，溶质质量=溶液质量⨯溶质的质量分数，溶质质量分数100%=⨯溶质质量溶液质量，进行分析解答．【解答】解：溶液混合前后，溶质的质量不变，100g 浓度为20%的食盐溶液与200g 浓度为25%的食盐溶液混合，再将混合溶液蒸发100g 水，最后所得溶液的溶质质量分数是10020%20025%100%100200100⨯+⨯⨯+-2050100%200+=⨯ 70100%200ϖ=⨯35%=；答：得到的溶液浓度为35%．故答案为：35%．三．判断题18．（2008秋•疏勒县期末）把10克糖放入到90克水中，这时糖水的含糖率为10%． √ ．（判断对错） 【分析】应正确理解含糖率，即糖的重量占糖水重量的百分之几，计算方法为：100%⨯糖的重量糖水的重量；进行解答继而进行判断； 【解答】解：10100%10%1090⨯=+； 故答案为：√．19．将a 克盐完全溶解在一些清水中，含盐率正好是10%，若接着在这些盐水中又溶解a 克盐后，含盐率就达到20%． 错误 ．（判断对错）【分析】根据盐的重量是a 克，含盐率=盐的重量÷盐和水的总重量100%⨯，即可求出盐水重量10%10a a ÷=克，再加入a 克盐后，盐是2a 克，盐水的重量为1011a a a +=，再根据含盐率=盐的重量÷盐和水的总重量100%⨯，据此解答．【解答】解：盐水重量10%10a a ÷=（克），含盐率：()(10)18.18%a a a a +÷+≈，所以若接着在这些盐水中又溶解a 克后，含盐率就达到20%，是错误的． 故答案为：错误．四．应用题20．（2019秋•温县期末）某酒厂有48︒的白酒（含酒精48%)125千克，现在要把它勾兑成50︒的白酒，需要添加酒精多少千克？【分析】根据题意，加入酒精，把含酒精48%的白酒变成含酒精50%的白酒，那么水的质量不变，先把原来白酒的总质量看成单位“1”，用原来白酒的总质量乘(148%)-，求出水的质量，再把后来白酒的总质量看成单位“1”，它的(150%)-就是水的质量，然后根据分数除法的意义求出后来白酒的总质量，再减去原来白酒的总质量，就是加入酒精的质量．【解答】解：125(148%)⨯-12552%=⨯65=（千克）65(150%)÷-6550%=÷130=（千克）1301255-=（千克）答：需要添加酒精5千克．21．（2019春•黄冈期末）在质量为200kg ，浓度为50%的硫酸溶液中，再加入多少千克浓度为5%的硫酸溶液，就可以配制浓度为25%的硫酸溶液？【分析】先求出200千克浓度为50%的硫酸中的含硫酸的量，设出加入x 千克浓度为5%的硫酸溶液，就可以配制浓度为25%的硫酸溶液．则加入的溶液中含硫酸的量为5%x 千克，而配制成的溶液中含硫酸的量为25%(200)x ⨯+千克，由此根据硫酸的含量不变列出方程，解答即可．【解答】解：设加入x 千克浓度为5%的硫酸溶液，就可以配制浓度为25%的硫酸溶液．根据硫酸的含量不变列出方程：20050%5%25%(200)x x ⨯+⨯=+1000.050.2550x x +=+0.250x =250x =答：加入250千克浓度为5%的硫酸溶液，就可以配制浓度为25%的硫酸溶液．22．（2019•郑州）浓度10%的酒精溶液50克、浓度15%的酒精溶液50克与浓度12%的酒精溶液100克混合，混合后的酒精溶液浓度是多少？【分析】先计算各种酒精溶液中酒精的含量，以及酒精溶液的总质量，然后根据浓度问题公式：浓度=溶质÷溶液100%⨯，代入公式计算混合后酒精溶液的浓度即可．【解答】解：(5010%5015%10012%)(5050100)100%⨯+⨯+⨯÷++⨯24.5200100%=÷⨯12.25%=答：混合后的酒精溶液的浓度为12.25%．23．（2019•泉州模拟）甲、乙两种酒各含酒精72%和48%，要配制含酒精64%的酒3600克，应当从这两种酒精中各取多少克？【分析】根据题意，设需要甲酒x 克，则需要乙酒(3600)x -克，根据酒精的含量不变，有：甲种酒中酒精含量+乙种酒中酒精含量64%=的酒的酒精含量，列方程求解即可．【解答】解：设需要甲酒x 克，则需要乙酒(3600)x -克，72%48%(3600)360064%x x +⨯-=⨯0.720.4836000.4836000.64x x +⨯-=⨯0.243600(0.640.48)x =⨯-0.2436000.16x =⨯2400x =360024001200-=（克)答：需要甲种酒2400克，乙种酒1200克．24．（2018秋•高碑店市期末）一杯糖水90克，糖和水的质量比是1:8，如果再加入10克糖，这时糖占糖水的百分之几？【分析】含糖率是指糖的质量占糖水总质量的百分之几；先用原来糖水的总质量乘118+，求出原来糖的质量，再把原来糖的质量加上放入糖的质量，求出后来糖的总质量，然后用原来糖水的总质量加上加入的糖的质量，即可求出后来糖水的总质量，然后用后来糖的总质量除以后来糖水的总质量，再乘100%即可．【解答】解：1901018⨯=+（克）(1010)(9010)100%+÷+⨯20100100%=÷⨯20%=答：这时糖占糖水的是20%．25．（2018春•辛集市期末）把含盐为5%的40kg盐水，调制成含盐率为2%的盐水．先把你的调制方法写出来，再计算说明．【分析】含盐量由5%降到2%，可以运用加水的方法，先把原来盐水的总质量看成单位“1”，用原来盐水的质量乘5%，求出不变的盐的质量，再用盐的质量除以后来的含盐率，即可求出后来盐水的总质量，进而求出加水的质量．【解答】解：405%2⨯=（千克）22%100÷=（千克）1004060-=（千克）答：可以加入60千克的水．26．（2018•东莞市模拟）含糖6%的糖水40克，要配制成含糖20%的糖水，应加糖多少克？【分析】浓度为6%的糖水40克，含水的质量为40(16%)37.6⨯-=（克)，加糖的过程中，水的质量不变，浓度为20%的糖水重量是37.6(120%)÷-，计算出结果，再减去40克即可．【解答】解：水的质量为：40(16%)37.6⨯-=（千克）；新的糖水的质量为：37.6(120%)47÷-=（千克）；所以需要加糖：47407-=（千克）．答：需要加糖7千克．27．（2019春•湖南月考）浓度为20%、18%、16%的三种盐水，混合后得到50克18.8%的盐水．如果18%的盐水比16%的盐水多15克，问：每种盐水各多少克？【分析】根据题干，设16%盐水有x 克，则18%的盐水有(15)x +克，又因为混合后共50克，则20%的盐水有：50(15)352x x x --+=-克，然后用各自的质量乘各自的浓度，得出各自的盐的重量，再相加，即等于50克浓度为18.8%的盐水中盐的重量，据此列方程为：16%18%(15)20%(352)5018.8%x x x ⨯+⨯++⨯-=⨯，然后解方程即可得出答案．【解答】解：设16%的盐水质量为x 克，则18%的盐水质量为(15)x +克，20%的盐水质量为50(15)(352)x x x --+=-克．则根据题意可得：16%18%(15)20%(352)5018.8%x x x ⨯+⨯++⨯-=⨯0.160.18 2.770.49.4x x x +++-=9.70.069.4x -=0.060.3x =5x =51520+=（克)5052025--=（克)答：16%、18%20%的三种盐水分别有5克、20克、25克．4.16%、18%、20%的盐水各5克、20克、25克28．（2019春•湖北月考）甲种酒精4千克，乙种酒精6千克，混合成的酒精含纯酒精62%；如果甲种酒精和乙种酒精一样多，那么混合成的酒精含纯酒精61%．甲种酒精中含酒精的百分数是多少？【分析】甲种酒精4升，乙种酒精6升，混成的酒精含纯酒精62%，即乙种酒精比甲多了2升，其中纯酒精共(46)62% 6.2+⨯=（升）；如果用4升甲与4升乙混合，那么混合成的酒精含纯酒精61%，其中纯酒精共(44)61% 4.88+⨯=（升）；也即2升乙酒精中含纯酒精6.2 4.88 1.32-=（升），所以乙种酒精中含纯酒精的百分数为：(1.322)100%66%÷⨯=，甲为：61%266%56%⨯-=，据此解答即可．【解答】解：(46)62% 6.2+⨯=（升）；如果用4升甲与4升乙混合，那么混合成的酒精含纯酒精61%，其中纯酒精共(44)61% 4.88+⨯=（升）； 2升乙酒精中含纯酒精6.2 4.88 1.32-=（升），乙种酒精中含纯酒精的百分数为：(1.322)100%66%÷⨯=，甲为：61%266%56%⨯-=，答：甲种酒精中含纯酒精56%，乙种酒精中含纯酒精66%．29．（2019•长沙）有甲、乙、丙三瓶溶液，甲比乙浓度高6%，乙的浓度是丙的4倍．如果把乙溶液倒入甲中，就会使甲溶液的浓度比原来下降2.4%：如果把丙溶液倒入乙溶液中，就会使乙溶液的浓度比原来下降2.25%；如果把甲、丙两瓶溶液混合，则混合液的浓度正好等于乙溶液的浓度．请问：甲、乙、丙三瓶溶液的质量比是多少？它们的浓度分别是多少？【分析】设乙溶液的浓度为%x ，甲乙丙三种溶液的质量分别为：A ，B ，C ，甲乙混合后浓度为：6 2.4% 3.6x x +-=+，乙丙混合后浓度为： 2.25x -，甲丙混合后浓度为x ，据此列方程解答即可．【解答】解：设乙溶液的浓度为%x ，甲乙丙三种溶液的质量分别为：A ，B ，C ，则有：甲的浓度为(6)x +，丙的浓度为4x，依题意有如下关系：(6) 3.6Bx A x x A B +⨯+=++23A B =①4 2.25x Bx C x B C +⨯=-+32.25 2.254Cx B C =-② (6)4xA x C x A C ⨯++⨯=+364CxA =③ 将③式代入①式，得12CxB =④ 将④式代入②式，得4x =，即乙溶液的浓度为4%，则甲溶液的浓度为10%，丙溶液的浓度为1%．将4x =代入②式，得3C B =，因此::3:2:6A B C =．答：甲、乙、丙三瓶溶液的质量比是3:2:6，甲的浓度为：10%，乙的浓度为：4%，丙的浓度为1%．30．（2018•东莞市）将100克浓度为40%的盐水和150克浓度为10%的盐水混合，要配制成浓度为30%的盐水，需再加浓度为40%的盐水多少克？【分析】根据已有盐水的浓度和质量，算出第一次混合后的浓度，即(10040%15010%)(100150)22%⨯+⨯÷+=，然后根据“十字相乘法”解答即可．【解答】解：(10040%15010%)(100150)⨯+⨯÷+55250=÷22%=(40%30%):(30%22%)--10%:8%=5:4=(100150)54+÷⨯25054=÷⨯200=（克）答：需再加浓度为40%的盐水200克．五．解答题31．（2019•长沙）把浓度为20%的盐水倒掉5千克后，再往剩下的盐水中加入浓度为60%的盐水30千克，得到浓度为35%的盐水．原来浓度为20%的盐水有多少千克？【分析】设原来浓度为20%的盐水有x 千克，倒掉5千克后，变为(5)x -千克，再依据浓度公式，含盐率=盐的重量盐水的重量，由此列式求解．【解答】解：设原来浓度为20%的盐水有x 千克，(5)20%3060%(530)35%x x -⨯+⨯=-+⨯20%11835%8.75x x -+=+15%8.25x =55x =，答：原来浓度为20%的盐水有55千克．32．（2019•宁波）有盐水若干升，加入一定量的水后，盐水浓度降到3%，又加入同样多的水后，盐水浓度又降到2%，再加入同样多的水，此时浓度是多少？未加入水时盐水浓度是多少？【分析】浓度为3%，也就是盐3份水97份，共100份，浓度下降为2%，原来3份盐就成了2%，因此可求出加入了多少份水．第二次加水后盐和水总共32%150÷=（份)，第二次加水15010050-=（份)，即每次加水50份，然后根据浓度公式就可以求出：第三次加水后的浓度和不加水前的浓度，据此解答．【解答】解：浓度为3%，也就是盐3份水97份，共100份，浓度下降为2%，原来3份盐就成了2%． 第二次加水后盐和水总共：32%150÷=（份)，第二次加水15010050-=（份)，即每次加水50份， 所以，第三次加水后浓度3 1.5%15050=+， 不加水前的浓度为36%10050=-；答：第三次加水后浓度为1.5%，未加水前浓度为6%．33．（2019•广东模拟）有A 杯浓度为25%的盐水和B 杯浓度为40%的盐水混合在一起后，得到的盐水浓度为30%，A 杯盐水重量与B 杯盐水之比是 2 : ．【分析】我们要以先设A 杯水中有盐水为x ，则有盐的含量就是25%x 即是14x ，设B 杯中有盐水为主y ，则盐的含量就是30%y ，即310y ；两杯混合后和到的盐水重量是，x y +，而这时的盐含量是，30%()x y +；即3()10x y +．我们可以利用两杯盐的分别所占的比比例和，与混合后的盐所占的比例，我们可以建立等式：123()4510x y x y +=+，我们可以利用等式性质，得到:2:1x y =．故A 杯盐水重量与B 杯之比是2:1．【解答】解：设有A 杯中有盐水X ，则盐有14x ，B 杯中有盐水y ，则有盐25y ，故有方程我们可以建立等式：123()4510x y x y +=+1232020()204510x y x y ⨯+⨯=+⨯5866x y x y +=+8665y y x x -=-2y x =2y x x x ÷=÷21y x =2212y x ÷=÷12y x = 故:2:1x y =答：A 杯盐水和B 杯盐水重量之比是2:1．34．（2019•长沙）甲种酒精纯酒精含量为72%，乙种酒精纯酒精含量为58%，混合后纯酒精含量为62%，如果每种酒精取的数量比原来多15升，混合后纯酒精含量为63.25%，问第一次混合时，甲乙两种酒精各取了多少升．【分析】先求出第一次取出的甲、乙酒精的重量比，再求出第二次取出的甲乙的重量比，然后设第一次混合时，甲种酒精应取2x 升，乙种酒精应取5x 升，根据第二次取出的甲乙的重量比列出方程求解，即可解决问题．【解答】解：第一次取出的甲、乙酒精的重量比为：(62%58%):(72%62%)2:5--=；第二次取出的甲、乙酒精的重量比为：(63.25%58%):(72%63.25%)3:5--=；设第一次混合时，甲种酒精应取2x 升，乙种酒精应取5x 升，则(215):(515)3:5x x ++=，3(515)5(215)0x x +-+=，154510750x x +--=，57545x =-，530x=，x=；6x=⨯=，2261255630x=⨯=．答：第一次混合时，甲种酒精应取12升、乙种酒精取30升．35．（2017•长沙）浓度为70%的酒精溶液500克与浓度为50%的酒精溶液300克，混合后所得到的酒精溶液的浓度是多少？【分析】根据“溶质质量=溶液质量⨯浓度”分别求出每种浓度溶液中纯酒精的质量，再用两种溶液中酒精的质量之和除以两种溶液的质量．⨯+⨯÷+【解答】解：(50070%30050%)(500300)=+÷(350150)800=÷800800=62.5%答：混合后所得到的酒精溶液的浓度是62.5%．36．（2019•长沙）一种35%的新农药，如果稀释成浓度为1.75%时，治虫最有效，用多少千克浓度为35%的农药加多少千克的水，才能配成1.75%的农药800千克？【分析】先要明白：药+水=药水，药水的浓度是：药占药水的百分之几．要配制浓度为1.75%的新农药⨯，即14千克．因为是用35%的药水配制而成，800千克，则800千克药水中所含的药即可求出(800 1.75%)÷．最后用800千克减去40千克即为所加水的重因此，所需要浓度为35%的药水数就可求出，即：1435%量，分步列式解答即可．⨯÷【解答】解：药的含量：(800 1.75%)35%=÷1435%=（千克）40-=（千克）．水的重量：80040760答：需要浓度为35%的新农药40千克，需加水760千克．37．（2018•娄底模拟）要调配两种不同浓度的桔子汁，甲容器中有纯桔汁8升，乙容器中有水7升，如果要使甲容器中纯桔汁含量为80%，乙容器中纯桔汁含量为40%，则最后甲、乙容器各有多少升？【分析】现有的甲容器中，桔子汁为100%，要稀释到80%，得：880%10÷=（升），要从乙中到入甲中1082-=（升）的水，则乙中还剩725-=（升）的水； 要使乙中含有40%的桔子汁，则要从甲往乙到入桔子汁，设要从甲中倒入乙x 升，则：80%(5)40%x x ÷+=，解之得5x =，则甲中有80%的桔子汁：8255+-=（升），乙中有40%的桔子汁：72510-+=（升）．【解答】解：现有的甲容器中，桔子汁为100%，要稀释到80%，得：880%10÷=（升），要从乙中到入甲中1082-=（升）的水，则乙中还剩725-=（升）的水；要使乙中含有40%的桔子汁，则要从甲往乙到入桔子汁，设要从甲中倒入乙x 升，80%(5)40%x x ÷+=80%40%2x x =+40%2x =5x =，则甲中有80%的桔子汁：825+-105=-5=（升），乙中有40%的桔子汁：725-+55=+10=（升），答：最后甲容器有5升、乙容器有10升．38．（2018•重庆模拟）甲容器中有浓度为20%的盐水400克，乙容器中有浓度为10%的盐水600克，分别从甲和乙中取相同重量的盐水，把从甲容器中取出的盐水倒入乙容器，把乙容器中取出的盐水倒入甲容器，现在甲、乙容器中盐水浓度相同，则甲、乙容器中各取出多少克盐水倒入另一个容器？【分析】设甲、乙容器中各取出x 克盐水倒入另一个容器，然后根据现在甲、乙容器中盐水浓度相同，列方程为：(400)20%10%(600)10%20%400600x x x x -⨯+-⨯+=，解之得240x =，据此解答即可．【解答】解：设甲、乙容器中各取出x 克盐水倒入另一个容器，由题意得：(400)20%10%(600)10%20%400600x x x x -⨯+-⨯+=600(800.1)400(600.1)x x -=+4804800.62400.4x x --=+4800.60.62400.40.6x x x x -+=++480240x =+240480x +=240240480240x +-=-240x =答：甲、乙容器中各取出240克盐水倒入另一个容器．39．（2018•长沙）用含盐5%的盐水和含盐8%的盐水混合成含盐6%的盐水600克，问这两种盐水应各取多少克？【分析】本题含有两个未知数，可用方程解答，设需要浓度为5%的盐水x 克，则需要浓度为8%的盐水(600)x -克，由此用乘法分别表示出其中所含的食盐多少克，这两部分食盐相加就等于浓度为6%的盐水600克所含的食盐量，据此关系列方程解答即可．【解答】解：设需要浓度为5%的盐水x 克，则需要浓度为8%的盐水(600)x -克，5%8%(600)6006%x x +⨯-=⨯5%488%36x x +-=3%12x =400x =600400200-=（克），答：需要浓度为5%的盐水400克，需要浓度为8%的盐水200克．。

小学数学应用题-浓度问题1、【来源】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%．如果每种酒精都多取20克，混合后纯酒精的含量变为45%．求甲、乙两种酒精原有多少克？2、【来源】2016年吉林长春南关区东北师范大学附属中学实验小学小升初（明珠校区）第19题6分2019~2020学年浙江杭州上城区天长小学六年级上学期期中第33题5分2019~2020学年11月广东深圳福田区深圳外国语学校东海附属小学六年级上学期周测A卷第9题2019年浙江杭州上城区杭州市崇文实验学校六年级上学期单元测试《分数乘法、百分数》第20题有浓度为3.2%的食盐水500克，为了把它变成浓度是8%的食盐水，需要使它蒸发掉多少克的水？3、【来源】2018~2019学年四川成都双流县四川师范大学附属圣菲小学六年级下学期期末第18题8分2019~2020学年10月四川成都龙泉驿区四川师范大学附属上东小学六年级上学期周测D卷第27题6分2019年重庆沙坪坝区重庆市第一中学小升初入学真卷第21题5分陕西西安小升初专题39第28题5分2019年陕西咸阳秦都区西北工业大学启迪中学小升初入学真卷第22题7分甲种酒含纯酒精40%，乙种酒含纯酒精36%，丙种酒含纯酒精35%．将这三种酒混在一起得到含纯酒精38.5%的酒11千克．已知乙种酒比丙种酒多3千克，那么甲种酒有多少千克？4、【来源】甲、乙两瓶盐水，甲瓶盐水的浓度是乙瓶盐水浓度的3倍．将100克甲瓶盐水与300克乙瓶盐水混合后得到浓度为15%的新盐水，那么甲瓶盐水的浓度是多少？5、【来源】2015~2016学年北京六年级上学期期末用含盐5%的盐水和含盐8%的盐水及100克水混合成含盐6%的盐水700克，那么，这两种盐水应各取多少克来混合？6、【来源】2018~2019学年四川成都温江区成都实验外国语附属小学六年级下学期开学考试第28题5分2018年四川成都郫都区成都市外国语学校小升初第31题8分2018年四川成都成都七中嘉祥外国语学校小升初寒假系列训练题C9第17题6分2016年四川成都小升初2018~2019学年浙江杭州西湖区学军小学六年级下学期期末第34题甲容器中有纯酒精11升，乙容器中有水15升，第一次将甲容器中的一部分纯酒精倒入乙容器，使酒精与水混合；第二次将乙容器中的一部分混合液倒入甲容器中，这时甲容器中酒精含量为62.5%，乙容器中酒精含量为25%，那么第二次从乙容器中倒入甲容器的混合液是多少升？7、【来源】2019年浙江杭州西湖区求是教育集团星洲小学六年级上学期单元测试《统计》第11题20克糖完全溶解在80克水中，则该糖水的含糖率为%．8、【来源】2011年四川成都小升初现有浓度为3%的盐水500克，为了制成浓度为4%的盐水，需要蒸发掉克水．9、【来源】2019~2020学年北京朝阳区六年级上学期期中第22题有三杯糖水，甲杯里糖和水的比是1:9；乙杯里用20克糖配成180克糖水；丙杯里先倒入200克水，再加入20克糖；这三杯糖水中，哪杯糖水最甜？写出你的理由．10、【来源】2011~2012学年浙江台州椒江区三甲中心校六年级上学期统测第16题2分现有含盐3%的盐水240克，如果要变成含盐4%的盐水，需加盐克，或蒸发掉水克．1、【答案】甲酒精原有4克，乙酒精原有16克．;【解析】方法一:由“60%和35%的甲和乙两种酒精混合后的纯酒精含量为40%”，可设甲酒精溶液原来有克，乙原来有克，得60%+35%=+×40%；由“如果每种酒精都多取20克，混合后纯酒精的含量变为45%”，得+20×60%++20×35%=++ 40×45%，解方程组即可．设甲酒精溶液原来有克，乙原来有克，得如下两个方程：60%+35%=(+p×40%①(+20)×60%+(+20)×35%=(++40)×45%②，由①得：0.60+0.35=0.4+0.4，即=0.25③，由式②得：0.1−0.15=1式④，把式③代入式④：0.1−0.15×0.25=1，解得：=16，把=16代入③，得：=4．故答案为：甲酒精原有4克，乙酒精原有16克．方法二:2次十字交叉，再利用差不变化连比，也可求．1:1:差:2:2，一份=20÷6−1，1=4（克），1=4×4=16（克），【标注】(浓度十字交叉法)2、【答案】300克．;【解析】500−500×3.2%÷8%=300（克）；答：需要使它蒸发掉300克的水．【标注】(抓不变量)3、【答案】7千克;【解析】除去3千克乙种酒．剩下的11−3=8（千克）中乙、丙两种酒含量相等，这时乙、丙混合酒的含酒精36%+35%÷2=35.5%，剩下的8千克中含酒精38.5%×11−36%×3= 3.155（千克），假设这8千克都是乙、丙混合酒，则含有酒精8×35.5%=2.84（千克），根据“假设法”可求出甲种酒有3.155−2.84÷40%−35.5%=7（千克）．【标注】(浓度十字交叉法)4、【答案】30%．;【解析】方法一:依题意，100克甲瓶盐水与300克乙瓶盐水所含溶质相同，所以，甲瓶盐水的溶质为混合溶液溶质的12，又甲瓶溶液是混合溶液的14，所以甲瓶盐水的浓度为1×15%×12÷14= 30%．答：甲瓶盐水的浓度是30%．方法二:解：设乙瓶盐水的浓度为l，则甲瓶盐水的浓度为3l，根据甲盐+乙盐=总盐列方程：100×3l+300×l=(100+300)×15%，解得=10，则乙瓶盐水的浓度为10%，甲瓶盐水的浓度为30%．【标注】(已知溶质溶液求浓度)(抓不变量)5、【答案】含盐5%的盐水应取200克，含盐8%的盐水取400克来混合;【解析】设取含盐5%的盐水克，则应取含盐8%的盐水600−克．5%+8%600−= 700×6%，5+8600−=700×6，5+4800−8=4200，3=600，=200，600−200=400（克）．所以，含盐5%的盐水应取200克，含盐8%的盐水取400克来混合．【标注】(求用两种浓度配置一种浓度各需要多少)6、【答案】6升．;【解析】第二次乙倒给甲，不改变乙的浓度，所以第一次甲倒给乙后，乙的浓度就已经是25%了；第一次甲倒给乙，100%与15升0%混合成25%，根据十字交叉，5升100%与15升0%混合成20升25%；说明第一次甲倒给乙后，甲乙两容器中的状态为甲：6升100%，乙：20升25%；第二次乙倒给甲，25%与6升100%混合成62.5%，根据十字交叉，6升25%与6升100%混合成12升62.5%；即第二次从乙容器倒出的溶液质量为6升．【标注】(已知溶质浓度求溶液)7、【答案】20;【解析】糖水共有100克，所以含糖率为20÷20+80×100%=20%【标注】(已知溶质溶液求浓度)8、【答案】125;【解析】500×0.03=15，15÷0.04=375，500−375=125克．【标注】(求配置一种浓度需要多少加水的问题)(求配置一种浓度需要多少加水的问题)9、【答案】乙杯最甜．;【解析】甲杯中糖占1份，水占9份，则糖占糖水的110；乙杯中糖占糖水的20÷180=19；丙杯中糖占糖水的20÷(20+200)=111；19>110>111，故乙杯最甜．【标注】(已知溶质溶液求浓度)10、【答案】2.5;60;【解析】240克含盐3%的盐水中，含盐240×3%=7.2克，含水240−7.2=232.8克．要将含盐率变成4%，如果只加盐的话，那么水的质量不变，加盐之后的盐水重量为232.8÷1−4%=242.5克，说明加了242.5−240=2.5克盐．如果只蒸发水的话，那么盐的重量不变，蒸发掉一些水之后，盐水的重量为7.2÷4%=180克，说明蒸发了240−180=60克水．【标注】(百分数浓度问题)(百分数浓度问题)。

以下是一个公考浓度问题示例：
题目描述：实验室有A、B、C三个实验试管，分别装有10克、15克、20克的水，小明把含有一定浓度的10克药水倒进A试管中，混合后取出10克倒入B试管中，再次混合后，从B试管中取出10克倒入C试管中，最后用化学仪器检测出C试管中药水浓度为2%。

问题：小明一开始倒入A试管的药水浓度是多少？
解题思路：
1. 我们可以先计算出A、B、C三个试管中水的总量和药水的总量。

2. 根据C试管中药水浓度为2%，可以计算出C试管中药水质量为2克，水的质量为8克。

3. 根据从B试管中取出10克倒入C试管，我们可以计算出B 试管中药水质量为10×2/8=2.5克，水的质量为7.5克。

4. 根据从A试管中取出10克倒入B试管，我们可以计算出A 试管中药水质量为10×2.5/7.5=3.33克，水的质量为6.67克。

5. 最后，我们可以计算出小明一开始倒入A试管的药水浓度为3.33/10=33.3%。

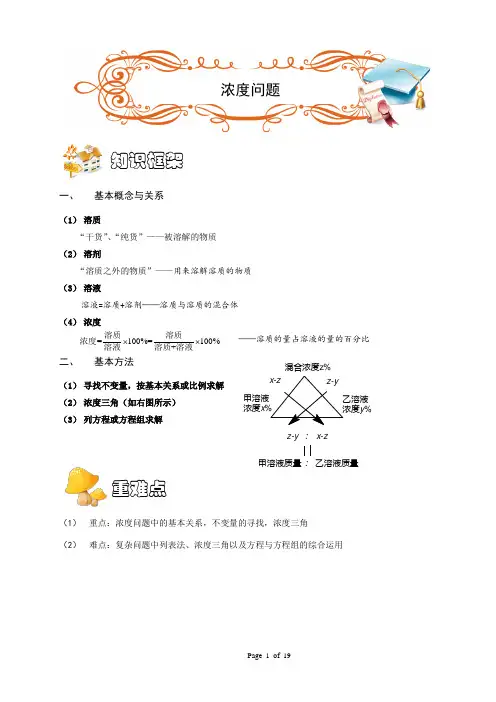
一、 基本概念与关系（1） 溶质“干货”、“纯货”——被溶解的物质 （2） 溶剂“溶质之外的物质”——用来溶解溶质的物质 （3） 溶液溶液=溶质+溶剂——溶质与溶质的混合体 （4） 浓度——溶质的量占溶液的量的百分比 二、 基本方法（1） 寻找不变量，按基本关系或比例求解 （2） 浓度三角（如右图所示） （3） 列方程或方程组求解（1） 重点：浓度问题中的基本关系，不变量的寻找，浓度三角 （2） 难点：复杂问题中列表法、浓度三角以及方程与方程组的综合运用重难点知识框架浓度问题=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-zz-yx-z乙溶液浓度y %浓度x %混合浓度z%一、抓住不变量和浓度基本关系解决问题【例 1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到，那么这种溶液的食盐浓度为多少？【考点】浓度问题【难度】2星【题型】解答【解析】两种配置溶液共含食盐40×15%+60×10%=12克，而溶液质量为40+60-50=50克，所以这种溶液的浓度为12÷50=24%.【答案】24%【巩固】一容器内有浓度为25％的糖水，若再加入20千克水，则糖水的浓度变为15％，问这个容器内原来含有糖多少千克？【考点】浓度问题【难度】2星【题型】解答【解析】100100207.51525⎛⎫÷-=⎪⎝⎭. 所以原来含有糖7.5千克.【答案】7.5【例 2】浓度为20％的糖水40克，要把它变成浓度为40％的糖水，需加多少克糖？【考点】浓度问题【难度】2星【题型】解答【解析】浓度为20％，含糖40×20％＝8（克），有水40- 8＝32（克）.如果要变成浓度为40％，32克水中，应该含有的糖为：32÷（1－40%）－32＝1213（克），需加糖112181333-=（克）.【答案】1 133【巩固】浓度为10％，重量为80克的糖水中，加入多少克水就能得到浓度为8％的糖水？【考点】浓度问题【难度】2星【题型】解答【解析】浓度10％，含糖80×10％＝8（克），有水80-8＝72（克）.如果要变成浓度为8％，含糖8克，例题精讲糖和水的总重量是8÷8％＝100（克），其中有水100-8＝92（克）.还要加入水 92- 72＝ 20（克）.【答案】20【例 3】 买来蘑菇10千克，含水量为99％，晾晒一会儿后，含水量为98％，问蒸发掉多少水份？【考点】浓度问题【难度】2星 【题型】解答【解析】 晾晒只是使蘑菇里面的水量减少了，蘑菇里其它物质的量还是不变的，所以本题可以抓住这个不变量来解．原来鲜蘑菇里面其它物质的含量为()10199%0.1⨯-=千克，晾晒后蘑菇里面其它物质的含量还是0.1千克，所以晾晒后的蘑菇有()0.1198%5÷-=千克．【答案】5【巩固】 1000千克葡萄含水率为96.5%，一周后含水率降为96%，这些葡萄的质量减少了 千克.【考点】浓度问题 【难度】2星 【题型】填空【解析】 因为减少的是水的质量，其它物质的质量没有变化，设葡萄糖质量减少了x ，则有1000(196.5%)(1000)(196%)x ⨯-=-⨯-，解得125x =.【答案】125【例 4】 将含农药30%的药液，加入一定量的水以后，药液含药24%，如果再加入同样多的水，药液含药的百分比是________．【考点】浓度问题 【难度】3星 【题型】填空【解析】 开始时药与水的比为3:7，加入一定量的水后，药与水的比为24:766:19=，由于在操作开始前后药的重量不变，所以我们把开始时药与水的比化为6:14，即，原来药占6份，水占14份；加入一定量的水后，药还是6份，水变为19份，所以加入了5份的水，若再加入5份的水，则水变为24份，药仍然为6份，所以最后得到的药水中药的百分比为：6(624)100%20%÷+⨯=．【答案】20%【巩固】 一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，盐水的含盐百分比变为12%，第三次再加入同样多的水，盐水的含盐百分比将变为_______%.【考点】浓度问题 【难度】3星 【题型】填空【解析】第一次加水后盐水和盐的比为20：3，第二次加水后变为25：3，所以第三次加水后变为30：3，所以盐水的含盐百分比为3÷30×100%=10% .【答案】10%二、通过浓度三角解决浓度和实际生活中的配比问题【例 5】有浓度为20％的盐水300克，要配制成40％的盐水，需加入浓度为70％的盐水多少克？【考点】浓度问题【难度】2星【题型】解答【解析】将两种溶液的浓度分别放在左右两侧，重量放在旁边，配制后溶液的浓度放在正下方，用直线相连；（见图1）直线两侧标着两个浓度的差，并化成简单的整数比。

知识要点 浓度问题的内容与我们实际的生活联系很紧密，就知识点而言它包括小学所学2个重点知识：百分数，比例。

1、 浓度问题中的基本量：1）溶质：通常为盐水中的“盐”，糖水中的“糖”，酒精溶液中的“酒精”等2）溶剂：一般为水，部分题目中也会出现煤油等3）溶液：溶质和溶液的混合液体。

4）浓度：溶质质量与溶液质量的比值。

2、 在同一种重量单位里，溶质、溶剂、溶液以及浓度之间有以下关系：浓度=100%100%⨯=⨯溶质重量溶质重量溶质重量+溶剂质量溶液重量3、 有关浓度配比问题还经常用到下面的关系式：=+溶液重量溶质重量溶剂重量=÷溶液重量溶质重量浓度1=⨯-溶剂重量溶液重量（浓度）4、 浓度问题主要分为下列四种，应用相应技巧处理往往事半功倍：①稀释问题：由浓度高的溶液经过添加溶剂变成浓度低的溶液的过程成为稀释。

在这种稀释的过程中，只是溶剂增加了，溶质的重量是不变的，这是解这类问题的关键。

②加浓问题：由浓度低的溶液经过添加溶质或蒸发掉溶剂的方式转化为浓度高的溶液的过程成为加浓。

在这个加浓的过程中，既可添加溶质又可蒸发掉溶剂，要根据题目的条件，选择恰当的方式，正确解答。

③两种溶液的配制问题：在浓度问题中有这样一类题，是把原有的两种或两种以上不同重量、不同浓度的溶液，混合在一起配成某种新浓度的溶液。

这是浓度的配制问题，解这类问题较多的是利用列方程的方法解答，因为混合前后的溶质是不变的。

④溶液互换问题：浓度中溶液互换问题，就是先后把一个容器的溶液倒入对方容器中，再求混合后各自的浓度等问题。

解答这类问题，要认真审题，分步解答，必要时可采取列表法分析解答。

浓度问题基本浓度问题1.（1）将10克糖溶入100克水中，该糖水的浓度是多少？（精确到0.1%）（2）一个容器中装有20%的酒精溶液1000克，那么该容器的酒精是多少克？【解析】 （1）因为浓度=100%⨯溶质质量溶液质量，所以该糖水浓度为10100%9.1%10+100⨯≈ （2）因为溶质重量=溶液重量⨯浓度，所以该容器中的纯酒精为100020%=200⨯（克）2.将75％的酒精溶液32克稀释成浓度为40％的稀酒精，需加入水多少克？【解析】 稀释时加入的水溶液浓度为0％（如果需要加入干物质，浓度为100％），标注数值的方法与例1相同。

六年级数学上册《浓度问题》应用题，考试必考溶液的重量=溶质的重量+溶剂的重量浓度=溶质质量÷溶液重量x 100%1.浓度为10%的盐水60克，加入多少克盐，可以使其浓度为20%？提示：加盐，则盐水中水不变，现在的盐水比原盐水多的量即增加的盐。

解：加盐前水的量：60 x（1-10%）= 54 （克）加盐后盐水的总量：54 +（1- 20%）= 67.5 （克）67.5 - 60 = 7.5 （克）答：加7.5克盐，可以使浓度变为20%。

2.浓度为20%的盐水60克，蒸发多少克水使其浓度为25%？提示：水蒸发后盐不变,根据现在的浓度，你知道现在的盐水是多少吗？解：蒸发前后盐的重量：60 x 20% = 12（克）蒸发后盐水的总重量：12 + 25% = 48（克）60 - 48 = 12（克）答：蒸发12克水后可以使其浓度变为25%。

3.100克浓度为15%的盐水和25克浓度为20%的盐水混合。

混合后浓度是多少？提示：混合后，两种浓度的盐共有多少克？盐水共有多少克？解：盐的总重量：100 x 15% + 25 x 20% = 20（克）盐水的总重量：100 + 25 = 125（克）混合后的浓度：20 + 125 x 100% = 16% 答：混合后浓度是16%。

4.要想得到浓度为20%的盐水360克，需15%的盐水和25%的盐水各多少克？提示：设需15%的盐水χ克后，则需25%的盐水多少克？解：设需要15%的盐水χ克，则需要25%的盐水（360-χ）克。

15%+25%（360- χ）=360x 20%χ=180360 - 180=180（克）答：需要15%的盐水180克，25%的盐水180克。

小升初数学运用题真题汇编典型运用题—浓度问题班级姓名得分知识梳理基础题1. （新疆巴音郭楞六年级期末）浓度为70%的酒精溶液500克，其中的纯酒精是多少克？2.（河北保定六年级期末）李老师每天对教室地面和桌子表面进行消毒。

桶里有6.4升水，根据说明，需要加入多少消毒液？某种消毒液配比浓度说明一般污染物体表面消毒：按消毒液与水1:10的比例稀释，喷洒物体30分钟。

餐饮器具消毒：按消毒液与水1:80的比例稀释，浸泡20分钟。

3.（山东潍坊六年级期末）有大、小两盒橙汁，如图。

哪盒橙汁的浓度高一些？4.（福建三明六年级期末）这是某种清洁剂浓缩液的稀释瓶，瓶上标明的比表示浓缩液和水的体积之比，按照这些比可以配出不同浓度的稀释液。

妈妈用50毫升的浓缩液，按1:5的比配出了一瓶稀释液，这瓶稀释液的体积是多少毫升？5.（广东揭阳小升初考试）某种消毒液是一种高效消毒剂，需要通过稀释才能使用，学校总务处准备配制消毒液进行消毒。

现在有20毫升消毒原液，要兑成浓度为1%的消毒液需要加入多少升水？6.（重庆南开中学小升初招生）把100克含盐30%的盐水稀释成含盐24%的盐水，还需要加水多少克？提高题7.（重庆一外小升初招生）现有350克浓度为20%的糖水，要变成浓度为30%的糖水，需要加糖多少克？8.（广东揭阳小升初考试）笑笑按照说明书上1:4的比例调制了一杯100毫升的蜂蜜水给妈妈喝，妈妈尝了一口，说：“笑笑，你把这杯水的甜味调得再淡些吧，浓度是10%就可以了。

”你能帮笑笑想想办法吗？请通过列式计算说明你的方法。

9.（湖南中雅培粹中学小升初招生）浓度为70%的酒精溶液500克与浓度为50%的酒精溶液300克，混合后所得到的酒精溶液的浓度是多少？培优题10.（河南浚县科达小学六年级期末）有含盐5%的盐水80千克，要配制含盐9%的盐水280千克，需加入的盐水的浓度为百分之几？11.（河北石家庄小升初考试）有浓度为30%的糖水若干，加了一定量的水后稀释成24%的糖水，如果再加入同样多的水后，浓度将变为多少？12.（江西崇仁六年级期末）杯子里有浓度为80%的酒精100克，第一次从中倒出10克这种酒精。

浓度问题专题
※溶液的质量=溶液的质量+溶剂的质量
※浓度=溶质的质量+溶液的质量
1.有含糖量为7%的糖水600克，要使其含糖量加大到10%，需要再加入多少克糖？
2.现有浓度为20%的糖水300克，要把它变成浓度为40%的糖水，需要加糖多少克？
3.有含有盐15%的盐水20克，要使盐水的浓度为20%，需要加盐多少千克？
4.一种35%的农药，如稀释到1.75%时，治虫最有效，用多少千克浓度为35%的农药加多少千克水，才能配成1.75%的农药800千克？
5.用含氨0.15%的氨水进行油菜追肥，现有含氨16%的氨水30千克，配制时需要加水多少千克？
6.仓库运来含水量为90%的一种水果100千克，一星期后再测，发现含水量降低到80%现在这批水果的质量是多少千克？
7.一容器内装有10升纯酒精，倒出2.5升后，用水加满，再倒出5升，再用水加满，这时容器内溶液的溶度是多少？
8.现在有浓度为10%的盐水20千克，再加上多少千克浓度为30%的盐水，可以得到浓度22%的盐水？
9.在100千克浓度为50%的硫酸溶液中，再加多少千克浓度为5%硫酸溶液就可以配成25%的硫酸溶液？
10.在20%的盐水中加入10千克水，浓度为15%，再加入多少千克盐，浓度为25%？
11.将20%的盐水与5%的盐水混合，配成15%的盐水600克，需要20%的盐水和5%的盐水各多少克？
12.甲桶有糖水60千克，含糖率为40%乙桶有糖水40%千克，含糖率为20%要使得两桶糖水的含糖率相等，需要把两桶的糖水互相交换多少千克？
13.两种钢分别含镍5%和40%，要得到140%含镍30%的钢，需要含镍5%的钢和含镍40%的钢各多少吨？。

小学六年级奥数题及答案解析：浓度问题1.浓度问题2.浓度应用题乙两只装满硫酸溶液的容器，甲容器中装有浓度为8％的硫酸溶液600千克，乙容器中装有浓度为40％的硫酸溶液400千克.各取多少千克分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样？由题意知，从甲、乙两容器中各取出一定量的溶液放入对方容器中，最终要达到两容器中溶液的浓度相等，在这个变化过程中，两容器中溶液的重量并没有改变。

不妨设从甲、乙两容器中各取出硫酸溶液x千克放入对方容器中，可使甲、乙两容器中硫酸溶液的浓度相等.这时甲容器中硫酸的重量可表示为（600-x）8％＋x 40％=48＋32％x.甲容器中溶液的浓答：应从两容器中各取出240千克溶液放入对方容器中，才能使两容器中硫酸溶液的浓度相同。

上述问题还可以这样考虑：由于交换前后两容器中溶液的重量均没有改变，而交换一定量的硫酸溶液其目的是将原来两容器中溶液的浓度由不同变为相同，而且交换前后两容器内溶液的重量之和也没有改变，根据这个条件我们可以先计算出两容器中的溶液浓度达到相等时的数值，从而再计算出应交换的溶液的量：甲容器中纯硫酸的重量为600 8％=48（千克）；乙容器中纯硫酸的重量为400 40％=160（千克）；两容器中纯硫酸的重量和为48＋160=208千克，硫酸溶液的重量和为600＋400=1000千克。

两容器中溶液混合后浓度为208 1000=20.8％。

所以应交换的硫酸溶液的量为：（600 20.8％-600 8％）（40％-8％）=240（千克）答：应从两容器中各取出240千克放入对方容器中，才能使两容器中硫酸溶液的浓度一样。

3.应用题育红小学四年级学生比三年级学生多25％，五年级学生比四年级学生少10％，六年级学生比五年级学生多10％。

如果六年级学生比三年级学生多38人，那么三至六年级共有多少名学生？分析：以三年级学生人数为标准量，则四年级是三年级的125％，五年级是三年级的125％（1-10％），六年级是三年级的125％（1-10％）（1+10％）。

华杯赛应用题专题：11浓度问题问题：将糖溶于水中就得到了糖水，那么糖水甜的程度由什么决定呢？糖水甜的程度是由糖与糖水重量的比值决定的，这个比值称为糖水的浓度，一般用百分数表示。

其中糖叫做溶质，水叫做溶剂，整杯糖水叫做溶液。

你还能举出一些生活中见过的溶液吗？基本关系：溶液的重量＝溶质的重量＋溶剂的重量浓度＝溶质的重量÷溶液的重量（请你由此分析一下浓度的取值范围）例1.一容器内有浓度为25%的糖水，若再加入20千克水，则糖水的浓度变为15%，问这个容器内原来含有糖多少千克？【答案】7.5千克【解答】解法一：原糖水浓度为25%，说明原溶液重量是糖的4倍，设糖的重量为单位1，则糖水的总重量为4。

加入20千克水以后，浓度变为15%，这时溶液重量是1÷15%＝。

多出的部分就是加入的水，因此20千克水所占的份数是。

那么原有糖的重量（单位1）为千克。

解法二：设原有糖水x千克，则可列方程：x×25%＝（x＋20）×15%解得x＝30，那么原有糖30×25%＝7.5千克。

例2.现有浓度为10%的盐水20千克，再加入多少千克浓度为30%的盐水，可以得到浓度为22%的盐水？【答案】30千克【解答】解法一：设需要加入x千克盐水，可列方程：20×10%＋x×30%＝（x＋20）×22%解得x＝30解法二：原有溶质20×10%＝2千克，混合后20千克溶液中含有溶质20×22%＝4.4千克，多出的部分是新加入的溶液中比22%多的盐补充进来的，因此需要加入的溶液重量为：（4.4－2）÷（30%－22%）＝30千克请你观察题目中出现的数据：例3.有A、B两瓶不同浓度的盐水，小明从两瓶中各取1千克混合在一起，得到一份浓度为27%的盐水.他又将这份盐水与1千克A瓶盐水混合在一起，最终浓度为29%.那么B 瓶盐水的浓度是多少？【答案】21%【解答】浓度问题问题：将糖溶于水中就得到了糖水，那么糖水甜的程度由什么决定呢？糖水甜的程度是由糖与糖水重量的比值决定的，这个比值称为糖水的浓度，一般用百分数表示。

百分数应用题•浓度问题1．有含盐15%的盐水20千克，要使盐水的浓度为20%，需加盐多少千克？20×15%＝3（千克）（20－3）÷（1－20%）＝17÷0.8＝21.25（千克）21.25－20＝1.25（千克）答：需加盐1.25千克。

2．一种35%的新农药，如稀释到1.75%时，治虫最有效，用多少千克浓度为35%的农药加多少千克水，才能配成1.75%的农药800千克？纯农药：800×1.75%＝14（千克）新农药：14÷35%＝40（千克）800－40＝760（千克）答：用40千克浓度为35%的农药加760千克水。

3．100克浓度为55%的酒精溶液中，需加入多少克的水，才能成为浓度是40%的酒精的溶液？100×55%＝55（克）55÷40%＝137.5（克）137.5－100＝37.5（克）答：需加入37.5克的水。

百分数应用题•浓度问题4．甲容器中有8%的盐水300克，乙容器中有12.5%的盐水120克，往甲、乙两个容器分别倒入等量的水，使两个容器中盐水的浓度一样。

每个容器应倒入多少克水？180克300×8%＝24（克）120×12.5%＝15（克）解：设每个容器应倒入x克水。

24÷（300＋x）＝15÷（120＋x）24×（120＋x）＝15×（300＋x）2880＋24x＝4500＋15x9x＝1620x＝180答：每个容器应倒入180克水。

5．有两种酒精，一种含水15%，另一种含水5%，配制浓度为88%的酒精500克，每种酒精各取多少克？解：设含水15%的取x克，则含水5%的取500－x克。

（1－15%）x＋（1－5%）×（500－x）＝88%×5000.85x＋0.95×（500－x）＝0.88×5000.85x＋475－0.95x＝4400.1x＝35x＝350500－350＝150（克）答：含水15%的取350克，则含水5%的取150克。

浓度问题综合（二）知识框架一、浓度问题定义：有关浓度的问题，在我们的日常生活和生产实际中经常会遇到.在这部分内容里我们对有关浓度的问题做一些初步的探讨。

例如将糖溶于水就得到了糖水，而糖水甜的程度是由什么决定的呢？我们不妨来做一个小实验：在两只同样大小的杯子中放入相同量的水，再往两只杯子中分别放入白糖，使其中一只杯子中的糖是另一只杯子中的糖的2倍，品尝一下，有什么感觉.我们很容易发现，放糖多的杯子中的水甜.若将等量的糖放入两只杯子中，在两只杯子中放入不等量的水，比如一只杯子中放入的水的量是另一只杯子中放入水的量的2倍，这时结果会怎样呢？不难想象到放水少的杯子中的糖水甜.通过上面的小实验我们可以知道，糖水甜的程度是由糖与糖水二者重量的比值决定的.糖与糖水重量的比值叫糖水的浓度（也叫含糖率）.这个比值一般我们将它写成百分数，所以称为百分比浓度.其中糖叫溶质，水叫做溶剂，糖水叫溶液，解答这类浓度问题的主要依据有：浓度＝溶液重量溶质重量×100% 这个式子还可以转化为：溶质质量溶质质量+溶剂质量×100％ 溶液的重量=溶质的重量+溶剂的重量浓度=溶质重量÷溶液重量溶液重量=溶质重量÷浓度溶质重量=溶液重量×浓度二、解浓度问题的重要方法：1、利用浓度的基本定义以及三个量之间的关系：2、列方程解应用题也是解决浓度问题的重要方法。

解答浓度问题，首先要弄清什么是浓度。

有些问题根据题意列方程解答比较容易，在列方程时，要注意寻找题目中数量问题的相等关系。

溶度问题包括以下几种基本题型︰（1） 溶剂的增加或减少引起浓度变化。

面对这种问题，不论溶剂增加或减少，溶质是始终不变的，据此便可解题。

（2） 溶质的增加引起浓度变化。

面对这种问题，溶质和浓度都增大了，但溶剂是不变的，据此便可解题。

（3） 两种或几种不同溶度的溶液配比问题。

面对这种问题，要抓住混合前各溶液的溶质和与混合后溶液的溶质质量相等，据此便可解题。

分数、百分数应用题（二）（浓度问题）例1：在浓度为10%、重量为80克的盐水中，加入多少克水就能得到浓度是8%的盐水？解：设加入x 克水能得到浓度为8%的盐水。

80×10%=[x ＋80×（1－10%）]×8% 解之得：x=24例 2：现有浓度为20%的糖水300克，要把它变成浓度是40%的糖水，需加糖多少克？解：设需加糖x 克能得到浓度为40%的糖水。

300%40%20300+=++x x 解之得：x=100 例3：将20%的盐水与5%的盐水混合，配制成15%的盐水600克。

需要20%的盐水和5%的盐水各多少克？解：设20%的盐水为x 克，5%的盐水为（600－x ）克。

20%x ＋（600－x ）×5%=600×15% 解之得：x=400 5%的盐水：（600－x ）=200克。

例4：甲容器中有8%的盐水300克，乙容器中有12.5%盐水120克往甲、乙两个容器中分别倒入等量的水，使两个容器中盐水的浓度一样。

每个容器应倒入水多少克？解：设需加水x 克，300×8%:（300＋x ）=120×12.5%:（120＋x ） 解之得：x=180。

例5：A 、B 、C 三个试管中各盛有10克、20克、30克水。

把某种浓度的盐水10克倒入A 中，混合后取出10克倒入B 中，再混合后又从B 中取出10克倒入C 中，现在C 中的盐水浓度是0.5%。

最早倒入A 中的盐水浓度是百分之几？ 解：102010301040%50⨯⨯⨯.=20% 练习：1、一瓶盐水共重200克，其中盐有10克，这瓶盐水的浓度是 （ ）。

2、配制一种盐水，在480克水中加20克盐，这种盐水的浓度是 （ ）。

3、一种糖水的浓度是15%，300克糖水中含糖（ ）克。

4、一种糖水的浓度是10%，12克糖需加水（ ）克。

5、在浓度为15%，重量为200克的糖水中，加入多少克水就能得到浓度是10%的糖水？6、浓度为10%的糖水300克，要把它变成浓度为25%，需要加糖多少克？7、有浓度为2.5%的盐水200克，为了制成浓度3.5%的盐水，从中要蒸发掉多少克水？8、两种钢分别含镍5%和40%，要得到140吨含镍30%的钢。

浓度问题答案典题探究例1．现有浓度为20%的盐水400g，要把它变成浓度为40%的盐水，需要加入多少盐？或水减少多少克？考点：浓度问题．专题：浓度与配比问题．分析：（1）浓度为20%的盐水400克，含水的质量为400×（1﹣20%）=320（克），浓度为40%的盐水重量是320÷（1﹣40%），计算出结果，再减去400克即可．（2）根据题意，水的重量变了，但盐的重量始终未变，于是可先求出盐的重量：400×20%=80（克），后来的盐还是80克，占盐水的40%，所以后来盐水重量为80÷40%=200（克），水减少了400﹣200=200（克）．解答：解：（1）400×（1﹣20%）÷（1﹣40%）﹣400=400×0.8÷0.6﹣400≈533﹣400=133（克）答：需要加入133克盐．（2）400﹣400×20%÷40%=400﹣200=200（克）答：水减少200克．点评：此题解答的关键在于抓住不变量这一重要条件，逐步求解．例2．现在有溶液两种，甲为50%的溶液，乙为30%的溶液，各900克，现在从甲、乙两溶液中各取300克，分别放到乙、甲溶液中，混合后，再从甲、乙两溶液中各取300克，分别放到乙、甲溶液中，…，问（1）第一次混合后，甲、乙溶液的浓度各是多少？（2）第四次混合后，甲、乙溶液的浓度各是多少？（3）猜想，如果这样无穷反复下去，甲、乙溶液的浓度将是多少？考点：浓度问题．专题：浓度与配比问题．分析：（1）要求混合后所得到的溶液的浓度是多少，根据一个数乘分数的意义先分别求出两种溶液中的纯酒精重量，然后根据“×100%=百分比浓度”，代入数值进行解答即可．（2）根据上题的计算经过和计算的结果，找出两种溶液中溶质变化的规律，从而找出计算每次溶液混合后浓度的方法，进而求出第四次混合后的浓度．（3）根据上题计算出浓度的结果进行猜想，求解即可．解答：解：（1）从甲中取出的300克，含有溶质：300×50%=150（克），甲剩余溶质（900﹣300）×50%=300（克）从乙中取出的300克，含有溶质300×30%=90（克），乙剩余溶质（900﹣300）×30%=180（克）；混合后，甲含溶质300+90=390（克），浓度为：390÷900×100%≈43.33%；乙含溶质：180+150=330（克），浓度为330÷900×100%≈36.67%；答：第一次混合后的甲的浓度是43.33%，乙的浓度是36.67%．（2）观察一下这个结果，发现在混合之前，甲总共含有溶质900×50%=450（克），混合后为390克，少了60克；在混合之前，乙总共含有溶质900×30%=270（克），混合后为330克，多了60克；得出结论：60克溶质发生了转移，而且60=300×（50%﹣30%），也就是说，转移的溶质=初始浓度差×300；第二次浓度差：43.33%﹣36.67%=6.66%．转移溶质300×6.66%=19.98（克），甲浓度（900×43.33%﹣19.98）÷900×100%≈41.11%，乙浓度（900×36.67%+19.98）÷900×100%≈38.89%；第三次浓度差：41.11%﹣38.89%=2.22%；甲浓度（900×41.11%﹣300×2.22%）÷900×100%=40.37%，乙浓度（900×38.89%+300×2.22%）÷900×100%=39.63%；第四次浓度差：40.37%﹣39.63%=0.74%；300×0.74%=2.22（克）；甲的浓度是：（900×40.37%﹣2.22）÷900×100%≈40.12%；乙的浓度是：（900×39.63%+2.22）÷900×100%≈39.88%；答：第四次混合后，甲溶液的浓度是40.12%，乙的浓度是39.88%．（3）从上面的推理可以看出，两者的浓度是越来越接近的，所以说无限次混合，必然是甲乙浓度相等，均为：（900×50%+900×30%）÷（900×2）×100%=40%．答：如果这样无穷反复下去，甲、乙溶液的浓度将是40%．点评：解决本题关键是把握住甲、乙的质量始终是900克这一点，多次计算后即可以发现规律．例3．甲种酒精的纯酒精含量为72%，乙种酒精的纯酒精含量为58%，两种酒精各取出一些混合后纯酒精的含量为62%．如果两种酒精所取的数量都比原来多15升，混合后纯酒精的含量就为63.25%．求第一次混合时，甲、乙两种酒精各取了多少升？考点：浓度问题．专题：浓度与配比问题．分析：混合后纯酒精含量为62%，则甲乙种酒精体积比（62﹣58）：（72﹣62）=2：5，混合后纯酒精含量为63.25%，则甲乙种酒精体积比（63.25﹣58）：（72﹣63.25）=3：5，原因是每种酒精取的数量比原来都多取15升，设第一次混合时，甲、乙两种酒精应各取2x升、5x升，则（2x+15）：（5x+15）=3：5，解比例求出x的值，进一步得出2x、5x的值．解答：解：混合后纯酒精含量为62%，则甲乙种酒精体积比（62﹣58）：（72﹣62）=2：5，设第一次混合时，甲、乙两种酒精应各取2x升、5x升，（2x+15）：（5x+15）=3：5，5（2x+15）=3（5x+15），10x+75=15x+45，10x+75﹣10x=15x+45﹣10x，5x+45=75，5x+45﹣45=75﹣45，5x=30，5x÷5=30÷5，x=6，2×6=12，5×6=30答：甲种酒精应取12升、乙种酒精取30升．点评：解决此题的关键是根据甲乙种酒精体积比（62﹣58）：（72﹣62）=2：5，混合后纯酒精含量为63.25%，则甲乙种酒精体积比（63.25﹣58）：（72﹣63.25）=3：5，取的数量比原来都多取15升，得出（2x+15）：（5x+15）=3：5．例4．在浓度为40%的酒精溶液中加入5千克水，浓度变为30%．再加入多少千克纯酒精，浓度才能变为50%？考点：浓度问题．分析：设原来酒精溶液为x千克，则原溶液中酒精的质量x×40%，加入水后酒精的质量不变但溶液质量增加，所以可求出原来盐酒精的质量；同样加入酒精后酒精溶液的质量=x×40%+y，溶液质量=x+5+Y，从而依据浓度公式列式求解．解答：解：设原来有酒精溶液x千克，40%x÷（x+5）=30%，0.4x=0.3×（x+5），0.4x=0.3x+1.5，0.1x=1.5，x=15；设再加入y克酒精，（15×40%+y）÷（15+5+y）=50%，6+y=0.5×（20+y），6+y﹣0.5y=10+0.5y﹣0.5y，6+0.5y﹣6=10﹣6，0.5y÷0.5=4÷0.5，y=8，答：再加入8千克酒精，可使酒精溶液的浓度提高到50%．点评：此题主要考查百分数的实际应用，关键先求原来酒精溶液的重量．例5．小明到商店买红、黑两种笔共66支．红笔每支定价5元，黑笔每支定价9元．由于买的数量较多，商店就给予优惠，红笔按定价85%付钱，黑笔按定价80%付钱，如果他付的钱比按定价少付了18%，那么他买了红笔多少支？考点：浓度问题．分析：浓度倒三角的妙用：红笔按85%优惠，黑笔按80%优惠，结果少付18%，相当于按82%优惠，可按浓度问题进行配比．与其他题不同的地方在于红、黑两种笔的单价不同，要把这个因素考虑进去．然后就可以按比例分配这66支笔了．解答：解：1﹣18%=82%；红笔每支多付：5×（85%﹣82%），=5×3%，=0.15（元）；黑笔每支少付：9×（82%﹣80%），=9×2%，=0.18（元）；红笔总共多付的钱等于黑笔总共少付的钱，红笔与黑笔数量之比是0.15与0.18的反比，即：0.18：0.15=6：5，红笔是：66×=36（支），答：他买了红笔36支．点评：解答此题的关键是求出红笔与黑笔数量之比，然后根据按比例分配的方法解答即可．演练方阵A档（巩固专练）一．选择题（共2小题）1．在12千克含盐15%的盐水中加水，使盐水中含盐9%，需要加水（）千克．A．6B．8C．12D．20考点：浓度问题．分析：根据一个数乘分数的意义，先用“12×15%”计算出12千克盐水中含盐的重量，即1.8千克；进而根据“盐的重量不变”，得出后来盐水的9%是1.8千克；根据已知一个数的几分之几是多少，求这个数，用除法计算出后来盐水的重量，继而用“后来盐水的重量﹣原来盐水的重量”解答即可．解答：解：原来含盐：12×15%=1.8（千克），1.8÷9%﹣12，=20﹣12，=8（千克）；故答案为：B．点评：解答此题的关键：抓住不变量，即盐的重量不变，进行分析，解答，得出结论．2．有两种酒精溶液，甲溶液的浓度是75%，乙溶液的浓度是15%，现在要将这两种溶液混合成浓度是50%的酒精溶液18升，应取甲溶液（）升．A．7.5B．10.5C．6.5D．11.5考点：浓度问题．专题：浓度与配比问题．分析：此题可用方程解答，设需要甲溶液x升，则需要乙溶液（18﹣x）升，根据溶质质量相等，可列方程75%x+15%×（18﹣x）=50%×18，解方程即可．解答：解：设需要甲溶液x升，则需要乙溶液（18﹣x）升，由题意得75%x+15%×（18﹣x）=50%×180.75x﹣0.15x=6.30.6x=6.3x=10.5答：需要甲溶液10.5升．故选：B．点评：此题考查学生有关浓度的问题，解题的关键是根据溶质相等列出方程．二．填空题（共4小题）3．有浓度为10%的盐水170克，加入10克盐后，盐水的浓度为15%．考点：浓度问题．专题：浓度与配比问题．分析：由“浓度为10%的盐水170克”可求出含水量，即170×（1﹣10%）克，因为前后含水量不变，因此后来的盐水质量为170×（1﹣10%）÷（1﹣15%）克，然后减去原来的盐水质量，即为所求．解答：解：170×（1﹣10%）÷（1﹣15%）﹣170，=170×0.9÷0.85﹣170，=180﹣170，=10（克）；答：加入10克盐后，盐水的浓度为15%．故答案为：10点评：抓住含水量不变这一关键条件，求出后来的盐水质量，进而解决问题．4．现有甲、乙、丙三个桶，甲中装有500克水，乙中装有浓度为40%的盐水800克，首先将甲中水的一半倒入乙，然后将乙中盐水的一半倒入丙，再将丙中盐水的一半倒入甲，这算进行一轮操作，那么进行了两轮操作后甲桶中纯盐有130克，盐水的浓度是22.1%（精确到小数点后一位）考点：浓度问题．专题：浓度与配比问题．分析：由乙中装有浓度为40%的盐水800克，可求出乙中盐的含量：800×40%=320克，甲中水的一半倒入乙，这时乙中盐没变是320克，盐水重量变了是800+500÷2=1050；然后将乙中盐水的一半倒入丙这时盐的重量是320÷2=160克，盐水变成1050÷2=525克；再将丙中盐水的一半倒入甲，这时甲中盐160÷2=80，盐水重量250+525÷2=512.5克；第二轮甲中盐水的一半倒入乙这时乙中盐是80÷2+320÷2=200克，盐水重量变了是512.5÷2+1050÷2=781.25克，再将乙中盐水的一半倒入丙，这时盐变成200÷2+160=260克，盐水重量525+781.25÷2=915.625克，再将丙中盐水的一半倒入甲，这时甲中盐的含量：260÷2+40=170克，盐水重量变了512.5÷2+915.625÷2=714.063克，再根据求浓度的方法计算即可．解答：解：由乙中装有浓度为40%的盐水800克，可求出乙中盐的含量：800×40%=320克；甲中水的一半倒入乙，这时乙中盐没变是320克，盐水重量变了是800+500÷2=1050；然后将乙中盐水的一半倒入丙这时盐的重量是320÷2=160克，盐水变成1050÷2=525克；再将丙中盐水的一半倒入甲，这时甲中盐160÷2=80克，盐水重量250+525÷2=512.5克；第二轮甲中盐水的一半倒入乙这时乙中盐是80÷2+320÷2=200克，盐水重量变了是512.5÷2+1050÷2=781.25克；再将乙中盐水的一半倒入丙，这时盐变成200÷2+160÷2=180克，盐水重量525÷2+781.25÷2=653.125克；再将丙中盐水的一半倒入甲，这时甲中盐的含量：180÷2+40=130克，盐水重量变了512.5÷2+653.125÷2=589.063克；盐水的浓度是：130÷589.063×100%≈22.1%，答：甲桶中纯盐有130克，盐水的浓度是22.1%．点评：最关键的思维是要抓住题中每次都到出一半，就求出盐的一半，盐水的一半，以此类推，最后根据求浓度的公式求出即可．5．地震灾区为了进行卫生防疫，用一种浓度为35%的消毒药水，稀释到1.75%时效果最好．现需要配制浓度为1.75%的消毒液800千克，则需要浓度为35%的消毒药水40千克，加水760千克．考点：浓度问题．分析：首先要明白：药+水=药水，药水的浓度是：药占药水的百分之几．要配制浓度为1.75%的消毒液800千克，则800千克药水中所含的药即可求出（800×1.75%），即14千克．因为是用35%的药水配制而成，因此，所需要浓度为35%的药水数就可求出，即：14÷35%．最后用800千克减去40千克即为所加水的重量，分步列式解答即可．解答：解：（800×1.75%）÷35%，=14÷35%，=40；800﹣40，=760（千克）．答：需要浓度为35%的消毒液水40千克，需加水760千克．故答案为：40，760．点评：解答此题的关键是：求800千克浓度为1.75%的药水中所含的药是多少千克．6．A，B，C三个瓶子分别盛有100，200，300克水，把1OO克酒精溶液倒入A瓶中混合后取出1O0克倒入B瓶，再混合100克倒入c瓶，最后C瓶酒精含量为2，5%则最初倒入A瓶的酒精溶液的酒精含量是60%考点：浓度问题．专题：传统应用题专题．分析：混合后，三个试管中的酒精溶液分别是200克、300克、400克，又知C管中的浓度为2.5%，可算出C管中的酒精是：400×2.5%=10（克）．由于原来C管中只有水，说明这10克的酒精溶液来自从B管中倒入的100克酒精溶液里．B管倒入C管的酒精溶液和留下的酒精溶液浓度是一样的，100克酒精溶液中有10克酒精，那么原来B管300克酒精溶液就应该含酒精：10×3=30（克）．而且这30克酒精来自从A管倒入的100克酒精溶液中．A管倒入B管的酒精溶液和留下的酒精溶液的浓度是一样的，100克酒精溶液中有30克酒精，说明原A管中200克酒精溶液含酒精：30×2=60（克），而且这60克的酒精全部来自某种浓度的酒精溶液．即说明倒入A管中的100克酒精溶液含酒精60克．所以，某种浓度的酒精溶液的浓度是60÷100×100%=60%．解答：解：B中酒精溶液的浓度是：（300+100）×2.5%÷100×100%=400×0.025÷100×100%=10%现在A中酒精溶液的浓度是：（200+100）×10%÷100×100%=300×0.1÷100×100%=30%最早倒入A中的酒精溶液浓度为：（100+100）×30%÷100=200×30%÷100=60%答：最早倒入A中的酒精溶液浓度为60%．故答案为：60．点评：不管是哪类的浓度问题，最关键的思维是要抓住题中没有变化的量，不管哪个试管中的酒精，都是来自最初的某种浓度的酒精溶液中，运用倒推的思维来解答．三．解答题（共8小题）7．浓度为95%的酒精600毫升中，加入多少水就能得到浓度为75%的消毒酒精？考点：浓度问题．专题：浓度与配比问题．分析：设加入x毫升水，根据混合前后纯酒精重量不变，列方程600×95%=75%×（600+x）解答即可．解答：解：设加入x毫升水，600×95%=75%×（600+x），450+0.75x=570，x=160；答：加入160毫升水就能得到浓度为75%的消毒酒精．点评：上述解法抓住了加水前后的溶液中溶质的质量没有改变这一关键条件，进行列式解答．8．甲乙两杯同样大，甲杯中盛有半杯清水，乙杯中盛满纯酒精，现将乙杯酒精倒入甲杯一半，搅匀后再将甲杯溶液的一半倒入乙杯．求此时乙杯酒精是溶液的几分之几？考点：浓度问题．专题：传统应用题专题．分析：先将乙杯中一半溶液倒入甲杯，则甲杯中的酒精浓度=100%÷2，再将甲杯中50%的酒精溶液的一半倒入乙杯，这时乙杯中的酒精含量=100%÷2÷2+100%÷2=75%；所以这时乙杯中的洒精浓度是75%．解答：解：100%÷2÷2+100%÷2，=25%+50%，=75%．答：这时乙杯中的酒精是溶液的75%．点评：此题考查学生有关浓度的问题，在解题时方法要灵活，构思要巧妙．9．有浓度为36%的溶液若干，加了一定量的水后，变成浓度为24%的溶液．如果一开始蒸发掉这么多的水，那么浓度变为多少？考点：浓度问题．专题：浓度与配比问题．分析：本题不知道溶液是多少，加了多少水不知道，所以设原来的溶液是x千克，加了y千克的水，根据溶质不变列出方程36%x=（x+y）×24%，解得：y=0.5x，当一开始蒸发掉这么多的水，求其浓度是利用溶质除以溶液=浓度即可．解答：解：设原来的溶液是x千克，加了y千克的水，由题意可得：36%x=（x+y）×24%3x=2x+2y3x﹣2x=2x+2y﹣2xx=2y所以：y=0.5x36%x÷（x﹣y）=0.36x÷（x﹣0.5x）=0.36x÷0.5x=72%答：如果一开始蒸发掉这么多的水，那么浓度变为72%．点评：解答本题的关键是舍而不求，本题无论怎么样变化，溶质始终没发生变化．10．有200克含盐率是10%的盐水，现在需要加水稀释成含盐率是5%的盐水，需要加水多少克？考点：浓度问题．专题：浓度与配比问题．分析：盐水在稀释前后的含盐量不变，所以抓住盐的质量不变这一关键条件来解答．浓度为10%的盐水200克，则盐的质量为200×10%=20（克），这20克盐占后来盐水的5%，后来盐水的质量为20÷5%=400（克），减去原来的盐水质量就是后来加进去的水的质量．解答：解：200×10%÷5%﹣200=20÷0.05﹣200=400﹣200=200（克）；答：需加水200克．点评：此题解答的关键是抓住稀释前后含盐量不变这一条件，求出后来盐水的质量，再减去原来盐水的质量，从而解决问题．11．有一杯300克的盐水，含盐率为8%，要使这杯盐水的含盐率为5%，应加入多少克水？考点：浓度问题．专题：浓度与配比问题．分析：盐水的重量是300克，浓度为8%，其中含盐量为300×8%=24（克）．加水后，含盐量不变，也就是在稀释后浓度为5%的盐水中，含盐量仍为24克，可知，稀释后的盐水重量为24÷5%=480（克）．原来300克的盐水，加水后变为480克，所以，加入的水位480﹣300=180（克）．解答：解：300×8%÷5%﹣300=24÷5%﹣300=480﹣300=180（克）．答：应加水180克．点评：解答此浓度问题要弄清下列关系式：溶液重量×浓度=溶质重量，溶质重量÷浓度=溶液重量．12．有若干克4%的盐水蒸发一些水分后变成了10%的盐水，再加进300克4%的盐水，混合变为6.4%的盐水，问最初的盐水是多少克？考点：浓度问题．专题：传统应用题专题．分析：运用逆推法，先运用十字相乘法求出10%的盐水的重量，进而求出10%的盐水中盐的重量；然后把最初的盐水的重量看成单位“1”，它的5%对应的数量是盐的重量，再用除法求出最初盐水的重量．解答：解：十字相乘法：4% 2%6.4%10% 2%；2%：2%=1：1；所以4%的盐水的重量和10%的盐水的重量相等，都是300克；300×10%=30（克）；30÷4%=750（克）；答：最初的盐水时750克．点评：十字交叉法是浓度计算的一个重要方法：如果题目中给出两个平行的情况A，B，满足条件a，b，然后A和B按照某种条件混合在一起形成的情况C，满足条件c，而且可以表示成：A•a+B•b=（A+B）•c=C•c．那么此时就可以用十字交叉法，表示如下：13．一个容器内装有12升纯酒精，倒出3升后，用水加满，再倒出6升，再用水加满，然后倒出9升，再用水加满，求这时容器内的酒精溶液的浓度是多少？考点：浓度问题．专题：浓度与配比问题．分析：12升纯酒精，倒出3升后，剩余12﹣3=9升9升酒精及水共12升液体，倒出6升，此时酒精剩余9﹣×6=4.5升再加满后，再倒出9升，此时酒精剩余：（4.5÷12）×（12﹣9）=1.125（升）；这是酒精溶液浓度为：1.125÷12×100%=9.375%，据此解答即可．解答：解：倒出3升后，剩纯酒精：12﹣3=9（升）；再倒出6升，剩纯酒精：（9÷12）×（12﹣6）=4.5（升）；再倒出9升，剩纯酒精：（4.5÷12）×（12﹣9）=1.125（升）这时容器内的溶液的浓度是：1.125÷12×100%=9.375%．答：这时容器内的酒精溶液浓度是9.375%．点评：此题关键是要分别求出每一次倒出后的纯酒精，然后根据溶液浓度=×100%计算出．14．A容器中有浓度4%的盐水330克，B容器中有浓度7%的盐水120克，从A倒180克到B，B容器中盐水浓度是多少？考点：浓度问题．专题：分数百分数应用题．分析：从A倒180克到B，B容器中盐水含盐量是180×4%+120×7%，B容器中盐水的质量为180+120=300克，利用盐水浓度=含盐量÷盐水的质量，据此解答即可．解答：解：从A倒180克到B，B容器中盐水含盐量是180×4%+120×7%=7.2+8.4=15.6（克）容器中盐水的质量为：180+120=300（克）15.6÷300=5.2%答：B容器中盐水浓度是5.2%．点评：解答本题的关键是求出从A倒180克到B，B容器中盐水含盐量．B档（提升精练）一．选择题（共10小题）1．有甲、乙、丙三种盐水，按甲与乙数量比为2：1混合，得到浓度为12%的盐水，按甲与乙的数量之比为1：2混合得到14%的盐水，如果甲、乙、丙数量的比为1：1：3混合成的盐水为10.2%，那么丙的浓度为（）A．7%B．8%C．9%D．7.5%考点：浓度问题．分析：根据：“按甲与乙的数量之比为2：1混合”，“按甲与乙的数量之比1：2混合”，“按甲、乙、丙的数量之比1：1：3混合”．从上面的条件中我们发现，只要使前两次操作得到的12%的盐水与14%的盐水重量相等，就可以使12%的盐水与14%的盐水混合，得到浓度为（12%+14%）÷2=13%的盐水，这种盐水里的甲和乙的数量比为1：1．现在我们要用这样的盐水与盐水丙按2：3混合，得到浓度为10.2%的盐水，13%﹣10.2%=2.8%，这样2份的13%的盐水就多了5.6%，这5.6%正好补全了丙盐水与10.2%的盐水的差距，5.6%÷3≈1.87%，10.2%﹣1.87%=8.33%，所以丙盐水的浓度为8.33%．解答：解：（12%+14%）÷2，=13%；（13%﹣10.2%）×2，=5.6%；10.2%﹣5.6%÷3，≈10.2%﹣1.87%，=8.33%．答：丙盐水的浓度约为8.33%．故选：B．点评：解答此题的关键是求甲、乙两种等量盐水混合后的浓度．2．在浓度30%的盐水中加入100克水，浓度降到20%，再加入（）克盐，浓度会恢复30%．A．约43克B．约30克C．约10克D．约23克考点：浓度问题．专题：传统应用题专题．分析：要变回30%的盐水，浓度不变，相当于后加入的盐和之前的100克水混合也是30%的盐水，含100克水的30%盐水，应该一共有100÷（1﹣30%）=（克），盐为﹣100≈43（克）解答：解：100÷（1﹣30%）﹣100=﹣100≈43（克）答：再加入43克盐，浓度会恢复30%．故选：A．点评：本题主要考查了浓度问题中稀释和加浓的知识点．3．把20克的盐放入100克水，盐与水的比是（）A．1：6B．1：5C．20：100考点：浓度问题．分析：要求“盐与水的比是多少”，必须知道盐和水的质量，此题已经给出，所以用盐的质量：水的质量即可．解答：解：20：100=1：5．故选：B．点评：此题考查了有关浓度问题，要审清题意．4．（•恩施州）把浓度为20%、30%、40%的三种盐水按2：3：5的比例混合在一起，得到的盐水浓度为（）A．32%B．33%C．34%D．35%考点：浓度问题．专题：浓度与配比问题．分析：由题意可知混合前后三种溶液盐水质量没有改变，以及混合前后三种溶液所含盐质量之和也没有改变，再由浓度为20%、30%、40%的三种盐水按2：3：5的比例混合在一起，可以把20%的盐水看作2，30%的盐水看作3，40%的盐水看作5，再根据混合后盐水浓度=三种溶液所含盐质量之和÷三种溶液盐水总质量×100%，解答出来即可．解答：解：（20%×2+30%×3+40%×5）÷（2+3+5）×100%=（0.4+0.9+2）÷10×100%=3.3÷10×100%=33%，答：得到的盐水浓度为33%，故选：B．点评：上述解法抓住了混合前后三种溶液盐水质量没有改变，以及混合前后三种溶液所含盐质量之和也没有改变这一关键条件，进行列式解答．5．现有浓度15%的糖水80克，要把它变成浓度为32%的糖水，需加糖（）克．A．100B．20C．13.6D．88考点：浓度问题．分析：糖水的浓度=，那么80克糖水中已经含有糖80×15%=12克，设还需要加入x克糖，根据题意即可得出：=32%，由此即可解得x的值，从而进行选择．解答：解：设还需要加入x克的糖，根据题意可得：=32%，=32%，25.6+0.32x=12+x，0.68x=13.6，x=20，所以还需要加20克的糖，故选：B．点评：此题考查了公式：糖水的浓度=在解决实际问题时的灵活应用，此类题目的方法是计算得出正确答案然后进行选择．6．在浓度为16%的40千克盐水中，蒸发（）水后可将浓度提高到20%．A．8千克B．9千克C．16千克D．4千克考点：浓度问题．专题：浓度与配比问题．分析：用40千克减去浓度是20%的盐水的盐水的重量，就是应蒸发掉水的重量．因盐的重量不变，含盐20%的盐水中的盐等于含盐16%的盐水中的盐，既（40×16%）千克，含盐20%的盐水的重量就是（40×16%÷20%）千克，据此解答．解答：解：40﹣40×16%÷20%，=40﹣32，=8（千克）；答：蒸发8千克水后可将浓度提高到20%．故答案为：A．点评：本题的关键是让学生理解浓度提高后，减少的是水的重量，盐的重量不变．7．甲、乙两只相同的水杯，甲杯50克糖水中含糖5克；乙杯中先放入2克糖，再放入20克水，搅匀后，（）中的糖水甜些．A．甲杯B．乙杯C．一样甜考点：浓度问题．分析：根据甲杯50克糖水中含糖5克，求出甲杯糖水的浓度（×100%）；根据乙杯中先放入2克糖，再放入20克水，可知形成22克的糖水，再求出乙杯糖水的浓度，进一步得解．解答：解：甲杯糖水的浓度：×100%=10%；乙杯糖水的浓度：×100%≈9.1%；10%＞9.1%，甲杯中的糖水甜些．故选：A．点评：关键是分别求出两杯糖水的浓度，再比较浓度的大小，进一步选出哪杯中的糖水甜些．8．从装满100克20%的盐水中倒出50克盐水后，在用清水将杯加满，搅拌后再倒出50克盐水，然后再用清水将杯加满．如此反复三次，杯中盐水的浓度是（）A．2%B．2.5%C．3%D．3.5%考点：浓度问题．专题：浓度与配比问题．分析：第一次倒出50克盐水后，盐还有（100﹣50）×20%=10克，所以第一次加满后杯中盐水浓度是10÷100=10%；同理，第二次倒出50克盐水后，盐还有（100﹣50）×10%=5克，第二次加满后杯中盐水浓度是5÷100=5%；第三次倒出50克盐水后，盐还有（100﹣50）×5%=2.5克，第三次加满后杯中盐水浓度是2.5÷100=2.5%．解答：解：第一次倒出50克盐水后盐水浓度：（100﹣50）×20%÷100=50×20%÷100=10÷100=10%第二次倒出50克盐水后盐水浓度：（100﹣50）×10%÷100=50×10%÷100=5÷100=5%第三次倒出50克盐水后盐水浓度：（100﹣50）×5%÷100=50×5%÷100=25÷100=2.5%答：杯中盐水的浓度是2.5%故选：B．点评：此题也可这样解答，每次倒出的盐水质量相同，并且都是上一次盐水质量的一半，因此，浓度就是上一次的一半，因此第三次加满后杯中盐水浓度是20÷2÷2÷2=25%．9．现在有果汁含量为40%的饮料600ml，要把它变成果汁含量为25%的饮料，需要加水（）ml．A．400B．240C．360D．100考点：浓度问题．分析：根据一个数乘分数的意义，先用“600×40%”计算出600ml果汁饮料中含有果汁的重量是240ml，进而根据“果汁含量不变”，得出后来果汁含量为25%的饮料的果汁含量是240ml；根据已知一个数的几分之几是多少，求这个数，用除法计算出后来果汁饮料的重量，继而用“后来果汁饮料的重量﹣原来果汁饮料的重量”解答即可．解答：解：果汁含量：600×40%=240（ml），后来果汁饮料的重量：240÷25%=960（ml），需要加水：960﹣600=360（ml），答：需要加水360ml．故选：C．点评：解答此题的关键：抓住不变量，即果汁含量不变，进行分析，解答，得出结论．10．2011年4月29日，英国威廉王子大婚，到场的各国政要多达1900人，盛况空前．在婚宴上，调酒师为宾客准备了一些酒精度为45%的鸡尾酒，大受赞赏．唯独有2位酒量不佳的宾客，一位在酒里加入一定量的汽水稀释成度数为36%才敢畅饮，另一位则更不济，加入2份同样多的汽水才敢饮用，这位不甚酒力者喝的是度数为（）的鸡尾酒．A．28%B．25%C．40%D．30%考点：浓度问题．专题：传统应用题专题．分析：假设每杯酒有100克，则原来有纯酒精：100×45%=45克，则加入一定量的汽水后浓度为36%，则后来每杯酒有：45÷36%=125克，加入了：125﹣100=25克汽水，则另一位加入了：25×2=50克汽水，所以浓度为：45÷（100+25×2）=30%；由此解答即可．解答：解：假设每杯酒有100克，则原来有纯酒精：100×45%=45（克），则后来每杯酒有：45÷36%=125（克），加入了汽水：125﹣100=25（克）浓度为：45÷（100+25×2）=30%答：这位不甚酒力者喝的是度数为30%的鸡尾酒；故选：D．点评：此题属于浓度问题，抓住酒中酒精的质量没有改变，运用假设法，求出第一位宾客加入汽水的质量，是解答此题的关键．二．填空题（共10小题）11．（•张家港市模拟）浓度为70%和40%的酒各一种，现在要用这两种酒配制含酒精60%的酒300克，需要浓度70%的酒200克，浓度40%的酒100克．考点：浓度问题．专题：分数百分数应用专题．分析：设取70%的酒精x克，则取40%的酒精（300﹣x）克，根据一种浓度是70%，另一种浓度为40%，现在要配制成浓度为60%的洒精300克，可列方程求解．解答：解：设取70%的酒精x克，则取40%的酒精（300﹣x）克，则由题意得：70%x+（300﹣x）40%=300×60%，0.7x+120﹣0.4x=1800.3x=60x=200所以300﹣x=300﹣200=100（克）．答：需70%的酒精200克，40%的酒精100克．故答案为：200；100．点评：本题考查理解题意的能力，在配制过程中，溶质是不变的，所以以溶质做为等量关系可列方程求解．12．（•东莞）用浓度为2.5%的盐水800克制成浓度为4%的盐水，需要蒸发掉300克水．考点：浓度问题．专题：分数百分数应用专题．分析：含盐率是指盐占盐水的百分比，先把原来盐水的总重量看单位“1”，盐的重量占2%，由此用乘法求出盐的重量；。

第八讲浓度问题应用题答案
1、有浓度为30%的酒精若干，添加了一定数量的水后稀释成浓度为24%的酒精溶液。

如果再加入同样多的水，那么酒精溶液的浓度变为多少？
2、有浓度为7%的盐水600克，要使盐水的浓度加大到10%，需要加盐多少克？
3、在浓度为50%的硫酸溶液100千克中，再加入多少千克浓度为5%的硫酸溶液，就可以配制成浓度为25%的硫酸溶液？
4、从装满100克浓度为80%的盐水杯中倒出40克盐水，再用浅水将杯加满倒出40克盐水，然后再用浅水将杯加满，如此反复三次后，杯中盐水的浓度是多少？
5、水果仓库运来含水量为90%的一种水果400千克。

一周后再测，发现含水量降低为80%，现在这批水果的总重量是多少千克？
6、有
A、B、C三根管子，A管以每秒4克的流量流出含盐20%的盐水，B管以每秒6克的流量流出含盐15%的盐水，C管以每秒10克的流量流出水，但C管打开后开始2秒不流，接着流5秒，然后又停2秒，再流5秒……现三管同时打开，1分钟后都关上。

这时得到的混合溶液中含盐百分之几？
1/ 1。