第二章拉伸与压缩
- 格式:doc
- 大小:3.88 MB
- 文档页数:6
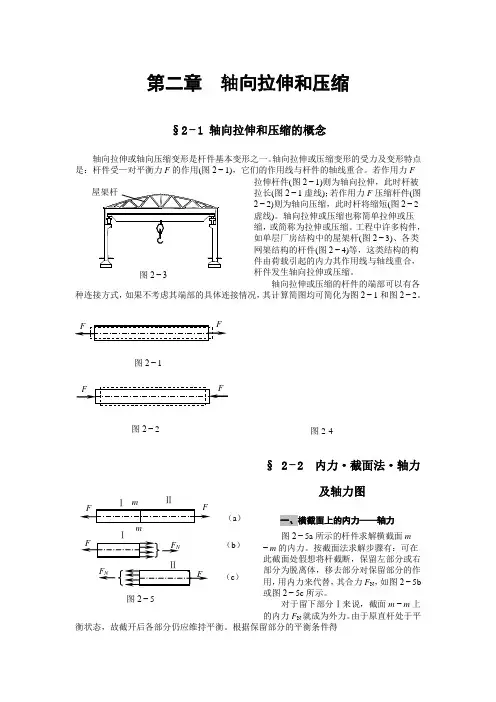
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸,此时杆被2−1虚线);若作用力F 压缩杆件(图(图2−2工程中许多构件,(图2−3)、各类(图2−4)等,这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有:可在此截面处假想将杆截断,保留左部分或右部分为脱离体,移去部分对保留部分的作用,用内力来代替,其合力F N ,如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说,截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态,故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N(a )(b ) (c )图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中,F N 为杆件任一截面m −m 上的内力,其作用线也与杆的轴线重合,即垂直于横截面并通过其形心,故称这种内力为轴力,用符号F N 表示。
若取部分Ⅱ为脱离体,则由作用与反作用原理可知,部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。
同样也可以从脱离体的平衡条件来确定。
二、轴力图当杆受多个轴向外力作用时,如图2−7a ,求轴力时须分段进行,因为AB 段的轴力与BC 段的轴力不相同。
要求AB 段杆内某截面m −m 的轴力,则假想用一平面沿m −m 处将杆截开,设取左段为脱离体(图2−7b),以F N Ⅰ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 F F -=ⅠN负号表示的方向与所设的方向相反,即为压力。
要求B C 段杆内某截面n-n 的轴力,则在n −n 处将杆截开,仍取左段为脱离体(图2−7c ),以F N Ⅱ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时,由于各段杆轴力的大小及正负号各异,所以为了形象地表明各截面轴力的变化情况,通常将其绘成“轴力图”(图2−7d)。





第2章 杆件的拉伸与压缩提要:轴向拉压是构件的基本受力形式之一,要对其进行分析,首先需要计算内力,在本章介绍了计算内力的基本方法——截面法。
为了判断材料是否会发生破坏,还必须了解内力在截面上的分布状况,即应力。
由试验观察得到的现象做出平面假设,进而得出横截面上的正应力计算公式。
根据有些构件受轴力作用后破坏形式是沿斜截面断裂,进一步讨论斜截面上的应力计算公式。
为了保证构件的安全工作,需要满足强度条件,根据强度条件可以进行强度校核,也可以选择截面尺寸或者计算容许荷载。
本章还研究了轴向拉压杆的变形计算,一个目的是分析拉压杆的刚度问题,另一个目的就是为解决超静定问题做准备,因为超静定结构必须借助于结构的变形协调关系所建立的补充方程,才能求出全部未知力。
在超静定问题中还介绍了温度应力和装配应力的概念及计算。
不同的材料具有不同的力学性能,本章介绍了塑性材料和脆性材料的典型代表低碳钢和铸铁在拉伸和压缩时的力学性能。
2.1 轴向拉伸和压缩的概念在实际工程中,承受轴向拉伸或压缩的构件是相当多的,例如起吊重物的钢索、桁架第2章 杆件的拉伸与压缩 ·9··9·2.2 拉(压)杆的内力计算2.2.1 轴力的概念为了进行拉(压)杆的强度计算,必须首先研究杆件横截面上的内力,然后分析横截面上的应力。
下面讨论杆件横截面上内力的计算。
取一直杆,在它两端施加一对大小相等、方向相反、作用线与直杆轴线相重合的外力,使其产生轴向拉伸变形,如图2.2(a)所示。
为了显示拉杆横截面上的内力,取横截面把m m −拉杆分成两段。
杆件横截面上的内力是一个分布力系,其合力为N F ,如图2.2(b)和2.2(c)所示。
由于外力P 的作用线与杆轴线相重合,所以N F 的作用线也与杆轴线相重合,故称N F 为轴力(axial force)。
由左段的静力平衡条件0X =∑有:()0+−=N F P ,得=N F P 。





第二章 拉伸与压缩一、是非题2-1 、当作用于杆件两端的一对外力等值反向共线时则杆件产生轴向拉伸或压缩变形。
( ) 2-2 、关于轴力有下列几种说法:1、轴力是作用于杆件轴线上的载荷( )2、轴力是轴向拉伸或压缩时杆件横截面上分布内力系的合力( )3、轴力的大小与杆件的横截面面积有关( )4、轴力的大小与杆件的材料无关( )2-3、 同一材料制成的阶梯杆及其受力如图2-1CD 段的横截面面积为ABC 和DE 段均为2A 分别用和表示截面上的轴力和正应力则有 1、轴力321N N N F F F >> 。
( ) 2、正应力1σ>2σ>3σ。
( )2-4、 轴力越大,杆件越容易拉断,因此轴力的大小可以用来判断杆件的强度。
( )2-5 、一轴向拉伸的钢杆材料弹性模量E=200GP a ,比例极限p σ=200MP a ,今测得其轴向线应变ε=0.0015,则由胡克定律得其应力εσE ==300MP a 。
( ) 2-6 、关于材料的弹性模量E ,有下列几种说法: 1、E 的量纲与应力的量纲相同。
( ) 2、E 表示弹性变形能力的大小。
( ) 3、各种牌号钢材的E 值相差不大。
( ) 4、橡皮的E 比钢材的E 值要大。
( )5、从某材料制成的轴向拉伸试样,测的应力和相应的应变,即可求的其σ=E 。
( ) 2-7 、关于横向变形系数(泊松比)μ,有下列几种说法:1、为杆件轴向拉、压时,横向应变ε'与纵向应变ε之比的绝对值。
( )2、 μ值越大,其横向变形能力越差。
( )3、各种材料的μ值都满足:0<μ≤0.5。
( ) 2-8、 受轴向拉、压的等直杆,若其总伸长为零,则有 1、杆内各处的应变必为零。
( ) 2、杆内各点的位移必为零。
( ) 3、杆内各点的正应力必为零。
( )4、杆的轴力图面积代数和必为零。
( )2-9、 打入土内的木桩如图2-2沿轴线单位长度的摩擦力2ky f =(k 为常数),木桩横截面面积为A 弹性模量为E 则木桩总变形的计算式为()()EApl EAky y p EAdy y N l ll402=⋅-==∆⎰⎰。
( )2-10、 空心圆截面在弹性范围内进行压缩试验时,其外径增大,内径减小。
所以在同一截面上,内、外径处的径向线应变是反号的。
( ) 2-11、 图2-3示均质圆杆在自重作用下,若以mn V 和mn U 表示任意两横截面m -m 和n-n 之间的体积和弹性变形能则其变形能密度为mn mn V U u =。
上式也表示该部分内任意两点A 或B 处的变形能密度。
( )2-12、 轴向拉、压杆,若横截面上有应力,则杆件不一定有纵向变形和横向变形。
反之,杆件有变形,也不一定有应力。
( ) 二、选择题2-13、 轴向拉、压杆,由截面法求得同一截面的左右两部分的轴力则两轴力大小相等而( )。
A 、方向相同,符号相同; B 、方向相反,符号相同;C 、方向相同,符号相反;D 、方向相反,符号相反。
2-14、轴向拉、压杆横截面上正应力公式A N =σ的应用条件是( )。
A 、应力必须低于比例极限;B 、构件必须由同一材料制成;C 、构件截面形状只能是矩形或圆形;D 、构件必须是小变形;E 、构件必须是等截面直杆。
2-15 、轴向拉、压中的平面假设适用于( )。
A 、整根杆件长度的各处;B 、除杆件两端外的各处;C 、距杆件两端或集中载荷作用点稍远的各点处。
2-16、 影响杆件工作应力的因素有( );影响极限应力的因素有( );影响许用应力的因素有( )。
A 、载荷; B 、材料性质; C 、截面尺寸;D 、工作条件。
2-17、 两拉杆的材料和所受的拉力都相同,且处在弹性范围内,则1.若两杆的截面积相同,而长度1l >2l ,则两杆的伸长1l ∆( )2l ∆,纵向线应变1ε( )2ε。
2.若两杆长度相同,而截面积1A >2A ,则两杆的伸长1l ∆( )2l ∆,纵向线应变1ε( )2ε。
A 、 大于; B 、小于; C 、等于。
2-18、 图2-4所示的各结构中图(a )是( );图(b )是( );图(c )是( );图(d )是( );图(e )是( );图(f )是( )。
A 、 静定结构;B 、一次超静定;C 、二次超静定; D 、三次超静定。
2-19 、图示等截面直杆,两端固定,各杆段的材料相同。
正确的轴力图是( )。
A 、图(a ); B 、图(b ); C 、图(c )。
2-20 、在拉、压超静定的结构中,各组成部分的内力分配与( )有关。
A 、构件的强度;B 、构件的刚度;C 、构件的强度和刚度;D 、构件的几何形状。
2-21、在拉、压结构中,由于温度均匀变化,则( )。
A 、静定结构仅可能引起应力,不产生变形;超静定结构仅可能引起变形,不产生应力。
B 、 静定结构仅可能引起变形,不引起应力;超静定结构可能引起应力和变形。
C 、 任何结构都只可能引起变形,不产生应力。
D 、 任何结构都只可能引起应力和变形。
2-22、 在拉、压杆中的横截面尺寸急剧变化处,其理论应力集中系数为( )的比值。
A 、削弱截面上的平均应力与未削弱截面的平均应力。
B 、削弱截面上的最大应力与削弱截面的平均应力。
C 、削弱截面上的最大应力与未削弱截面的平均应力。
2-23 、材料、厚度、有效宽度B 均相同的三条橡皮带的受力情况如图2-6所示,当P 力逐渐增大时,( )首先拉断;( )最后拉断。
A 、 图(a )所示的橡皮带。
B 、图(b )所示的橡皮带。
C 、图(c )所示的橡皮带。
三、填空题2-24 、截面面积为A 的等直杆,其两端受轴向拉力P 时,最大正应力m a xσ=________,发生在________上,该截面上的剪应力τ=________,最大剪应力ma xτ=________,发生在=________上,该截面上的正应力σ=________;任意两个相互垂直的斜截面上的正应力之和都等于________。
答案 2-25、 图2-7示低碳钢拉伸时的应力---应变图,试在图中表明: 1、加载到d 点时的弹性应变e ε和塑性应变p ε; 2、延伸率δ;3、开始颈缩时的对应点e ;4、应力最大之的对应点f ;5、拉断时消耗的变形能密度p u 。
答案2-26、低碳钢在屈服阶段呈现应力________,应变________的现象;冷作硬化后,将使材料的比例极限________,而塑性________。
答案2-27、 对于________材料,通常以产生0.2%的________时所对应的________作为屈服极限,称为材料的屈服强度,并用记号________表示。
答案2-28、低碳钢在温度升高到300℃以后,随温度继续升高,则弹性模量E ________、屈服极限s σ________、强度极限b σ________、延伸率δ________;而在低温的情况下,低碳钢的强度________,而塑性________。
答案2-29、轴向拉伸杆件体积不变的条件是________。
答案2-30、 两根受轴向拉伸的杆件均处在弹性范围内,一为钢杆s E =210GP a ,另一为铸铁杆b E =100GP a 。
若两杆正应力相同,则两者纵向应变比值为________,若两者的纵向应变相同,则两者正应力的比值为________,变形能密度的比值为________。
答案2-31、 超静定结构是________超出独立的静力学平衡方程数目的结构,超静定结构由构件尺寸加工误差或支座沉陷将引起________,求解超静定结构的关键是建立________。
答案 四、问答题2-32 、将低碳钢拉伸图中的纵坐标P 、横坐标l ∆,分别除以原始横截面面积A 和工作长度l ,所得的应力-应变图,并没有反映试样横截面面积的减小,因而屈服强度s σ和强度极限b σ都不表示真实的极限应力,为什么可作为工程设计中的依据?答案2-33、由两种材料的试样,分别测得其延伸率为5δ=20%和10δ=20%,试问那种材料的塑性性能较好,为什么?答案2-34、已知轴向压缩时的最大剪应力发生在45的斜截面上,为什么铸铁压缩试验破坏时,不是沿45°而是大致沿55°斜截面剪断的?答案 2-35、常见电线杆拉索上的低压瓷质绝缘子如图2-8所示,试根据绝缘子的强度要求,比较图(a )和(b )两种结构的合理性。
答案 2-36、由同一材料制成的不同构件,其许用应力是否相同?一般情况下脆性材料的安全系数要比塑性材料的安全系数选得大些,为什么?答案2-37、混凝土压缩试验时,试验机压板与试样接触面间,涂润滑油与否,对试样破坏有何影响,对试验所得数据有否影响?答案2-38、 图2-9示结构中,杆1和2的许用应力、横截面积分别为[]1σ、1A 和[]2σ、2A ,则两杆的许用轴力分别为[]1N =[]1σ1A 和[]2N =[]2σ2A 。
试问能否由平衡条件(0=∑y )求得结构的许可载荷:[]P =[]1σ1A cos α+[]2σ2A cos β。
为什么?答案2-39、图2-10示结构中,已知载荷P ,杆长l 和拉杆BD 的许用应力[]σ,欲使BD 杆用料最省,试求夹角θ的合理值。
答案2-40、上题图2-10示结构中,若BC 和BD 杆的材料相同,且拉、压许用应力相等,则为使结构用料最省,试求夹角θ的合理值。
答案 2-41、若图2-10示结构中的两杆均为横截面积为A 的铸铁杆,且许用压应力为许用拉应力的三倍,试提出提高结构承载能力的简便方法。
答案2-42、试分别叙述胡克定律的两种表达式EANl l =∆和Eσε=的不同用途。
答案2-43、抗拉刚度为 EA 的拉杆AB ,其尺寸及受力情况如图2-11,在弹性范围内,试问下列算式是否正确?若不正确,写出其正确的表达式。
1.杆的总伸长 ()EAl P EAl P P l l l 2212121++=∆+∆=∆;2.杆总应变 221121l l l l ∆+∆=+=εεε;3.杆的总变形能()EAllPEAlPUUU22212212121++=+=。
答案2-44、已知圆管的内、外直径分别为d和D,厚度为t,弹性模量E,泊松比为μ和横截面上正应力为σ,试分别求其内、外直径厚度和内、外圆周长度的改变量,并比较它们的线应变值。
答案2-45、在图2-12示,杆件表面有一条斜直线AB,当杆件承受轴向拉伸时,试问该斜线是否做平行移动?答案2-46、简单托架,如图2-13a所示,在小变形条件下,为求节点B的位移,可设想将托架在节点B处拆开。
则CB杆变形后为1CB;DB杆变形后为DB2,然后分别做垂线B1B3和B2B3,使两杆相交于点B3,而由于一点的位移是矢量,则可以BB1和BB2为邻边,作平行四边形,从而求的总位移BB4(如图b)。