第二章拉伸压缩2拉伸压缩力学性能
- 格式:ppt
- 大小:9.38 MB
- 文档页数:24
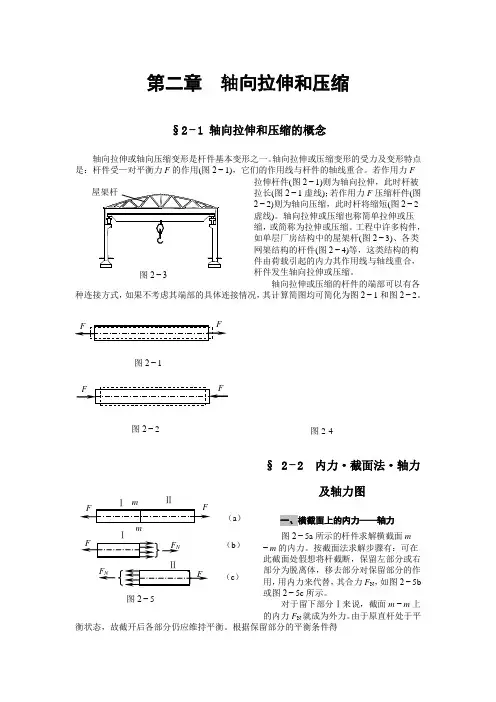
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸,此时杆被2−1虚线);若作用力F 压缩杆件(图(图2−2工程中许多构件,(图2−3)、各类(图2−4)等,这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有:可在此截面处假想将杆截断,保留左部分或右部分为脱离体,移去部分对保留部分的作用,用内力来代替,其合力F N ,如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说,截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态,故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N(a )(b ) (c )图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中,F N 为杆件任一截面m −m 上的内力,其作用线也与杆的轴线重合,即垂直于横截面并通过其形心,故称这种内力为轴力,用符号F N 表示。
若取部分Ⅱ为脱离体,则由作用与反作用原理可知,部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。
同样也可以从脱离体的平衡条件来确定。
二、轴力图当杆受多个轴向外力作用时,如图2−7a ,求轴力时须分段进行,因为AB 段的轴力与BC 段的轴力不相同。
要求AB 段杆内某截面m −m 的轴力,则假想用一平面沿m −m 处将杆截开,设取左段为脱离体(图2−7b),以F N Ⅰ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 F F -=ⅠN负号表示的方向与所设的方向相反,即为压力。
要求B C 段杆内某截面n-n 的轴力,则在n −n 处将杆截开,仍取左段为脱离体(图2−7c ),以F N Ⅱ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时,由于各段杆轴力的大小及正负号各异,所以为了形象地表明各截面轴力的变化情况,通常将其绘成“轴力图”(图2−7d)。










直杆轴向拉伸与压缩时的变形与应力分析和拉伸与压缩时材料的力学性能——教案第一章:直杆轴向拉伸与压缩的基本概念1.1 学习目标1. 了解直杆轴向拉伸与压缩的基本概念;2. 掌握直杆轴向拉伸与压缩的变形与应力分析方法。
1.2 教学内容1. 直杆轴向拉伸与压缩的定义;2. 直杆轴向拉伸与压缩的变形与应力分析方法。
1.3 教学活动1. 讲解直杆轴向拉伸与压缩的基本概念;2. 分析直杆轴向拉伸与压缩的变形与应力分析方法。
第二章:直杆轴向拉伸与压缩的变形分析2.1 学习目标1. 了解直杆轴向拉伸与压缩的变形规律;2. 掌握直杆轴向拉伸与压缩的变形分析方法。
2.2 教学内容1. 直杆轴向拉伸与压缩的变形规律;2. 直杆轴向拉伸与压缩的变形分析方法。
2.3 教学活动1. 讲解直杆轴向拉伸与压缩的变形规律;2. 分析直杆轴向拉伸与压缩的变形分析方法。
3.1 学习目标1. 了解直杆轴向拉伸与压缩的应力分布;2. 掌握直杆轴向拉伸与压缩的应力分析方法。
3.2 教学内容1. 直杆轴向拉伸与压缩的应力分布;2. 直杆轴向拉伸与压缩的应力分析方法。
3.3 教学活动1. 讲解直杆轴向拉伸与压缩的应力分布;2. 分析直杆轴向拉伸与压缩的应力分析方法。
第四章:拉伸与压缩时材料的力学性能4.1 学习目标1. 了解拉伸与压缩时材料的力学性能指标;2. 掌握拉伸与压缩时材料的力学性能分析方法。
4.2 教学内容1. 拉伸与压缩时材料的力学性能指标;2. 拉伸与压缩时材料的力学性能分析方法。
4.3 教学活动1. 讲解拉伸与压缩时材料的力学性能指标;2. 分析拉伸与压缩时材料的力学性能分析方法。
第五章:实例分析与应用5.1 学习目标2. 能够应用所学知识解决实际问题。
5.2 教学内容1. 直杆轴向拉伸与压缩的实例分析;2. 应用所学知识解决实际问题。
5.3 教学活动1. 分析直杆轴向拉伸与压缩的实例;2. 解决实际问题,巩固所学知识。
第六章:弹性模量的概念与应用6.1 学习目标1. 理解弹性模量的定义及其物理意义;2. 掌握弹性模量在材料力学中的应用。
025材料在拉伸和压缩时的力学性能解析材料在拉伸和压缩时的力学性能是指材料在外力作用下的变形和破坏行为。
这些性能参数包括弹性模量、屈服强度、延伸率、断裂强度等,这些性能参数反映了材料在受力过程中的力学行为。
材料在拉伸和压缩时的力学性能可以通过应力-应变曲线来分析。
应力-应变曲线可以描述材料在受力作用下的应变和应力之间的关系。
根据应力-应变曲线的不同形状,可以得到不同的力学性能。
材料在拉伸时的力学性能:1. 弹性模量(Young's modulus):弹性模量是指材料在拉伸过程中的应变与应力之间的比例关系。
弹性模量越大,材料的刚度越高,抗拉性能越好。
2. 屈服强度(Yield strength):屈服强度是指材料开始发生塑性变形的应力值。
材料的屈服强度越高,具有越好的抗拉性能。
3. 延伸率(Elongation):延伸率是指材料在拉伸过程中的长度增加量与原始长度之比。
延伸率越高,材料的延展性越好。
4. 断裂强度(Tensile strength):断裂强度是指材料在拉伸过程中的最大应力值。
断裂强度越高,材料的抗拉性能越好。
材料在压缩时的力学性能:需要注意的是,材料在拉伸和压缩时的力学性能往往不完全对称。
在一些材料中,其拉伸性能表现较好,而压缩性能较差,或者压缩性能表现较好,而拉伸性能较差。
因此,在设计工程结构和选择材料时,需要综合考虑材料在拉伸和压缩时的力学性能。
总之,材料在拉伸和压缩时的力学性能对于材料的应用和工程设计具有重要影响。
通过分析材料的弹性模量、屈服强度、延伸率、断裂强度等性能参数,可以更好地了解材料的力学行为,为材料选择和工程设计提供指导和参考。
《工程力学II 》拉伸与压缩实验指导书§1 拉伸实验指导书1、概述常温、静载作用下的轴向拉伸实验是测量材料力学性能中最基本、应用最广泛的实验。
通过拉伸实验,可以全面地测定材料的力学性能,如弹性、塑性、强度、断裂等力学性能指标。
这些性能指标对材料力学的分析计算、工程设计、选择材料和新材料开发都有极其重要的作用。
2、实验目的2.1 测定低碳钢的下列性能指标:两个强度指标:流动极限s σ、强度极限b σ; 两个塑性指标:断后伸长率δ、断面收缩率ϕ;测定铸铁的强度极限b σ。
2.2观察上述两种材料在拉伸过程的各种实验现象,并绘制拉伸实验的F -l ∆曲线。
2.3分析比较低碳钢(典型塑性材料)和铸铁(典型脆性材料)的力学性能特点与试样破坏特征。
2.4了解实验设备的构造和工作原理,掌握其使用方法。
2.5了解名义应力应变曲线与真实应力应变曲线的区别,并估算试件断裂时的应力k σ。
3、实验原理对一确定形状试件两端施加轴向拉力,使有效部分为单轴拉伸状态,直至试件拉断,在实验过程中通过测量试件所受荷载及变形的关系曲线并观察试件的破坏特征,依据一定的计算及判定准则,可以得到反映材料拉伸试验的力学指标,并以此指标来判定材料的性质。
为便于比较,选用直径为10mm 的典型的塑性材料低碳钢Q235及典型的脆性材料灰铸铁HT150标准试件进行对比实验。
常用的试件形状如图1.1所示,实验前在试件标距范围内有均匀的等分线。
典型的低碳钢(Q235)的L F ∆-曲线和灰口铸铁(HT150)的L F ∆-曲线如图1.2、图1.3所示。
图1.2 低碳钢拉伸L F ∆-曲线 图1.3 铸铁拉伸L F ∆-曲线 F p -比例伸长荷载;F e -弹性伸长荷载;F su -上屈服荷载; F b -极限荷载F sl -下屈服荷载;F b -极限荷载;F k -断裂荷载图1.1常用拉伸试件形状低碳钢Q235试件的断口形状如图1.4所示,铸铁HT150试件的断口形状如图1.5所示,观察低碳钢的L F ∆-曲线,并结合受力过程中试件的变形,可明显地将其分为四个阶段:弹性阶段、屈服阶段、强化阶段、局部变形阶段。