当前位置：文档之家 › 材料力学第二章拉伸与压缩下共67页文档

材料力学第二章拉伸与压缩下共67页文档

  • 格式：ppt
  • 大小：4.18 MB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

材料力学(机械类)第二章 轴向拉伸与压缩

材料力学(机械类)第二章 轴向拉伸与压缩

第
二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1

轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下，杆件伸长 （简称拉伸） 轴向压缩——轴力作用下，杆件缩短 （简称压缩）

2
拉、压的特点：

1.两端受力——沿轴线，大小相等，方向相反 2. 变形—— 沿轴线
3

§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN，求刚索的应力和 C点的垂直位移。 （刚索的 E =177GPa，设横梁ABCD为刚梁）
16
§2-4

材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。

现在要研究材料的整个力学性能（应力 —— 应变）：
从受力很小
破坏
理论上——用简单描述复杂
工程上——为（材料组成的）构件当好医生
17
一、 低碳钢拉伸时的力学性能 （含碳量<0.3%的碳素钢）
力均匀分布于横截面上，σ等于常量。于是有：
N d A d A A
A A
得应力：

N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
第二章_直杆的拉伸和压缩

第二章_直杆的拉伸和压缩


F
1
FN1 A1
28.3103 202 106
4
90106 Pa 90MPa
2
FN2 A2
20103 152 106
89106Pa 89MPa
2.1.3 应变的概念
绝对变形ΔL， 相对变形或线应变：
L
L
伸长时ε为正，缩短时ε为负
2.2 拉伸和压缩时材料的力学性能
2.2.1 拉伸和压缩试验及材料的力学性能
1、强度校核：
max
N A
2、设计截面：
A
N
3、确定许可载荷： NA
目录
塑性材料 ：以材料的屈服极限作为确定许用应力的基础。 变形特征：当杆内的最大工作应力达到材料的屈服极限时，沿 整个杆的横截面将同时发生塑性变形，影响杆的正常工作。 许 用内力的表示为：
对于一般构件的设计，ns规定为1.5到2.0 脆性材料 ：以材料的断裂极限作为确定许用应力的基础。 变形特征：直到拉断也不发生明显的塑性变形，而且只有断裂 时才丧失工作能力。许用内力的表示为：
OA
BC
D
PA
PB
PC
PD
N1 A
BC
D
PA
PB
PC
PD
解： 求OA段内力N1：设置截面如图
X 0 N 1 P A P B P C P D 0
N 1 5 P 8 P 4 P P 0N1 2P
N2
BC
D
PB 同理，求得AB、BC、 CD段内力分别为：
N2= –3P N3= 5P N4= P
2.1.3 拉伸和压缩时横截面上的应力
FN F
AA
应力集中：在截面突变处应力局部增大的 现象
应力集中系数：k=σmax/σ
材料力学 第二章 轴向拉伸和压缩.

材料力学 第二章 轴向拉伸和压缩.


4. 公式的应用条件： 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 5. Saint-Venant原理： 离开载荷作用处一定距离，应力分布与大小不受外载荷
作用方式的影响。
6. 应力集中（Stress Concentration）： 在截面尺寸突变处，应力急剧变大。
20
Saint-Venant原理与应力集中示意图
0 (1cos2 ) 2 或: 0 sin 2 2

图3

x
33
[例6] 直径为d =1 cm 杆受拉力P =10 kN的作用，试求最大剪应 力，并求与横截面夹角30°的斜截面上的正应力和剪应力。 解：拉压杆斜截面上的应力，直接由公式求之：
N P0
PN
2. 轴力——轴向拉压杆的内力，用N 表示。
9
3. 轴力的正负规定:
N 与外法线同向,为正轴力(拉力) N与外法线反向,为负轴力(压力)
N
N
N
N
N>0 N<0
三、 轴力图—— N (x) 的图象表示。 ①反映出轴力与横截面位置变化关系，较直观； 意 ②确定出最大轴力的数值 义 及其所在横截面的位置，
②代替：任取一部分，其弃去部分对留下部分的作用，用作用 在截开面上相应的内力（力或力偶）代替。
③平衡：对留下的部分建立平衡方程，根据其上的已知外力来
计算杆在截开面上的未知内力（此时截开面上的内力 对所留部分而言是外力）。
8
例如： 截面法求N。 P
A
A 简图
P
截开： P P
P N
代替： 平衡：
A
x
X 0
P600 A /(cos 600 sin 600 ) 4 50 102 4 / 3 46.2kN
材料力学课件第二章 轴向拉伸和压缩

材料力学课件第二章 轴向拉伸和压缩


2.3 材料在拉伸和压缩时的力学性能
解： 量得a点的应力、应变分别 为230MPa、0.003
E=σa/εa=76.7GPa 比例极限σp=σa=230MPa 当应力增加到σ＝350MPa时，对应b点，量得正应变值
ε = 0. 0075 过ｂ点作直线段的平行线交于ε坐标轴，量得 此时的塑性应变和弹性应变
εp=0. 0030 εe= 0 . 0075-0.003=0.0045
内力：变形固体在受到外力作用 时，变形固体内部各相邻部分之 间的相互作用力的改变量。
①②③ 切加求 一内平 刀力衡
应力:是内力分布集度，即 单位面积上的内力
p＝dF/dA
F
F
FX = 0
金属材料拉伸时的力学性能
低碳钢(C≤0.3%)
Ⅰ 弹性阶段σe σP=Eε
Ⅱ 屈服阶段 屈服强度σs 、（σ0.2）
FN FN<0
2.2 拉压杆截面上的内力和应力
第二章 轴向拉伸和压缩
在应用截面法时应注意：
（1）外载荷不能沿其作用线移动。
2.2 拉压杆截面上的内力和应力
第二章 轴向拉伸和压缩
在应用截面法时应注意：
（2）截面不能切在外载荷作用点处，要离开或 稍微离开作用点。
1
2
11
22
f 30 f 20
60kN
Ⅲ 强化阶段 抗压强度 （强度极限）σb
Ⅳ 局部颈缩阶段
例1
一根材料为Q235钢的拉伸试样，其直径d＝10mm，工作段 长度l＝100mm。当试验机上荷载读数达到F＝10kN 时，量 得工作段的伸长为Δ l＝0.0607mm ，直径的缩小为 Δd=0.0017mm 。试求此时试样横截面上的正应力σ，并求出 材料的弹性模量Ｅ。已知Q235钢的比例极限为σ p ＝200MPa。
材料力学第2章拉伸压缩与剪切

材料力学第2章拉伸压缩与剪切


A
5倍试样： l = 5 .65 A
l
10倍试样： l = 11 .3 A
2- 16
8
3. 试验仪器：万能材料试验机
2- 17
M L
二、低碳钢拉伸时的力学性能 (a) 低碳钢试件 的拉伸图(P-êL图)
(b) 低碳钢试件 的应力--应变曲 线(σ --ε 图)
2- 18
9
1. 弹性阶段 (OA段) (1)OA' -- 比例段: A A' σp -- 比例极限
M L
§2-4 材料在拉伸时的机械性能 机械性能：也称力学性能
一、试验条件及实验仪器 是指材料在外力作用下表 现出的变形、破坏等方面 的特性。
1. 试验条件：常温(20℃) 静载（及缓慢地加载） 2. 标准试件 标准圆截面试件:
d
5倍试样： l = 5d
10 倍试样： l = 10 d
l
标准矩形截面试件:
变形前
2° 横线保持为直线，并 与纵线垂直。 平面假设：原为平面的横 P 截面在变形后仍为平面， 且仍垂直于轴线。
P
变形后
P
σ
}
结论：正应力σ均匀分布在 横截面上。 FN=P
∴ σ =
FN A
29
M L
2- 10
5
四、圣维南(Saint-Venant)原理 在静力等效的条件下，不同的加载方式只对加载处附 近区域的应力分布有影响，而对远离加载处较远部分的应 力分布并没有显著的影响。 P P
FN 1 sin 37o − P = 0 ∑Fy=0，
∴FN 1 = 5 P 3
FN 2 = 4 P 3
FN1 370 FN2
2º 由强度条件求许可载荷[P] 由杆①强度条件得 P F σ 1 = N 1 ≤ [σ ]1 ∴ FN1 ≤ A1[σ ]1 即 5 P ≤ A1[σ ]1 ∴ P ≤ 96KN （1） A1 3 由杆②强度条件得
材料力学 第2章轴向拉伸与压缩

材料力学 第2章轴向拉伸与压缩

15mm×15mm的方截面杆。
A
FN128.3kN FN220kN
1
（2）计算各杆件的应力。
C
45°
2
B
s AB

FN 1 A1

28.3103
202
M
Pa90MPa
4
F
FN 1
F N 2 45°
y
Bx
s BC

FN 2 A2
21052103MPa89MPa
F
§2.4 材料在拉伸和压缩时的力学性能
22
5 圣维南原理
s FN A
（2-1）
（1）问题的提出
公式（2-1）的适用范围表明：公式不适用于集中力作
用点附近的区域。因为作用点附近横截面上的应力分布是非
均匀的。随着加载方式的不同。这点附近的应力分布方式就
会发生变化。 理论和实践研究表明：
不同的加力方式，只对力作
用点附近区域的应力分布有
显著影响，而在距力作用点
力学性能：指材料从开始受力至断裂的全部过程中，所表 现出的有关变形和破坏的特性和规律。
材料力学性能一般由试验测定，以数据的形式表达。 一、试验条件及试验仪器 1、试验条件：常温(20℃)；静载（缓慢地加载）；
2、标准试件：常用d=10mm，l=100 mm的试件
d
l
l =10d 或 l = 5d
36
b点是弹性阶段的最高点.
σe—
oa段为直线段，材料满足 胡克定律
sE
sp
E
se sp
s
f ab
Etana s
O
f′h
反映材料抵抗弹
性变形的能力.
40
材料力学--轴向拉伸和压缩

材料力学--轴向拉伸和压缩


2、轴力图的作法：以平行于杆轴线的横坐标（称为基
线）表示横截面的位置；以垂直于杆轴线方向的纵坐
标表示相应横截面上的轴力值，绘制各横截面上的轴 FN
力变化曲线。
x
§2-2 轴力、轴力图
三、轴力图
FN
3、轴力图的作图步骤：
x
①先画基线（横坐标x轴），基线‖轴线；
②画纵坐标，正、负轴力各绘在基线的一侧；
③标注正负号、各控制截面处 、单位及图形名称。
FN
4、作轴力图的注意事项： ①基线一定平行于杆的轴线，轴力图与原图上下截面对齐； ②正负分绘两侧， “拉在上，压在下”，封闭图形； ③正负号标注在图形内，图形上下方相应的地方只标注轴力绝对值，不带正负号； ④整个轴力图比例一致。
50kN 50kN 50kN
第二章 轴向拉伸和压缩
第二章
轴向拉伸和压缩
第二章 轴向拉伸和压缩
§2 — 1 概述
§2 — 2 轴力 轴力图
目
§2 — 3 拉（压）杆截面上的应力
§2 — 4 拉（压）杆的变形 胡克定律 泊松比
录
§2 — 5 材料在拉伸与压缩时的力学性质
§2 — 6 拉（压）杆的强度计算
§2 — 7 拉（压）杆超静定问题
FN
作轴力图的注意事项： ①多力作用时要分段求解，一律先假定为正方向，优先考虑直接法； ②基线‖轴线，正负分绘两侧， “拉在上，压在下”，比例一致，封闭图形； ③正负号标注在图形内，图形上下方相应的地方只标注轴力绝对值，不带正负号； ④阴影线一定垂直于基线，阴影线可画可不画。
§ 2-3拉（压）杆截面上的应力
§2 — 8 连接件的实用计算
§2-1 概述 §2-1 概述
——轴向拉伸或压缩，简称为拉伸或压缩，是最简单也是做基本的变形。
材料力学第二章-轴向拉伸与压缩

材料力学第二章-轴向拉伸与压缩

FN 3 P
1
2
P
P
1
2
FN1
3 P
3
P FN2
PP FN3
FN 1 P FN 2 0 FN 3 P
1
2
4、作内力图
P
P
P
3 P
1 FN
P
2
3
P x
[例2] 图示杆旳A、B、C、D点分别作用着大小为5P、8P、 4P、 P 旳力，方向如图，试画出杆旳轴力图。
OA PA
B PB
C PC
D PD
q
u 正应力旳正负号要求：
sx
sx sx
s
x
P
u 对变截面杆， 当截面变化缓慢时，横截面上旳 正应力也近似为均匀分布，可有：
s (x) FN (x)
A( x)
合力作用线必须与杆件轴线重叠；
圣维南原理
若用与外力系静力等 效旳合力替代原力系， 则这种替代对构件内应 力与应变旳影响只限于 原力系作用区域附近很 小旳范围内。 对于杆件，此范围相当 于横向尺寸旳1～1.5倍。
h
解： 1） BD杆内力N
取AC为研究对象，受力分析如图
mA 0 , (FNsinq ) (hctgq) Px 0
FN
Px
hcosq
2） BD杆旳最大应力： s max FN max PL A hAcosq
突变规律： 1、从左边开始，向左旳力产生正旳轴力，轴力图向上突变。 2、从右边开始，向右旳力产生正旳轴力，轴力图向上突变。 3、突变旳数值等于集中力旳大小。
即：离端面不远处，应力分布就成为均匀旳。
§2–3 直杆轴向拉压时斜截面上旳应力
一、斜截面上旳内力
n
材料力学第二章 轴向拉伸和压缩

材料力学第二章 轴向拉伸和压缩

伸长 l2 0.24mm 缩短
2、计算各杆轴向变形
C
l 2 =1m a =170mm
B'
B2
F
l1 0.48mm
3、由变形的几何条件确定B点的位移 分别以A为圆心，AB1为半径，C为圆 心，CB1为半径画弧，相较于B’点，
B"
小变形条件，可以用切线代替弧线。
材料力学
第2章 轴向拉伸和压缩
FN FN ( x)
轴力方程
即为轴力图。
即：FN随x的变化规律
以x为横坐标，以FN为纵坐标，绘制FN F（ ）的关系图线， N x
FN
正的轴力画在x轴的上侧，负的画在下侧.
x
材料力学
第2章 轴向拉伸和压缩
例题1
等值杆受力如图所示，试作其轴力图
F =25kN F ４=55kN ４ １=40kN F
纵向线 即： 原长相同
变形相同
横截面上各点的纵向线应变相等
c
拉压杆变形几何方程.
反映了截面上各点变形之间的几何关系.
材料力学
第2章 轴向拉伸和压缩
§2-2 横截面上的正应力 应力分布规律 找变形规律 研究思路： 试验观察 综合几何方面、物理方面、静力学方面推导应力计算公式
一、几何方面
F
a' b'
材料力学
第2章 轴向拉伸和压缩
第二章 轴向拉伸和压缩
材料力学
第2章 轴向拉伸和压缩
• • • • • •
本章主要内容 轴力及轴力图 横截面上的应力 拉压杆的变形、胡克定律 强度计算 材料的力学性质
材料力学
第2章 轴向拉伸和压缩
§2-1 概述 一、工程实际中的轴向拉压杆
材料力学 第二章拉伸、压缩与剪切

材料力学 第二章拉伸、压缩与剪切

FN1 2.62KN FN 2 1.32KN
根据轴力图可以显示各段轴力的大小以及各段的变形是拉伸或压缩
9
§2-2 轴向拉伸或压缩时横截面上的内力与应力
2.应力
轴力的大小并不能用来判断杆件是否有足够的强度，如：
F
F
F
F
细杆先被拉断，说明拉杆的强度不仅与轴力的大小有关，还 与拉杆的的横截面有关，所以必须用横截面上的应力来度量 杆件的受力程度。
3
§2-1 轴向拉伸与压缩的概念与实例
1.轴向拉伸与压缩的实例
2.拉伸压缩动画示范
5
§2-1 轴向拉伸与压缩的概念与实例
3.拉伸与压缩的受力特点
作用于杆件上的外力合力的作用线与杆件的轴 线重合，杆件变形是沿轴线方向伸长或缩短的。
6
§2-2 轴向拉伸或压缩时横截面上的内力与应 力
F1 FN1 0 FN1 F1 2.62 KN (压力)
F1 F2 FN2 0 FN2 F1 F2 1.32KN(压力)
FN 2 F3 0 FN 2 F3 1.32 KN (压力)
8
§2-2 轴向拉伸或压缩时横截面上的内力与应力
轴力图:用平行于杆件轴线的坐标表示横截面的位置， 用垂直于杆件轴线的坐标表示横截面上轴力的数值，从 而绘出表示轴力沿杆轴变化规律的图线。
铸铁压缩时，仍在较小在变形下
突然破裂，破坏断面的法线与轴
线大致成45°角。表明沿斜截面
相对错动而破坏。抗压强度约比
抗拉强度高4－5倍。
24
§2-7 失效、安全因数和强度计算
一、失效 构件因强度、刚度、稳定性等原因不能正常工作。 强度条件引起的失效： 脆性材料制成的构件在拉应力下，当变形很小时就突然断裂； 塑性材料制成的构件在拉断之前已经出现塑性变形，由于不 能保持原有的形状和尺寸，它已经不能正常工作。断裂与出现 塑性变形统称为失效。
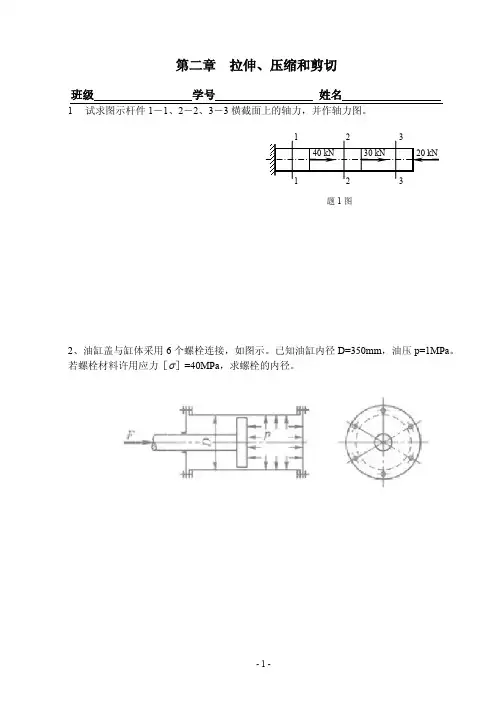
【可编辑全文】材料力学-第二章-拉压与剪切

【可编辑全文】材料力学-第二章-拉压与剪切

班级 学号 姓名1 试求图示杆件1－1、2－2、3－3横截面上的轴力，并作轴力图。

2、油缸盖与缸体采用6个螺栓连接，如图示。

已知油缸内径D=350mm ，油压p=1MPa 。

若螺栓材料许用应力［ ］=40MPa ，求螺栓的内径。

题1图140 kN 30 kN20 kN122 33班级 学号 姓名3 图示木制桁架受水平力P 作用。

已知P=80kN[][]MPa MPa 10,8==压拉σσ，试设计AB 、AD 两杆的横截面积。

4 图示结构，杆1、2的横截面均为圆形，直径分别为d 1=30mm , d 2=20mm 。

两杆材料相同，许用应力[σ]=160MPa ，在节点A 处受铅直力P=80kN 。

试校核结构的强度。

A B C D P60° 60° 30° 30°BC A P 12 30° 45°班级学号 姓名5、某铣床工作台进给油缸如图示，缸内油压p=2MPa ，油缸内径D=75mm ，活塞杆直径 d=18mm 。

已知活塞材料的许用应力［σ］=50MPa ，试校核活塞杆的强度。

6、简易吊车如图所示。

AB 为木杆，横截面积 21cm 100=A ，许用压应力[]MPa 71=σ。

BC 为钢杆，横截面积22cm 6=A ，许用拉应力[]MPa 1602=σ。

试求许可吊重F 。

F30°AB C木杆 钢杆第二章 拉伸、压缩和剪切班级 学号 姓名7、 图示拉杆沿斜截面m －m 由两部分胶合而成。

设在胶合面上许用拉应力[]MPa 100=σ，许用切应力[]MPa 50=τ，并设胶合面的强度控制杆件的拉力。

试问：为使杆件承受最大拉力F ，α角的值应为多少？若杆件横截面面积为4cm 2，并规定α≤60°，试确定许可载荷F 。

8、变截面杆如图所示。

已知：21cm 8=A ，22cm 4=A ， GPa 200=E 。

试求杆的总伸长l ∆。

材料力学课件(路桥)第2章拉伸、压缩


A
N3
N2 N2
F
A
2021/7/13
F
4
D 2
C
B 几何方程——变形协调方程：
3
L1L3cos
1
物理方程——弹性定律：
A
L1
L2
L3
L1
N 1 L1 E 1 A1
L3
N 3 L3 E 3 A3
补充方程：由几何方程和物理方程得。
N1L1 N3L3 cos
A’
E1A1 E3A3
解由平衡方程和补充方程组成的方程组，得:
物理方程及补充方程：
2021/7/13
L1N E11A L11 N E22A L22
L2
7
P
P
解平衡方程和补充方程，得:
y
4N1
N 1 0 .0 7 P ; N 2 0 .7 2 P
N2
求结构的许可载荷：
角钢面积由型钢表查得: A1=3.086cm2
N 10.07PA 11
P A 1 1 / 0 . 0 7 3 0 8 . 6 1 6 0 / 0 . 0 7 7 0 5 . 4 k N
16
知识点的回顾
￥ 超静定问题 ￥ 静力平衡方程，变形协调方程（几何方程），
物理方程 ￥ 温度应力，装配应力 ￥ 应力集中
2021/7/13
17
2021/7/13
18
问题？
注：文档资料素材和资料部分来
2021/7/13
6
例2 木制短柱的四角用四个4.0440的等边角钢加固，角钢和木
材的许用应力分别为[]1=160MPa和[]2=12MPa，弹性模量分别
为E1=200GPa 和 E2 =10GPa；求许可载荷P。

材料力学第二章+拉压


FN4
20kN
第二章 轴向拉伸和压缩
§2.2 内力计算
40kN A B 300 50
55kN 25kN C 500 D 400
20kN E
FN
(kN) 10
FN1=10kN （拉力） FN2=50kN （拉力） FN3= - 5kN （压力） FN4=20kN （拉力）
+
20
+
5
FNmax 50( kN ) 发生在BC段内任一横截面上
寸。）
第二章 轴向拉伸和压缩 圣维南原理：
§2.3 拉压杆的应力
在静力等效条件下，不同的加载方式只对加载处附近区 域的应力分布有影响，离开加载处较远的部分，其应力分布 并没有显著的差别。
第二章 轴向拉伸和压缩
§2.3 拉压杆的应力
例题2-3 试求此正方 形砖柱由于荷载引起的横 截面上的最大工作应力。 已知F = 50 kN。
FN
O
x
第二章 轴向拉伸和压缩
§2.2 内力计算
例题1
一等直杆其受力情况如图所示， 作杆的轴力图.
40kN A 600 B 300
55kN 25kN C 500 D 400
20kN E
第二章 轴向拉伸和压缩
40kN
§2.2 内力计算
55kN 25kN
300
20kN D 400
E
A
600
B
C
500
§2.2 内力计算
1、截面法
截开 在求内力的截面m-m 处， 假想地将杆截为两部分. 代替 取左部分为研究对象。弃去 右部分。弃去部分对研究对 象的作用，以截开面上的内 m F m FN m
F
m

第二章 拉伸与压缩材料力学


σ
b a
d
σ = E = tgα ε
c
e
比例极限 σ p
弹性极限 σ e
α
O
ε
2. 屈服阶段 bc
σ
b a
上屈服极限
下屈服极限
d
c e
屈服极限
σs
O
ε
表面磨光的试件， 表面磨光的试件，屈服时可在试件表面看见 与轴线大致成45°倾角的条纹。 与轴线大致成 °倾角的条纹。这是由于材 料内部晶格之间相对滑移而形成的， 料内部晶格之间相对滑移而形成的，称为滑 移线。因为在45°的斜截面上剪应力最大。 移线。因为在 °的斜截面上剪应力最大。
3
满足强度条件。 满足强度条件。
例2：图示三角形托架,其杆 是由两根等 ：图示三角形托架 其杆AB是由两根等 其杆 边角钢组成。已知P=75kN, 边角钢组成。已知 [σ]=160MPa, 试选择等边角钢的型号。 试选择等边角钢的型号
解：由ΣM C = 0, 得: N AB = P = 75 kN
F E
0
30
D
c
A
B
P
3000 750 600 3200
解：1、分析杠件内力，确定危 险构件： 取AB杆研究： 由 ∑ M
=0 A
3
N
E
EF
N
BC
× 3.75 − P × 3 = 0 39 × 10 × 3
1、实验现象的观测 P 在试件上画上网格后加载可 F 观测到：(1)网格的直角不变， (2)两横线之间均匀伸长， (3)纵向线之间均匀收缩。 由此可推断： (1) (2)
P`
γ = 0, τ = 0 →
σ ≠ 0, σ
沿横截面均匀分布

材料力学第2章+轴向拉伸与压缩


第二章 轴向拉伸和压缩
§2-3应力·拉（压）杆内的应力
1. 应力的概念
若考察受力杆截面上M点处
应力：指受力杆件某一横 截面上一点处的内力集度 （内力分布的密集程度）
应力,可在M点周围取一很
小面积ΔA,设 ΔA面积上分 布内力的合力为ΔF,则 ΔA
上内力平均集度为:
F M A
26
Pm = F/A
Pm即A上的平均应力
第二章 轴向拉伸和压缩
若将力F由自内端A至杆B点处(图d)，则其AB段内任一横 截面上的轴力都将等于零(图e)．而BC段内任一横截面n-n上的 轴力仍等于F(图f)，保持不变。
FN = 0
14
§2-2内力·截面法·轴力及轴力图 2．截面法、轴力
第二章 轴向拉伸和压缩
原因：这是因为集中力F由自由端A移至B点 后，改变了杆件AB段的变形。而并不改变BC 段的变形
第二步、绘制轴力图
第二章 轴向拉伸和压缩
FN kN
10
FN图kN
25
_
x
10
20
第二章 轴向拉伸和压缩
§2-2内力·截面法·轴力及轴力图
例2.2
30kN
A
30kN
作图示杆件的轴力图，并指出| FN |max
1
2
90kN
60kN
1
B
2
解：1、计算杆件各段的轴力。
C
AB 段
1
2
x FN1
FN2
1
2
60kN
第二章 轴向拉伸和压缩
§2-2内力·截面法·轴力及轴力图 2．截面法、轴力
注意：静力学中的力（或力偶)的可移性原理，在用截面法 求内力的过程中是有限制的。如图a所示拉杆在自由端A承 受集中力F，由截面法可得，杆任一横截面m—m或n—n” 上的轴力FN、均等于F(图b，c）。

材料力学拉伸、压缩与剪切

当α＝900 时
σ/2
τ max
τ min
σ/2
450
-450
2.4 材料在拉伸时的力学状态
力学性能：材料在外力作用下表现出的变形和破坏特性。 不同的材料具有不同的力学性能
01
材料的力学性
*
2.4 材料在拉伸时的力学状态
拉伸标准试样 压缩试件——很短的圆柱型： h = (1.5—3.0)d h d
s
b
e
p
f
O
f
′
h
a
b
c
e
*
2.4 材料在拉伸时的力学状态
卸载定律及冷作硬化
e p－塑性应变
e e －弹性应变
预加塑性变形, 可使s e 或s p 提高
卸载定律： 当拉伸超过屈服阶段后，如果逐渐卸载，在卸载过程中，应力——应变将按直线规律变化。
冷作硬化：在常温下将钢材拉伸超过屈服阶段，卸载后短期内又继续加载，材料的比例极限提高而塑性变形降低的现象。
2. 轴力图与最大轴力
轴力图为直线
2.2 轴向拉伸或压缩时横截面上的内力和应力
1.变形现象(Deformation phenomenon)
（1） 横向线ab和cd仍为直线,且仍然垂直于轴线;
（2） ab和cd分别平行移至a'b'和c'd' , 且伸长量相等.
结论：各纤维的伸长相同,所以它们所受的力也相同.
FN1
A
B
C
D
FA
FB
FC
FD
A
B
C
D
FA
FB
FC
FD
O
2.2 轴向拉伸或压缩时横截面上的内力和应力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

确定的方法是:
在ε轴上取0.2％的点,
ε
对此点作平行于σ－ε曲线
的直线段的直线（斜率亦为
E）,与σ－ε曲线相交点对
应的应力即为σ0.2 .
Ⅳ 材料的力学性质/六 几种非金属材料的力学性能
混凝土
Ⅳ 材料的力学性质/六 几种非金属材料的力学性能
木材
Ⅳ 材料的力学性质/六 几种非金属材料的力学性能
玻璃钢
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
低碳钢拉伸时的应力-应变图
弹性阶段
B
比例极限 p
弹性极限 e
A
弹性模量 E
力与变形成正比的规律
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
低炭钢拉伸时的应力-应变图 屈服阶段
屈服极限 s
屈服现象： 应力－应变曲线上的锯齿线 试件表面的滑移线
关于 0.2 有如下四种论述，请判断哪一个是正确的： （A）弹性应变为0.2%时的应力值； （B）总应变为0.2%时的应力值； （C）塑性应变为0.2%时的应力值； （D）塑性应变为0.2时的应力值。 正确答案是（ C ）
Ⅳ 材料的力学性质/课堂讨论题
低碳钢加载→卸载→ 再加载路径有以下四种，请判断哪一 个是正确的：（ ） （A）OAB →BC →COAB ； （B）OAB →BD →DOAB ； （C）OAB →BAO→ODB； （D）OAB →BD →DB。 正确答案是（ D ）
Ⅳ 材料的力学性质/课堂讨论题
塑性材料冷作硬化后，材料的力学性能发生了变化。试判断以 下结论哪一个是正确的： （A）屈服应力提高，弹性模量降低； （B）屈服应力提高，塑性降低； （C）屈服应力不变，弹性模量不变； （D）屈服应力不变，塑性不变。 正确答案是（ B ）
低碳钢材料在拉伸实验过程中，不发生明显的塑性变形时，承受的最 大应力应当小于的数值，有以下4种答案，请判断哪一个是正确的： （A）比例极限； （B）屈服极限； （C）强度极限； （D）许用应力。 正确答案是（ B ）
试件：短柱
l=(1.0~3.0)d
(2)屈服阶段，拉伸和压缩
时的屈服极限相同,即
s
s
(3)屈服阶段后，试样越压
越扁，无颈缩现象，测不
出强度极限 b 。
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
Ⅳ 材料的力学性质/三 脆性材料在拉压时的力学性能
1 铸铁拉伸时的应力-应变曲线
拉伸
b
脆 性
材料力学
第二章 拉伸与压缩
同济大学航空航天与力学学院 顾志荣
第二章 拉伸与压缩
Ⅳ 材料的力学性质 一 概述 二 塑性材料在拉压时的力学性能 三 脆性材料在拉压时的力学性能 四 塑性、脆性材料的强度指标(失效应力) 五 其它材料在拉压时的力学性能 六 几种非金属材料的力学性能
Ⅳ 材料的力学性质/一 概述
Ⅳ 材料的力学性质/课堂讨论题
关于低碳钢试样拉伸至屈服时，有以下结论，请判断哪一个是正确 的： （A）应力和塑性变形很快增加，因而认为材料失效； （B）应力和塑性变形虽然很快增加，但不意味着材料失效； （C）应力不增加，塑性变形很快增加，因而认为材料失效； （D）应力不增加，塑性变形很快增加，但不意味着材料失效。 正确答案是（ C ）
材料暂时失去抵抗变 形的能力。
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
低碳钢拉伸时的应力-应变图
Ab Bs
强化阶段
E
E
1
1
强度极限 b
o p e A'
p e
材料又恢复并增强了抵抗变形的能力。
卸载规律 冷作（应变）强化现象：材料比例极限提 高，塑性降低．
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
b
Ⅳ 材料的力学性质/四 塑性、脆性材料的强度指标(失效应力)
强度指标(失效应力)
韧性金属材料
脆
性
材
料
塑性材料
s
脆性材料
b
Ⅳ 材料的力学性质/五 其它材料在拉压时的力学性能
锰钢
强铝
退火球墨铸铁
o
Ⅳ 材料的力学性质/五 其它材料在拉压时的力学性能
名义屈服极限σ0.2的确定
σ
b
0.2
o
0.2%
低碳钢拉伸时的力学性能小结
一条应力-应变曲线
二个规律（F与△l成正比规律，卸载规律）
三个现象(屈服、冷作强化、颈缩) 四个阶段(弹性、屈服、强化、颈缩) 五个性能指标( E 、 s 、 b 、 、 )
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
二、低碳钢压缩时的力学性能 (1)弹性阶段与拉伸时相同， 杨氏模量、比例极限相同；
拉伸：与无明显的线性关系，
材 料
拉断前应变很小.只能总应变为0.1%时的割线斜率来
度量。破坏时沿横截面拉断。
Ⅳ 材料的力学性质/三 脆性材料在拉压时的力学性能
1 铸铁压缩时的力学性能
b
脆
性
材
料
压缩：b (4.0~5.0)b ，
适于做抗压构件。破坏时破裂面
与轴线成45°~ 55°。
1 为什么要研究材料的力学性质
为构件设计提供合理选用材料的依据。
强度条件： 工作应力FAN []
理论计算求解
通过试验研究材料力学性质得到
2 何谓材料的力学性能
材料在受力、变形过程中所表现的行为及特征指标。
Ⅳ 材料的力学性质/一 概述
3 材料的力学性质与哪些因素有关 与材料的组成成分、结构组织（晶体或非晶体）、应
关于材料的力学一般性能，有如下结论，请判断哪一个是正确的： （A）脆性材料的抗拉能力低于其抗压能力； （B）脆性材料的抗拉能力高于其抗压能力； （C）塑性材料的抗拉能力高于其抗压能力； （D）脆性材料的抗拉能力等于其抗压能力。 正确答案是（ A ）
力状态、温度和加载方式等诸因素有关。
4 塑性材料与脆性材料 断裂前产生较大塑性变形的材料(如低碳钢)称为塑性
材料。 断裂前塑性变形很小的材料(如铸铁、石材)称为脆性
材料。
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
1低碳钢在拉伸时的力学性能 低碳钢——含碳量在0.25%以下的碳素钢。 低碳钢拉伸时的应力－应变图
低碳钢拉伸时的应力-应变图 颈缩阶段
断裂
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
试件断裂过程图
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能
塑性性能指标
（1）延伸率
l1l 100%
l
5%的材料为塑性材料； 5%的材料为脆性材料。
（2）截面收缩率 AA110% 0
A
Ⅳ 材料的力学性质/二 塑性材料在拉压时的力学性能