下载文档原格式
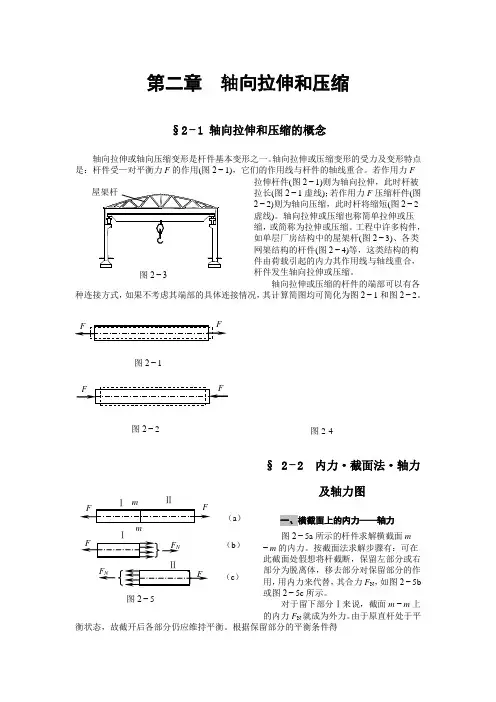
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸，此时杆被2−1虚线)；若作用力F 压缩杆件(图(图2−2工程中许多构件，(图2−3)、各类(图2−4)等，这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有：可在此截面处假想将杆截断，保留左部分或右部分为脱离体，移去部分对保留部分的作用，用内力来代替，其合力F N ，如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说，截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态，故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N（a ）（b ） （c ）图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中，F N 为杆件任一截面m −m 上的内力，其作用线也与杆的轴线重合，即垂直于横截面并通过其形心，故称这种内力为轴力，用符号F N 表示。
若取部分Ⅱ为脱离体，则由作用与反作用原理可知，部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。
同样也可以从脱离体的平衡条件来确定。
二、轴力图当杆受多个轴向外力作用时，如图2−7a ，求轴力时须分段进行，因为AB 段的轴力与BC 段的轴力不相同。
要求AB 段杆内某截面m −m 的轴力，则假想用一平面沿m −m 处将杆截开，设取左段为脱离体(图2−7b)，以F N Ⅰ代表该截面上的轴力。
于是，根据平衡条件∑F x ＝0，有 F F -=ⅠN负号表示的方向与所设的方向相反，即为压力。
要求B C 段杆内某截面n-n 的轴力，则在n −n 处将杆截开，仍取左段为脱离体（图2−7c ），以F N Ⅱ代表该截面上的轴力。
于是，根据平衡条件∑F x ＝0，有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时，由于各段杆轴力的大小及正负号各异，所以为了形象地表明各截面轴力的变化情况，通常将其绘成“轴力图”(图2−7d)。
大学时材料力学复习提纲
第二章轴向拉伸与压缩
1、轴向拉伸的受力特点；
2、截面法求变截面上的轴力及绘制轴力图；
3、横截面上的正应力计算
4、轴向拉压杆件形变量；
5、泊松比
6、低碳钢、铸铁试验性质，应力应变图等
7、简单超静定
第三章扭转
1、
2、
3、
4、扭转受力特点，横截面上扭转产生的剪应力分布；计算扭矩和画扭矩图；横截面上剪应力计算和强度校核，抗扭截面系数等；低碳钢和铸铁扭转试验特点；第四章弯曲内力
1、会列剪力方程和弯矩方程并画剪力图和弯矩图；
2、载荷集度、剪力和弯矩间的微分关系；
第五章弯曲应力
1、弯曲受力特点，中性层、中性轴的意义；
2、铸铁材料横截面上正应力的计算；
第七章应力分析
1、应力状态的概念；
2、斜截面上的应力状态；
3、平面应力状态下主应力、主平面计算
4、应力圆；
5、纯剪切的意义；
6、四个强度理论及四个相当应力；
第八章组合变形
1、弯扭组合的第三和第四强度理论（单向弯曲和扭转）
第九章压杆稳定
1、压杆临界压力公式，四种约束类型；
2、临界应力总图的意义；
3、压杆稳定性校核；
第十三章能量法
1、卡式定理、互等定理和单位载荷法解决梁和钢架变形问题。
附录平面图形的几何性质
1、极惯性矩、惯性矩的概念注：以上内容是三套卷子必考内容。
题型
一基本知识题（包含10个空，3个选择题）
二、三、四、五、六、七、共六个计算题（轴向拉压、弯曲、应力分析、组合变形、压杆稳定、能量法）。
