2018年高三最新 杭州市2018学年第一学期期末统测数学试卷(理科) 精品

2018学年第一学期杭州市高三年级教学质量检测数学试题参考答案及评分标准一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．11．3；312．－12 13．(0，1)；y 14．288－24π，264＋12π15．4 16．[2，4]17．k ＞12三、解答题：本大题共5小题，共 74分．解答应写出文字说明、证明过程或演算步骤． 18．（本题满分14分）解 （Ⅰ）f (5π6)＝sin 5π3＋3cos 5π3＝－3＋3＝0． ……4分（Ⅱ）因为 f (x )＝2sin π23x ⎛⎫+ ⎪⎝⎭，当x ∈[0，π4]时，ππ5π2,336x ⎡⎤+∈⎢⎥⎣⎦，所以sin π23x ⎛⎫+ ⎪⎝⎭∈1,12⎡⎤⎢⎥⎣⎦， 所以f (x )的取值范围为[1，2]．……10分19．（本小题满分15分） 解 （Ⅰ）当k ＝1时，|1|2x x --－k (x －1)2＝0， 所以 | x －1 |∙11|(2)2x x x |----＝0，所以 | x －1 |＝0或1－| x －1 |(x －2)＝0，所以解x ＝1，x ．……7分（Ⅱ）因为| x －1 |∙(12x -－k | x －1 | )＝0，即| x －1 |＝0或12x -－k | x －1 |＝0，当| x －1 |＝0时，x ＝1，此时k ∈R ；所以12x -－k | x －1 |＝0有三个不等于1的解， 即1k＝| x －1 |∙(x －2)有三个不等于1的解， 根据函数y ＝| x －1 |∙(x －2)的图象，所以－14＜1k＜0，即k ＜－4． ……8分20．（本题满分15分）解（Ⅰ）由AD ⊥BC 可知，| DM |＝| AM |，| DN |＝| AN |，所以∠MDN ＝∠MAN ，因为 DM ∙DN ＝12cos ∠MAN ＝－6， 所以cos ∠MAN＝－12， 所以 | BC |2＝| AB |2＋| AC |2－2| AB |∙| AC | cos ∠MAN ＝148，所以 | BC |＝237．……8分（Ⅱ）因为||||DM DB DN DC DB DC ⋅⋅+＝12( | DB |＋| DC | )＝5， 所以 | BC |＝10，所以∠BAC =90°．……7分21．（本题满分15分） 解：（Ⅰ）设等差数列{a n }的公差为d ，则⎩⎪⎨⎪⎧6a 1＋15d ＝60，a 1(a 1＋20d )＝(a 1＋5d )2，解得125d a =⎧⎨=⎩， ∴ a n ＝2n ＋3． S n ＝(82)2n n +＝n (n ＋4)． ……7分（Ⅱ）由b n ＋1－b n ＝a n ， ∴b n －b n －1＝a n －1(n ≥2，n ∈N *)． 当n ≥2时，b n ＝(b n －b n －1)＋(b n －1－b n －2)＋…＋(b 2－b 1)＋b 1 ＝a n －1＋a n －2＋…＋a 1＋b 1 ＝(n －1)(n －1＋4)＋3＝n (n ＋2)． 对b 1＝3也适合， ∴ b n ＝n (n ＋2)(n ∈N *)．1 xyO∴1nb ＝1(2)n n +＝12∙(1n －1+2n )． T n ＝12∙(1－13＋12－14＋…＋1n －1+2n ) ＝12(32－1n ＋1－1n ＋2)＝3n 2＋5n 4(n ＋1)(n ＋2)．……8分22．（本题满分15分）解：（Ⅰ）（i ）根据题意，f ′(x )＝221x ax x++， 所以方程 2x 2＋ax ＋1＝0有两个正根t 1，t 2（不妨设t 1＜t 2），所以 004a ∆>⎧⎪⎨->⎪⎩，解得a ＜－． ……3分（ii ）易知f (x )在x ＝t 1时取到极大值，在x ＝t 2时取到极小值．由（i ）知 2t 12＋at 1＋1＝0， 所以 f (t 1)＝－t 12＋ln t 1－1． 令 g (x )＝－x 2＋ln x －1，所以g ′(x )＝1x－2x ， 由1x－2x ＝0，解得x ＝2．所以 g (x )≤g (2)＝ln 2－32＜0， 所以f (t 1)＜0，故f (x )至多只有一个零点．又f (－a )＝ln (－a )＞0，可知f (x )存在唯一零点．……5分（Ⅱ）由题意知：2x 1＋a ＋11x ＋2x 2＋a ＋21x ＝0，即 a ＝－(x 1＋x 2)－1212+2x x x x ， 所以f (x 1)－f (x 2)＝x 12－x 22＋a (x 1－x 2)＋ln 12x x＝－12(12x x －21x x )＋ln 12x x ， 设t ＝12x x ∈(1，2)，记h (t )＝－2t＋12t ＋ln t ，则 h ′(t )＝－12－212t ＋1t＝－12(1t ＋1)2≤0，故h (t )单调递增，所以h (t )∈(h (2)，h (1))， 即h (t )∈(－34＋ln2，0)．……7分。

浙江省杭州市2018届高三上学期期末教学质量检测数学试题(WORD版)杭州市2017-2018学年第一学期高三年级数学试题一、选择题1.设集合 $A=\{x|x+2\leq2\}$，$B=[0,4]$，则 $C=(A\capB)$。

选项：A。

$R$B。

$\emptyset$C。

$\{x|x\in R,x\neq-2\}$D。

$\{x|x\in[0,2]\}$2.双曲线 $x^2/4-y^2/9=1$ 的渐近线方程为（）。

选项：A。

$y=\pm x$B。

$y=\pm x/3$XXXD。

$y=\pm3x/2$3.设数列 $\{a_n\}$ 的通项公式为 $a_n=kn+2(n\in N)$，则“$k>2$”是“数列 $\{a_n\}$ 为递增数列的”（）。

选项：A。

充分不必要条件B。

必要不充分条件C。

充要条件D。

既不充分又不必要条件4.若函数 $f(x)$ 的导函数 $f'(x)$ 的图象如图所示，则（）。

选项：A。

函数 $f(x)$ 有1个极大值，2个极小值B。

函数 $f(x)$ 有2个极大值，2个极小值C。

函数 $f(x)$ 有3个极大值，1个极小值D。

函数 $f(x)$ 有4个极大值，1个极小值5.若直线 $y=x$ 与曲线 $y=e^x$ 相切，则 $m=$（）。

选项：A。

1B。

2C。

$-1$D。

$-2$6.设不等式组 $\begin{cases}x+y\leq1\\y\geqmx\end{cases}$ 所表示的区域面积为 $S(m\in R)$，若 $S\leq1$，则（）。

选项：A。

$m\leq-2$B。

$-2\leq m\leq$C。

$<-m\leq2$D。

$m\geq2$7.在函数 $f(x)=\frac{x}{a-1}$ 中，$a>1$ 且 $a\neq1$，则函数 $f(x)$ 的奇偶性为（）。

选项：A。

与 $a$ 无关，且与 $b$ 无关B。

与 $a$ 有关，且与 $b$ 有关C。

杭州市2018届高三数学第一次教学质量检测（理含答案）
5
c
数学（理科）
第Ⅰ卷（共60分）
一、选择题本大题共8个小题,每小题5分,共40分在每小题给出的四个选项中，只有一项
是符合题目要求的
1设集合，，则（）
A． B． c． D．
2若，则（）
A． B． c．2 D．-2
3某几何体的三视图如图所示（单位），则该几何体的侧面的面积是（）
A． B．2 c． D．
4命题“ 或”的否定是（）
A．且 B．或
c．且 D．或
5设，满足若函数存在零点，则（）
A． B． c． D．
6设点为有共焦点的椭圆和双曲线的一个交点，且，椭圆的离心率为，双曲线的离心率为若，则（）
A． B． c． D．
7在中，是直角，，，的内切圆交，于点，，点是图中阴影区域内的一点（不包含边界）若，则的值可以是（）A．1 B．2 c．4 D．8
8记是各项均为正数的等差数列的前项和，若，则（）。

2017—2018学年度第一学期期末联考试题高三数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分全卷满分150分，考试时间120分钟．注意：1. 考生在答题前，请务必将自己的姓名、准考证号等信息填在答题卡上．2. 选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试卷上无效．3. 填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内．答在试题卷上无效．第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．把答案填在答题卡上对应题号后的框内，答在试卷上无效．1．设集合{123}A =，，，{45}B =，，{|}M x x a b a A b B ==+∈∈，，，则M 中的元素个数为A ．3B ．4C ．5D ．62．在北京召开的第24届国际数学家大会的会议，会议是根据中国古代数学家赵爽的弦图（如图）设计的，其由四个全等的直角三角形和一个正方形组成，若直角三角形的直角边的边长分别是3和4，在绘图内随机取一点，则此点取自直角三角形部分的概率为 A ．125B ．925C ．1625D ．24253．设i 为虚数单位，则下列命题成立的是A ．a ∀∈R ，复数3i a --是纯虚数B ．在复平面内i(2i)-对应的点位于第三限象C ．若复数12i z =--，则存在复数1z ，使得1z z ∈RD ．x ∈R ，方程2i 0x x +=无解4．等比数列{}n a 的前n 项和为n S ，已知3215109S a a a =+=，，则1a =A ．19B ．19-C ．13D ．13-5．已知曲线421y x ax =++在点(1(1))f --，处切线的斜率为8，则(1)f -=试卷类型：A天门 仙桃 潜江A ．7B ．－4C ．－7D ．4 6．84(1)(1)x y ++的展开式中22x y 的系数是A ．56B ．84C ．112D ．1687．已知一个空间几何体的三视图如图，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 A ．4cm 3B ．5 cm 3C ．6 cm 3D ．7 cm 38．函数()sin()(0,0)f x A x A ωϕω=+>>的图像如图所示，则(1)(2)(3)(18)f f f f ++++的值等于ABC 2D ．19．某算法的程序框图如图所示，其中输入的变量x 在1，2，3…，24 这24个整数中等可能随机产生。

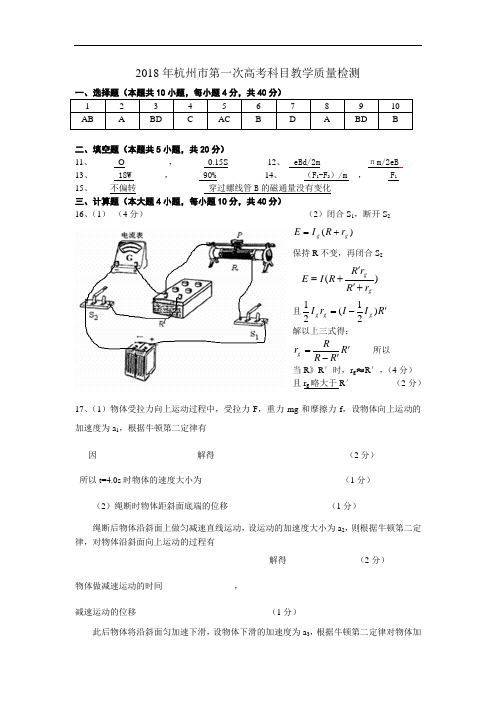
2018年杭州市第一次高考科目教学质量检测二、填空题（本题共5小题，共20分）11、______O__________，_______0.15S_______ 12、_ eBd/2m _______πm/2eB 13、______18W _______，_______90%________ 14、_____（F 1-F 2）/m _ ，_____ F 1 _____ 15、____不偏转____ ____________穿过螺线管B 的磁通量没有变化 三、计算题（本大题4小题，每小题10分，共40分） 16、（1） （4分） （2）闭合S 1，断开S 2)(g g r R I E +=保持R 不变，再闭合S 2且'-=R I I r I g g g )21(21 解以上三式得：''-=R R R Rr g 所以当R 》R ′时，r g ≈R ′，（4分） 且r g 略大于R ′ （2分）17、（1）物体受拉力向上运动过程中，受拉力F ，重力mg 和摩擦力f ，设物体向上运动的加速度为a 1，根据牛顿第二定律有因解得（2分）所以t=4.0s 时物体的速度大小为 （1分）（2）绳断时物体距斜面底端的位移（1分）绳断后物体沿斜面上做匀减速直线运动，设运动的加速度大小为a 2，则根据牛顿第二定律，对物体沿斜面向上运动的过程有解得（2分）物体做减速运动的时间，减速运动的位移（1分）此后物体将沿斜面匀加速下滑，设物体下滑的加速度为a 3，根据牛顿第二定律对物体加)(gg r R r R R I E +''+=速下滑的过程有 解得（2分）设物体由最高点到斜面底端的时间为t 3，所以物体向下匀加速运动的位移（1分）18、（1）时刻t ，棒的速度 v=at此时棒中感应电动势为 E=BLv=Blat 此时棒中的感应电流为 I =RE2（1分）由牛顿第二定律得 F-BIL=ma （2分）得 F =ma t RaL B +222 （1分） （2）细线拉断时满足 BIL=T （1分）即 0222t RaL B T =（2分） （3） 拉力F 撤去，系统合外力为零，动量守恒 m v 0=2mv （2分）v 0=at 0 v=21at 0 （1分） 19、（1）不守恒。

浙江省杭州市2018届高三上学期期末教学质量检测数学试题卷一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}[]22,0,4A x x B =+≤=，则()R C A B =I （ ）A. RB.{}0C.{},0x x R x ∈≠ D.∅ 2.双曲线2214y x -=的渐近线方程为（ ） A.12y x =± B.2y x =± C.3y x =± D.5y x =± 3.设数列{}n a 的通项公式为*2()n a kn n N =+∈，则“2k >”是“数列{}n a 为递增数列的”（ ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.若函数()f x 的导函数'()f x 的图象如图所示，则（ ）A. 函数()f x 有1个极大值，2个极小值B. 函数()f x 有2个极大值，2个极小值C. 函数()f x 有3个极大值，1个极小值D. 函数()f x 有4个极大值，1个极小值5.若直线y x =与曲线x m y e +=（m R ∈，e 为自然对数的底数）相切，则m =（ ）A. 1B. 2C. 1-D. 2-6.设不等式组01y x y y mx ≥⎧⎪+≤⎨⎪≥⎩，所表示的区域面积为()S m R ∈，若1S ≤，则（ ） A. 2m ≤- B. 20m -≤≤ C. 02m <≤ D. 2m ≥7.设函数2()1x f x b a =+-（0a >且1a ≠），则函数()f x 的奇偶性（ ） A. 与a 无关，且与b 无关 B. 与a 有关，且与b 有关C. 与a 有关，但与b 无关D. 与a 无关，但与b 有关8.在三棱锥P ABC -中，PA ⊥平面ABC ，90BAC ∠=o，,D E 分别是,BC AB 的中点，AB AC ≠，且AC AD >.设PC 与DE 所成角为α，PD 与平面ABC 所成角为β，二面角P BC A --为γ，则（ ）A.αβγ<<B.αγβ<<C.βαγ<<D.γβα<<9.设函数2()(,)f x ax bx c a b R =++∈，记M 为函数()y f x =在[1,1]-上的最大值，N 为a b +的最大值，则（ ）A. 若13M =，则3N =B. 若12M =，则3N = C. 若2M =，则3N = D. 若3M =，则3N = 10.在四边形ABCD 中，点,E F 分别是,AD BC 的中点，设AD BC m ⋅=u u u r u u u r ，AC BD n ⋅=u u u r u u u r，若 2,1,3AB EF CD ===，则（ ）A. 21m n -=B. 221m n -=C. 21m n -=D. 221n m -=二、填空题：本大题共7小题，多空题每小题6分，单空题每小题4分，共36分.11.设复数52z i=-（其中i 为虚数单位），则复数z 的实部为 ，虚部为 . 12.在一次随机实验中，事件A 发生的概率为p ，事件A 发生的次数为ξ，则期望E ξ= ，方差D ξ的最大值为 .13.在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，5,3,sin 2sin a b C A ===，则sin A = ，设D 为AB 边上一点，且2BD DA =u u u r u u u r ，则BCD ∆的面积为 . 14.如图是某三棱锥的三视图，则该三棱锥的体积为 ，表面积为 .15.在二项式25()()a x a R x +∈的展开式中，若含7x 的项的系数为10-，则a = .16.有红、黄、蓝三种颜色的小球（除颜色外均相同）各4只，都分别标有字母,,,A B C D ，任意取出4只，字母各不相同且三种颜色齐备的取法共有 种.（用数字作答） 17.已知单位向量12,e e u r u u r 的夹角为3π，设122a e e λ=+r u r u u r ，则当0λ<时，a λ+r 的取值范围是 .三、解答题：本大题共5小题，共74分，解答应写出文字说明、证明过程或演算步骤.18.（本小题满分14分）设向量(23sin ,cos ),(cos ,2cos )a x x b x x =-=r r ，() 1.f x a b =⋅+r r（1）求函数()f x 的最小正周期；（2）若方程2()()f x t t t R =-∈无实数解，求t 的取值范围.19.（本小题满分15分）如图，在三棱锥A BCD -中，60BAC BAD DAC ∠=∠=∠=o ，2AC AD ==， 3.AB =（1）证明：AB CD ⊥；（2）求CD 与平面ABD 所成角的正弦值.20.（本小题满分15分）设函数22()().1f x x R x =∈+ （1）求证：2()1f x x x ≥-++；（2）当[1,0]x ∈-时，函数()2f x ax ≥+恒成立，求实数a 的取值范围.21.（本小题满分15分）已知椭圆22:132x y C +=，直线:(0)l y kx m m =+≠，设直线l 与椭圆C 相交于,A B 两点.（1）若3m >，求实数k 的取值范围；（2）若直线,,OA AB OB 的斜率成等比数列（其中O 为坐标原点），求OAB ∆的面积的取值范围.22.（本小题满分15分）设数列{}n a 满足2*113,(1)20().n n n a a a a n N +=-++=∈（1）求证：1n a >；（2）求证：12n n a a +<<；（3）设数列{}n a 的前n 项和为n S ，求证：1222()233().23n n n S n -≤-≤-。

杭州市2017-2018学年第一学期高三年级教学质量检测数学试题卷考生须知：1．全卷分试卷和答题卷，考试结束后，将答题卷上交。

2．试卷共4页，有3大题，22小题。

满分150分，考试时间120分钟。

3．答题前，请务必将自己的姓名，准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。

4．请将答案做在答题卷的相应位置上，写在试卷上无效。

作图时先使用2B 铅笔，确定后必须使用黑色字迹的签字笔或钢笔描黑。

一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}[]22,0,4A x x B =+≤=，则()R C A B =（ ）A. RB.{}0C.{},0x x R x ∈≠ D.∅ 2.双曲线2214y x -=的渐近线方程为（ ） A.12y x =± B.2y x =± C.32y x =± D.52y x =± 3.设数列{}n a 的通项公式为*2()n a kn n N =+∈，则“2k >”是“数列{}n a 为递增数列的”（ ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.若函数()f x 的导函数'()f x 的图象如图所示，则（ ）A. 函数()f x 有1个极大值，2个极小值B. 函数()f x 有2个极大值，2个极小值C. 函数()f x 有3个极大值，1个极小值D. 函数()f x 有4个极大值，1个极小值5.若直线y x =与曲线x m y e +=（m R ∈，e 为自然对数的底数）相切，则m =（ ）A. 1B. 2C. 1-D. 2-6.设不等式组01y x y y mx ≥⎧⎪+≤⎨⎪≥⎩，所表示的区域面积为()S m R ∈，若1S ≤，则（ ） A. 2m ≤- B. 20m -≤≤ C. 02m <≤ D. 2m ≥7.设函数2()1x f x b a =+-（0a >且1a ≠），则函数()f x 的奇偶性（ ） A. 与a 无关，且与b 无关 B. 与a 有关，且与b 有关C. 与a 有关，但与b 无关D. 与a 无关，但与b 有关8.在三棱锥P ABC -中，PA ⊥平面ABC ，90BAC ∠=，,D E 分别是,BC AB 的中点，AB AC ≠，且AC AD >.设PC 与DE 所成角为α，PD 与平面ABC 所成角为β，二面角P BC A --为γ，则（ ）A.αβγ<<B.αγβ<<C.βαγ<<D.γβα<<9.设函数2()(,)f x ax bx c a b R =++∈，记M 为函数()y f x =在[1,1]-上的最大值，N 为a b +的最大值，则（ ）A. 若13M =，则3N = B. 若12M =，则3N = C. 若2M =，则3N = D. 若3M =，则3N = 10.在四边形ABCD 中，点,E F 分别是,AD BC 的中点，设AD BC m ⋅=，AC BD n ⋅=，若 2,1,3AB EF CD ===，则（ ）A. 21m n -=B. 221m n -=C. 21m n -=D. 221n m -=二、填空题：本大题共7小题，多空题每小题6分，单空题每小题4分，共36分.11.设复数52z i=-（其中i 为虚数单位），则复数z 的实部为 ，虚部为 .12.在一次随机实验中，事件A 发生的概率为p ，事件A 发生的次数为ξ，则期望E ξ= ，方差D ξ的最大值为 .13.在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，5,3,sin 2sin a b C A ===，则s i n A = ，设D 为AB 边上一点，且2BD DA =，则BCD ∆的面积为 .14.如图是某三棱锥的三视图，则该三棱锥的体积为 ，表面积为 .15.在二项式25()()a x a R x +∈的展开式中，若含7x 的项的系数为10-，则a = .16.有红、黄、蓝三种颜色的小球（除颜色外均相同）各4只，都分别标有字母,,,A B C D ，任意取出4只，字母各不相同且三种颜色齐备的取法共有 种.（用数字作答）17.已知单位向量12,e e 的夹角为3π，设122a e e λ=+，则当0λ<时，a λ+的取值范围是 .三、解答题：本大题共5小题，共74分，解答应写出文字说明、证明过程或演算步骤.18.（本小题满分14分）设向量(23sin ,cos ),(cos ,2cos )a x x b x x =-=，() 1.f x a b =⋅+（1）求函数()f x 的最小正周期；（2）若方程2()()f x t t t R =-∈无实数解，求t 的取值范围.19.（本小题满分15分）如图，在三棱锥A BCD -中，60BAC BAD DAC ∠=∠=∠=，2AC AD ==， 3.AB =（1）证明：AB CD ⊥；（2）求CD 与平面ABD 所成角的正弦值.20.（本小题满分15分）设函数22()().1f x x R x=∈+ （1）求证：2()1f x x x ≥-++；（2）当[1,0]x ∈-时，函数()2f x ax ≥+恒成立，求实数a 的取值范围.21.（本小题满分15分）已知椭圆22:132x y C +=，直线:(0)l y kx m m =+≠，设直线l 与椭圆C 相交于,A B 两点.（1）若3m >，求实数k 的取值范围；（2）若直线,,OA AB OB 的斜率成等比数列（其中O 为坐标原点），求OAB ∆的面积的取值范围.22.（本小题满分15分）设数列{}n a 满足2*113,(1)20().n n n a a a a n N +=-++=∈（1）求证：1n a >；（2）求证：12n n a a +<<；（3）设数列{}n a 的前n 项和为n S ，求证：1222()233().23n n n S n -≤-≤-。

2018年杭州市高三年级第一次教学质量检测数学试题卷（文理合卷）考生须知:1. 本卷满分150分, 考试时间120分钟.2. 答题前, 在答题卷密封区内填写学校、班级和姓名.3. 所有答案必须写在答题卷上, 写在试题卷上无效.4. 考试结束, 只需上交答题卷.参考公式如果事件B A ,互斥，那么)()()(B P A P B A P +=+; 如果事件B A ,相互独立，那么)()()(B P A P B A P ⋅=⋅;如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中恰好发生k 次的概率kn kk n n p p C k P --=)1()(.一. 选择题 : 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 . 1．（理科）设z =231i+-, 则z 2 等于 （ ） (A)231i +-. (B) 231i --. (C) 231i +. (D) 231i-. （文科）sin600︒ = ( )(A) –23 (B)–21. (C)23. (D) 21. 2．设A = { x| x ≥ 2}, B = { x | |x – 1|< 3}, 则A ∩B= ( )(A)[2，4] (B)（–∞，–2] (C)[–2，4] (D)[–2，+∞）3．若|a |=2sin150，|b |=4cos150，a 与b 的夹角为300，则a ·b 的值为 ( )(A)23. (B)3. (C)32. (D)21.4．△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，则a cos C+c cos A 的值为 ( )(A)b. (B)2cb +. (C)2cosB. (D)2sinB. 5．一个容量为20的样本数据，分组后，组距与频数如下：则样本在(10 , 50]上的频率为 ( ) (A)201. (B)41. (C)21. (D)107. 6．当x ∈ R 时，令f (x )为sinx 与cosx 中的较大或相等者，设a ≤ f ( x ) ≤ b, 则a + b 等于 ( ) (A)0 (B) 1 +22. (C)1–22. (D)22–1. 7．（理科）设f ( x ) = ax 3 + bx 2 + cx + d, a , b, c, d ∈ R , 又m , n ∈R , m < n ，则下列正确的判断是 （ ）(A) 若f ( m )f ( n ) <0，则f ( x ) = 0在m , n 之间只有一个实根(B) 若f ( m ) f ( n ) > 0，则f ( x ) = 0在m, n 之间至少有一个实根 (C) 若f ( x ) = 0在m , n 之间至少有一个实根，则 f ( m ) f ( n ) < 0 (D) 若f ( m ) f ( n ) > 0, 则f ( x ) =0在m , n 之间也可能有实根 （文科）函数1232)(3+-=x x x f 在区间[0,1]上是（ ） （A ）单调递增的函数. （B ）单调递减的函数. （C ）先减后增的函数 . （D ）先增后减的函数. 8．有80个数，其中一半是奇数，一半是偶数，从中任取两数，则所取的两数和为偶数的概率为 ( )(A)7939. (B)801. (C) 21. (D)8141.9．对于x ∈[0，1]的一切值，a +2b > 0是使ax + b > 0恒成立的（ ）(A)充要条件 (B)充分不必要条件(C)必要不充分条件 (D)既不充分也不必要条件10．设{a n }是等差数列，从{a 1，a 2，a 3，··· ，a 20}中任取3个不同的数，使这三个数仍成等差数列，则这样不同的等差数列最多有（ ）(A)90个 . (B)120个. (C)180个. (D)200个.11．已知函数y = f ( x )（x ∈R ）满足f (x +1) = f ( x – 1)，且x ∈[–1，1]时，f (x) = x 2，则y = f ( x ) 与y = log 5x 的图象的交点个数为 ( )(A)1. (B)2 . (C)3 . (D)4.12．给出下列命题：(1) 若0< x <2π, 则sinx < x < tanx .(2) 若–2π< x< 0, 则sin x < x < tanx.(3) 设A ，B ，C 是△ABC 的三个内角，若A > B > C, 则sinA > sinB > sinC. (4) 设A ，B 是钝角△ABC 的两个锐角，若sinA > sinB > sinC 则A > B > C.. 其中，正确命题的个数是（ ）(A) 4. （B ）3. （C ）2. （D ）1.二. 填空题: 本大题有4小题, 每小题4分, 共16分. 请将答案填写在题中的横线上. 13. 10)21(x +的展开式的第4项是 .14. 某客运公司定客票的方法是：如果行程不超过100km ，票价是0.5元/km ， 如果超过100km ， 超过100km 部分按0.4元/km 定价，则客运票价y 元与行程公里数x km 之间的函数关系式是 . 15. (理科) 在△ABC 中，若3BC AB →-→-⋅=2CA BC →-→-⋅=1ABCA →-→-⋅，则cosA 等于 .（文科）在边长为4的正△ABC 中，→--AB ·→--BC = .16. （理科）已知f ( x )是可导的偶函数，且，则曲线y = f ( x )在（–1，2）处的切线方程是 .（文科）设P 是曲线y = x 2– 1上的动点，O 为坐标原点，当|→--OP |2取得最小值时，点P 的坐标为 . 三. 解答题 :本大题有6小题, 共74分. 解答应写出文字说明, 证明过程或演算步骤. 17. (本小题满分12分)已知命题p: x 2 + mx + 1 = 0有两个不等的负根，命题q ：4x 2 + 4(m – 2 )x + 1 = 0无实根，若命题p 与命题q 有且只有一个为真，求实数m 的取值范围.18．(本小题满分12分)已知}{n a 是等差数列，其前n 项和为S n ，已知a 3=11，S 9=153， （1）求数列}{n a 的通项公式；（2）设n n b a 2log =，证明}{n b 是等比数列，并求其前n 项和T n .19. (本小题满分12分)已知A, B 是△ABC 的两个内角. (1) 若A 、B ∈ (4π, 2π), 求证tanAtanB > 1; (2) 若A, B 满足3cosA = cos(2B –A), 求tan( B – A )tanB 的值.20. (本小题满分12分)A 袋中有1张10元1张5元的钱币，B 袋中有2张10元1张5元的钱币，从A 袋中任取一张钱币与B 袋任取一张钱币互换，这样的互换进行了一次.(理科）求(1) A 袋中10元钱币恰是一张的概率； (2) 设A 袋中的期望金额为a 元，求a . （文科）求（1）A 袋中10元钱币恰是一张的概率；（2）A 袋中10元钱币至少是一张的概率. 21. (本小题满分12分)已知：y = f (x) 定义域为［–1，1］，且满足：f (–1) = f (1) = 0 ，对任意u ,v ∈[–1，1］，都有|f (u) – f (v) | ≤ | u –v | .(1) 判断函数p ( x ) = x 2 – 1 是否满足题设条件？(2) 判断函数g(x)=1,[1,0]1,[0,1]x x x x +∈-⎧⎨-∈⎩，是否满足题设条件？22. (本小题满分14分)已知点P ( t , y )在函数f ( x ) =1x x+(x ≠ –1)的图象上，且有t 2 – c 2at + 4c 2 = 0 ( c ≠ 0 ). (1) 求证：| ac | ≥ 4;(2) 求证：在(–1，+∞）上f ( x )单调递增. (3) (仅理科做）求证：f ( | a | ) + f ( | c | ) > 1.2018年杭州市高三年级第一次教学质量检测数学参考答案一. 选择题 : 本大题共12小题, 每小题5分, 共60分. ） .二. 填空题: 本大题有4小题, 每小题4分, 共16分.13. 960x 3 14. ⎩⎨⎧>+≤≤100104.010005.0x x x x . 15. (理科)63文科）–816. （理科）y = 4x + 6. （文科）(–22, –21）或 (22，–21） . 三. 解答题 :本大题有6小题, 共74分. 解答应写出文字说明, 证明过程或演算步骤. 17. (本小题满分12分)解：∵x 2 + mx + 1 = 0有两个不等的负根，∴⎩⎨⎧<->-0m 04m 2，得m > 2.∵4x 2 + 4(m – 2 )x + 1 = 0无实根， ∴ 16(m – 2 )2 – 16 < 0 , 得 1 < m < 3 . 有且只有一个为真,若p 真q 假，得 m ≥ 3 若p 假q 真，得 1 < m ≤ 2.综合上述得m ≥3,或1< m ≤ 2 .18．(本小题满分12分)解：（1）⎪⎩⎪⎨⎧=⨯+=+153d 289a 911d 2a 11 解得5,31==a d ， 23+=∴n a n .（2）na nb 2=， ∵ 82222b b 3a a a a n 1n n 1n n1n ====-+++ , ∴}b {n 是公比为8的等比数列.又是32211==a b ， ∴)18(73281)81(32T nn n -=--=.19. (本小题满分12分) （1）证：tanAtanB – 1 =B A B A B A cos cos cos cos sin sin -=BA B A cos cos )cos(+-,∵4π< A <2π, 4π< B < 2π,∴2π< A + B < π , ∴ – cos(A + B ) > 0 , cosA > 0, cosB > 0 , ∴ tanAtanB – 1> 0 , 即tanAtanb >1 .（2）解：由3cosA = cos(2B –A),得：3cos[( B – A) – B ] = cos [(B –A) + B ] , ∴3cos(B – A )cosB + 3sin( B – A )sinB = cos( B – A )cosB – sin( B – A)sinB ,即：(1 –3) cos ( B – A)cosB = (3 + 1 )sin( B – A)sinB ,∴ tam( B – A )tanB =3131+-= 3– 2.20. (本小题满分12分)解：（理）（1）A 中2张钱币取1张，有2种情况， B 中3张钱币取1张，有3种情况， ∴互换一次有2⨯3 = 6种情况，其中10元币恰是一张的情况有3种，∴A 袋中10元钱币恰是一张的概率为P 1 =21. （E ξ= 61⨯10 + 63⨯15 + 62⨯20 = 695. 答略（文）（1）同理科.（2）A 袋中恰有一张10元币的概率为P 1 = 21； A 袋中恰有两张10元币的概率为P 2 =31； ∴ A 袋中10元钱币至少是一张的概率P = P 1 + P 2 =31+ 21 = 65. 另解：. A 袋中恰有0张10元币的概率为P 0 =61，∴A 袋中10元钱币至少是一张的概率P = 1 – P 0 = 65. 答略.21. (本小题满分12分)解： (1) 若u ,v ∈ [–1，1]， |p(u) – p (v)| = | u 2 – v 2 |=| (u + v )(u – v) |，取u =43∈[–1，1]，v = 21∈[–1，1], 则 |p (u) – p (v)| = | (u + v )(u – v) | = 45| u – v | > | u – v |，所以p( x)不满足题设条件. （2）分三种情况讨论：10. 若u ,v ∈ [–1，0]，则|g(u) – g (v)| = |(1+u) – (1 + v)|=|u – v |，满足题设条件； 20. 若u ,v ∈ [0，1]， 则|g(u) – g(v)| = |(1 – u) – (1 – v)|= |v –u|，满足题设条件； 30. 若u ∈[–1，0]，v ∈[0，1]，则：|g (u) –g(v)|=|(1 – u) – (1 + v)| = | –u – v| = |v + u | ≤| v – u| = | u –v|，满足题设条件; 40 若u ∈[0，1]，v ∈[–1，0], 同理可证满足题设条件. 综合上述得g(x)满足条件.22. (本小题满分14分)证：(1) ∵ t ∈R, t ≠ –1,∴ ⊿ = (–c 2a)2 – 16c 2 = c 4a 2 – 16c 2 ≥ 0 ， ∵ c ≠ 0, ∴c 2a 2 ≥ 16 , ∴| ac | ≥ 4. (2) 由 f ( x ) = 1 –1x 1+, 法1. 设–1 < x 1 < x 2, 则f (x 2) – f ( x 1) = 1–1x 12+–1 + 1x 11+= )1x )(1x (x x 1221++-. ∵ –1 < x 1 < x 2, ∴ x 1 – x 2 < 0, x 1 + 1 > 0, x 2 + 1 > 0 ,∴f (x 2) – f ( x 1) < 0 , 即f (x 2) < f ( x 1) , ∴x ≥ 0时，f ( x )单调递增. 法2. 由f ` ( x ) =2)1x (1+> 0 得x ≠ –1, ∴x > –1时，f ( x )单调递增.（3）（仅理科做）∵f ( x )在x > –1时单调递增，| c | ≥|a |4> 0 , ∴f (| c | ) ≥ f (|a |4) = 1|a |4|a |4+= 4|a |4+f ( | a | ) + f ( | c | ) = 1|a ||a |++ 4|a |4+> 4|a ||a |++4|a |4+=1.即f ( | a | ) + f ( | c | ) > 1.。

2018年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （ ） A. ∅ B. }2{ C. }5{ D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是A. 902cmB. 1292cmC. 1322cmD. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（ ）A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ） （ ） .60 C D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （ ）A.3≤cB.63≤<cC.96≤<cD. 9>c7.在同意直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（ ）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x y x y x x y≥⎧=⎨<⎩，设,a b r r 为平面向量，则（ ）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2ii ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<< 10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99Λ==i i a i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-=Λ，.3,2,1=k 则 A.321I I I << B. 312I I I << C. 231I I I << D. 123I I I <<二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________. 13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.、在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______ 16.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值19（本题满分14分）已知数列{}n a 和{}n b 满足()()*∈=N n a a a n b n 221Λ.若{}na 为等比数列，且.6,2231b b a +== （1）求n a 与n b ；（2）设()*∈-=N n b a c nn n 11。

浙江省杭州市2018届高三上学期期末考试数学试题选择题部分一、选择题：（本大题共10小题，每小题4分，共40分）1. 设集合，，则（）A. B. C. D.2. 双曲线的渐近线方程为（）A. B. C. D.3. 设数列的通项公式为则“”是“数列为单调递增数列”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4. 若函数的导函数的图像如图所示，则（）A. 函数有1个极大值，2个极小值B. 函数有2个极大值，2个极小值C. 函数有3个极大值，1个极小值D. 函数有4个极大值，1个极小值5. 若直线与曲线（，为自然对数的底数）相切，则（）A. 1B. 2C. -1D. -26. 设不等式组，所表示的区域面积为.若，则（）A. B. C. D.7. 设函数（且）则函数的奇偶性（）A. 与无关，且与无关B. 与有关，且与C. 与有关，且与无关D. 与无关，但与8. 在三棱锥中，平面，，分别是的中点，，且.设与所成角为，与平面所成角为，二面角为，则（）A. B.C. D.9. 设函数，记为函数在上的最大值，为的最大值.（）A. 若，则B. 若，则C. 若，则D. 若，则10. 在四边形中，点分别是边的中点，设，.若，，）A. B.C. D.非选择题部分二、填空题11. 设复数（其中为虚数单位），则复数的实部为__________ ，虚部为__________．12. 在一次随机试验中，事件发生的概率为，事件发生的次数为，则期望__________ ，方差的最大值为__________．13. 在中，角所对的边分别为，，，，则__________ ；设为边上一点，且，则的面积为__________．14. 如图是某三棱锥的三视图，则该三棱锥的体积为__________ ；表面积为__________．15. 在二项式的展开式中，若含的项的系数为-10，则__________．16. 有红，黄，蓝三种颜色的小球（除颜色外均相同）各4只，都分别标有字母．任意取出4只，字母各不相同且三种颜色齐备的取法有__________ 种．17. 已知单位向量的夹角为，设，则当时，的取值范围是__________．三、解答题18. 设向量，，.（Ⅰ）求函数的最小正周期；（Ⅱ）若方程无实数解，求的取值范围.19. 如图，在三棱锥中，，，.（Ⅰ）证明：；（Ⅱ）求与平面所成角的正弦值.20. 设函数.（Ⅰ）求证：；（Ⅱ）当时，函数恒成立，求实数的取值范围.21. 已知椭圆，直线，设直线与椭圆交于两点.（Ⅰ）若，求实数的取值范围；（Ⅱ）若直线的斜率成正等比数列（其中为坐标原点），求的面积的取值范围.22. 设数列满足，.（Ⅰ）求证：；（Ⅱ）求证：；（Ⅲ）设数列的前项和为，求证：.【参考答案】选择题部分一、选择题1. 【答案】C【解析】由集合解得.则故，故选2. 【答案】B【解析】由双曲线得，所以渐近线方程为，故选3. 【答案】A【解析】当时，则数列为单调递增数列若数列为单调递增数列，则即可，所以“”是“数列为单调递增数列”的充分不必要条件故选4. 【答案】B【解析】由导函数图像可知原函数的单调性为先增后减再增再减，最后增，所以原函数有2个极大值，2个极小值，所以选5. 【答案】C【解析】设切点坐标为，，，则切线方程为，又因为切线为过代入得，将代入中得故选6. 【答案】A【解析】如图：当与交点为时面积为，此时，若则故选7. 【答案】D【解析】由函数则当时函数为奇函数，当时函数为非奇非偶函数所以函数的奇偶性与无关，但与有关故选8. 【答案】A【解析】如图可知，，因为平面则，又由，故，则，同理可证得所以故选9. 【答案】C【解析】由题意得，则若，则，此时任意有则，，，在时与题意相符，故选10. 【答案】D【解析】又点分别是边的中点，所以，两式相加得，两边同时平方得，所以则，代入得即，故选.非选择题部分二、填空题11.【答案】2 1【解析】所以复数的实部为，虚部为12.【答案】【解析】记事件发生的次数为可能的值为期望方差故期望，方差的最大值为13.【答案】2【解析】由得，，又因为，则点为边上靠近点的三等分点，14. 【答案】【解析】还原几何体如图：根据图中数据可得：15.【答案】-2【解析】二项式通项，当的项的系数为时，即解得，则所以16.【答案】36【解析】字母各不相同且三种颜色齐备则分别取出个小球，共有点睛：本题考查了排列组合，要满足题目中“字母各不相同且三种颜色齐备”先理清可能性，然后运用组合法求出数量后除去重复的可能，再进行全排列，即可计算出结果17.【答案】【解析】，所以，不妨令，原式，当时当时所以的取值范围是三、解答题18. 解：（Ⅰ）因为，故的最小正周期为.（Ⅱ）若方程无解，则，所以或，由解得或；由，故不等式无解，所以或.19. （Ⅰ）证明：∵，，，∴，取的中点，连接，则，，又，∴平面，∴.（Ⅱ）解：在中，根据余弦定理，得，所以，又因为，所以，，所以，即.则以为轴，为轴，为轴，建立坐标系，则，，，.所以，，.设平面的法向量为，则，取，则，即与平面所成的角正弦值为.20. （Ⅰ）证明：原不等式等价于，设，所以，当时，，单调递减；当时，，单调递增.又因为，所以.所以.（Ⅱ）解：当时，恒成立，即恒成立.当时，；当时，而，所以.21. 解：（Ⅰ）联立方程和，得，所以，所以，所以，即，解得或.（Ⅱ）设，，则，，设直线的斜率，因为直线的斜率成等比数列，所以，即，化简，得，即.因为，原点到直线的距离所以，当时，直线或的斜率不存在，等号取不到，所以.22. 证明：（Ⅰ）整理得，因为，故.（Ⅱ）又因为，因为，所以与同号，所以与同号，因为，所以，那么，则，所以.（Ⅲ）由（Ⅱ）知，故，因为，所以，故，所以，不等式三边同时求和，得，所以.。