三角形-星形(△-Y)等效变换公式的巧妙证明

三角形和星形电阻电路的等效变换在咱们日常的电子学世界里，遇到那些复杂的电阻电路，比如那个三角形和星形电阻组合起来的小玩意儿，可真是让人头疼。

不过别急，今天咱们就来聊聊这个“三角”与“星”的奇妙关系，让你轻松搞定这些电路的等效变换问题。

首先得明白，三角形电阻和星形电阻虽然长得像，但它们的工作原理和特点可是大不相同。

三角形电阻就像是三根并排的电线，而星形电阻则是中间那根电线特别粗，两边细得像星星一样。

这俩家伙各有千秋，用在不同的场合效果也不一样。

咱们先说说三角形电阻吧。

它就像是一个等边三角形，三条边的长度完全一样。

这种电阻的特点是稳定性好，误差小，而且它的电阻值是固定的，不会因为电压的变化而改变。

想象一下，如果你要测量一个精确的电阻值，那么三角形电阻绝对是你的首选。

再说说星形电阻。

它的形状就像一个星星，中间的那根线比其他两根粗很多。

这种电阻的特点是响应速度快，但是稳定性差一些。

因为它的电阻值会随着电流的变化而变化，所以不适合用来做那种需要精确电阻值的场合。

现在咱们来说说如何把这两个小家伙变成好朋友。

这就需要用到一个叫做“串联”的魔法。

简单来说，就是把两个或者更多个电阻器连接在一起，它们会共享相同的电流，但是各自承担不同的电压。

这样一来，整个电路的电压就变成了原来的两倍或者三倍，这就是所谓的串联。

但是，如果只是简单地把三角形电阻和星形电阻串联起来，可能会遇到一个问题——那就是总电阻值变大了。

这时候怎么办呢？别担心，我们还有一个“并联”的魔法可以救场。

简单来说，就是把两个或者更多个电阻器连接在一起，它们会共享相同的电压，但是各自承担不同的电流。

这样一来，整个电路的总电流就变成了原来的一半或者三分之一，这就是所谓的并联。

通过串联和并联的操作，我们可以让三角形电阻和星形电阻组成一个完整的电路。

这样，无论你想要测量的是电压、电流还是电阻，这个电路都能帮你搞定。

而且，由于它们各自的特性被巧妙地利用起来，整个电路的性能也会得到提升。

电阻网络中的三角形星形等效变换解析实例电阻网络中的三角形-星形等效变换解析实例在电路分析中，等效变换是一种将复杂电路简化成简单电路的方法。

其中，三角形-星形等效变换是常用的一种方法，可以将电阻网络中的三角形形式转换为星形形式，使得电路的计算更加简便。

本文将通过几个实例来解析电阻网络中的三角形-星形等效变换，以展示这一方法的应用。

实例一：在如下电阻网络中，我们希望将三角形形式转换为星形形式：R1 R2 R3o--------o-----------o-----------o| | |RL R5 R6| | |o--------o-----------o-----------oR4 R7 R8首先，我们按照以下步骤进行等效变换：1. 将RL与R1进行并联，得到RL1；2. 将RL1与R7进行并联，得到RL2；3. 将R4与RL2进行并联，得到RL3；4. 将R5与RL3进行并联，得到RL4。

经过以上等效变换后，得到如下的星形形式电路：RL4 RL3 RL2o--------o-----------o-----------o| | |R2 R3 R8| | |o--------o-----------o-----------oR1 R5 R6通过以上变换，我们成功将电阻网络转换为了星形形式，从而简化了电路的计算。

实例二：现在考虑一个稍为复杂的电阻网络，其中包含多个三角形形式的电阻网络。

我们希望将整个电路转换为星形形式。

R2 R3o--------o----------------------o|R1 L|o|RL R4 RL|R5 L|o|R6 R7o ----------------------o----------------o为实现等效变换，我们按照以下步骤进行处理：1. 将RL与R1进行并联，得到RL1；2. 将RL1与R4进行并联，得到RL2；3. 将RL2与R5进行并联，得到RL3；4. 将R6与RL3进行并联，得到RL4；5. 将RL4与R3进行并联，得到RL5；6. 将RL5与R7进行并联，得到RL6。

三角形和星形电阻电路的等效变换三角形和星形电阻电路的等效变换，这个话题听起来好像有点高深莫测，但其实它就像是我们日常生活中的一道数学题目。

今天，我就来给大家讲讲这道题目的答案，希望能够帮助大家更好地理解这个概念。

我们来看看三角形电阻电路。

三角形电阻电路是指由三个电阻器组成的电路，这三个电阻器的阻值可以不同。

当我们把这三个电阻器连接在一起时，就会形成一个三角形。

那么，这个三角形电阻电路有什么特点呢？三角形电阻电路的特点就是它的电流分布是均匀的。

这是因为在三角形中，每个顶点都是一个交点，而根据欧姆定律，电流通过交点时会受到阻碍。

所以，当三个电阻器的阻值不它们所承受的电流也会不同。

但是，由于三角形的结构特点，这些电流会被平均分配到每个顶点上，从而使得整个电路的电流分布变得均匀起来。

接下来，我们再来看看星形电阻电路。

星形电阻电路是指由一个电阻器和一个电源组成的电路，这个电阻器的阻值很小，可以忽略不计。

那么，这个星形电阻电路有什么特点呢？星形电阻电路的特点就是它的电流只从正极流向负极。

这是因为在星形结构中，电源的一端连接着一个很小的电阻器，而另一端则直接连接到了负载上。

由于这个小电阻器的阻值很小，所以它对整个电路的影响可以忽略不计。

因此，在星形结构中，电流只会沿着一个方向流动，即从正极流向负极。

那么，如何将这两个电路进行等效变换呢？其实很简单，只需要把三角形电阻电路中的三个电阻器分别替换成一个星形电阻器和两个相同的较小电阻器就可以了。

这样一来，原来的三角形电阻电路就变成了一个由一个星形电阻器和两个相同的较小电阻器组成的新的电路。

这个新的电路的特点是什么呢？这个新的电路的特点就是它的电流分布仍然是均匀的。

这是因为在这个新的电路中，虽然只有一个星形电阻器和两个相同的较小电阻器组成了负载部分，但是由于这两个较小的电阻器的阻值相同且很小，所以它们对整个负载的影响也可以忽略不计。

因此，在整个负载部分中仍然存在着类似于三角形电阻电路中的均匀电流分布情况。

电阻星形连接与三角形连接的等效变换公式在电路中，电阻是一个常见的元件，用于限制电流的流动。

而电阻的连接方式有很多种，其中包括星形连接和三角形连接。

这两种连接方式在电路中起到了不同的作用，我们可以通过等效变换公式来分析它们之间的关系。

我们来看一下电阻星形连接。

在电阻星形连接中，三个电阻被连接在一起，形成一个类似于星形的形状。

这种连接方式常用于需要将多个电阻连接到同一个节点的情况。

对于电阻星形连接，我们可以使用等效变换公式来计算其总电阻。

假设三个电阻分别为R1、R2和R3，它们之间的等效电阻为Re。

根据等效变换公式，我们可以得到以下等式：1/Re = 1/R1 + 1/R2 + 1/R3换句话说，电阻星形连接的总电阻等于三个电阻的倒数之和的倒数。

这个公式可以帮助我们快速计算电阻星形连接的总电阻。

接下来，我们来看一下电阻三角形连接。

在电阻三角形连接中，三个电阻被连接在一起，形成一个类似于三角形的形状。

这种连接方式常用于需要将多个电阻连接在一起并形成闭合电路的情况。

对于电阻三角形连接，我们同样可以使用等效变换公式来计算其总电阻。

假设三个电阻分别为R1、R2和R3，它们之间的等效电阻为Re。

根据等效变换公式，我们可以得到以下等式：Re = R1 + R2 + R3换句话说，电阻三角形连接的总电阻等于三个电阻的和。

这个公式同样可以帮助我们快速计算电阻三角形连接的总电阻。

通过比较电阻星形连接和电阻三角形连接的等效变换公式，我们可以看出它们之间的区别。

在电阻星形连接中，总电阻等于三个电阻的倒数之和的倒数；而在电阻三角形连接中，总电阻等于三个电阻的和。

这意味着，在相同的电阻值下，电阻星形连接的总电阻要小于电阻三角形连接的总电阻。

这种差异在实际电路设计中是非常重要的。

通过选择合适的电阻连接方式，我们可以有效地控制电路的总电阻，从而实现所需的电流或电压分配。

在一些特殊的应用中，选择不同的电阻连接方式还可以帮助我们实现特定的电路功能或优化电路性能。

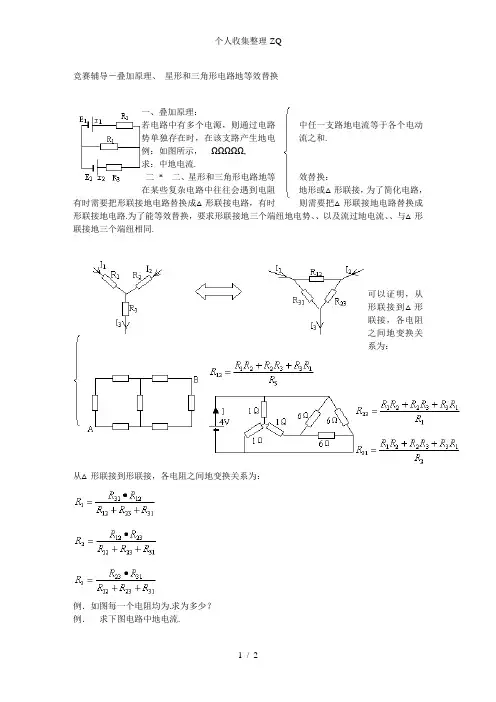
竞赛辅导－叠加原理、 星形和三角形电路地等效替换
一、叠加原理：
若电路中有多个电源，则通过电路中任一支路地电流等于各个电动
势单独存在时，在该支路产生地电流之和.
例：如图所示， ΩΩΩΩΩ,
求：中地电流.
二 * 二、星形和三角形电路地等效替换：
在某些复杂电路中往往会遇到电阻地形或△形联接，为了简化电路，
有时需要把形联接地电路替换成△形联接电路，有时则需要把△形联接地电路替换成形联接地电路.为了能等效替换，要求形联接地三个端纽地电势、、以及流过地电流、、与△形联接地三个端纽相同.
可以证明，从
形联接到△形
联接，各电阻
之间地变换关
系为：
从△形联接到形联接，各电阻之间地变换关系为：
例．如图每一个电阻均为.求为多少？
例． 求下图电路中地电流.。

电阻网络中的三角形星形等效变换解析引言:电阻网络是电路分析中常见的一种形式，使用电阻、电源和连接线将电路元件组装在一起。

在电路分析中，对于复杂的电阻网络，我们经常需要简化电路结构以便更方便地进行计算和分析。

其中一种常见的简化方法就是进行等效变换。

一、三角形到星形等效变换1. 三角形等效变换的原理在电阻网络中，当使用三个电阻相互连接而成三角形时，我们可以通过将三角形转换为星形来简化电路结构。

这种等效变换的原理是基于KCL（电流守恒定律）。

根据KCL，三角形中的每个节点的电流总和为零。

因此，我们可以通过连接三角形中的节点中间电路的电阻，将三角形转换为星形。

2. 三角形到星形等效变换的公式在进行三角形到星形等效变换时，我们需要计算三角形电阻与星形电阻的关系。

假设三角形电阻分别为R1、R2和R3，星形电阻分别为Rab、Rbc和Rca，则它们之间的关系为：1/Rab = 1/R1 + 1/R2 + 1/R31/Rbc = 1/R1 + 1/R2 + 1/R31/Rca = 1/R1 + 1/R2 + 1/R33. 三角形到星形等效变换的实例以一个简单的三角形电阻网络为例，假设三角形中的三个电阻分别为10Ω、20Ω和30Ω。

我们来计算它们的星形等效电阻。

根据上述公式，我们可以得到：1/Rab = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rbc = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rca = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/60通过求倒数，并计算总电阻，我们可以得到星形电阻的数值为：Rab = 60/7 ΩRbc = 60/7 ΩRca = 60/7 Ω二、星形到三角形等效变换1. 星形等效变换的原理与三角形到星形等效变换相反，我们可以通过将星形转换为三角形来简化电路结构。

星形电路与三角形电路等效变换公式的简便方法摘要：介绍导出星形电路与三角形电路等效变换公式的一种简便方法关键词：星形电路三角形电路等效变换星形电路与三角形电路间的等效变换（简称Y—△等效变换）是电路分析和计算过程中经常需用到的一种变换。

因变换公式推导过程复杂，故在解决有关问题时，人们通常直接套用有关公式。

然而，由于变换公式形式比较繁锁，记忆不便，每次计算通常都需查找电路方面的有关书籍，给Y—△等效变换带来了不便。

最近有人已进行了一些研究，试图解决这一问题。

在本文中，作者提出了一种导出Y—△等效变换公式的简便方法。

利用该法，可非常迅速地写出Y—△等效变换公式，给电路的Y—△等效变换带来了方便。

为了说明本文方法，先以电阻电路为例，列写出Y—△等效变换公式。

设图1（a）和图1（b）两电路互为等效电路，则两电路的电阻间存在以下关系。

R1= （1）R2= （2）R3= （3）R12= + + （4）R23= + + （5）R31= + +（6）若星形电路的三个电阻相等，即R1= R2 =R3= RY，则等效的三角形电路有三个电阻也相等，即R12= R23 =R31= R△。

将这些关系停薪留职入（1）式和（4）式可得RY= R△（7）R△=3RY （8）以上（1）—（8）式即为Y—△等效变换用到的有关公式。

本文提出的导出上述各公式的方法是首先通过对称Y形和△形电路导出（7）、（8）两式，然后根据Y—△等效变换公式的基本形式对（7）、（8）两式进行变化，最后利用电路元件位置的对称性，通过变化了的（7）、（8）两式直接写出（1）—（6）式。

下面介绍这一方法。

设图2（a）和图2（b）互为等效电路，从两电路的1端流入的电流均为I，并且该电流分为两等份分别从2、3端流出。

因图2（a）和图2（b）互为等效电路，故两电路的1、2端间的电压相等，所以有RYI+RY• I=R△• I（9）由此得RY= R△（10）这样即导出了（7）式，根据Y—△等效变换公式的基本形式，可将（10）式变为RY= = （11）设上式中RY为星形电路1端所接电阻R1，则上式等号右边分子上的两个电阻R△必为三角形电路中相对1端位置成对称关系的两个电阻R12、R31，而分母为三角形电路中的三个电阻，必为R12、R12、R31、，这样由（11）式可导出R1=（12）以上即为（1）式。

三角形和星形电阻电路的等效变换嘿，伙计们！今天我们要聊聊一个非常有趣的话题：三角形和星形电阻电路的等效变换。

你们知道吗，这个话题可是让我们这些电子工程师头疼不已啊！但是，别担心，我会用最简单的语言来解释这个问题，让你们轻松理解。

我们来看看什么是三角形电阻电路。

三角形电阻电路是指由三个电阻器组成的电路，它们按照一定的顺序连接在一起。

而星形电阻电路呢？星形电阻电路是指由一个电阻器和它的两个相邻的电阻器组成的电路，这三个电阻器按照星形排列。

那么，为什么我们需要研究三角形和星形电阻电路的等效变换呢？原因很简单，因为这两种电路在很多情况下是相似的，我们可以通过一种方法来简化它们的计算。

这就是我们今天要讨论的主题：如何将三角形电阻电路转换为星形电阻电路。

我们要明确一点：无论是三角形电阻电路还是星形电阻电路，它们的总阻抗都是相同的。

这是因为总阻抗是由各个元件的阻值和它们之间的连接方式决定的。

所以，我们只需要找到一种方法，使得三角形电阻电路的总阻抗与星形电阻电路的总阻抗相等即可。

那么，这种方法究竟是什么呢？其实，它就是利用基尔霍夫定律(KCL)和基尔霍夫电压定律(KV)。

基尔霍夫定律告诉我们，在一个封闭的回路中，各个分支电流之和等于零；而基尔霍夫电压定律告诉我们，在一个封闭的回路中，各个分支电压之和等于零。

现在，我们可以开始进行等效变换了。

我们要用基尔霍夫定律来找出三角形电阻电路中的各个分支电流。

然后，我们再用基尔霍夫电压定律来找出星形电阻电路中的各个分支电压。

我们可以根据这两个结果来建立一个等效方程组，从而得到三角形电阻电路的总阻抗与星形电阻电路的总阻抗之间的关系。

通过这个等效变换，我们就可以把复杂的三角形电阻电路简化为一个简单的星形电阻电路。

这样一来，我们就可以用更简单的方法来计算它们的总阻抗了。

这对于我们的电子工程师来说，可是一个非常有用的技巧啊！好了，今天的分享就到这里啦！希望我用简单的语言和生动的例子帮助大家理解了三角形和星形电阻电路的等效变换。

三角形变星形公式三角形变星形公式是指在平面上，通过连接三个顶点，正好形成一个三角形的情况。

然而，在实际生活和数学问题中，人们也经常需要处理类似于星形的图形，这些图形由多条线段或线段的延长线组成。

在本文中，我们将介绍一种方法来将一个三角形变换为一个星形。

具体而言，我们将讨论如何通过对三角形进行角度、边长和位置的变换来得到一个星形。

首先，让我们考虑一个等边三角形，边长为a。

等边三角形的每个内角都是60度。

为了将等边三角形变换为星形，我们可以从每个顶点开始，将边长延长到一定的长度，然后连接这些延长线的交点，形成一个星形。

首先，让我们以A、B和C代表等边三角形的三个顶点。

从顶点A开始，我们将边a延长一定的长度，连接延长线与边BC的交点为D。

同样地，我们从顶点B延长边a，与边AC的交点为E。

最后，用类似的方式，我们从顶点C延长边a，与边AB的交点为F。

连接点D、E和F，得到一个新的图形，称为星形。

这个星形拥有六条线段，分别是AD、BE、CF、DE、EF和FD。

这六条线段的组合形成了一个星形。

现在，让我们来计算这个星形的形状。

我们首先需要计算每个角的大小，以确定星形的内部结构。

根据等边三角形的性质，三个内角均为60度。

同时，我们可以看到，星形由六个三角形组成，每个三角形的两个角是等边三角形的一个内角。

因此，星形的每个内角都是120度。

接下来，我们将计算星形的边长。

我们已经知道星形由六条边组成，其中两条边的长度与等边三角形的边长相同。

因此，这两条边的长度是a。

另外，我们还可以看到星形的另外四条边实际上是标准等边三角形中的两个边长度的两倍。

因此，这四条边的长度为2a。

最后，我们来确定星形的位置。

星形的中心点可以通过连接等边三角形的各个顶点并求交点得到。

这个交点将位于星形的重心位置。

同时，我们可以观察到星形的每条边都与等边三角形中的一条边对齐，并且都与另外两条交于一点。

这些交点将位于星形的重心位置。

因此，星形的重心将位于等边三角形的重心位置。

电阻的星型与三角形的等效变换例题在电路中，电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。

通过将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，可以简化电路分析过程，使得问题更容易解决。

在本文中，我们将深入探讨电阻的星型与三角形的等效变换，以帮助读者更好地理解这一概念。

1. 电阻的星型与三角形的等效变换概述在电路分析中，星型电阻网络由三个电阻分支组成，形状类似于星型，而三角形电阻网络由三个电阻分支组成，形状类似于三角形。

当需要对这样的电阻网络进行分析时，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，从而简化电路分析的复杂度。

2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。

通过合并相邻的电阻，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络。

这种等效变换的原理在于保持电路中的等效电阻值不变，从而简化电路分析的过程。

3. 电阻的星型与三角形的等效变换例题分析举例来说，对于一个星型电阻网络，我们可以按照以下步骤将其转换为等效的三角形电阻网络：- 合并星型电阻网络中的相邻电阻，得到等效的三角形电阻网络；- 计算等效的三角形电阻网络的总电阻值。

类似地，对于一个三角形电阻网络，我们可以按照以下步骤将其转换为等效的星型电阻网络：- 合并三角形电阻网络中的相邻电阻，得到等效的星型电阻网络；- 计算等效的星型电阻网络的总电阻值。

通过以上步骤，我们可以将星型与三角形电阻网络之间进行等效变换，从而简化电路分析的过程。

4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中，电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。

以电子电路设计为例，当需要对复杂的电路进行分析与设计时，可以利用星型与三角形的等效变换，将复杂的电路结构简化为更容易分析的形式，从而提高电路设计的效率与精度。