电阻星形连接与三角形连接的等效变换

电阻三角形和星形变换公式
电阻三角形变换公式是指在一个三角形电路中，将三角形的三个电阻分别用它们两两并联的等效电阻替代时所得到的等效电路。

设三角形电路的三条边上的电阻分别为R1、R2、R3，其等效电路中的电阻为Req，则电阻三角形变换公式为：1/Req = 1/R1 + 1/R2 + 1/R3。

电阻星形变换公式是指在一个星形电路中，将星形电路中的三个电阻分别用它们两两串联的等效电阻替代时所得到的等效电路。

设星形电路中的三个电阻分别为R1、R2、R3，其等效电路中的电阻为Req，则电阻星形变换公式为：1/Req = 1/R1 + 1/R2 + 1/R3。

三角形和星形电阻电路的等效变换三角形和星形电阻电路的等效变换，这个话题听起来好像有点高深莫测，但其实它就像是我们日常生活中的一道数学题目。

今天，我就来给大家讲讲这道题目的答案，希望能够帮助大家更好地理解这个概念。

我们来看看三角形电阻电路。

三角形电阻电路是指由三个电阻器组成的电路，这三个电阻器的阻值可以不同。

当我们把这三个电阻器连接在一起时，就会形成一个三角形。

那么，这个三角形电阻电路有什么特点呢？三角形电阻电路的特点就是它的电流分布是均匀的。

这是因为在三角形中，每个顶点都是一个交点，而根据欧姆定律，电流通过交点时会受到阻碍。

所以，当三个电阻器的阻值不它们所承受的电流也会不同。

但是，由于三角形的结构特点，这些电流会被平均分配到每个顶点上，从而使得整个电路的电流分布变得均匀起来。

接下来，我们再来看看星形电阻电路。

星形电阻电路是指由一个电阻器和一个电源组成的电路，这个电阻器的阻值很小，可以忽略不计。

那么，这个星形电阻电路有什么特点呢？星形电阻电路的特点就是它的电流只从正极流向负极。

这是因为在星形结构中，电源的一端连接着一个很小的电阻器，而另一端则直接连接到了负载上。

由于这个小电阻器的阻值很小，所以它对整个电路的影响可以忽略不计。

因此，在星形结构中，电流只会沿着一个方向流动，即从正极流向负极。

那么，如何将这两个电路进行等效变换呢？其实很简单，只需要把三角形电阻电路中的三个电阻器分别替换成一个星形电阻器和两个相同的较小电阻器就可以了。

这样一来，原来的三角形电阻电路就变成了一个由一个星形电阻器和两个相同的较小电阻器组成的新的电路。

这个新的电路的特点是什么呢？这个新的电路的特点就是它的电流分布仍然是均匀的。

这是因为在这个新的电路中，虽然只有一个星形电阻器和两个相同的较小电阻器组成了负载部分，但是由于这两个较小的电阻器的阻值相同且很小，所以它们对整个负载的影响也可以忽略不计。

因此，在整个负载部分中仍然存在着类似于三角形电阻电路中的均匀电流分布情况。

电阻星形连接与三角形连接的等效变换公式在电路中，电阻是一个常见的元件，用于限制电流的流动。

而电阻的连接方式有很多种，其中包括星形连接和三角形连接。

这两种连接方式在电路中起到了不同的作用，我们可以通过等效变换公式来分析它们之间的关系。

我们来看一下电阻星形连接。

在电阻星形连接中，三个电阻被连接在一起，形成一个类似于星形的形状。

这种连接方式常用于需要将多个电阻连接到同一个节点的情况。

对于电阻星形连接，我们可以使用等效变换公式来计算其总电阻。

假设三个电阻分别为R1、R2和R3，它们之间的等效电阻为Re。

根据等效变换公式，我们可以得到以下等式：1/Re = 1/R1 + 1/R2 + 1/R3换句话说，电阻星形连接的总电阻等于三个电阻的倒数之和的倒数。

这个公式可以帮助我们快速计算电阻星形连接的总电阻。

接下来，我们来看一下电阻三角形连接。

在电阻三角形连接中，三个电阻被连接在一起，形成一个类似于三角形的形状。

这种连接方式常用于需要将多个电阻连接在一起并形成闭合电路的情况。

对于电阻三角形连接，我们同样可以使用等效变换公式来计算其总电阻。

假设三个电阻分别为R1、R2和R3，它们之间的等效电阻为Re。

根据等效变换公式，我们可以得到以下等式：Re = R1 + R2 + R3换句话说，电阻三角形连接的总电阻等于三个电阻的和。

这个公式同样可以帮助我们快速计算电阻三角形连接的总电阻。

通过比较电阻星形连接和电阻三角形连接的等效变换公式，我们可以看出它们之间的区别。

在电阻星形连接中，总电阻等于三个电阻的倒数之和的倒数；而在电阻三角形连接中，总电阻等于三个电阻的和。

这意味着，在相同的电阻值下，电阻星形连接的总电阻要小于电阻三角形连接的总电阻。

这种差异在实际电路设计中是非常重要的。

通过选择合适的电阻连接方式，我们可以有效地控制电路的总电阻，从而实现所需的电流或电压分配。

在一些特殊的应用中，选择不同的电阻连接方式还可以帮助我们实现特定的电路功能或优化电路性能。

星三角电阻转换公式
星三角电阻转换公式是指将三个电阻呈三角形连接的电路转换成呈星型连接的电路时，所需使用的公式。

这个公式可以表示为：RAB = (RA*RB+ RB*RC +RC*RA)/(RC)
其中，RAB是星型电路中A和B之间的等效电阻，RA、RB和RC分别是三角形电路中三个电阻的阻值。

这个公式可以用来计算星型电阻和三角形电阻之间的等效电阻，这样就可以将一种电路拓扑结构转换成另一种，以方便电路设计和分析。

此外，星型电阻和三角形电阻的等效电阻还可以通过其他方法来计算，例如使用矩阵方法或毕奥定理等。

这些方法都可以为工程师和设计师提供准确的电路计算结果。

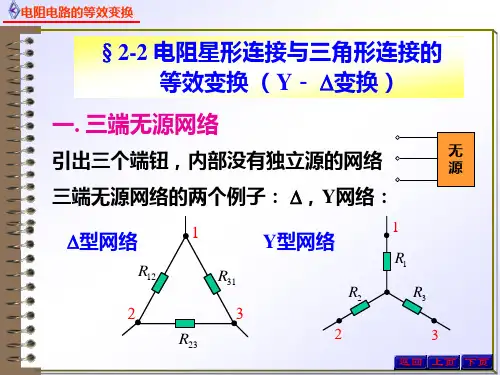
电阻的星形和三角形连接的等效变换之马矢奏春创作1、电阻的星形和三角形连接三个电阻元件首尾相连接，连成一个封闭的三角形，三角形的三个顶点接到外部电路的三个节点，称为电阻元件的三角形连接简称△连接，如图 2.7（a ）所示。

三个电阻元件的一端连接在一起，另一端分别连接到外部电路的三个节点，称为电阻元件的星形连接，简称Y 形连接，如图2.7（b ）所示。

三角形连接和星形连接都是通过三个节点与外部电路相连，它们之间的等效变换是要求它们的外部特性相同，也就是当它们的对应节点间有相同的电压12U 、23U 、31U 时，从外电路流入对应节点的电流1I 、2I 、3I 也必须分别相等，即Y-△变换的等效条件。

一种简单的推导等效变换方法是：在一个对应端钮悬空的同等条件下，分别计算出其余两端钮间的电阻，要求计算出的电阻相等。

悬空端钮3时，可得：12233112122331()R R R R R R R R ++=++ 悬空端钮2时，可得：31122331122331()R R R R R R R R ++=++悬空端钮1时，可得：23123123122331()R R R R R R R R ++=++ 联立以上三式可得：123111223311223212233131233122331R R R R R R R R R R R R R R R R R R =++=++=++ （2-2）式（2-2）是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。

从式（2-2）可解的：121212323232313131312R R R R R R R R R R R R R R R R R R =++=++=++ （2-3）以上互换公式可归纳为：当Y 形连接的三个电阻相等时，即123Y R R R R ===,则等效△形连接的三个电阻也相等，它们等于1223313Y R R R R R ∆==== 或 1=3Y R R ∆ （2-4）。

电阻网络中的星形三角形变换分析在电阻网络中，星形和三角形连接是常见的连接方式。

这两种连接方式在电路分析和设计中具有重要的作用。

本文将对电阻网络中的星形三角形变换进行详细分析，以帮助读者更好地理解和应用这一概念。

一、星形连接和三角形连接简介1. 星形连接在电路中，星形连接是指将三个或更多的电阻连接在一起，其中一个节点连接到电源正极，其余节点连接到电源负极。

这种连接方式常用于电路中需要提供共地或共点的情况。

2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。

三角形连接常用于电路中需要提供平衡电路或无共地的情况。

二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。

通过执行星形三角形变换，可以简化电路的分析和计算。

具体变换原理如下：1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。

设星形连接的电阻为R1，R2，R3，其中节点A连接到电源正极，节点B和C连接到电源负极。

则等效的三角形连接电阻可表示为：RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。

设三角形连接的电阻为RT，RA，RB，其中节点A、B、C两两相连，形成闭合的三角形。

则等效的星形连接电阻可表示为：R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用，其中包括但不限于以下几个方面：1. 简化电路分析和计算通过执行星形三角形变换，可以将复杂的电路转换为等效的简化电路，从而简化电路的分析和计算。

这种方法尤其适用于涉及大量电阻和复杂连接的电路。

电阻网络中的三角形星形等效变换解析引言:电阻网络是电路分析中常见的一种形式，使用电阻、电源和连接线将电路元件组装在一起。

在电路分析中，对于复杂的电阻网络，我们经常需要简化电路结构以便更方便地进行计算和分析。

其中一种常见的简化方法就是进行等效变换。

一、三角形到星形等效变换1. 三角形等效变换的原理在电阻网络中，当使用三个电阻相互连接而成三角形时，我们可以通过将三角形转换为星形来简化电路结构。

这种等效变换的原理是基于KCL（电流守恒定律）。

根据KCL，三角形中的每个节点的电流总和为零。

因此，我们可以通过连接三角形中的节点中间电路的电阻，将三角形转换为星形。

2. 三角形到星形等效变换的公式在进行三角形到星形等效变换时，我们需要计算三角形电阻与星形电阻的关系。

假设三角形电阻分别为R1、R2和R3，星形电阻分别为Rab、Rbc和Rca，则它们之间的关系为：1/Rab = 1/R1 + 1/R2 + 1/R31/Rbc = 1/R1 + 1/R2 + 1/R31/Rca = 1/R1 + 1/R2 + 1/R33. 三角形到星形等效变换的实例以一个简单的三角形电阻网络为例，假设三角形中的三个电阻分别为10Ω、20Ω和30Ω。

我们来计算它们的星形等效电阻。

根据上述公式，我们可以得到：1/Rab = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rbc = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/601/Rca = 1/10 + 1/20 + 1/30 = 3/60 + 2/60 + 2/60 = 7/60通过求倒数，并计算总电阻，我们可以得到星形电阻的数值为：Rab = 60/7 ΩRbc = 60/7 ΩRca = 60/7 Ω二、星形到三角形等效变换1. 星形等效变换的原理与三角形到星形等效变换相反，我们可以通过将星形转换为三角形来简化电路结构。

一、基础知识和基础理论1.1交流电路电压电流关系1.2电阻星形连接与三角形连接等效变换公式：1.3电路分析的基本方法（1）克希荷夫第一定律（克希荷夫电流定律KCL)：在电路任何时刻，对任一结点，所有支路电流的代数和恒等于零，即流出结点的取+号，流入结点的取-号.N为支路数。

(2)克希荷夫第二定律（克希荷夫电压定律KVL）:在电路任何时刻，沿任一回路，所有支路电压的代数和恒等于零，即电压的参考方向与指定的绕行方向一致的取+号,相反的取—号。

N为支路数。

(3）支路电流法：应用KCL、KVL列出与支路电流数目相等的方程,求解支路电流的方法. （4）回路电流法。

（5)结点电压法:对于有几个结点的电路，任选一个结点作为参考点,其余点相对于参考点的之间的电压为结点电压，以结点电压为未知量，应用KVL列出（民N—1）个独立结点电压方程。

（6)叠加定理：在线性电路中，任一支路的电压或电流都是各个独立源单独作用于电路时，在该支路产生的电压或电流的代数和.（7）戴维南定理:任何有源二端线性网络，可用一个电压源和一个电阻的串联组合等效替代.其中电动势等于有源二端网络的开路电压U0,电阻为端口内部电源为0零时的开端电阻。

（8）诺顿定理：任何有源二端线性网络,可用一个电流源和一个电阻的并联组合等效替代。

其中电流源等于有源端口的短路电流I0,电阻为端口内部电源为0零时的开端电阻。

1。

4运算电路的输入输出电压关系1。

5调制：在发送端利用低频信号去控制高频信号的某一个参数，使高频信号的该参数按照低频信号的变化规律而变化的过程.调幅、调频、调相。

调制信号有模拟和数字信号。

解调:将低频信号从调制信号中分离的过程。

1。

6电力变压器的额定容量：变压器二次侧额定输出功率，或称视在功率新系列R10系列为30，50,63，80，100,125，160，200,250，315，400,500,630，。

额定电压指相线电压。

额定电流：二次侧额定输出时，一次或二次侧流过的电流称为一次或二侧的额定电流。

电阻星形连接与三角形连接的等效变换公式一、电阻星形连接的等效变换公式在电路中，星形连接是指将三个电阻分别连接在一个共节点上，形成一个星形的连接方式。

在星形连接中，我们可以通过等效变换将星形连接转换为三角形连接。

设电阻A、B、C分别为星形连接中的三个电阻，它们与共节点的连线分别为AB、AC、BC。

根据星形连接的特性，我们可以得到以下关系式：1/RA = 1/AB + 1/AC1/RB = 1/AB + 1/BC1/RC = 1/AC + 1/BC根据以上关系式，我们可以推导出电阻星形连接的等效变换公式：1/RA = 1/R1 + 1/R2 + 1/R31/RB = 1/R1 + 1/R2 + 1/R31/RC = 1/R1 + 1/R2 + 1/R3其中，R1、R2、R3分别为星形连接中的三个电阻。

二、电阻三角形连接的等效变换公式与电阻星形连接相反，电阻三角形连接是指将三个电阻分别两两相连，形成一个三角形的连接方式。

在三角形连接中，我们可以通过等效变换将三角形连接转换为星形连接。

设电阻X、Y、Z分别为三角形连接中的三个电阻，它们之间的连线分别为XY、XZ、YZ。

根据三角形连接的特性，我们可以得到以下关系式：1/RX = 1/XY + 1/XZ1/RY = 1/XY + 1/YZ1/RZ = 1/XZ + 1/YZ根据以上关系式，我们可以推导出电阻三角形连接的等效变换公式：1/RX = 1/RA + 1/RB + 1/RC1/RY = 1/RA + 1/RB + 1/RC1/RZ = 1/RA + 1/RB + 1/RC其中，RA、RB、RC分别为三角形连接中的三个电阻。

三、电阻星形连接与三角形连接的等效性通过对电阻星形连接和三角形连接的等效变换公式的分析，我们可以得出结论：电阻星形连接与三角形连接是等效的。

在电路分析中，等效电路可以简化复杂的电路结构，使计算更加方便。

通过等效变换，我们可以将电阻星形连接转换为三角形连接，或将三角形连接转换为星形连接，从而简化电路的计算过程。

电阻的星型与三角形的等效变换例题在电路中，电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。

通过将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，可以简化电路分析过程，使得问题更容易解决。

在本文中，我们将深入探讨电阻的星型与三角形的等效变换，以帮助读者更好地理解这一概念。

1. 电阻的星型与三角形的等效变换概述在电路分析中，星型电阻网络由三个电阻分支组成，形状类似于星型，而三角形电阻网络由三个电阻分支组成，形状类似于三角形。

当需要对这样的电阻网络进行分析时，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，从而简化电路分析的复杂度。

2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。

通过合并相邻的电阻，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络。

这种等效变换的原理在于保持电路中的等效电阻值不变，从而简化电路分析的过程。

3. 电阻的星型与三角形的等效变换例题分析举例来说，对于一个星型电阻网络，我们可以按照以下步骤将其转换为等效的三角形电阻网络：- 合并星型电阻网络中的相邻电阻，得到等效的三角形电阻网络；- 计算等效的三角形电阻网络的总电阻值。

类似地，对于一个三角形电阻网络，我们可以按照以下步骤将其转换为等效的星型电阻网络：- 合并三角形电阻网络中的相邻电阻，得到等效的星型电阻网络；- 计算等效的星型电阻网络的总电阻值。

通过以上步骤，我们可以将星型与三角形电阻网络之间进行等效变换，从而简化电路分析的过程。

4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中，电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。

以电子电路设计为例，当需要对复杂的电路进行分析与设计时，可以利用星型与三角形的等效变换，将复杂的电路结构简化为更容易分析的形式，从而提高电路设计的效率与精度。

电阻的星形与三角形的等效变换例题电阻的星形与三角形的等效变换是电路分析中常见的问题。

通过等效变换，可以简化复杂的电路结构，使得对电路的分析和计算更加方便和高效。

在本文中，我将针对电阻的星形与三角形的等效变换例题展开讨论，从浅入深地探讨这一主题，帮助您更全面地理解电路分析中的等效变换方法。

1. 电阻的星形与三角形在电路分析中，星形与三角形是两种常见的电阻连接方式。

在星形连接中，三个电阻以一端共同连接在一起，另一端分别连接到电路的其余部分；而在三角形连接中，三个电阻以一端各自连接在一起，另一端也分别连接到电路的其余部分。

针对这种电阻连接方式，我们需要探讨如何进行等效变换，从而简化电路的分析过程。

2. 电阻的星形与三角形的等效变换我们来看一道例题：如何将一个包含星形连接的电阻网络转换为等效的三角形连接？这个问题就涉及到了电路分析中的等效变换方法。

通过分析电路结构和使用等效变换公式，我们可以将星形连接的电阻网络转化为等效的三角形连接，从而简化电路结构，使得后续的计算更加方便和直观。

这个过程需要我们对等效变换公式有深入的理解，以及对电路连接方式的分析能力。

3. 案例分析举一个具体的例子来说明：假设我们有一个包含星形连接的电阻网络，我们需要将其转化为等效的三角形连接。

我们可以根据等效变换的公式，利用电阻的数学关系和连接方式，逐步推导出等效的三角形连接电阻值。

在这个过程中，我们需要考虑电阻之间的串并联关系，以及星形与三角形连接的特点，从而正确地进行等效变换。

4. 总结与回顾通过本文的讨论，我们深入探讨了电阻的星形与三角形的等效变换例题，以及在电路分析中的重要意义。

我们从简到繁地分析了等效变换的原理和方法，帮助您更全面地理解了这一主题。

在深入讨论等效变换的过程中，我们强调了公式推导、案例分析和结论总结的重要性，以及对电路连接方式的理解和分析能力。

5. 个人观点和理解在我看来，电阻的星形与三角形的等效变换是电路分析中的重要内容，它帮助我们简化复杂的电路结构，提高分析和计算的效率。