第三篇_电阻星形连接与三角形连接的等效变换
- 格式:doc
- 大小:434.50 KB
- 文档页数:3
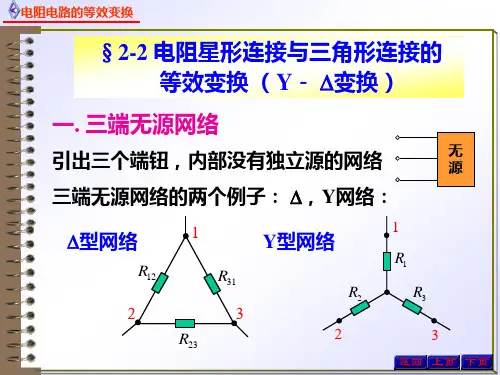
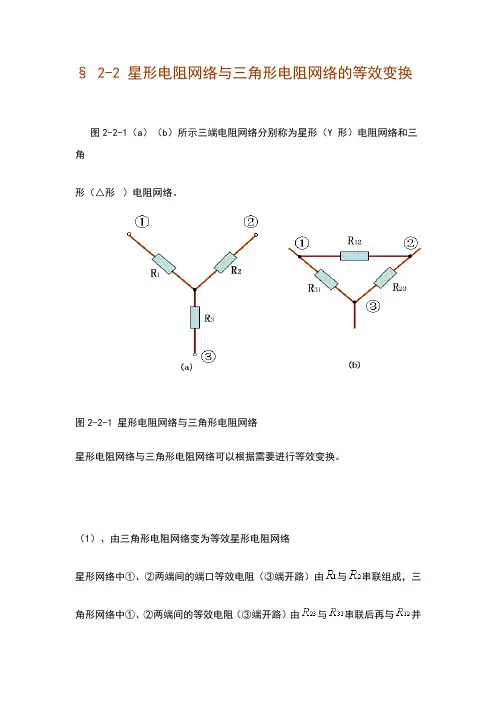
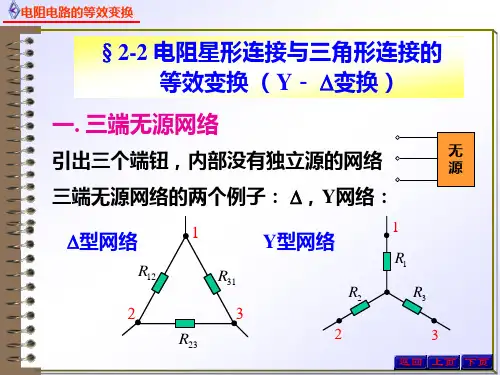
§ 2-2 星形电阻网络与三角形电阻网络的等效变换图2-2-1(a)(b)所示三端电阻网络分别称为星形(Y 形)电阻网络和三角形(△形)电阻网络。
图2-2-1 星形电阻网络与三角形电阻网络星形电阻网络与三角形电阻网络可以根据需要进行等效变换。
(1)、由三角形电阻网络变为等效星形电阻网络星形网络中①、②两端间的端口等效电阻(③端开路)由与串联组成,三角形网络中①、②两端间的等效电阻(③端开路)由与串联后再与并联组成。
令此两等效电阻相等,即得(③端开路)(2-2-1)同理(①端开路)(2-2-2)(②端开路)(2-2-3)由式(2-2-1)至(2-2-3)联立得(2-2-4)(2-2-5)(2-2-6)以上三式是由三角形电阻网络变为等效星形电阻网络时计算星形网络电阻的公式。
这三个公式的结构规律可以概括为:星形网络中的一个电阻,等于三角形网络中联接到对应端点的两邻边电阻之积除以三边电阻之和。
(2)、由星形电阻网络变为等效三角形电阻网络可将式(2-2-4)、(2-2-5)、(2-2-6)对、和联立求解得(2-2-7)(2-2-8)(2-2-9)这是由星形电阻网络变换为等效三角形电阻网络时计算三角形网络电阻的公式。
这三个公式的结构规律可以概括为:三角形网络中一边的电阻,等于星形网络中联接到两个对应端点的电阻之和再加上这两个电阻之积除以另一电阻。
(3)、对称三端网络(symmetrical three –terminal resistance network)三个电阻相等的三端网络称为对称三端网络。
对称三端电阻网络的等效变换:已知三角形网络电阻为变换为等效星形电阻网络的等效电阻为相反的变换是就是说:对称三角形电阻网络变换为等效星形电阻网络时,这个等效星形电阻网络也是对称的,其中每个电阻等于原对称三角形网络每边电阻的。
对称星形电阻网络变换为等效三角形电阻网络时,这个等效三角形电阻网络也是对称的,其中每边的电阻等于原对称星形网络每个电阻的3倍。

电阻星形连接与三角形连接的等效变换公式一、电阻星形连接的等效变换公式在电路中,星形连接是指将三个电阻分别连接在一个共节点上,形成一个星形的连接方式。
在星形连接中,我们可以通过等效变换将星形连接转换为三角形连接。
设电阻A、B、C分别为星形连接中的三个电阻,它们与共节点的连线分别为AB、AC、BC。
根据星形连接的特性,我们可以得到以下关系式:1/RA = 1/AB + 1/AC1/RB = 1/AB + 1/BC1/RC = 1/AC + 1/BC根据以上关系式,我们可以推导出电阻星形连接的等效变换公式:1/RA = 1/R1 + 1/R2 + 1/R31/RB = 1/R1 + 1/R2 + 1/R31/RC = 1/R1 + 1/R2 + 1/R3其中,R1、R2、R3分别为星形连接中的三个电阻。
二、电阻三角形连接的等效变换公式与电阻星形连接相反,电阻三角形连接是指将三个电阻分别两两相连,形成一个三角形的连接方式。
在三角形连接中,我们可以通过等效变换将三角形连接转换为星形连接。
设电阻X、Y、Z分别为三角形连接中的三个电阻,它们之间的连线分别为XY、XZ、YZ。
根据三角形连接的特性,我们可以得到以下关系式:1/RX = 1/XY + 1/XZ1/RY = 1/XY + 1/YZ1/RZ = 1/XZ + 1/YZ根据以上关系式,我们可以推导出电阻三角形连接的等效变换公式:1/RX = 1/RA + 1/RB + 1/RC1/RY = 1/RA + 1/RB + 1/RC1/RZ = 1/RA + 1/RB + 1/RC其中,RA、RB、RC分别为三角形连接中的三个电阻。
三、电阻星形连接与三角形连接的等效性通过对电阻星形连接和三角形连接的等效变换公式的分析,我们可以得出结论:电阻星形连接与三角形连接是等效的。
在电路分析中,等效电路可以简化复杂的电路结构,使计算更加方便。
通过等效变换,我们可以将电阻星形连接转换为三角形连接,或将三角形连接转换为星形连接,从而简化电路的计算过程。

电阻的星型与三角形的等效变换例题在电路中,电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。
通过将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,可以简化电路分析过程,使得问题更容易解决。
在本文中,我们将深入探讨电阻的星型与三角形的等效变换,以帮助读者更好地理解这一概念。
1. 电阻的星型与三角形的等效变换概述在电路分析中,星型电阻网络由三个电阻分支组成,形状类似于星型,而三角形电阻网络由三个电阻分支组成,形状类似于三角形。
当需要对这样的电阻网络进行分析时,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,从而简化电路分析的复杂度。
2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。
通过合并相邻的电阻,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络。
这种等效变换的原理在于保持电路中的等效电阻值不变,从而简化电路分析的过程。
3. 电阻的星型与三角形的等效变换例题分析举例来说,对于一个星型电阻网络,我们可以按照以下步骤将其转换为等效的三角形电阻网络:- 合并星型电阻网络中的相邻电阻,得到等效的三角形电阻网络;- 计算等效的三角形电阻网络的总电阻值。
类似地,对于一个三角形电阻网络,我们可以按照以下步骤将其转换为等效的星型电阻网络:- 合并三角形电阻网络中的相邻电阻,得到等效的星型电阻网络;- 计算等效的星型电阻网络的总电阻值。
通过以上步骤,我们可以将星型与三角形电阻网络之间进行等效变换,从而简化电路分析的过程。
4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中,电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。
以电子电路设计为例,当需要对复杂的电路进行分析与设计时,可以利用星型与三角形的等效变换,将复杂的电路结构简化为更容易分析的形式,从而提高电路设计的效率与精度。

公正处法人授权委托书范本一、前言为了明确公正处法人的授权范围和内容,确保代理人能够合法、合规地代表法人行事,特制定本授权委托书。
本授权委托书旨在规范法人授权行为,保障法人及其代理人的合法权益,维护社会经济秩序。
二、授权主体1. 授权单位:×××公正处2. 法定代表人:×××3. 授权人:×××三、授权范围1. 代理人代表公正处参加各类法律诉讼活动,包括但不限于起诉、应诉、举证、质证、调解、和解等。
2. 代理人代表公正处与各类当事人进行法律事务谈判、协商,并签署相关法律文件。
3. 代理人代表公正处处理各类法律事务,包括但不限于合同审查、起草、签订、变更、解除等。
4. 代理人代表公正处参加各类行政复议、行政诉讼活动,维护公正处的合法权益。
5. 代理人代表公正处处理各类法律咨询、法律培训、法律宣传等活动。
6. 代理人代表公正处与各类政府部门、企事业单位、社会团体等进行法律事务往来。
7. 代理人代表公正处处理其他各类法律事务,包括但不限于知识产权、劳动关系、交通事故等。
四、授权期限本授权委托书的有效期为自授权人之签名或盖章之日起至法定代表人书面声明本授权作废之日止。
五、授权方式1. 法定代表人签字或盖章。
2. 公正处盖章。
六、注意事项1. 代理人应当在授权范围内行事,不得超出授权范围进行任何活动。
2. 代理人不得转委托授权,不得将授权事项转让给他人。
3. 代理人不得以公正处名义从事任何非法活动,不得损害公正处的合法权益。
4. 代理人应当严格遵守国家法律法规,合规行事。
5. 代理人应当保持与当事人的良好沟通,确保授权事项的顺利进行。
6. 代理人应当及时向法定代表人报告授权事项的进展情况。
七、法律后果1. 代理人依据本授权委托书行事,其法律后果由公正处承担。
2. 代理人超出授权范围行事,其法律后果由代理人自行承担。
3. 代理人违反国家法律法规、本授权委托书约定,给公正处造成损失的,应当承担赔偿责任。


三角形和星形电阻电路的等效变换三角形和星形电阻电路的等效变换,这个话题听起来好像有点高深莫测,但其实它就像是我们日常生活中的一道数学题目。
今天,我就来给大家讲讲这道题目的答案,希望能够帮助大家更好地理解这个概念。
我们来看看三角形电阻电路。
三角形电阻电路是指由三个电阻器组成的电路,这三个电阻器的阻值可以不同。
当我们把这三个电阻器连接在一起时,就会形成一个三角形。
那么,这个三角形电阻电路有什么特点呢?三角形电阻电路的特点就是它的电流分布是均匀的。
这是因为在三角形中,每个顶点都是一个交点,而根据欧姆定律,电流通过交点时会受到阻碍。
所以,当三个电阻器的阻值不它们所承受的电流也会不同。
但是,由于三角形的结构特点,这些电流会被平均分配到每个顶点上,从而使得整个电路的电流分布变得均匀起来。
接下来,我们再来看看星形电阻电路。
星形电阻电路是指由一个电阻器和一个电源组成的电路,这个电阻器的阻值很小,可以忽略不计。
那么,这个星形电阻电路有什么特点呢?星形电阻电路的特点就是它的电流只从正极流向负极。
这是因为在星形结构中,电源的一端连接着一个很小的电阻器,而另一端则直接连接到了负载上。
由于这个小电阻器的阻值很小,所以它对整个电路的影响可以忽略不计。
因此,在星形结构中,电流只会沿着一个方向流动,即从正极流向负极。
那么,如何将这两个电路进行等效变换呢?其实很简单,只需要把三角形电阻电路中的三个电阻器分别替换成一个星形电阻器和两个相同的较小电阻器就可以了。
这样一来,原来的三角形电阻电路就变成了一个由一个星形电阻器和两个相同的较小电阻器组成的新的电路。
这个新的电路的特点是什么呢?这个新的电路的特点就是它的电流分布仍然是均匀的。
这是因为在这个新的电路中,虽然只有一个星形电阻器和两个相同的较小电阻器组成了负载部分,但是由于这两个较小的电阻器的阻值相同且很小,所以它们对整个负载的影响也可以忽略不计。
因此,在整个负载部分中仍然存在着类似于三角形电阻电路中的均匀电流分布情况。

三角形和星形电阻电路的等效变换亲爱的朋友们,今天我们来聊聊一个非常有趣的话题——三角形和星形电阻电路的等效变换。
你们知道吗?这个话题可是涉及到我们日常生活中用电的问题哦!那么,让我们一起来揭开这个谜底吧!我们来说说三角形电阻电路。
三角形电阻电路是由三个电阻组成的一个线性电路,它的特点是三个电阻的阻值不同,但总阻值为其中最小的那个电阻值。
三角形电阻电路在实际应用中非常常见,比如我们家里的电视机、空调等等,都有可能使用到三角形电阻电路。
那么,三角形电阻电路有什么特点呢?我们来慢慢道来。
三角形电阻电路的特点之一就是它的等效电阻。
你们知道等效电阻是什么吗?等效电阻就是把一个复杂的电路简化成一个简单的电路,而这个简单的电路的阻值与原来的复杂电路的阻值相同。
那么,三角形电阻电路的等效电阻怎么求呢?别着急,我们马上就告诉你答案。
三角形电阻电路的等效电阻可以通过以下方法求得:我们需要找到三角形电阻电路中的两个并联电阻,然后用这两个并联电阻的阻值除以它们的乘积,就可以得到三角形电阻电路的等效电阻了。
是不是很简单呢?接下来,我们再来说说星形电阻电路。
星形电阻电路是由一个中心点和四个电阻组成的一个非线性电路,它的特点是四个电阻的阻值相等,但中心点的阻值不等于四个电阻的阻值之和。
星形电阻电路在实际应用中也非常常见,比如我们家里的收音机、音响等等,都有可能使用到星形电阻电路。
那么,星形电阻电路有什么特点呢?我们接着来聊聊。
星形电阻电路的特点之一就是它的等效电阻。
你们知道等效电阻是什么吗?等效电阻就是把一个复杂的电路简化成一个简单的电路,而这个简单的电路的阻值与原来的复杂电路的阻值相同。
那么,星形电阻电路的等效电阻怎么求呢?别着急,我们马上就告诉你答案。
星形电阻电路的等效电阻可以通过以下方法求得:我们需要找到星形电阻电路中的中心点和四个并联电阻,然后用中心点的阻值除以四个并联电阻的阻值之和,就可以得到星形电阻电路的等效电阻了。
三角形和星形电阻电路的等效变换1. 引言大家好,今天我们聊聊电路中的那些事,特别是三角形和星形电阻电路的等效变换。
听起来是不是有点高大上?其实嘛,这就是把电阻放在不同的位置,让它们的工作变得更轻松而已。
电阻就像是电路里的小助手,有时候换个地方就能发挥出意想不到的效果,就像你换个角度看问题,顿时豁然开朗。
我们在这儿就像是在煮面,偶尔换点调料,味道也会大变样呢!2. 三角形电阻电路2.1 三角形电阻的特征首先,我们得认识一下三角形电阻。
想象一下,电阻排成一个三角形,三个边各自相连,就像三兄弟一起打拼。
这种连接方式让电流在不同的电阻之间穿梭,仿佛是在玩“你追我赶”的游戏。
而且,三角形的结构让我们能轻松计算出每个电阻的作用,真是聪明的设计!2.2 三角形电阻的用途那么,三角形电阻到底有什么用呢?比如,当我们需要调节电流或电压时,三角形电阻就派上了用场。
它能够将复杂的电路简化,让我们一目了然。
这就像是把一锅杂烩理顺成一碗清汤,简单明了,心里也舒服。
可是呢,三角形电阻有时候会让电流走得比较复杂,不容易理解。
3. 星形电阻电路3.1 星形电阻的特征说完了三角形,我们再来说说星形电阻。
这个星形可不是什么美丽的星空,而是电阻像星星一样,中心有个共同的节点,其他的电阻都从这个节点出发。
这就好比我们一家人围坐在一起,大家都有自己的事,但又紧紧联系在一起。
星形电阻的连接方式让电流分流更均匀,效率高得多,真是聪明绝顶!3.2 星形电阻的优势星形电阻的优势就在于它能有效降低电路的复杂度,简化计算。
想象一下,原本你得对着一大堆复杂的数学公式挠头,现在只需几笔,就能轻松搞定。
这样的电路就像是我们日常生活中的简约风格,虽然简单,却能达到很好的效果。
再说,星形电阻也能避免过大的电流,保护其他部件,就像是家里有个“大哥”,照顾着其他小弟弟们。
4. 三角形与星形的等效变换4.1 等效变换的原理好啦,说到这儿,咱们得聊聊怎么把三角形电阻变成星形电阻。
第三篇电阻星形连接与三角形连接的等效变
换
-CAL-FENGHAI.-(YICAI)-Company One1
第三篇电阻星形连接与三角形连接的等效变换
图 1 一 1 ( a )所示是一个桥式电路,显然用电阻串并联简化的办法求得端口 ab 处的等效电阻是极其困难的。
如果能将连接在 1 、 2 、 3 、三个端子间的 R12R23R31构成的三角形连接电路,等效变换为图 1 一 1 ( b )所示的由
R1R2R3构成的星形连接电路,则可方便地应用电阻串并联简化的办法求得端口ab 处的等效电阻,这就是工程实际中经常遇到的星形、三角形等效变换问题(简称 Y ―△变换)。
图1
在这里叙述 Y ―△变换并非要求同学们掌握此变换,而是通过讲解,了解变换的过程意义,为课程后续内容的学习(三相电路)先行建立一个感性认识,从而为更进一步的学习奠定基础。
等效要解决的问题是:图 1 一 2 ( a )所示三角形连接(连接)与图 1 一 2 ( b )星形连接( Y 连接),就其 1、 2 、 3 三个端子而言,要求对外等效。
要完成等效,应明确R1R2R3三个 Y 连接电阻与R12R23R31三个连接电阻应满足什麽关系。
一种推导等效变换的办法是两电路在一个对应端子悬空的同等条件下,分别测两电路剩余两端子间的电阻,并要求测得的电阻相等。
式 l 可方便地用来求三角形连接电阻等效的星形连接电阻。
若由星形连接求等效三角形连接的公式可将式!变换一下,即可得到。
电阻的星形和三角形连接的等效变换1、电阻的星形和三角形连接三个电阻元件首尾相连接,连成一个封闭的三角形,三角形的三个顶点接到外部电路的三个节点,称为电阻元件的三角形连接简称△连接,如图 2.7(a )所示。
三个电阻元件的一端连接在一起,另一端分别连接到外部电路的三个节点,称为电阻元件的星形连接,简称Y 形连接,如图2.7(b )所示。
三角形连接和星形连接都是通过三个节点与外部电路相连,它们之间的等效变换是要求它们的外部特性相同,也就是当它们的对应节点间有相同的电压12U 、23U 、31U 时,从外电路流入对应节点的电流1I 、2I 、3I 也必须分别相等,即Y-△变换的等效条件。
一种简单的推导等效变换方法是:在一个对应端钮悬空的同等条件下,分别计算出其余两端钮间的电阻,要求计算出的电阻相等。
悬空端钮3时,可得:12233112122331()R R R R R R R R ++=++ 悬空端钮2时,可得:31122331122331()R R R R R R R R ++=++ 悬空端钮1时,可得:23123123122331()R R R R R R R R ++=++联立以上三式可得:123111223311223212233131233122331R R R R R R R R R R R R R R R R R R =++=++=++ (2-2) 式(2-2)是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。
从式(2-2)可解的:121212323232313131312R R R R R R R R R R R R R R R R R R =++=++=++ (2-3)以上互换公式可归纳为:=Y ∆∆形相邻电阻的乘积形电阻形电阻之和=Y ∆形电阻两两乘积之和形电阻Y 形不相邻电阻 当Y 形连接的三个电阻相等时,即123Y R R R R ===,则等效△形连接的三个电阻也相等,它们等于1223313Y R R R R R ∆==== 或 1=3Y R R ∆ (2-4)。
第三篇电阻星形连接与三角形连接的等效变换
图 1 一 1 ( a )所示是一个桥式电路,显然用电阻串并联简化的办法求得端口ab 处的等效电阻是极其困难的。
如果能将连接在 1 、 2 、 3 、三个端子间的R12R23R31构成的三角形连接电路,等效变换为图 1 一 1 ( b )所示的由R1R2R3构成的星形连接电路,则可方便地应用电阻串并联简化的办法求得端口ab 处的等效电阻,这就是工程实际中经常遇到的星形、三角形等效变换问题(简称Y ―△变换)。
图1
在这里叙述Y ―△变换并非要求同学们掌握此变换,而是通过讲解,了解变换的过程意义,为课程后续内容的学习(三相电路)先行建立一个感性认识,从而为更进一步的学习奠定基础。
等效要解决的问题是:图 1 一 2 ( a )所示三角形连接(连接)与图1 一2 ( b )星形连接(Y 连接),就其1、2 、3 三个端子而言,要求对外等效。
要完成等效,应明确R1R2R3三个Y 连接电阻与R12R23R31三个连接电阻应满足什麽关系。
一种推导等效变换的办法是两电路在一个对应端子悬空的同等条件下,分别测两电路剩余两端子间的电阻,并要求测得的电阻相等。
式l 可方便地用来求三角形连接电阻等效的星形连接电阻。
若由星形连接求等效三角形连接的公式可将式!变换一下,即可得到。