电阻的星形联结与三角形联结

星型连接和三角形连接的相电压和线电压的关系
星形连接是线电压是相电压的根号3倍,而三角形连接是相电压是等于线电压的。

每相负载中流过的电流为相电流，流过每条电源线中的电流为线电流。

线电流与相电流的关系也与三相负载的接法有关。

当三相负载为三角形联结时，每一线电流都分成两路，其中一路为一相，另一路由两相串联组成，所以线电流要大于相电流，即线电流是相电流的√3倍；当三相负载为星形联结时，线电流和相电流相等。

三相电路特点：
对称三相电源和对称三相负载相连接，称为对称三相电路（一般情况下，电源总是对称的）。

三相电源与负载之间的连接方式有y-y,△-y,△-△,y-△连接方式。

三相电路实际是正弦交流电路的一种特殊类型。

在三相电路中，三相功率的相连接方式同意于功率每相的额定电压和电源的线电压。

由于等距三相电路中每组的积极响应都就是与鞭策同相序的对秤。

所以，每二者不但接法有效值成正比，相电流有效值也成正比。

而且每接法与电流的相位差也成正比。

从而每相的军功功率成正比。

复杂电路中的电阻计算口诀1、口诀复杂电路变简单，可将星角来变换。

变时一点要牢记，外接三点不能变。

星变角时求某边，两两积和除对面。

角变星时求某枝，两臂之积除和三。

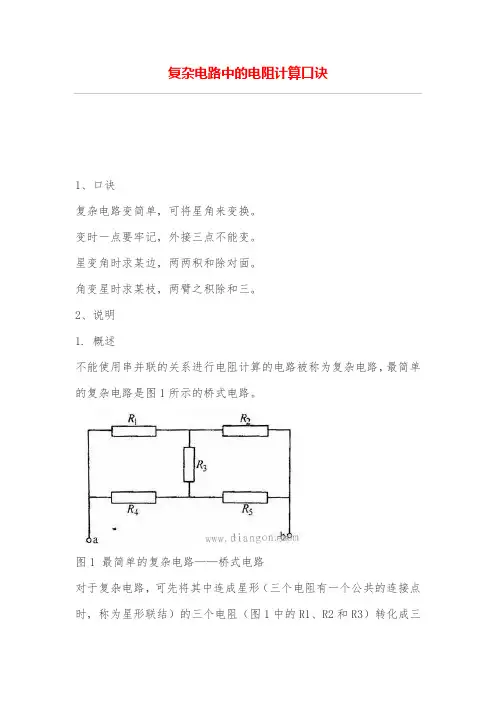
2、说明1. 概述不能使用串并联的关系进行电阻计算的电路被称为复杂电路，最简单的复杂电路是图1所示的桥式电路。

图1 最简单的复杂电路——桥式电路对于复杂电路，可先将其中连成星形（三个电阻有一个公共的连接点时，称为星形联结）的三个电阻（图1中的R1、R2和R3）转化成三角形电路（三个电阻依次连接成为一个闭合回路时，称为三角形联结），或将其中连成三角形的三个电阻（图1中的R1、R3和R4）转化成星形电路，这就是所谓的电阻星-三角变换问题。

进行上述变换后，原有的复杂电路就会转变为简单电路，就可以用串并联的计算方法求出总电阻值。

电阻星-三角变换的理论推导相对较复杂，在此不准备给出。

下面只给出转换方法口诀和使用方法举例。

2. 口诀说明设星形联结的三个电阻分别是R1、R2和R3，三角形联结的三个电阻分别是R12（对应星形连接的R1和R2）、R23（对应星形连接的R2和R3）和R31（对应星形连接的R3和R1），参照图2说明转换口诀的使用方法。

图2 电阻的星-三角变换电路（1）当由星形联结转换成三角形联结时，口诀为“星变角时求某边，两两积和除对面”。

这里的“两两”是指星形联结时的每两个电阻，“两两积和”即为（R1R2+ R2R3+ R3R1）；“对面”是指与转换成三角形联结后的一个电阻相对的原星形联结的那个电阻，如图2中R12的“对面”应是R3。

由此可得到由星形联结转换成三角形联结时的三个电阻计算公式为R12＝（R1R2+ R2R3+ R3R1）/R3R23＝（R1R2+ R2R3+ R3R1）/R1R31＝（R1R2+ R2R3+ R3R1）/R2（2）当由三角形联结转换成星形联结时，口诀为“角变星时求某枝，两臂之积除和三”。

这里的“两臂”是指与转换成星形联结的一个电阻（后面称为“一枝”，例如R1）同一个顶点的三角形联结时的两个电阻（例如对应R1的两臂是R12和R31），“和三”即为三角形联结时三个电阻之和，即（R12+ R23+ R31）。

电磁学论文班级：13物理（1）班姓名：李建民学号：20131040212复杂电路的计算天水师范学院，13物理（1）班，李建民摘要解决复杂电路计算的基本公式是基尔霍夫方程组，原则上它可以用来计算任何复杂电路中每一支电路中的电流，可是实际的电路计算常常并不需要计算每一支电路的电流，而只计算某一支路的电流，或某部分电路的等效电阻等。

在解决这样的问题中，可运用基尔霍夫方程组导出的定理，可以简化计算。

这些定理有等效电源定理、叠加定理、Y—△等效代换定理。

关键词复杂电路基尔霍夫方程组等效电源定理、叠加定理、Y—△等效代换定理一、定理的表述在此部分，我将所要引用的几个定理作以详细表述。

（一）基尔霍夫方程组。

1、基尔霍夫第一方程组。

基尔霍夫第一方程组又称节点电流方程组，它的理论基础是恒定条件。

我们规定：流向节点的电流前写负号，反之，流出节点的电流前写正号，则此节点处的代数和为0。

.0321=+--I I I2、 基尔霍夫第二方程组。

基尔霍夫第二方程组又称回路电压方程组，它的理论基础是恒定电场的环路定理。

我们规定：在一个回路中预先确定一绕行方向，电势从高到低降落为正，从低到高降落为负，则沿回路环绕一周，电势降落代数和为0。

即：.0)(14323222111=-+++++-R I R r I R I r I εε（二） 电压源与电流源 等效电源定理。

1、电压源与电流源。

一个实际电源可以看成是电动势为ε内阻为0的理想电压源与内阻r 的串联。

当电源两端接上外电阻R 时，其上就有电流和电压。

在理想情况下，r=0，不管外电阻如何，电源提供的电压总是恒定值ε，我们把这种电源叫恒压源（即理想电压源）。

在非理想情况下，0≠r ，这样的电源叫电压源，它相当于内阻r 与恒压电源串联，如图a我们也可以设想有一种理想电源，不管外电阻如何变化，它总是提供不变的电流0I ，0I 相当于恒压源中的电动势。

这种理想的电源叫做恒流源。

一个电池串联很大的电阻，就近似于一个恒流源，因为它对外电阻所提供的电流基本上由电动势和所串联的大电阻决定，几乎于外电阻无关。

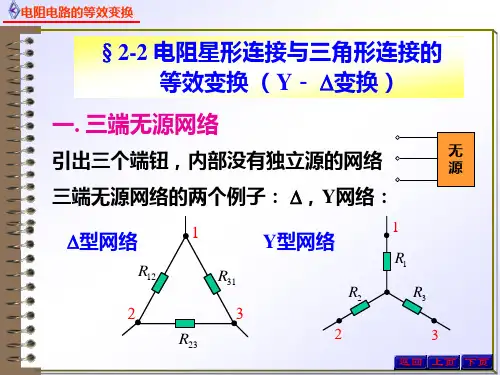
电阻星形连接与三角形连接的等效变换公式一、电阻星形连接的等效变换公式在电路中，星形连接是指将三个电阻分别连接在一个共节点上，形成一个星形的连接方式。

在星形连接中，我们可以通过等效变换将星形连接转换为三角形连接。

设电阻A、B、C分别为星形连接中的三个电阻，它们与共节点的连线分别为AB、AC、BC。

根据星形连接的特性，我们可以得到以下关系式：1/RA = 1/AB + 1/AC1/RB = 1/AB + 1/BC1/RC = 1/AC + 1/BC根据以上关系式，我们可以推导出电阻星形连接的等效变换公式：1/RA = 1/R1 + 1/R2 + 1/R31/RB = 1/R1 + 1/R2 + 1/R31/RC = 1/R1 + 1/R2 + 1/R3其中，R1、R2、R3分别为星形连接中的三个电阻。

二、电阻三角形连接的等效变换公式与电阻星形连接相反，电阻三角形连接是指将三个电阻分别两两相连，形成一个三角形的连接方式。

在三角形连接中，我们可以通过等效变换将三角形连接转换为星形连接。

设电阻X、Y、Z分别为三角形连接中的三个电阻，它们之间的连线分别为XY、XZ、YZ。

根据三角形连接的特性，我们可以得到以下关系式：1/RX = 1/XY + 1/XZ1/RY = 1/XY + 1/YZ1/RZ = 1/XZ + 1/YZ根据以上关系式，我们可以推导出电阻三角形连接的等效变换公式：1/RX = 1/RA + 1/RB + 1/RC1/RY = 1/RA + 1/RB + 1/RC1/RZ = 1/RA + 1/RB + 1/RC其中，RA、RB、RC分别为三角形连接中的三个电阻。

三、电阻星形连接与三角形连接的等效性通过对电阻星形连接和三角形连接的等效变换公式的分析，我们可以得出结论：电阻星形连接与三角形连接是等效的。

在电路分析中，等效电路可以简化复杂的电路结构，使计算更加方便。

通过等效变换，我们可以将电阻星形连接转换为三角形连接，或将三角形连接转换为星形连接，从而简化电路的计算过程。

第五讲 电阻电路的串、并联等效变换和星形—三角形等效变换 电压源与电流源的等效变换；时间：2学时重点和难点：无源电路的等效化简。

目的：让学生掌握电阻的连接方式及等效计算、变换；掌握电源的等效变换方法和无源电路的等效化简。

教学方法：多媒体演示、课堂讲授主要教学内容：一、电阻的串、并联等效变换1、电阻的串联：1）串联等效电阻图示为n 个电阻的串联等效电路，其特点是电路没有分支，通过各电阻的电流相同。

根据KVL 和欧姆定律有 n u u u u +++= 21i R i R i R n +++= 21()i R R R n ++=21Ri =其中 ：∑==+++==n k k n R R R R i u R 121 R 称为n 个串联电阻的等效电阻。

可见，串联电阻的等效电阻等于各个串联电阻之和，其等效条件是在同一电压作用下电流保持不变。

图a ）、（b ）两个电路的内部结构虽然不同，但是，它们在a 、b 端钮处的u 、i 关系却完全相同，即它们在端钮处对外显示的伏安特性是相同的，所以称图（b ）为图（a ）的等效电路，这种替代称为等效变换。

2）串联电路分压公式在电阻串联电路中，各电阻上的电压为u RR i R u k k k == 可见，电路中各个串联电阻的电压与电阻值成正比，上式称为串联电路分压公式。

3）串联电路功率222221Ri i R i R i R ui p n =+++==上式表明，n 个电阻串联吸收的总功率，等于各个电阻吸收的功率之和，等于等效电阻吸收的功率。

2、电阻的并联1）并联等效电阻图所示电路为n 个电阻的并联电路，其特点是各并联电阻两端具有相同的电压，即互相并联的各电阻接在同一对节点之间。

根据KCL 和欧姆定律有n i i i i +++= 21u G u G u G n +++= 21u G G G n )(21+++=Gu =其中 ：∑==+++==n k k n G G G G u i G 121 或写成： ∑==+++=n k kn R R R R R 12111111 上式称为n 个并联电阻的等效电导，其倒数为等效电阻。

电阻星形联结与三角形联结的等效变换下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!电阻星形联结与三角形联结的等效变换在电路理论中，电阻的星形联结和三角形联结是常见的电路连接方式。

三相电的三角形接法与星形接法三相电的三角形接法：三相电的三角形接法是将各相电源或负载依次首尾相连，并将每个相连的点引出，作为三相电的三个相线。

三角形接法没有中性点，也不可引出中性线，因此只有三相三线制。

添加地线后，成为三相四线制。

三角形接法的三相电，线电压等于相电压而线电流等于相电流的√3倍。

三相电的星形接法是将三相电源绕组或负载的一端都接在一起构成中性线，由于均衡的三相电的中性线中电流为零，故也叫零线：三相电源绕组或负载的另一端的引出线，分别为三相电的三个相线。

远程输电时，只使用三根相线，形成三相三线制。

到达用户的电路，往往涉及220V和380V两种电压，需三根相线和一根零线，形成三相四线制。

用户为避免漏电形成的触电事故，还要添加一根地线，这时就有三根相线，一根零线和一根地线，故也有三相五线制的说法。

常用的接法对称三相四线Y－Y系统是常见常用的系统，有三条火线、一条中线。

星形接法的三相电，线电压是相电压的根号3倍，而线电流等于相电流。

当三相负载平衡时，即使连接中性线，其上也没有电流流过。

三相负载不平衡时，应当连接中性线，否则各相负载将分压不等。

星形接法主要应用在高压大型或中型容量的电动机中，定子绕组只引出三根线。

对于星形接法，各相负载平衡，则任何时刻流经三相的电流矢量和等于零。

星形(Y)接法和三角形(△)接法关系密切，其负载相电压、相电流与对称三相线电压、线电流关系如下：星形接法：I线=I相，U线=√3×U相，P相=U相×I相，P=3P相=1/√3×U线×I相=1/√3×U线×I线；三角接法：I线=√3×I相，U线=U相，P相=I相×U相，P=3P相=√3×I线×U相=√3×I线×U线。

说明：三角(△)联接，Iab=Ia向量+Ib向量=(Ia+Ib)×cos30°=2Ia×√3/2=√3×Ia，线电流是相电流的根号三倍。

第一章电路基本概念和电路定律2.已知空间有a、b两点，电压Uab=10V，a点电位为φa=4V，则b点电位φb为（）。

A.6VB.-6VC.14VD.10V3.当电路中电流的参考方向与电流的真实方向相反时，该电流（）。

A.一定为正值B.一定为负值C.不肯定是正值或负值D.有时为正值，有时为负值4.当电阻R上u、i的参考方向为非关联时，欧姆定律的表达式应为（）。

A.u=RiB. u=-RiC. u=R ▏i ▏D. u=-Gi5.某一电阻R上的u、i的参考方向非关联，令u=-10V,消耗功率为0.5W，则电阻R为（）。

A.200ΩB. -200ΩC. ±200ΩD. ±100Ω13.有一2V电压源，内电阻为0.1Ω，当外电路断路时，电路中的电流和端电压分别为（）。

A.0A,2VB.20A,0VC.2A,0VD.0A,0V14.下列理想元件在电路中总是消耗功率的是（）A.电源B.电感C.电阻D.电容15.当元件两端电压与通过元件的电流取关联参考方向时，且通过计算其电压、电流都为正，即该元件（）功率。

A.吸收B.发出C.不能确定D.有时吸收，有时发出19.电源置零，即将电压源▁▁▁▁，电流源▁▁▁▁。

下列叙述正确的是（）。

A.开路，短路B.短路，开路C.短路，短路D.开路，开路20.运算放大器理想化的条件为输入电阻Rin=▁▁▁▁,输出电阻Ro=▁▁▁▁，放大倍数A=▁▁▁▁。

下列叙述正确的是（）。

A.∞，0，∞B.0，∞，∞C.0，0，∞D.∞，0,021. 已知在非关联参考方向下，某个元件的端电压为5V，流过该元件的电流为2mA,则该元件功率状态为（）。

A.吸收10WB.发出10WC.吸收10mWD.发出10mW22.已知某元件在关联参考方向下，吸收的功率为10kW。

如果该元件的端电压为1k V,则流过该元件的电流为（）。

A.-10AB.10AC.-10 mAD.10 mA23. 已知在关联参考方向下，某个元件的端电压为2V，流过该元件的电流为5mA,则该元件功率状态为（）。