电阻的星形和三角形连接的等效变换
- 格式:doc
- 大小:81.50 KB
- 文档页数:3

电阻三角形和星形变换公式
电阻三角形和星形变换公式是在电路中常用的一种计算方法,特别是在进行串联和并联电路计算时,可以大大简化计算的复杂度。
电阻三角形和星形变换公式是根据电路的基本原理推导出来的,通过将电路进行转换可以得到等效的电路形式,从而简化计算。
电阻三角形变换公式是指将三个电阻串联的电路转换为三个电阻并联的等效电路的方法。
具体的转换方法是:将三个电阻分别连接成一个三角形,然后将三角形中的任意一个角连接到电路的两端,从而形成一个并联电路。
这样得到的等效电路中,三个电阻的并联等效电阻就是原始电路中三个电阻的串联等效电阻。
星形变换公式是指将三个电阻并联的电路转换为三个电阻串联的等效电路的方法。
具体的转换方法是:将三个电阻分别连接成一个星形,然后将星形的中心点连接到电路的两端,从而形成一个串联电路。
这样得到的等效电路中,三个电阻的串联等效电阻就是原始电路中三个电阻的并联等效电阻。
这两种变换公式在电路的设计和分析中都有着广泛的应用,可以帮助工程师们更加高效地进行电路设计和计算。
在实际应用中,需要根据电路特点选择合适的变换公式,从而得到更加准确和简化的计算结果。
- 1 -。

电阻网络中的三角形星形等效变换解析实例电阻网络中的三角形-星形等效变换解析实例在电路分析中,等效变换是一种将复杂电路简化成简单电路的方法。
其中,三角形-星形等效变换是常用的一种方法,可以将电阻网络中的三角形形式转换为星形形式,使得电路的计算更加简便。
本文将通过几个实例来解析电阻网络中的三角形-星形等效变换,以展示这一方法的应用。
实例一:在如下电阻网络中,我们希望将三角形形式转换为星形形式:R1 R2 R3o--------o-----------o-----------o| | |RL R5 R6| | |o--------o-----------o-----------oR4 R7 R8首先,我们按照以下步骤进行等效变换:1. 将RL与R1进行并联,得到RL1;2. 将RL1与R7进行并联,得到RL2;3. 将R4与RL2进行并联,得到RL3;4. 将R5与RL3进行并联,得到RL4。
经过以上等效变换后,得到如下的星形形式电路:RL4 RL3 RL2o--------o-----------o-----------o| | |R2 R3 R8| | |o--------o-----------o-----------oR1 R5 R6通过以上变换,我们成功将电阻网络转换为了星形形式,从而简化了电路的计算。
实例二:现在考虑一个稍为复杂的电阻网络,其中包含多个三角形形式的电阻网络。
我们希望将整个电路转换为星形形式。
R2 R3o--------o----------------------o|R1 L|o|RL R4 RL|R5 L|o|R6 R7o ----------------------o----------------o为实现等效变换,我们按照以下步骤进行处理:1. 将RL与R1进行并联,得到RL1;2. 将RL1与R4进行并联,得到RL2;3. 将RL2与R5进行并联,得到RL3;4. 将R6与RL3进行并联,得到RL4;5. 将RL4与R3进行并联,得到RL5;6. 将RL5与R7进行并联,得到RL6。



电阻连接的等效变换公式电阻是电路中常见的元件之一,它可以对电流的流动产生阻碍作用。
在实际的电路中,我们经常需要对电阻进行等效变换,以便更好地分析和设计电路。
本文将介绍电阻连接的等效变换公式,帮助读者更好地理解和运用这些公式。
1. 串联电阻的等效电阻当多个电阻依次连接在一起,形成串联电路时,它们的等效电阻可以通过简单相加得到。
假设有两个电阻R1和R2串联连接在一起,它们的等效电阻可以表示为:Req = R1 + R2如果有更多的电阻串联连接在一起,可以依次相加得到总的等效电阻。
2. 并联电阻的等效电阻当多个电阻同时连接在电路中,形成并联电路时,它们的等效电阻可以通过倒数相加后再取倒数得到。
假设有两个电阻R1和R2并联连接在一起,它们的等效电阻可以表示为:1/Req = 1/R1 + 1/R2如果有更多的电阻并联连接在一起,可以依次倒数相加后再取倒数得到总的等效电阻。
3. 三角形电阻网络的等效电阻在一些特殊情况下,电路中的电阻可以组成一个三角形网络。
对于三角形电阻网络,我们可以通过等效变换将其转化为星形电阻网络,以便更好地分析和设计电路。
三角形电阻网络的等效电阻可以通过下式得到:Req = R1 * R2 / (R1 + R2 + R3)其中,R1、R2和R3分别表示三角形电阻网络中的三个电阻。
4. 星形电阻网络的等效电阻与三角形电阻网络相对应的是星形电阻网络。
对于星形电阻网络,我们可以通过等效变换将其转化为三角形电阻网络。
星形电阻网络的等效电阻可以通过下式得到:1/Req = 1/R1 + 1/R2 + 1/R3其中,R1、R2和R3分别表示星形电阻网络中的三个电阻。
5. 电阻的温度系数电阻的阻值是随温度的变化而变化的,这是由于电阻材料的特性所决定的。
电阻的温度系数是描述电阻阻值随温度变化的程度的指标,通常用符号α表示。
电阻的阻值与温度的关系可以用下式表示:Rt = R0 * (1 + α * (T - T0))其中,Rt表示温度为T时的电阻阻值,R0表示参考温度T0时的电阻阻值,α表示电阻的温度系数。

星三角电阻转换公式
星三角电阻转换公式是指将三个电阻呈三角形连接的电路转换成呈星型连接的电路时,所需使用的公式。
这个公式可以表示为:RAB = (RA*RB+ RB*RC +RC*RA)/(RC)
其中,RAB是星型电路中A和B之间的等效电阻,RA、RB和RC分别是三角形电路中三个电阻的阻值。
这个公式可以用来计算星型电阻和三角形电阻之间的等效电阻,这样就可以将一种电路拓扑结构转换成另一种,以方便电路设计和分析。
此外,星型电阻和三角形电阻的等效电阻还可以通过其他方法来计算,例如使用矩阵方法或毕奥定理等。
这些方法都可以为工程师和设计师提供准确的电路计算结果。

电阻网络中的星形三角形变换分析在电阻网络中,星形和三角形连接是常见的连接方式。
这两种连接方式在电路分析和设计中具有重要的作用。
本文将对电阻网络中的星形三角形变换进行详细分析,以帮助读者更好地理解和应用这一概念。
一、星形连接和三角形连接简介1. 星形连接在电路中,星形连接是指将三个或更多的电阻连接在一起,其中一个节点连接到电源正极,其余节点连接到电源负极。
这种连接方式常用于电路中需要提供共地或共点的情况。
2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。
三角形连接常用于电路中需要提供平衡电路或无共地的情况。
二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。
通过执行星形三角形变换,可以简化电路的分析和计算。
具体变换原理如下:1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。
设星形连接的电阻为R1,R2,R3,其中节点A连接到电源正极,节点B和C连接到电源负极。
则等效的三角形连接电阻可表示为:RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。
设三角形连接的电阻为RT,RA,RB,其中节点A、B、C两两相连,形成闭合的三角形。
则等效的星形连接电阻可表示为:R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用,其中包括但不限于以下几个方面:1. 简化电路分析和计算通过执行星形三角形变换,可以将复杂的电路转换为等效的简化电路,从而简化电路的分析和计算。
这种方法尤其适用于涉及大量电阻和复杂连接的电路。

电阻的星形与三角形的等效变换
电阻的星形与三角形的等效变换是指将电阻的星型连接电路转化为等效的三角形连接电路,或将三角形连接电路转化为等效的星型连接电路。
具体变换方法如下:
1. 电阻星型转换为等效的电阻三角形:
- 当星型电路中的三个电阻分别为R1、R2、R3时,先计算等效电阻Re:
Re = R1+R2+R3
- 然后计算等效三角形电路中的三个电阻Ra、Rb、Rc:
Ra = [(R2*R3)/(R1+R2+R3)]
Rb = [(R1*R3)/(R1+R2+R3)]
Rc = [(R1*R2)/(R1+R2+R3)]
- 得到等效的电阻三角形连接电路。
2. 电阻三角形转换为等效的电阻星型:
- 当三角形电路中的三个电阻分别为Ra、Rb、Rc时,先计算等效电阻Re:
Re = [Ra*Rb + Rb*Rc + Rc*Ra] / (Ra+Rb+Rc)
- 然后计算等效星型电路中的三个电阻R1、R2、R3:
R1 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
R2 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
R3 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
- 得到等效的电阻星型连接电路。
通过等效变换,可以简化电路分析和计算,从而更方便地求解电路中的电流、电压等参数。
电阻的星型与三角形的等效变换例题在电路中,电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。
通过将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,可以简化电路分析过程,使得问题更容易解决。
在本文中,我们将深入探讨电阻的星型与三角形的等效变换,以帮助读者更好地理解这一概念。
1. 电阻的星型与三角形的等效变换概述在电路分析中,星型电阻网络由三个电阻分支组成,形状类似于星型,而三角形电阻网络由三个电阻分支组成,形状类似于三角形。
当需要对这样的电阻网络进行分析时,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,从而简化电路分析的复杂度。
2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。
通过合并相邻的电阻,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络。
这种等效变换的原理在于保持电路中的等效电阻值不变,从而简化电路分析的过程。
3. 电阻的星型与三角形的等效变换例题分析举例来说,对于一个星型电阻网络,我们可以按照以下步骤将其转换为等效的三角形电阻网络:- 合并星型电阻网络中的相邻电阻,得到等效的三角形电阻网络;- 计算等效的三角形电阻网络的总电阻值。
类似地,对于一个三角形电阻网络,我们可以按照以下步骤将其转换为等效的星型电阻网络:- 合并三角形电阻网络中的相邻电阻,得到等效的星型电阻网络;- 计算等效的星型电阻网络的总电阻值。
通过以上步骤,我们可以将星型与三角形电阻网络之间进行等效变换,从而简化电路分析的过程。
4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中,电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。
以电子电路设计为例,当需要对复杂的电路进行分析与设计时,可以利用星型与三角形的等效变换,将复杂的电路结构简化为更容易分析的形式,从而提高电路设计的效率与精度。
电阻的星形与三角形的等效变换例题电阻的星形与三角形的等效变换是电路分析中常见的问题。
通过等效变换,可以简化复杂的电路结构,使得对电路的分析和计算更加方便和高效。
在本文中,我将针对电阻的星形与三角形的等效变换例题展开讨论,从浅入深地探讨这一主题,帮助您更全面地理解电路分析中的等效变换方法。
1. 电阻的星形与三角形在电路分析中,星形与三角形是两种常见的电阻连接方式。
在星形连接中,三个电阻以一端共同连接在一起,另一端分别连接到电路的其余部分;而在三角形连接中,三个电阻以一端各自连接在一起,另一端也分别连接到电路的其余部分。
针对这种电阻连接方式,我们需要探讨如何进行等效变换,从而简化电路的分析过程。
2. 电阻的星形与三角形的等效变换我们来看一道例题:如何将一个包含星形连接的电阻网络转换为等效的三角形连接?这个问题就涉及到了电路分析中的等效变换方法。
通过分析电路结构和使用等效变换公式,我们可以将星形连接的电阻网络转化为等效的三角形连接,从而简化电路结构,使得后续的计算更加方便和直观。
这个过程需要我们对等效变换公式有深入的理解,以及对电路连接方式的分析能力。
3. 案例分析举一个具体的例子来说明:假设我们有一个包含星形连接的电阻网络,我们需要将其转化为等效的三角形连接。
我们可以根据等效变换的公式,利用电阻的数学关系和连接方式,逐步推导出等效的三角形连接电阻值。
在这个过程中,我们需要考虑电阻之间的串并联关系,以及星形与三角形连接的特点,从而正确地进行等效变换。
4. 总结与回顾通过本文的讨论,我们深入探讨了电阻的星形与三角形的等效变换例题,以及在电路分析中的重要意义。
我们从简到繁地分析了等效变换的原理和方法,帮助您更全面地理解了这一主题。
在深入讨论等效变换的过程中,我们强调了公式推导、案例分析和结论总结的重要性,以及对电路连接方式的理解和分析能力。
5. 个人观点和理解在我看来,电阻的星形与三角形的等效变换是电路分析中的重要内容,它帮助我们简化复杂的电路结构,提高分析和计算的效率。
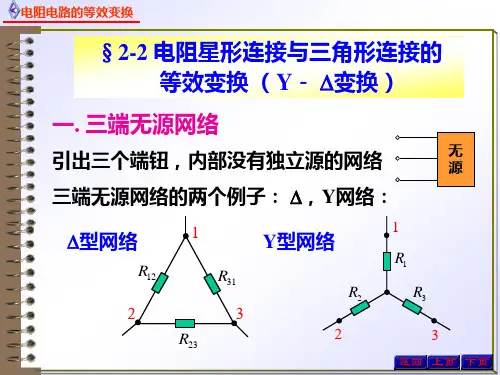
电阻的星形和三角形连接的等效变换之马矢奏春创作1、电阻的星形和三角形连接三个电阻元件首尾相连接,连成一个封闭的三角形,三角形的三个顶点接到外部电路的三个节点,称为电阻元件的三角形连接简称△连接,如图 2.7(a )所示。
三个电阻元件的一端连接在一起,另一端分别连接到外部电路的三个节点,称为电阻元件的星形连接,简称Y 形连接,如图2.7(b )所示。
三角形连接和星形连接都是通过三个节点与外部电路相连,它们之间的等效变换是要求它们的外部特性相同,也就是当它们的对应节点间有相同的电压12U 、23U 、31U 时,从外电路流入对应节点的电流1I 、2I 、3I 也必须分别相等,即Y-△变换的等效条件。
一种简单的推导等效变换方法是:在一个对应端钮悬空的同等条件下,分别计算出其余两端钮间的电阻,要求计算出的电阻相等。
悬空端钮3时,可得:12233112122331()R R R R R R R R ++=++ 悬空端钮2时,可得:31122331122331()R R R R R R R R ++=++悬空端钮1时,可得:23123123122331()R R R R R R R R ++=++ 联立以上三式可得:123111223311223212233131233122331R R R R R R R R R R R R R R R R R R =++=++=++ (2-2)式(2-2)是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。
从式(2-2)可解的:121212323232313131312R R R R R R R R R R R R R R R R R R =++=++=++ (2-3)以上互换公式可归纳为:当Y 形连接的三个电阻相等时,即123Y R R R R ===,则等效△形连接的三个电阻也相等,它们等于1223313Y R R R R R ∆==== 或 1=3Y R R ∆ (2-4)。
电阻的星形和三角形连接的等效变换
1、电阻的星形和三角形连接
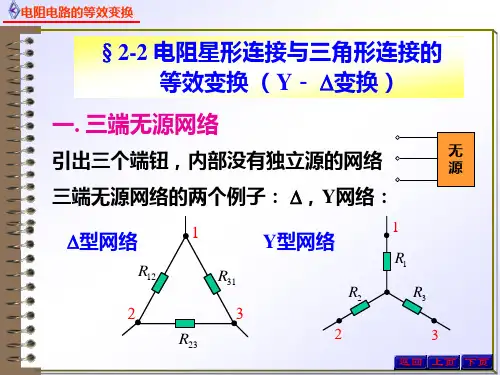
三个电阻元件首尾相连接,连成一个封闭的三角形,三角形的三个顶点接到外部电路的三个节点,称为电阻元件的三角形连接简称△连接,如图2.7(a )所示。
三个电阻元件的一端连接在一起,另一端分别连接到外部电路的三个节点,称为电阻元件的星形连接,简称Y 形连接,如图2.7(b )所示。
三角形连接和星形连接都是通过三个节点与外部电路相连,它们之间的等效变换是要求它们的外部特性相同,也就是当它们的对应节点间有相同的电压12U 、23U 、31U 时,从外电路流入对应节点的电流1I 、2I 、3I 也必须分别相等,即Y-△变换的等效条件。
一种简单的推导等效变换方法是:在一个对应端钮悬空的同等条件下,分别计算出其余两端钮间的电阻,要求计算出的电阻相等。
悬空端钮3时,可得:12233112122331()R R R R R R R R ++=
++ 悬空端钮2时,可得:31122331122331()R R R R R R R R ++=
++ 悬空端钮1时,可得:23123123122331
()R R R R R R R R ++=++ 联立以上三式可得:1231112233112232122331
3123
3122331R R R R R R R R R R R R R R R R R R =
++=++=
++ (2-2)
式(2-2)是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。
从式(2-2)可解的:
1212123232323131
31312R R R R R R R R R R R R R R R R R R =++
=++
=++ (2-3)
以上互换公式可归纳为:
=Y ∆∆形相邻电阻的乘积
形电阻形电阻之和
=
Y ∆形电阻两两乘积之和
形电阻Y 形不相邻电阻 当Y 形连接的三个电阻相等时,即123Y R R R R ===,则等效△形连接的三个电阻也相等,它们等于
1223313Y R R R R R ∆==== 或
1=3Y R R ∆ (2-4) 如有侵权请联系告知删除,感谢你们的配合!。