当前位置：文档之家 › 高数函数图形的描绘

高数函数图形的描绘

  • 格式：ppt
  • 大小：1.86 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

高等数学——函数图形的描绘

高等数学——函数图形的描绘

函数图形的描绘在中学时我们用描点法来作函数的图像，这种方法常遗漏曲线的一些关键点，如极值点、拐点等，使得函数的一些重要性态难以准确地显示出来。

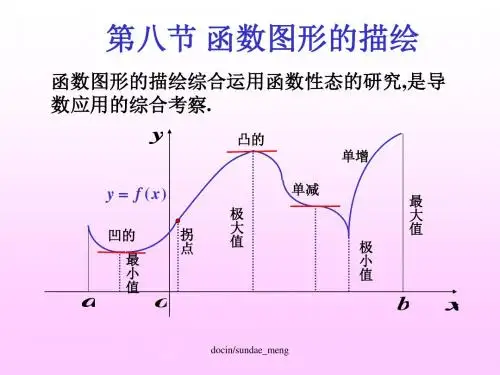
在本章前两节我们借助于导数的符号讨论了函数图形的升降和凹凸，以及在什么地方有极值点，什么地方有拐点，这样也就基本掌握了函数的性态，并把函数的图形画得比较准确。

此外，为了描绘函数图形在无穷远处的走势，还有必要讨论函数图形在无穷远处的变化趋势，即渐近线。

一、渐近线1、定义定义 若曲线)(x f y =上一动点沿着曲线无限远去时，该点与某条定直线L 的距离趋于零，则称直线L 为曲线)(x f y =的渐近线（如图153--）。

2、分类渐近线可分为水平渐近线、铅直渐近线和斜渐近线。

（1）水平渐近线 若函数)(x f y =的定义域为无穷区间，且C x f x =∞→)(lim （或C x f x x =-∞→+∞→)(lim )(） 图153--则称直线C y =为曲线)(x f y =的水平渐近线。

例如，因为01lim=∞→x x ，故直线0=y 为曲线xy 1=的水平渐近线；又如，因为2arctan lim π=+∞→x x ，2arctan lim π-=-∞→x x ，故直线2π=y 及直线2π-=y 均为曲线x y arctan =的水平渐近线。

（2）铅直渐近线 若函数)(x f y =在点0x 处间断，且∞=→)(lim 0x f x x则称直线0x x =为曲线)(x f y =的铅直渐近线。

注：铅直渐近线定义式∞=→)(lim 0x f x x 中，0x x →可换作-→0x x 或+→0x x ，∞→)(x f 亦可换作-∞→)(x f 或+∞→)(x f 。

例如，因为∞=→x x 1lim0，故直线0=x 为曲线xy 1=的铅直渐近线；又如，因为-∞=+→x x ln lim 0，故直线0=x 为曲线x y ln =的铅直渐近线。

*（3）斜渐近线 设有函数)(x f y =，若0)]()([lim =+-∞→b ax x f x则称直线b ax y +=为曲线)(x f y =的斜渐近线，其中xx f a x )(lim∞→=，])([lim ax x f b x -=∞→注：若x x f x )(lim ∞→不存在，或虽然xx f x )(lim ∞→存在但])([lim ax x f x -∞→不存在，则可以断定)(x f y =不存在斜渐近线。

【中学课件】函数图形的描绘-PPT文档资料

【中学课件】函数图形的描绘-PPT文档资料

x( 2 ,0 ) 3 , 2 ) 2 ( , 3 ) 3 (
f (x)
0
不存在
(0 , )
f (x)
0 0
拐点
( 3, 26 ) 9

f ( x)
极值点
docin/sundae_meng
3
间 断 点
补充点 : ( 1 3 , 0 ), ( 1 3 , 0 );
y . 2
2、图形描绘的步骤
利用函数特性描绘函数图形.
第一步
y f ( x ) 确 定 函 数 的 定 义 域 , 利 用 函 数 奇 偶 性 、 周 期 性 缩 小 范 围 ;
确 定 特 殊 点 : 曲 线 与 x 轴 的 交 点 , 即 : f ( x ) = 0 ; ' " f ( x ) 0 f( x ) 0 使 和 及 导 数 不 存 在 的 点 .
第二步
docin/sundae_meng
用 特 殊 点 将 函 数 的 定 义 域 划 分 成 几 个 部 f'( x )和 分 区 间 , 列 成 表 格 .确 定 在 这 些 部 分 区 间 内 f" ( x ) 的 符 号 ， 并 由 此 确 定 函 数 的 增 减 性 、 极 值 和 函 数 的 凹 凸 性 和 拐 点 。
4 ( x 2 ) f ( x ) 3 , 4 ( x 1 ) x , lim f ( x ) lim [ 2 2 ] x 0 x 0 x 8 (x 3 ) f (x ) . 得铅直渐近线 x0 . 4 x
列表确定函数升降区间,凹凸区间及极值点和拐点:
docin/sundae_meng
3、作图举例

高数A上册3-6

高数A上册3-6

要点:
1. 曲线渐近线的求法 水平渐近线 ; 垂直渐近线. 2. 函数图形的描绘 按作图步骤进行.
令 y 0, 得 x 0，x 2 （驻点）
当 x 1, y不存在.
当 x 1,

( y的分界点）
y不存在.
( y的分界点）
x ( ,2) 2 (2,1) 1
f ( x )
(1,0)
0 (0, )
0

0


不存在 不存在 间断点
f ( x )
1 ) 2e
x2 2
0
极大值

1 2

(1,

0
拐点
1 ) 2e

1 lim ( x ) lim e x x 2
0, 得水平渐近线 y 0.
y
1
o
1
x
1 ( x ) e 2
x2 2
x2 1 例3 作函数 y 的图形. 或 y x 1 x 1 x 1
二、函数图形的描绘
变量之间的关系用函数来表达，作出函数的 图形就可以形象地看出变量之间的关系。 作图步骤：
1.确定函数的定义域 ,并考察其奇偶性及周期性 ; 2.讨论函数的单调性和极值 ;（用y判断）
4.确定曲线的渐近线; 5.描出某些特殊点，由此作出函数的图形 . 3.讨论曲线的凹凸性和拐点;（用y判断）

列表
例1 作函数 f ( x ) x 3 x 2 x 1 的图形.
解: 定义域 : (,), 无奇偶性及周期性.
f ( x) 3 x 2 2 x 1 (3 x 1)( x 1), 1 f ( x ) 6 x 2 6( x ). 3 1 令 f ( x ) 0, 得驻点 x , x 1. ( y的分界点） 3 1 令 f ( x ) 0, 得 x . ( y的分界点） 3

高等数学第四节 曲线凹凸性与拐点 函数图形描绘

高等数学第四节 曲线凹凸性与拐点 函数图形描绘
求其一、二阶导数，得
y 2xex2和y2ex2(2x21)，
令 y = 0. 得驻点 x = 0，
令 y = 0， 得 x 2 .
2
当 x 时 y 0， 所以 y = 0 为该函数图形 的水平渐近线.
讨论 y， y 的正负情况，确定函数 y e x2 的增减区间和极值，凹凸区间和拐点， 将上述结 果归结下表：
.
令 y = 0 得 x = -1， x = 1.
当 x (, -1) 时， y < 0，此区间是凸区间； 当 x (1, 1) 时， y > 0，此区间是凹区间； 当 x (1, + ) 时， y < 0，此区间是凸区间. 因为 f (-1) = f (1) = 0， f (x) 在点 x = - 1. x = 1 的两侧变号，且 f ( -1 ) = f ( 1 ) = ln2，所以点 (- 1, ln2) 和 (1, ln2)为拐点.
所以x直 1为 线曲 y线 1 的垂直.渐近 x1
y
y 1 x 1
O
1
x
(2) 水平渐近线 若limf(x)b, 或limf(x)b,
x
x
则称直线 y = b 为曲线 y = f (x) 的水平渐近线 .
例如，对于曲线 y 1 来说，
x 1
lim 1 0,
y
x x1
y

2x 和 x2 1
2(x2 1) y (x2 1)2 .
不难发现，该函数在定义域内无驻点，也
没有极值点.
通 过y对 和y正 负 情 况 的 讨函 论数 ， 确 的增、减区间凹 和凸 极区 值间 ，和 . 拐点
将上述结果归结下表：

高等数学3.4 曲线的凹凸性与拐点 函数图形的描绘

高等数学3.4 曲线的凹凸性与拐点 函数图形的描绘
本题也可以下表给出解答：
x f (x) f (x)
( , 2)
2 0
拐点(2, 3)
(2, + ) +
其中 ， 分别表示曲线凸和凹.
例 4 讨论曲线 y = ln(1 + x2) 的凹凸区间与拐点. 解 定义域为( , ). 因为
y 2x , 1 x2
y

2(1 x 2 ) (1 x 2 )2
O1
x
-1
曲线 y x3 是凹的．
所以，点(0,0) 为曲线 y x3 的拐点．
例 3 讨论曲线 f (x) = x3 - 6x2 + 9x + 1 的凹凸 区间与拐点．
解 定义域为( , ).
因为
f (x) = 3x2 - 12x + 9，
f (x) = 6x - 12 = 6(x - 2 )， 令 f (x) = 0，可得 x = 2.
当 x ( , 2) 时，f (x) < 0， 此区间是凸区间． 当 x (2, + ) 时，f (x) > 0， 此区间是凹区间．
当 x = 2 时， f (x) = 0，因 f (x) 在 x = 2 的两 侧变号，而 f (2) = 3， 所以 (2, 3)是该曲线的拐点.
(2) 用上述各点按照从小到大依次将(a,b) 分成小 区间,再在每个小区间上考察 f (x) 的符号；
(3) 若 f (x) 在某点 xi 两侧近旁异号，则(xi , f (xi )) 是曲线y = f (x)的拐点，否则不是．
例 2 曲线 y x3的定义域为(,)，画其草图．
则称直线
x = x0近线.
例如， 对于曲线 y = ln x 来说， 因为

高等数学入门——描绘函数图像的一般步骤及例子

高等数学入门——描绘函数图像的一般步骤及例子

高等数学入门——描绘函数图像的一般步骤及例子高等数学是大学数学的基础课程之一，其重要内容之一是描绘函数的图像。

描绘函数图像的一般步骤如下：1.确定定义域和函数的类型：首先需要确定函数的定义域，即函数可以取值的范围。

同时，需要确定函数是一元函数还是多元函数，是线性函数还是非线性函数等。

2.求导或求导数的一般规律：对于一元函数，可以通过求导的方法来描绘函数的变化趋势。

求导可以确定函数的关键点，如极值点、拐点等。

对于多元函数，则需要利用偏导数来确定函数的变化趋势。

3.确定增减、凹凸和拐点：通过求导或偏导数，可以确定函数的单调性和凹凸性。

当导数为正时，函数单调递增；当导数为负时，函数单调递减。

当二阶导数大于零时，函数凹，小于零时函数凸。

4.确定函数的特殊点：特殊点包括与坐标轴的交点、零点、无穷大点等。

这些点是函数图像的关键部分，需要特别关注。

5.确定函数的渐近线：渐近线是函数图像在无穷远点的变化趋势。

有水平渐近线、垂直渐近线和斜渐近线等。

下面举例说明：例子1：绘制函数y=x^2-2x+1首先，确定定义域和函数的类型：该函数为一元二次函数，定义域为实数集。

然后，求导：y'=2x-2接着，确定增减、凹凸和拐点：当x<1时，y'<0，函数递减；当x>1时，y'>0，函数递增；令y'=0，则x=1，该点为拐点。

继续求二阶导数：y''=2可以确定函数为凹函数。

然后，确定函数的特殊点：与x轴的交点为y=0，即x=1；与y轴的交点为x=0。

最后，确定函数的渐近线：无垂直渐近线；当x趋于无穷大时，y趋于无穷大，可以确定y轴为水平渐近线。

综上所述，根据以上步骤，我们可以描绘出函数y=x^2-2x+1的图像。

例子2：绘制函数 y = sin(x) / x首先，确定定义域和函数的类型：该函数为一元函数，定义域为实数集，但要注意x≠0。

然后，求导：y' = (x*cos(x) - sin(x)) / x^2接着，确定增减、凹凸和拐点：当x<0时，y'>0，函数递增；当x>0时，y'<0，函数递减；令 y' = 0，则 x = tan(x)，求解该方程需要使用数值逼近法得到近似解。

高等数学-函数图形的描绘

高等数学-函数图形的描绘
+1
= ∞，
所以直线 = −1是曲线 =
1
的垂直渐近线.
+1
9
本节内容
01 渐近线
02 描绘函数图形
10
02 描绘函数图形
描绘函数图形的步骤：
（1）确定函数 = ()的定义域；
（2）讨论函数的奇偶性、周期性，确定函数图形的对称特征；
（3）讨论函数图形的单调性和凹凸性，并求出函数的极值和拐点；
为曲线 = ()的水平渐近线.
注 水平渐近线最多有两条.
3
01 渐近线
例1 求曲线 = 的水平渐近线.
解 因为 = 0,
→−∞
所以直线 = 0是曲线 = 的水平渐近线.
4
例2 求曲线 =
解
1
因为
→∞ +1
1
的水平渐近线.
+1
= 0，
2. 垂直渐近线
垂直渐近线
若函数 = ()在0 的某去心邻域（或左侧邻域，或右
侧邻域）内有定义，当 () = ∞（或 − = ∞
→0
→0
或 + () = ∞）时，则称直线 = 0 为曲线 =
→0
的垂直渐近线.
注 1.垂直渐近线可以有无数条.
所以直线 = 0是曲线 =
1
的水平渐近线.
+1
5
01 渐近线
例3 求曲线 = 的水平渐近线.
解 因为 =
→+∞
=
→−∞
所以直线 =

和
2
=

，
2

− ，
2

− 是曲线
2

高等数学 上、下册3_6 函数图形的描绘

高等数学 上、下册3_6 函数图形的描绘
1. 曲线渐近线的求法
铅直渐近线
2. 函数图形的描绘 按作图步骤进行
作业
P141 1, 3(3), (4)
渐近线来描绘.
定义 若 lim f (x) A或 lim f (x) A，则直线 y A是曲
x
x
线 y f (x)的水平渐近线.
若 lim x x0
f
(x) 或 lim x x0
f
(x) ，直线 x
x0是曲线 y
f (x)
的铅直渐近线.
例如，因为 lim 1 ， lim 1 0 ，所以直线 x 0是曲线
3
3
曲 线 为 凹 的 .当 x 1 时 ， y 16 .故 (1 , 16 ) 为 拐 点 .
3
27 3 27
（ 4） limf(x).曲 线 没 有 渐 近 线 . x
（ 5） yx3x2x1(x1)2(x1).当 x1时 ， y0.当 x0时 ， y1.曲 线 与 x轴 交 于 点 (1,0)及 (1,0)， 与 y轴 交 于 点 (0,1).极 大 值 yx10.
例 1 描 绘 函 数 y x 3 x 2 x 1 的 图 形 .
解 （ 1） 函 数 定 义 域 为(,)
（ 2） y 3 x 2 2 x 1 (3 x 1)( x 1) ， 驻 点 x 1 , x 1 将 3
定 义 域 分 为 ( , 1 ),( 1 ,1),(1,+ )，在 ( , 1 ),(1,+ )内 ，
x0 x
x x
y 1 的一条铅直渐近线，直线 y 0是曲线的一条水平渐近线 x
（图 3-9）
又如，因为
lim
x
ex x2 1
0 ， lim x1

高数 第三节 曲线的凹凸性和函数图形的描绘

高数 第三节 曲线的凹凸性和函数图形的描绘

y 2 e
(1 2 x 2 )
1
( 1 ,1 e ) 2
1 2
(
1 ,1 e 2 2
1
)
o
x
机动
目录
上页
下页
返回
结束
备用题 求笛卡儿叶形线 x 3 y 3 3a x y 的渐近线 . 解: 令 y = t x , 代入原方程得曲线的参数方程 :
3a t2 3a t , y x t 1 3 3 1 t 1 t 当x 时t 1, 因 y 3a t2 3a t 1 lim lim t 1 1 t 3 x x 3 1 t 3a t2 3a t 3 at (1 t ) lim y ( x) lim lim (1t )(1t t 2 ) 3 3 x t 1 1 t t 1 1 t a 所以笛卡儿叶形线有斜渐近线 y x a
机动
x1x x1 x1x2x2x2 xx x2 x 1 2 2
目录 上页 下页 返回 结束
定义2 . 设函数
在区间 I 上连续 ,
(1) 若曲线弧位于其上每一点处切线的上方， 则称f(x)图形是凹的; (2) 若曲线弧位于其上每一点处切线的下方， y y 则称f(x)图形是凸的 . y 连续曲线上有切线的凹凸分界点
2) 求拐点可疑点坐标
令 y 0 得 x1 0 , x2 2 , 对应 y1 1 , y2 11 3 27 2 3 3) 列表判别
x ( , 0) y y 凹
0 0 1
(0 , 2 ) 3

( 2 , ) 3 0
2 3 11 27
凸
凹
( , 0) 及 ( 2 , ) 上向上凹, 在 (0 , 2 ) 上 故该曲线在 3 3 点 ( 0 , 1 ) 及 ( 2 , 11 ) 均为拐点. 向上凸 , 3 27

高等数学3.8 函数图形的描绘

高等数学3.8 函数图形的描绘

4 极大


11/3 拐点
0

6
(6，)

x (，3) f (x) f (x) f (x)
(3，3)

3 0
(3，6)
6 0
4 极大



(6，)
11/3 拐点

(5) x = 3是曲线的铅直渐近线，y = 1是曲线的水平渐近线； 补充f(1)8， f(9)8， f(15)11/4； (6)特殊点：f(0)1． y (7)绘图． x = 3 36 x (3,4) 11 y 1 ( x 3) 2 (6, ) 3 3 y=1
最后按照曲线的性态逐段描绘．
例1 画出函数yx 3x 2x1的图形． 解 (1)函数的定义域为(，)， (2) f (x)3x22x1(3x1)(x1)，f (x)6x22(3x1)． 驻点为x 1/3和x1；二阶导数为零的点为x 1/3． (3)列表分析： x (,1/3) 1/3 (1/3,1/3) 1/3 + 0 ຫໍສະໝຸດ 画函数的图形都要考虑什么？
描绘函数图形的一般步骤： (1)确定函数的定义域；
(2)观察函数y=f(x)是否具有奇偶性、周期性；
(3)求出一阶、二阶导数为零的点和一阶、二阶导数不存在 的点；
(4)列表， 确定曲线的单调性、极值点和极值，确定曲线的
凹凸性和拐点； (5)确定曲线有无渐近性； (6)确定一些特殊点(曲线与坐标轴的交点等); (7)在直角坐标系中，描出所有关键性的点，画出渐近线，
y
ye
x2
2
1
0
1
2
x
观察与思考： 观察函数的图形，在图形上有哪些关键的点？关键点的两 侧(或两点间)曲线有什么特点？ 函数的图形有无渐近线？有无 对称性？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x x x k lim f (x)
x x
(或 x )
lim [ f (x) k b ] 0
x x
x
b lim [ f (x) k x]
x (或 x )
1/16/2020
例2. 求曲线
的渐近线.
y
解:

y
x3
,
(x 3)(x 1)
(拐点)
1/16/2020
x 0 (0, 1) 1 (1, )
y 0

y
0

y
1 2π
1 2πe
(极大)
(拐点)
4) 求渐近线
lim y 0
x
y 0 为水平渐近线
5) 作图
y
1 2π
A
y0 O
y
1
x2
e2
2π
B
1
x
1/16/2020
内容小结
1. 曲线渐近线的求法
2 2
1;
lim 1 x01

e e
x x
2 2

1/16/2020
2. 曲线 y 1 ex2 的凹区间是
( 1 , 1 )
22
,
凸区间是
( ,
lim y ,
x 3
(或 x 1)
3 O1 x
y x2
所以有铅直渐近线 x 3 及 x 1
又因
k
lim
x
f (x) x

lim
x
x2
x2 2x

3
b

lim [
x
f
(x)
x]

lim
x
2x2 3x x2 2x 3
y x 2为曲线的斜渐近线 .
L PN
有渐近线
x y0 ab
O
x
y
但抛物线
无渐近线 .
Ox
1/16/2020
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或 x )
若
则曲线
有铅直渐近线 x x0 .
(或 x x0 )
y
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2 x x 1
y 1 4 y 2(x 1)
令 y 0 得 x 1, 3 ;
1/16/2020
3) 判别曲线形态
x (, 1) 1
y
0
y
y
2
(1,1)
1 (1,3) 3

无
0
定
义
0
(3, )
(极大)
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
2
4 3
(极大)
(拐点)

2 3
(极小)
例4. 描绘方程
的图形.
解: 1) y (x 3)2 , 定义域为 4(x 1)
2) 求关键点. 原方程两边对 x 求导得
2(x 3) 4 y 4 y 4xy 0
①
y x 3 2y 2(x 1)
①两边对 x 求导得 2 4 y 8y 4xy 0
水平渐近线 ; 垂直渐近线;
斜渐近线
2. 函数图形的描绘
按作图步骤进行
1/16/2020
思考与练习
1.
曲线
y

1 1

ex2 ex2
(A) 没有渐近线；
(D )
(B) 仅有水平渐近线；
(C) 仅有铅直渐近线；
(D) 既有水平渐近线又有铅直渐近线.
提示:
lim
x
1 1

e e
x x
lim 5x 9 5 x 4(x 1) 4
y 1 x 5 为斜渐近线 44
5) 求特殊点 x 0 2 y 9 1 44
y (x 3)2 4(x 1)
y

(
x 4(
3)(x x 1)2
1)
y

(x
2 1)3
1/16/2020
6）绘图
x (, 1) 1 (1,1)
无对称性及周期性.
2) y x2 2x, y 2x 2,
y
令 y 0,
令 y 0,
1 O 1 2 3 x
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
y
0
0
y y
x 1 3
4)
y2
3
2
1/16/2020
0
图形对称于 y 轴.
2) 求关键点
y
1 2π
x
e
x2 2
,
y
1
e

x2 2
(1

x
2
)
2π
令 y 0 得 x 0; 令 y 0 得 x 1
3) 判别曲线形态
x 0 (0, 1) 1 (1, )
y 0

y
0

y
1 2π
1 2πe
(极大)
第六节 函数图形的描绘
一、 曲线的渐近线 二、 函数图形的描绘
1/16/2020
一、 曲线的渐近线
定义 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为
曲线C 的渐近线 .
y
y f (x)
或为“纵坐标差” C M
y kxb
例如, 双曲线
2
x
O1
y 2 为水平渐近线; lim( 1 2) , x 1为铅直渐近线.
x1 x 1
1/16/2020
2. 斜渐近线 ( P76 题14)
若
(kx b)
(或 x )
(kx b)
lim x [ f (x) k b ] 0
x
x
x
斜渐近线 y kx b. k lim [ f (x) b ]
1/16/2020
二、函数图形的描绘
步骤 :
1. 确定函数 期性 ;
的定义域 , 并考察其对称性及周
2. 求
并求出 及
为 0 和不存在
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
1/16/2020
例3. 描绘
的图形.
解: 1) 定义域为
y
2
(极大)
铅直渐近线 x 1
斜渐近线
y1x5 44
特殊点
x0 y 9
2 1
44
1 (1,3) 3 (3, )
无
0
定 义
(极小)
y
y (x 3)2
4(x 1)
2 1
O12 3 5 x
y

1 4
x

5 4
x 1
1/16/2020
例5. 描绘函数
的图形.
解: 1) 定义域为
x1
y (x 3)2 , 4(x 1)yFra bibliotek(
x 4(
3)(x x 1)2
1)
,
y

(
x
2 1)3
1/16/2020
又因
lim y 1 , 即 k 1
x x 4
4
b lim ( y 1 x) lim [(x 3)2 1 x] x 4 x 4(x 1) 4