第五节--函数图形的描绘
- 格式:doc
- 大小:455.00 KB
- 文档页数:4






高等数学入门——描绘函数图像的一般步骤及例子高等数学是大学数学的基础课程之一,其重要内容之一是描绘函数的图像。
描绘函数图像的一般步骤如下:1.确定定义域和函数的类型:首先需要确定函数的定义域,即函数可以取值的范围。
同时,需要确定函数是一元函数还是多元函数,是线性函数还是非线性函数等。
2.求导或求导数的一般规律:对于一元函数,可以通过求导的方法来描绘函数的变化趋势。
求导可以确定函数的关键点,如极值点、拐点等。
对于多元函数,则需要利用偏导数来确定函数的变化趋势。
3.确定增减、凹凸和拐点:通过求导或偏导数,可以确定函数的单调性和凹凸性。
当导数为正时,函数单调递增;当导数为负时,函数单调递减。
当二阶导数大于零时,函数凹,小于零时函数凸。
4.确定函数的特殊点:特殊点包括与坐标轴的交点、零点、无穷大点等。
这些点是函数图像的关键部分,需要特别关注。
5.确定函数的渐近线:渐近线是函数图像在无穷远点的变化趋势。
有水平渐近线、垂直渐近线和斜渐近线等。
下面举例说明:例子1:绘制函数y=x^2-2x+1首先,确定定义域和函数的类型:该函数为一元二次函数,定义域为实数集。
然后,求导:y'=2x-2接着,确定增减、凹凸和拐点:当x<1时,y'<0,函数递减;当x>1时,y'>0,函数递增;令y'=0,则x=1,该点为拐点。
继续求二阶导数:y''=2可以确定函数为凹函数。
然后,确定函数的特殊点:与x轴的交点为y=0,即x=1;与y轴的交点为x=0。
最后,确定函数的渐近线:无垂直渐近线;当x趋于无穷大时,y趋于无穷大,可以确定y轴为水平渐近线。
综上所述,根据以上步骤,我们可以描绘出函数y=x^2-2x+1的图像。
例子2:绘制函数 y = sin(x) / x首先,确定定义域和函数的类型:该函数为一元函数,定义域为实数集,但要注意x≠0。
然后,求导:y' = (x*cos(x) - sin(x)) / x^2接着,确定增减、凹凸和拐点:当x<0时,y'>0,函数递增;当x>0时,y'<0,函数递减;令 y' = 0,则 x = tan(x),求解该方程需要使用数值逼近法得到近似解。
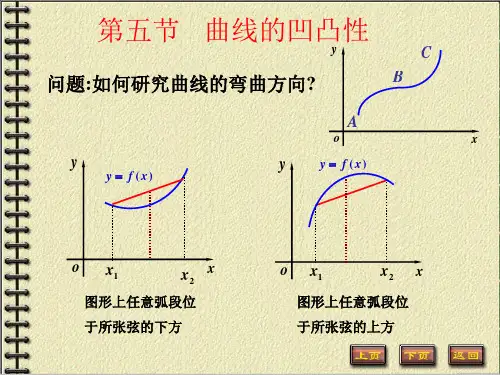




函数图形的描绘分布图示★ 引言★ 渐近线 ★ 例1 ★ 函数图形描绘的步骤★ 例2 ★ 例3 ★ 例4 ★ 例5★ 内容小结 ★ 课堂练习 ★ 习题3-6 ★ 返回内容要点一、渐近线的概念 水平渐近线 铅直渐近线 斜渐近线;二、函数图形的描绘:对于一个函数,若能作出其图形,就能从直观上了解该函数的性态特征,并可从其图形清楚地看出因变量与自变量之间的相互依赖关系. 在中学阶段,我们利用描点法来作函数的图形. 这种方法常会遗漏曲线的一些关键点,如极值点、拐点等. 使得曲线的单调性、凹凸性等一些函数的重要性态难以准确显示出来. 本节我们要利用导数描绘函数)(x f y =的图形,其一般步骤如下:第一步 确定函数)(x f 的定义域, 研究函数特性如: 奇偶性、周期性、有界性等, 求出函数的一阶导数)(x f '和二阶导数)(x f '';第二步 求出一阶导数)(x f '和二阶导数)(x f ''在函数定义域内的全部零点,并求出函数)(x f 的间断点和导数)(x f '和)(x f ''不存在的点, 用这些点把函数定义域划分成若干个部分区间;第三步 确定在这些部分区间内)(x f '和)(x f ''的符号, 并由此确定函数的增减性和凹凸性,极值点和拐点;第四步 确定函数图形的水平、铅直渐近线以及其它变化趋势;第五步 算出)(x f '和)(x f ''的零点以及不存在的点所对应的函数值,并在坐标平面上定出图形上相应的点;有时还需适当补充一些辅助作图点(如与坐标轴的交点和曲线的端点等); 然后根据第三、四步中得到的结果,用平滑曲线联接而画出函数的图形.例题选讲求曲线渐近线例1(E01) 求1)3)(2(2)(-+-=x x x x f 的渐近线.解 易见函数)(x f 的定义域为).,1()1,(+∞-∞ ,)(lim 1-∞=+→x f x ,)(lim 1+∞=-→x f x1=∴x 是曲线的铅直渐近线.又x x f x )(lim ∞→ )1()3)(2(2lim -+-=∞→x x x x x ,2=⎥⎦⎤⎢⎣⎡--+-∞→x x x x x 21)3)(2(2lim 1)1(2)3)(2(2lim ---+-=∞→x x x x x x ,4= 42+=∴x y 是曲线的一条斜渐近线.例2(E02) 按照以下步骤作出函数()10434+-=x x x f 的图形.(1) 求()x f '和()x f '';(2) 分别求()x f '和()x f ''的零点;(3) 确定函数的增减性、凹凸性、极值点和拐点; (4) 作出函数()10434+-=x x x f 的图形.解 (1) ()23124x x x f -=',()x x x f 24122-=''.(2) 由()012423=-='x x x f ,得到0=x 和3=x .由()024122=-=''x x x f ,得到0=x 和2=x .(4) 算出0=x ,2=x ,3=x 处的函数值()100=f ,()62-=f ,()173-=f .根据以上结论,用平滑曲线连接这些点,就可以描绘函数的图形.例3 作函数1)(23+--=x x x x f 的图形. 解 定义域为),,(+∞-∞无奇偶性及周期性. ),1)(13()(-+='x x x f ).13(2)(-=''x x f令,0)(='x f 得,3/1-=x .1=x 令,0)(=''x f 得.3/1=x 列表综合如下:51015---51015-11234O xy补充点: ),0,1(A ),1,0(B .85,23⎪⎭⎫⎝⎛C 综合作出图形.函数作图例4 (E03) 作函数2)1(4)(2-+=x x x f 的图形.解 ,0:≠x D 非奇非偶函数,且无对称性.,)2(4)(3x x x f +-='.)3(8)(4xx x f +='' 令,0)(='x f 得;2-=x 令,0)(=''x f 得.3-=x)(lim x f x ∞→⎥⎦⎤⎢⎣⎡-+=∞→2)1(4lim 2x x x ,2-= 得水平渐近线;2-=y )(lim 0x f x →⎥⎦⎤⎢⎣⎡-+=→2)1(4lim 20x x x ,+∞= 得铅直渐近线.0=x 列表综合如下: 补充点: ),0,31(-);0,31(+ ),2,1(--A ),6,1(B ).1,2(C作出图形例5 (E04) 作函数 2221)(x ex -=πϕ的图形.解 函数定义域),,(+∞-∞且.4.021)(0≈≤<πϕx偶函数,图形关于y 轴对称.,2)(22x ex x --='πϕ.2)1)(1()(22x ex x x --+=''πϕ令,0)(='x ϕ得驻点,0=x 令,0)(=''x ϕ得特殊点,1-=x .1=x)(lim x x ϕ∞→ 2221limx x e-∞→=π,0=得水平渐近线.0=y列表确定函数升降区间,凹凸区间及极值点与拐点:综合作出图形。
第五节 函数图形的描绘
分布图示
★ 引言 ★ 渐近线 ★ 函数图形描绘的步骤 ★ 例1
★ 例2 ★ 例3 ★ 例4
★ 内容小结 ★ 课堂练习 ★ 习题3-5
内容要点
一、渐近线的概念 水平渐近线 铅直渐近线 斜渐近线;
二、函数图形的描绘:对于一个函数,若能作出其图形,就能从直观上了解该函数的性态特征,并可从其图形清楚地看出因变量与自变量之间的相互依赖关系. 在中学阶段,我们利用描点法来作函数的图形. 这种方法常会遗漏曲线的一些关键点,如极值点、拐点等. 使得曲线的单调性、凹凸性等一些函数的重要性态难以准确显示出来. 本节我们要利用导数描绘函数)(x f y =的图形,其一般步骤如下:
第一步 确定函数)(x f 的定义域, 研究函数特性如: 奇偶性、周期性、有界性等, 求出函数的一阶导数)(x f '和二阶导数)(x f '';
第二步 求出一阶导数)(x f '和二阶导数)(x f ''在函数定义域内的全部零点,并求出函数)(x f 的间断点和导数)(x f '和)(x f ''不存在的点, 用这些点把函数定义域划分成若干个部分区间;
第三步 确定在这些部分区间内)(x f '和)(x f ''的符号, 并由此确定函数的增减性和凹凸性,极值点和拐点;
第四步 确定函数图形的水平、铅直渐近线以及其它变化趋势;
第五步 算出)(x f '和)(x f ''的零点以及不存在的点所对应的函数值,并在坐标平面上定出图形上相应的点;有时还需适当补充一些辅助作图点(如与坐标轴的交点和曲线的端点等); 然后根据第三、四步中得到的结果,用平滑曲线联接而画出函数的图形.
例题选讲
求曲线渐近线
例1 作函数1)(23+--=x x x x f 的图形. 解 定义域为),,(+∞-∞无奇偶性及周期性. ),1)(13()(-+='x x x f ).13(2)(-=''x x f
令,0)(='x f 得,3/1-=x .1=x 令,0)(=''x f 得.3/1=x 列表综合如下:
补充点: ),0,1(A ),1,0(B .85,23⎪⎭
⎫
⎝⎛C 综合作出图形.
例2(E01) 按照以下步骤作出函数()1043
4
+-=x x x f 的图形.
(1) 求()x f '和()x f '';
(2) 分别求()x f '和()x f ''的零点;
(3) 确定函数的增减性、凹凸性、极值点和拐点; (4) 作出函数()1043
4
+-=x x x f 的图形.
解 (1) ()2
3
124x x x f -=',()x x x f 24122
-=''.
(2) 由()01242
3
=-='x x x f ,得到0=x 和3=x .
由()024122
=-=''x x x f ,得到0=x 和2=x .
(4) 算出0=x ,2=x ,3=x 处的函数值
()100=f ,()62-=f ,()173-=f .
根据以上结论,用平滑曲线连接这些点, 就可以描绘函数的图形.
函数作图
例3 (E02) 作函数2)
1(4)(2
-+=x x x f 的图形.
解 ,0:≠x D 非奇非偶函数,且无对称性.
51015---51015
-11
2
3
4O x
y
,)2(4)(3x x x f +-
='.)
3(8)(4
x
x x f +='' 令,0)(='x f 得;2-=x 令,0)(=''x f 得.3-=x
)(lim x f x ∞→
⎥⎦
⎤
⎢⎣⎡-+=∞→2)1(4lim 2x x x ,2-= 得水平渐近线;2-=y )(lim 0x f x →⎥⎦
⎤
⎢⎣⎡-+=→2)1(
4lim 20x x x ,+∞= 得铅直渐近线.0=x 列表综合如下:
补充点: ),0,31(-);0,31(+ ),2,1(--A ),6,1(B ).1,2(C
作出图形
例4 (E03) 作函数 2
221)(x e
x -
=
π
ϕ的图形.
解 函数定义域),,(+∞-∞且.4.021)(0≈≤<πϕx
偶函数,图形关于y 轴对称.
,2)(2
2x e x x --
='π
ϕ.2)
1)(1()(2
2x e x x x --+=
''π
ϕ
令,0)(='x ϕ得驻点,0=x 令,0)(=''x ϕ得特殊点,1-=x .1=x
)(lim x x ϕ∞
→ 2
221lim
x x e
-
∞
→=π
,0=得水平渐近线.0=y
综合作出图形
课堂练习
1.两坐标轴0,0==y x 是否都是函数x
x
x f sin )(=的渐近线? 2.若函数)(x f 有,1)
(lim
,0)(lim ==-∞
→+∞
→x
x f x f x x ,)(lim ,0)
(lim ,2])([lim 2
∞===-→+∞→-∞→x f x x f x x f x x x 并且当)1,0(∈x 时, 0)(<'x f , 否则
),2(0)(≠>'x x f 当)2,2/1(∈x 时, 0)(>''x f , 否则),0(0)(≠<''x x f 则
(1) 函数)(x f 的单调区间(注明增减)是._______ (2) 函数曲线的凹向和拐点是._______
(3) 当_______=x 时, 函数取得极大值._______ (4) 函数的渐近线有._______。