23曲线的凹凸性、描绘函数图形
- 格式：ppt
- 大小：1.31 MB
- 文档页数：26
下载文档原格式
合集下载
《函数曲线的凹凸性》课件
《函数曲线的凹凸性》 ppt课件
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
CONTENTS 目录
• 引言 • 函数曲线的凹凸性判定 • 函数曲线的凹凸性性质 • 函数曲线的凹凸性与导数的关系 • 函数曲线的凹凸性与几何意义 • 总结与展望
CHAPTER 01
引言
凹凸性的定义
凹函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) geq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凹函数。
函数曲线的凹凸性可能会随着自变量x 的变化而发生变化。
凸函数曲线
表示函数图像呈上凸的几何形状，即 任意两点之间的连线位于曲线上方。
几何形状的凹凸性实例
下凹函数曲线
$f(x) = x^2$，$f(x) = sin x$
上凸函数曲线
$f(x) = log x$，$f(x) = e^x$
几何形状的凹凸性与生活中的应用
02
二次函数是典型的凹函数和凸函数，其图像为抛物 线。
03
指数函数和幂函数在其定义域内是凹函数，对数函 数在其定义域内是凸函数。
CHAPTER 04
函数曲线的凹凸性与导数的关系
导数与凹凸性的关系
01
导数大于0的区间内，函数曲线为 凹；
02
导数小于0的区间内，函数曲线为 凸。
导数在判断凹凸性中的应用
凸函数
对于函数$f(x)$，如果在区间$I$上，对于任意$x_1 < x_2$，都有$f(frac{x_1+x_2}{2}) leq frac{f(x_1) + f(x_2)}{2}$，则称$f(x)$在区间$I$上是凸函数。
23-曲线的凹凸性、描绘函数图形
趋于零 , 则称此直线 L 为曲线 y = f ( x ) 的一条 渐近线 .
曲 线 的 渐 近 线
水平渐近线
垂直渐近线
斜渐近线
水平渐近线
若 lim f ( x) b , 则曲线 f ( x) 有一条水平渐近线 y b .
x
这里的极限可以是
x
lim f ( x) b 或 lim f ( x) b .
x
垂直渐近线
若 lim f ( x) , 则曲线 y f ( x) 有一条垂直渐近线 x a .
x a
这里的极限可以是 xlim f ( x) , a lim lim f ( x) ; f ( x) ,
x a
x a
x a
lim f ( x) ; lim f ( x) .
f ( x) ( x 1) lim lim 1 2 x x x ( x 1) x
b k
现在给定一个函数 , 我们可以讨论它的：
定义域、 值 域、 奇偶性、 有界性、 周期性、 连续性、 间断点、 可微性、 单调性、 极 值、 最 值、 凹凸性、 拐 点、 渐近线、 零点位置 . 用极限讨论函数的变化趋势 . 用泰勒公式将函数离散化 .
三、函数图形的描绘
作函数图形的一般步骤如下： (1) 确定函数的定义域 , 观察奇偶性、周期性 . (2) 求函数的一、二阶导数 , 确定极值可疑点和拐点可疑点 .
若 f ( x) 在点 x0 两侧符号相反, 则
点 ( x0 , f ( x0 )) 为曲线 y f ( x) 的拐点 .
定理
( 判别拐点的充分条件 )
设 f ( x) C ( I ) , f ( x) 在 U( x0 ) ( x0 I ) 内三阶可导 .
经济数学课件 4.3函数的凹凸性
x
《经济数学基础》配套课件
定义4.3.3、4.3.4
若 lim f ( x) b，lim f ( x) b 或 lim f (x) b，
x
x
x
则称直线 y = b 为曲线 y = f (x) 的水平渐近线.
若 lim f (x) , lim f ( x) 或 lim f ( x) ，
0
0
f (x)
凹的∪
拐点 (0,1)
凸的∩
拐点 (2 3 ,1127)
凹的∪
凹区间为(,0《],经[2济3数,学基), 础凸》区配套间课为件[0, 2 3]
凹凸区间为(,0], [0, 2 3], [2 3 ,). 《经济数学基础》配套课件
例 求曲线
的拐点.
2
5
解:
y
1 3
x
3
,
y
2 9
x
3
x ( ,0) 0
2. 求
并求出 及
为 0 和不存在
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
《经济数学基础》配套课件
例5. 描绘函数
的图形.
解: 1) 定义域为
图形对称于 y 轴.
2)
求关键点 y 1
2
x
e
x2 2
,
y
1
e
x2
2 (1
(0, )
y
不存在
y凹
0
凸
因此点 ( 0 , 0 ) 为曲线
的拐点 .
《经济数学基础》配套课件
练习. 求曲线
的凹凸区间及拐点.
《函数凹凸性》PPT课件
y cos x sin x .
令 y 0,
得
x1
3 4
,
x2
7 4
.
f (3) 2 0, f (7) 2 0,
4
4
中值定理与导数的应用
10
在[0,2]内曲线有拐点为 (3 ,0), (7 ,0).
4
4
中值定理与导数的应用
11
二、渐近线
定义: 当曲线 y f ( x) 上的一动点 P 沿着曲线 移向无穷点时, 如果点 P 到某定直线 L 的距离 趋向于零, 那么直线 L 就称为曲线 y f ( x) 的 一条渐近线.
22
lim
x0
f
(x)
4( x 1)
lim[
x0
x2
2]
,
得铅直渐近线 x 0.
列表确定函数升降区间,凹凸区间及极值点和拐点:
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间
断 点
中值定理与导数的应用
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)(x 1), f ( x) 2(3x 1).
令 f ( x) 0, 得驻点 x 1 , x 1. 3
令 f ( x) 0,
得特殊点 x 1 . 3
补充点: A (1,0),
B (0,1), C (3 , 5). 28
f (x)在点 x0处二阶导数不存在 .
中值定理与导数的应用
6
例2 求曲线 y 3x4 4x3 1的拐点及
凹、凸的区间.
函数曲线的凹凸性与作图
（2）y
8
x3
5
x 3，y
8
5
x3
5
2
x 3，y
40 x
10
.
33
93 x
（3）令y 0，得x 1，又当x 0时，y不存在，故有表3 - 5所示的区间. 4
表3-5
函数曲线的凹凸性与作图
综上所述，判定曲线y f x的凹凸及拐点的步骤归纳如：
（1）求函数的定义域；
（2）求函数的一阶导数f x和二阶导数f x； （3）求出f x 0和f x不存在的点； （4）对步骤（3）求出的每一个点，检查其左、右邻近的f x的符号，如果异号，则该点为曲
（1）确定函数的定义域和值域； （2）确定曲线关于坐标轴的对称性； （3）求出曲线和坐标轴的交点； （4）判断函数的单调区间并求出极值； （5）判断函数的凹凸区间和拐点； （6）求出曲线的渐近线； （7）列表讨论并描绘函数的图像.
函数曲线的凹凸性与作图
例5
解
（1）定义无对称性.
0
曲线y f x的垂直渐近线(垂直于x轴).
（2）水平渐近线.对于曲线 y f x，若 lim f x A或 lim f x A,则直线y A是曲
x
x
线y f x的水平渐近线（平行于x轴）.
（3）斜渐近线 . 对于曲线y f x，若 lim f x a，lim[ f x ax] b，则直线 y ax b
定义2
若曲线C上的动点P沿曲线无限地远离原点时，动点P到某一固定直线L的距 离趋于零，则称直线L为曲线C的渐近线.
函数曲线的凹凸性与作图
曲线的渐近线有垂直渐近线、水平渐近线和斜渐近线三种.
（1）垂直渐近线.对于曲线y
f
3.5凹凸性与函数图形描绘PPT课件
3.5 曲线的凹凸性与函数作图
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导，
x0为I的任一内点，若对 x I( x x0 )，恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点，如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点，绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), （偶函数, 图形关于y轴对称）
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导，
x0为I的任一内点，若对 x I( x x0 )，恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点，如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点，绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), （偶函数, 图形关于y轴对称）
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
第四、六节 曲线凹凸性及函数图形描绘
x→x0 x→x0 x→x0
x 则 = x0是 数 = f ( x)的 条 直 近 . 函 y 一 垂 渐 线
y C o x y o
x0
x
曲 例1 求 线 y =
1 的 平 近 . 水 渐 线 x −1
y
2 1 -2 -1 -1 -2
y = ( x −1)
−1
1 解 Qlim =0 x→ x −1 ∞
1 一条水平渐近线 ∴ y = 0 是y = x −1
1 曲 的 垂 近 . 铅 渐 线 例2 求 线 y = x −1
O 1
2
x
1 1 解 Qlim = −∞, lim = +∞, − + x→ x −1 1 x→ x −1 1
∴x =1 y = f (x)的 条 垂 近 . 为 一 铅 渐 线
利用导数工具描绘函数的图形，称为分析法作图. 利用导数工具描绘函数的图形，称为分析法作图. 分析法作图
[ (2) f ′′( x) < 0, 则 ( x)在a,b]上的图形是凸的 f .
例1 判断函数 y = ln x的凹凸性 . 解 y 的定义域为 (0,+∞ )
1 Q y′ = x
y ′′ = − 1 x2
∴ 在(0， ∞ )内，有 y′′ < 0 +
例2 判断 y = x 3 的凹凸性 . 解
2 y ′′ = 36 x − 24 x = 36 x x − 令 y′′ = 0 3 列表
x2 =
2 3
x y" y
(−∞,0)
0 0
1(拐点)
2 , 0 3
+
－
0
11 (拐 ) 点 27
x 则 = x0是 数 = f ( x)的 条 直 近 . 函 y 一 垂 渐 线
y C o x y o
x0
x
曲 例1 求 线 y =
1 的 平 近 . 水 渐 线 x −1
y
2 1 -2 -1 -1 -2
y = ( x −1)
−1
1 解 Qlim =0 x→ x −1 ∞
1 一条水平渐近线 ∴ y = 0 是y = x −1
1 曲 的 垂 近 . 铅 渐 线 例2 求 线 y = x −1
O 1
2
x
1 1 解 Qlim = −∞, lim = +∞, − + x→ x −1 1 x→ x −1 1
∴x =1 y = f (x)的 条 垂 近 . 为 一 铅 渐 线
利用导数工具描绘函数的图形，称为分析法作图. 利用导数工具描绘函数的图形，称为分析法作图. 分析法作图
[ (2) f ′′( x) < 0, 则 ( x)在a,b]上的图形是凸的 f .
例1 判断函数 y = ln x的凹凸性 . 解 y 的定义域为 (0,+∞ )
1 Q y′ = x
y ′′ = − 1 x2
∴ 在(0， ∞ )内，有 y′′ < 0 +
例2 判断 y = x 3 的凹凸性 . 解
2 y ′′ = 36 x − 24 x = 36 x x − 令 y′′ = 0 3 列表
x2 =
2 3
x y" y
(−∞,0)
0 0
1(拐点)
2 , 0 3
+
－
0
11 (拐 ) 点 27
函数的性质曲线的凹凸性与分析作图法
9
1
y 10(x2)13 10
9
9
1 0[1
(x
2)3 ]
1
9( x 2)3
x1 3 时 y 0 ; x 2 2 时 y 不存在
(3)列表
1
y 10(x2)13 10
9
9
10[1
(x
2)3 ]
1
9( x 2)3
x1 3 时 y 0; x 2 2 时 y 不存在
x
(, 2) 2 (2,3) 3 (3, )
f (x)
0
0
f(x) f (x)
0
极大值
拐点
32 27
( 1 , 16 ) 3 27
y
极小值
0
B(0,1)
C (3,5) 28
A(1,0)
1
1 o 1
1
x
3
3
yx3x2x1
四、小结
函数图形的描绘综合运用函数性态的研究,是 导数应用的综合考察.
y
凸的
单增
yf(x)
极
凹的
拐 点
大 值
0
拐点
(3, 26) 9
极小值
3
lx i m f(x)lx i [m 4(x x 21)2]2, 得水平渐近 y线 2;
lx i0m f(x)lx i0[m 4(x x 21)2] ,得 垂 直 渐 近 线 x 0 .
补充点: (13 ,0 ),(13 ,0 );
A(1,2), 作图
B(1,6), C(2,1). y
1、 曲线 y e x 的水平渐近线为_______________.
2、 曲线 y 1 的水平渐近线为______________， x1
曲线的凹凸性与函数图象描绘
例3 当x
y时，e x
ey
x y
e 2 .
2
证：设f ( x) e x
f ( x) 0 f ( x)是凹的。
f ( x1 x2 )
f ( x1 )
f
(
x2
)
e
x1
2
x2
e x1
e x2
2
2
2
即当x
y时，e x
ey
x y
e 2 .
f ( x1 x2 ) f ( x1 ) f ( x2 ) ,
2
2
不 妨 设x1
x2 , 令x0
x1
2
x2
,
分别在[ x1 , x0 ]与[ x2 , x0 ]上
f (x)
f ( x0 )
f ( x0 )( x x0 )
1 2!
f ( )( x x0 )2
2
x2
)
1[ 2
f
( x1 )
f
( x2 )]
结论（2）可类似得证. 教材上用langrange定理证明!
例7 判断曲线 y x3 的凹凸性. 解 y 3x2, y 6x, 当x 0时， y 0,
曲线 在(,0]为凸的； 当x 0时， y 0, 曲线 在[0,)为凹的； 注意到, 点(0,0)是曲线由凸变凹的分界点.
2、拐点的求法
二阶导数等于零的点和二阶导数不存在 的点，可能是拐点．
方法1: (1)
求f ( x)；
(2) 求f ( x) 0及f ( x)不存在的点xi；
(3) 检查xi两近旁f ( x)的符号：
高数 第三节 曲线的凹凸性和函数图形的描绘
y 2 e
(1 2 x 2 )
1
( 1 ,1 e ) 2
1 2
(
1 ,1 e 2 2
1
)
o
x
机动
目录
上页
下页
返回
结束
备用题 求笛卡儿叶形线 x 3 y 3 3a x y 的渐近线 . 解: 令 y = t x , 代入原方程得曲线的参数方程 :
3a t2 3a t , y x t 1 3 3 1 t 1 t 当x 时t 1, 因 y 3a t2 3a t 1 lim lim t 1 1 t 3 x x 3 1 t 3a t2 3a t 3 at (1 t ) lim y ( x) lim lim (1t )(1t t 2 ) 3 3 x t 1 1 t t 1 1 t a 所以笛卡儿叶形线有斜渐近线 y x a
机动
x1x x1 x1x2x2x2 xx x2 x 1 2 2
目录 上页 下页 返回 结束
定义2 . 设函数
在区间 I 上连续 ,
(1) 若曲线弧位于其上每一点处切线的上方， 则称f(x)图形是凹的; (2) 若曲线弧位于其上每一点处切线的下方， y y 则称f(x)图形是凸的 . y 连续曲线上有切线的凹凸分界点
2) 求拐点可疑点坐标
令 y 0 得 x1 0 , x2 2 , 对应 y1 1 , y2 11 3 27 2 3 3) 列表判别
x ( , 0) y y 凹
0 0 1
(0 , 2 ) 3
( 2 , ) 3 0
2 3 11 27
凸
凹
( , 0) 及 ( 2 , ) 上向上凹, 在 (0 , 2 ) 上 故该曲线在 3 3 点 ( 0 , 1 ) 及 ( 2 , 11 ) 均为拐点. 向上凸 , 3 27
曲线的凹凸性与拐点 函数图形的描绘
是拐点，否则就不是．
例2 求曲线 f (x) = x3 - 6x2 + 9x + 1 的凹凸区 间与拐点．
解 (1) 定义域为( , ). (2) f (x) = 3x2 - 12x + 9，f (x) = 6x - 12 = 6(x - 2 )， 令 f (x) = 0，得 x = 2. (3)当 x ( , 2) 时， (x) < 0，此区间为凸区间． f 当 x (2, + ) 时， (x) > 0，此区间是凹区间. f
此时曲线是凹的 .
定义
连续曲线y=f(x)上凹的曲线弧与凸的曲
线弧的分界点，称为曲线 y=f(x)的拐点． 分析：由上述定理可知，通过 f ( x )的符号可 以判断曲线的凹凸. 如果 f ( x )连续，那么当 f ( x )的符号由正变负或由负 变正时，必定有
一点x0，使f x0 0. 这样，点 x0 , f ( x0 )) (
( 2) 如果在(a , b)内，f ( x ) 0，则曲线在 a , b )内 ( 是凸的.
（证明从略）
例1 判断曲线 y=x3 的凹凸性． 解 因为y 3 x 2，y 6 x，所以
当x (, 0)时，y 0，
此时曲线是凸的 ;
当x ( 0, )时，y 0，
数，其图形关于原点对称．
令f (x) = 0，得 x1= -1， x2= 1,
令f (x)=0，得x=0. （3）列表讨论如下：
x f (x) f (x) f (x)
(, 1) + -
1 0 极大值 f (-1)=2
(1, 0) -
0 0 拐点 (0,0)
(0, 1) +
曲线的凹凸性与函数图象描绘省公开课获奖课件说课比赛一等奖课件
f
(2 )( x2
x0 )2 ]
由 f ( x) 0 f ( x1 ) f ( x2 ) 2 f ( x0 ),
即
f
( x1
2
x2
)
1[ 2
f
( x1 )
f
( x2 )]
结论（2）可类似得证. 教材上用langrange定理证明!
例7 判断曲线 y x3 的凹凸性. 解 y 3x2 , y 6x, 当x 0时， y 0,
定理1 如果 f ( x) 在 [a, b] 上连续,在 (a, b)内具有 一阶和二阶导数 ,若在 (a,b)内 (1) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凹的 ; (2) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凸的 .
分析
f ( x1 x2 ) f ( x1 ) f ( x2 ) ,
2
2
不妨设x1
x2 ,令x0
x1
2
x2
,
分别在[ x1 , x0 ]与[ x2 , x0 ]上
f (x)
f ( x0 )
f ( x0 )( x x0 )
1 2!
f ( )( x x0 )2
(在x, x0之间)
定理1 如果 f ( x) 在 [a, b] 上连续,在 (a, b)内具有 一阶和二阶导数 ,若在 (a,b)内 (1) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凹的 ; (2) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凸的 .
凸旳 (2 3 ,1127)
凹旳
凹凸区间为 (,0], [0, 2 3], [2 3 ,).
曲线的凹凸性和拐点、函数图像的描绘
高等数学
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1．曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示，有一类曲线向上弯曲，它在任何点处的切 线总位于曲线的下方；另一类曲线向下弯曲，它在任何点处的 切线总位于曲线的上方，由此我们给出关于曲线凹凸的定义：
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下：
2．函数图像的描绘
（1）确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性（如奇偶性、周期性等）； （2）求出函数的一阶导数 f (x) 和二阶导数 f (x)，解方程
f (x)=0，f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点，应用这些根和点，将函数的定义域划分为若干个子区间； （3）列表讨论 f (x)和 f (x) 在（2）中所得各子区间内的符号，由 此确定函数的单调性、极值、曲线的凹凸性和拐点； （4）如有渐近线，求出渐近线，并确定其他变化趋势； （5）求辅助点，如曲线与坐标轴的交点等； （6）在直角坐标系中，根据上面讨论，描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( ， )
y 4x3 6x2 y 12x2 12x 12x(x 1) ， 令 y 0，得 x 0 和 x 1。 列表讨论如下：
x y
曲线
( ，0) +
0 0 拐点 （0，1）
如果将定理中的区间改为其他区间，结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( ， ) ，y 3x2，y 6x
（当 x 0 时，y 0 ，故曲线在 ( ，0] 内是凸的；当 x 0 时，y 0，股曲线在 [0 ， ) 内是凹的；当x 0时，y 0。 点（0，0）是曲线 y x3由凸变凹的分界点（图3-11）
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1．曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示，有一类曲线向上弯曲，它在任何点处的切 线总位于曲线的下方；另一类曲线向下弯曲，它在任何点处的 切线总位于曲线的上方，由此我们给出关于曲线凹凸的定义：
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下：
2．函数图像的描绘
（1）确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性（如奇偶性、周期性等）； （2）求出函数的一阶导数 f (x) 和二阶导数 f (x)，解方程
f (x)=0，f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点，应用这些根和点，将函数的定义域划分为若干个子区间； （3）列表讨论 f (x)和 f (x) 在（2）中所得各子区间内的符号，由 此确定函数的单调性、极值、曲线的凹凸性和拐点； （4）如有渐近线，求出渐近线，并确定其他变化趋势； （5）求辅助点，如曲线与坐标轴的交点等； （6）在直角坐标系中，根据上面讨论，描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( ， )
y 4x3 6x2 y 12x2 12x 12x(x 1) ， 令 y 0，得 x 0 和 x 1。 列表讨论如下：
x y
曲线
( ，0) +
0 0 拐点 （0，1）
如果将定理中的区间改为其他区间，结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( ， ) ，y 3x2，y 6x
（当 x 0 时，y 0 ，故曲线在 ( ，0] 内是凸的；当 x 0 时，y 0，股曲线在 [0 ， ) 内是凹的；当x 0时，y 0。 点（0，0）是曲线 y x3由凸变凹的分界点（图3-11）
曲线的凹向及函数图形描绘
x1
y
来说，因li为 m 1 0. 所以
x x1
直 线 y0是 曲•线 y
1
o
的水平
x1
渐近线。
yf(x)
1
x
返回
又如 •y曲 ar线 c， tg因 x 为
lia m r c • t• g•x •l• ia • m •r• c •.t ••g ••x
x
返回
例1 讨论 f（ x ） 曲 x 3 线 6x 29x1 的凹 间与拐点.
解 定义 ， 域 ） 为 ， f（ x （ ） 因 3 x 2 为 1x 29，
f ( x ) 6 x 1 6 2 ( x 2 ) 令 f,（ x） 0 ，可 x2.得 当 x （ ， 2）时 f（ x ， ） 0，此区间
返回
例2 讨论曲 y线 ln（ 1x2）的凹凸区间 . 与
解 定义 ， 域 ） .因 为 y 为 1 （ 2 x x 2，
y
2(1 x2 )， (1 x2 )2
令 y 0 ， x 1 得 ， x 1 .
x (,1)
1
f ( x)
x
(1,)
y
y
y
因为
lim ln(x21) ,
x 1
的单调区间 将上述讨论列为下表
x (,1) 1 (1,0) 0
(0,1)
y(x) 0
1 (1,)
0
y(x) y
极小值 2
0
拐点 ( 0 ，0 )
极大值 2
••令 y0 ， 可y 知 3xx 曲 3 与 x 轴 线 交 x3 在
y
来说，因li为 m 1 0. 所以
x x1
直 线 y0是 曲•线 y
1
o
的水平
x1
渐近线。
yf(x)
1
x
返回
又如 •y曲 ar线 c， tg因 x 为
lia m r c • t• g•x •l• ia • m •r• c •.t ••g ••x
x
返回
例1 讨论 f（ x ） 曲 x 3 线 6x 29x1 的凹 间与拐点.
解 定义 ， 域 ） 为 ， f（ x （ ） 因 3 x 2 为 1x 29，
f ( x ) 6 x 1 6 2 ( x 2 ) 令 f,（ x） 0 ，可 x2.得 当 x （ ， 2）时 f（ x ， ） 0，此区间
返回
例2 讨论曲 y线 ln（ 1x2）的凹凸区间 . 与
解 定义 ， 域 ） .因 为 y 为 1 （ 2 x x 2，
y
2(1 x2 )， (1 x2 )2
令 y 0 ， x 1 得 ， x 1 .
x (,1)
1
f ( x)
x
(1,)
y
y
y
因为
lim ln(x21) ,
x 1
的单调区间 将上述讨论列为下表
x (,1) 1 (1,0) 0
(0,1)
y(x) 0
1 (1,)
0
y(x) y
极小值 2
0
拐点 ( 0 ，0 )
极大值 2
••令 y0 ， 可y 知 3xx 曲 3 与 x 轴 线 交 x3 在
曲线的凹凸性与拐点函数图形的描绘
f (x) = 6x - 12 = 6(x - 2 )， 令 f (x) = 0，可得 x = 2.
当 x ( , 2) 时，f (x) < 0，此区间是凸区间． 当 x (2, + ) 时，f (x) > 0， 此区间是凹区间．
当 x = 2 时， f (x) = 0，因 f (x) 在 x = 2 的两 侧变号，而 f (2) = 3， 所以 (2, 3)是该曲线的拐点.
第四模块 微积分学的应用
第六节 曲线的凹凸性与拐点 函数图形的描绘
一、曲线的凹凸性与拐点
二、函数图形的描绘
一、曲线的凹凸性与拐点
y
y
B
D
A C
A
C
B
D
O x1 x2
x3 x4
xO
x1 x2
x3 x4
x
(a)
(b)
如图所示，凡呈凸形的弧段，当自变量 x 由 x1
增大到 x2 时， 其上的切线斜率是递减的(如图(a)左，
x x0
x x0
或 lim x x0
f (x) ,
则称直线
x = x0 为曲线 y = f (x) 的
垂直渐近线.
例如， 对于曲线 y = ln x 来说， 因为
lim ln x ，
y
x0
所以直线 x = 0+ 即 y
轴为 y = ln x 曲线的
O
垂直渐近线.
y = ln x x
又如, 对于曲线 y 1 来说, 因为lim 1 ,
二、函数图形的描绘
1.曲线的水平渐近线和垂直渐近线
定义 3 若曲线 y = f (x) 上 的 动 点 y
M(x, y) 沿着曲线无限
第四节 曲线的凹凸性和函数图形的描绘
列表确定函数升降区间,凹凸区间及极值点和拐点:
x
f ( x ) f ( x )
f (x)
( , 3 ) 3 ( 3 , 2 ) 2
( 2 ,0 )
0
不存在
( 0 , )
0
拐点
( 3, 26 9 )
0
极值点
间 断 点
3
补充点 : ( 1
例3 解
求曲线
y sin x cos x ([ 0 , 2 ]内 ) 的拐点 .
y cos x sin x , y sin x cos x , y cos x sin x .
令 y 0 ,
4
.
2
lim ( x ) lim
x
1 2
x
x
e
2
0,
得水平渐近线
y 0.
列表确定函数升降区间,凹凸区间及极值点与拐点:
x
( x ) ( x )
( x)
( , 1 ) 1
( 1 ,0 )
0 0
( 0 ,1 )
1
( 1 , )
曲线在 [ 0 , ) 上是凸的 .
点 ( 0 , 0 ) 是曲线
y
3
x的拐点 .
二 函数图形的描绘
1.曲线的渐近线
一条曲线在伸向无穷远处的走向是不容易画准确 的，但如果在伸向无穷远时渐渐靠近一条直线，那 么，就可以利用这条直线将曲线的走向画准确了，这 样的直线称为渐近线．
定义２ 若曲线上一点沿曲线远离原点时，该点与某一固定的 直线的距离趋向于零，则称此直线为曲线的渐近线． 渐近线按其走向可分为垂直渐近线、水平渐近线、斜渐 近线三种，本课我们仅对前两种类情形作以介绍． (1)垂直渐近线 与ｙ轴平行的渐近线称为垂直渐近线，如图４－１６所 示．这时，有（或或），则称直线为曲线的垂直渐近 线． 图４－１６ 图４－１７ (2)水平渐近线 与ｘ轴平行的渐近线称为水平渐近线，如图４－１７所 示．这时，有（或或），则称直线为曲线的水平渐近 线．
函数的凹凸性,拐点与图形描绘
0
且f ′( x0 ) = 0, 必有f ′( x ) > 0。 不是极值点。 因此 x = x0 不是极值点。
11
第八节 函数图形的描绘
1.一般步骤 1.一般步骤: 一般步骤: (1) 确定 y = f ( x )的定义域，考察函数的 奇偶性；求出 f ′( x )、 f ′′( x ). 的定义域， 奇偶性； (2) 求出 f ′( x ) = 0 , f ′′( x ) = 0的全部实根 , 及 f ′( x ), f ′′( x )不存在 的点 . 并用这些点把定义域划 分为几个部分区间 . (3) 列表讨论 f ( x )的性质 .
4 没有拐点，且它在（ + 内是凹的。 即 曲线 y = x 没有拐点，且它在（ − ∞， ∞）内是凹的。
9
3 例5 求曲线 y = x 的拐点。 的拐点。 解 定义域：(− ∞ ,+∞ ), 定义域： 1 2 , 当 x ≠ 0 时， y' = 3 2 , y" = − 3 2 3 x 9x x y 当 x = 0 时， ' ， y" 都不存在 。
2 2
用拉格朗日中值定理， 对 f ′( x ) 在 [x0 − θ 2 h, x0 + θ 1h] 用拉格朗日中值定理，得
（1）确定函数 y = f (x)的定义域； 的定义域； 的定义域 找出使 不存在的点x （2）求 f ”(x),找出使 f ”(x)=0 和 f ”(x) 不存在的点 i ； 找出 把定义域划分成为小区间， （3）用xi把定义域划分成为小区间，在每个小区间上判定曲线 的凹凸。 的凹凸。 例1. 判断 y = ln x 的凹凸性 . 1 1 解 定义域 (0， ∞ ), Q y ′ = , y ′′ = − 2 < 0. + x x ∴ 曲线是凸的 .
且f ′( x0 ) = 0, 必有f ′( x ) > 0。 不是极值点。 因此 x = x0 不是极值点。
11
第八节 函数图形的描绘
1.一般步骤 1.一般步骤: 一般步骤: (1) 确定 y = f ( x )的定义域，考察函数的 奇偶性；求出 f ′( x )、 f ′′( x ). 的定义域， 奇偶性； (2) 求出 f ′( x ) = 0 , f ′′( x ) = 0的全部实根 , 及 f ′( x ), f ′′( x )不存在 的点 . 并用这些点把定义域划 分为几个部分区间 . (3) 列表讨论 f ( x )的性质 .
4 没有拐点，且它在（ + 内是凹的。 即 曲线 y = x 没有拐点，且它在（ − ∞， ∞）内是凹的。
9
3 例5 求曲线 y = x 的拐点。 的拐点。 解 定义域：(− ∞ ,+∞ ), 定义域： 1 2 , 当 x ≠ 0 时， y' = 3 2 , y" = − 3 2 3 x 9x x y 当 x = 0 时， ' ， y" 都不存在 。
2 2
用拉格朗日中值定理， 对 f ′( x ) 在 [x0 − θ 2 h, x0 + θ 1h] 用拉格朗日中值定理，得
（1）确定函数 y = f (x)的定义域； 的定义域； 的定义域 找出使 不存在的点x （2）求 f ”(x),找出使 f ”(x)=0 和 f ”(x) 不存在的点 i ； 找出 把定义域划分成为小区间， （3）用xi把定义域划分成为小区间，在每个小区间上判定曲线 的凹凸。 的凹凸。 例1. 判断 y = ln x 的凹凸性 . 1 1 解 定义域 (0， ∞ ), Q y ′ = , y ′′ = − 2 < 0. + x x ∴ 曲线是凸的 .
3.4曲线的凹凸性与函数图形的描绘
课堂练习
2.a, b为何值，点（ 1 ， 3 ）是曲线y ax3 bx2的拐点？ 解 y 3ax2 2bx, y 6ax 2b
6a 2b 0 由(1,3)为拐点得 ; ab 3 3 9 解得a , b . 2 2
课堂练习
3.作出函数y x ln(1 x)的图形。
例如： (0,0)就不是y x 4的拐点.
求曲线凹凸区间及拐点 的步骤 : (1)求出f ( x)的定义域； (2)求出f ( x) 0和f ( x) 不存在的点; (3)列表考察上述各点相邻 两侧f ( x)符号.( 异号拐点 )
3.4 曲线的凹凸性与函数图形的描绘
例3.4.2 求曲线y
y
y f1 ( x)
B
A
O
y f 2 ( x)
x
3.4 曲线的凹凸性与函数图形的描绘
等价描述：
设f ( x)在区间I上连续 , 如果对I上任意两点x1 , x2 , 恒有 x1 x2 y f ( x1 ) f ( x2 ) f( ) f ( x1 ) f ( x2 ) 2 2 2 那么称f ( x)在I上的图像是向上凹的； 如果恒有
作图的一般步骤如下： （ 1 ）确定函数的定义区间 ； （ 2 ）考查函数的奇偶性、 周 期性与有界性； （ 3 ）确定函数的单调区间 和 极值点，凹凸区间与拐 点； （ 4 ）求曲线的渐进线； （ 5 ）借助辅助点，描出函 数的图像.
x 1 y x2
y
3
水平渐进线
垂 直 渐 近 线
2 1 1 1 2 3
x1 x2 2
x2
x
O
x1
x2
x
3.4 曲线的凹凸性与函数图形的描绘
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y弦
f
(x1)
f
(
x2 ) x2
f( x1
x1
)
(
x
x1
)
x x1 (1 ) x2 , (0, 1)
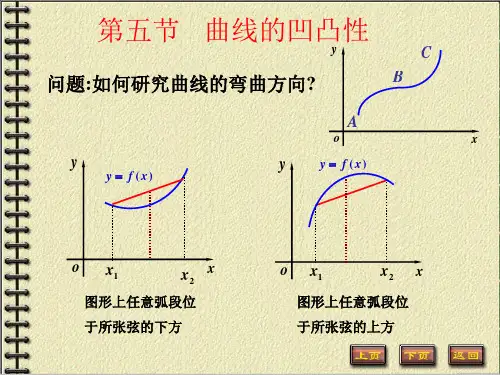
曲线位于弦线下方 : f (x) y弦
即 f ( x1 (1 )x2 ) f (x1) (1 ) f (x2 )
1. 曲线凹凸性的定义及其判别法
设 f (x) C( I ) , (0, 1) .
f
(x2 ) x2
f (x1) (x x1
x1 )
x x1 (1 ) x2 , (0, 1)
曲线位于弦线上方 : f (x) y弦
即 f ( x1 (1 )x2 ) f (x1) (1 ) f (x2 )
y
凹
Q
y f (x)
P
O a x1 x
x2 b
x
弦线 PQ 的方程: 点 x 的坐标 :
x a2 时 , y 0 , 3a1
x a2 时 , y 0 , 3a1
曲线在 ( a2 , ) 中是凹的; 3a1
曲线在 ( , a2 ) 中是凸的; 3 a1
x a2 是曲线凹凸性的分界点. 3a1
例3 解
研究 y x4 在 (1, 1)内的凹凸性. y 4x3, y 12x2 ,
y
y g(x)
•
O
x
O
x
定理 ( 判别拐点的必要条件 )
设 f (x) 在区间 I 上二阶可导. 若 (x0, y0 ) 为曲线 y f (x) 的拐点(x0 I ) , 则 f (x0 ) 0 .
定理 ( 判别拐点的充分条件 )
空心邻域
0
设 f (x) C( I ) , f (x) 在 N (x0 ) (x0 I ) 内二阶可导.
若 f (x) 在点 x0 两侧符号相反, 则
点(x0, f (x0 )) 为曲线 y f (x) 的拐点.
定理 ( 判别拐点的充分条件 )
设 f (x) C( I ) , f (x) 在 U(x0 ) (x0 I )内三阶可导.
若 f (x0 ) 0 , 且 f (x0 ) 0 , 则点(x0, f (x0 )) 为曲线 y f (x) 的拐点.
2
b
y
,
由拐点的必要条件得: y1 0 . 以 x 2 , y 2.5 代入得:
60 8 a 5b 0 (1)
又拐点在曲线上, 其坐标满足曲线方程, 得 :
10 2 a 2.5b 0 (2)
联立(1) , (2) 成方程组, 解之得
a 20 , 3
b 4. 3
函数的凹凸性的判别 以及函数的极值的判别都 与函数的二阶导数有关.
x x
x
有一条斜渐近线 y a x b .
例7 解
求曲线 y x2 1的渐近线. x
lim x2 1 x x
曲线无水平渐近线
lim x2 1 , lim x2 1
x x 0
x x 0
曲线有垂直渐近线 x 0.
x2 1
lim
x
x x
lim
x
x
2 1 x2
1
a 1
( ) ( ) lim x2 11 x lim 1 0
成立 , 则称曲线 y f (x) 在区间 I 上是凹的 ;
定理 设 f (x) C( [a, b] ) , 在 (a, b)内有二阶导数.
若 f (x) 0 , x (a, b) , 则曲线 y f (x) 在[a, b] 上是凹的. 若 f (x) 0 , x (a, b) , 则曲线 y f (x) 在[a, b] 上是凸的.
x (1, 1)时, y 0 , 且仅在 x 0时 , y 0 ,
故 y x4 在 (1, 1)内是凹的.
y
y x4
O
x
x 0 只是使 y 0 的孤立点, 不是曲线凹凸性 的分界点.
2. 曲线拐点的定义及判别法
连续曲线上凸弧与凹弧度分界点 , 称为曲线的拐点.
y
y f (x)
•• •
曲
水平渐近线
线
的 渐
垂直渐近线
近
线
斜渐近线
水平渐近线
若 lim f (x) b , 则曲线 f (x) 有一条水平渐近线 y b . x
这里的极限可以是 lim f (x) b 或 lim f (x) b .
x
x
垂直渐近线
若 lim f (x) , 则曲线 y f (x) 有一条垂直渐近线 x a . xa
曲线的凹凸性、 函数图形的描绘
一、曲线的凹凸性、拐点 二、曲线的渐近线
三、函数图形的描绘
一、曲线的凹凸性、拐点
我们说一个函数单调增加, 你能画出函数
所对应的曲线的图形吗?
y
.B
?!
.A
O
x
y y f (x)
凸
Q
P
O a x1 x
x2 b
x
弦线 PQ 的方程: 点 x 的坐标 :
y弦
f
(x1)
y
0
0
y
0
y
极
拐
大
点
极大点: x 5 , 极大值: f (5) 13.5 ,
拐点为 (1, 0) .
lim
x
(x 1)3 (x 1)2
,
曲线无水平渐近线 .
lim
x1
( (
x x
1)3 1)2
,
x 1为垂直渐近线 .
lim
x
f
(x) x
lim
x
(x 1)3 x (x 1)2
1
a 1
lim(
a 1
lim( y (1) x)
x
lim
t 1
t
2
3k t
t
1
k
b k
故曲线有斜渐近线 y x k .
现在给定一个函数 , 我们可以讨论它的：
定义域、 值 域、 奇偶性、 有界性、 周期性、 连续性、 间断点、 可微性、 单调性、 极 值、 最 值、 凹凸性、 拐 点、 渐近线、 零点位置 . 用极限讨论函数的变化趋势 . 用泰勒公式将函数离散化 .
在 (1,
1) 内为凸的.
点 (1,
e
1 2
)
及
(
1,
e
1 2
)
为其拐点.
例5
证明:
x
y时,
1 (ex
x y
ey) e 2 .
2
解 令 f (t) et , t ( , ) ,
f (t) f (t) et 0 , t ( , ) ,
故 f (t) et 所对应的曲线在( , )内是凹的.
例4 解
讨论曲线 y
x2
e2
的凹凸性,
并求拐点.
定义域为:
( , )
x2
y xe 2 ,
y
(x2
x2
1)e 2
,
令 y 0 得拐点可疑点: x 1, x 1 (横坐标)
x ( , 1) 1 (1, 1) 1 (1, )
y
0
0
y
拐点 拐点
曲线
y
e
x2
2在:
(
,
1)
及
( 1,
) 内为凹的,
求拐点一般步骤
求曲线 y f (x) 拐点的一般步骤 : (1) 求 f (x) 的定义域(或确定讨论区间) ; (2) 计算 f (x) , f (x) , (如需要可求出f (x)) ; (3) 求拐点可疑点:使 f (x) 0的点和 f (x) 不存在的点; (4) 根据定理判别可疑点是否确为拐点.
y
(x 1)3 (x 1)2
的图形 .
函数的定义域 : x (, 1) (1, ) .
y
(
x
1)2 (x (x 1)3
5)
,
y
24(x 1) (x 1)4
,
令 y 0 , 得驻点 x 1, x 5 ,
令 y 0 , 得拐点可疑点 x 1,
x (, 5) 5 (5, 1) 1 (1, 1) 1 (1, )
x
f
(
x)
a
x)
lim
x
5
x2 (x
2 1)
x
2
1
5
曲线有斜渐近线 y x 5.
此外, 曲线与y 轴相交于点(0, 1) .
b 5
y
y
(x (x
1)3 1) 2
(1, 0)
•
5 1 O
x
y x5
13.5
三、函数图形的描绘
作函数图形的一般步骤如下： (1) 确定函数的定义域 , 观察奇偶性、周期性 . (2) 求函数的一、二阶导数 , 确定极值可疑点和拐点可疑点 . (3) 列表 , 确定函数的单调性、凹凸性、极值、拐点 . (4) 求曲线的渐近线 . (5) 作出函数的图形 .
例9 解
作出函数
你清楚它们之间的联系吗? 画画图就能搞清楚.
凸 极大 f (x) 0
凹 极小 f (x) 0
二、曲线的渐近线
若动点 P 沿着曲线 y = f ( x ) 的某一方向无
定义 限远离坐标原点时, 动点 P 到一直线 L 的距离
趋于零 , 则称此直线 L 为曲线 y = f ( x ) 的一条 渐近线 .
x (0, ) 时 , y 0 , y 1 为凹的 . x
该函数的图形 请自己绘出.
例2
研究 y a1x3 a2 x2 a3x a4 (a1 0) 的凹凸性 .
解
函数的定义域为 ( , ) .