高数函数图形的描绘

函数图形的描绘在中学时我们用描点法来作函数的图像，这种方法常遗漏曲线的一些关键点，如极值点、拐点等，使得函数的一些重要性态难以准确地显示出来。

在本章前两节我们借助于导数的符号讨论了函数图形的升降和凹凸，以及在什么地方有极值点，什么地方有拐点，这样也就基本掌握了函数的性态，并把函数的图形画得比较准确。

此外，为了描绘函数图形在无穷远处的走势，还有必要讨论函数图形在无穷远处的变化趋势，即渐近线。

一、渐近线1、定义定义 若曲线)(x f y =上一动点沿着曲线无限远去时，该点与某条定直线L 的距离趋于零，则称直线L 为曲线)(x f y =的渐近线（如图153--）。

2、分类渐近线可分为水平渐近线、铅直渐近线和斜渐近线。

（1）水平渐近线 若函数)(x f y =的定义域为无穷区间，且C x f x =∞→)(lim （或C x f x x =-∞→+∞→)(lim )(） 图153--则称直线C y =为曲线)(x f y =的水平渐近线。

例如，因为01lim=∞→x x ，故直线0=y 为曲线xy 1=的水平渐近线；又如，因为2arctan lim π=+∞→x x ，2arctan lim π-=-∞→x x ，故直线2π=y 及直线2π-=y 均为曲线x y arctan =的水平渐近线。

（2）铅直渐近线 若函数)(x f y =在点0x 处间断，且∞=→)(lim 0x f x x则称直线0x x =为曲线)(x f y =的铅直渐近线。

注：铅直渐近线定义式∞=→)(lim 0x f x x 中，0x x →可换作-→0x x 或+→0x x ，∞→)(x f 亦可换作-∞→)(x f 或+∞→)(x f 。

例如，因为∞=→x x 1lim0，故直线0=x 为曲线xy 1=的铅直渐近线；又如，因为-∞=+→x x ln lim 0，故直线0=x 为曲线x y ln =的铅直渐近线。

*（3）斜渐近线 设有函数)(x f y =，若0)]()([lim =+-∞→b ax x f x则称直线b ax y +=为曲线)(x f y =的斜渐近线，其中xx f a x )(lim∞→=，])([lim ax x f b x -=∞→注：若x x f x )(lim ∞→不存在，或虽然xx f x )(lim ∞→存在但])([lim ax x f x -∞→不存在，则可以断定)(x f y =不存在斜渐近线。

高等数学入门——描绘函数图像的一般步骤及例子高等数学是大学数学的基础课程之一，其重要内容之一是描绘函数的图像。

描绘函数图像的一般步骤如下：1.确定定义域和函数的类型：首先需要确定函数的定义域，即函数可以取值的范围。

同时，需要确定函数是一元函数还是多元函数，是线性函数还是非线性函数等。

2.求导或求导数的一般规律：对于一元函数，可以通过求导的方法来描绘函数的变化趋势。

求导可以确定函数的关键点，如极值点、拐点等。

对于多元函数，则需要利用偏导数来确定函数的变化趋势。

3.确定增减、凹凸和拐点：通过求导或偏导数，可以确定函数的单调性和凹凸性。

当导数为正时，函数单调递增；当导数为负时，函数单调递减。

当二阶导数大于零时，函数凹，小于零时函数凸。

4.确定函数的特殊点：特殊点包括与坐标轴的交点、零点、无穷大点等。

这些点是函数图像的关键部分，需要特别关注。

5.确定函数的渐近线：渐近线是函数图像在无穷远点的变化趋势。

有水平渐近线、垂直渐近线和斜渐近线等。

下面举例说明：例子1：绘制函数y=x^2-2x+1首先，确定定义域和函数的类型：该函数为一元二次函数，定义域为实数集。

然后，求导：y'=2x-2接着，确定增减、凹凸和拐点：当x<1时，y'<0，函数递减；当x>1时，y'>0，函数递增；令y'=0，则x=1，该点为拐点。

继续求二阶导数：y''=2可以确定函数为凹函数。

然后，确定函数的特殊点：与x轴的交点为y=0，即x=1；与y轴的交点为x=0。

最后，确定函数的渐近线：无垂直渐近线；当x趋于无穷大时，y趋于无穷大，可以确定y轴为水平渐近线。

综上所述，根据以上步骤，我们可以描绘出函数y=x^2-2x+1的图像。

例子2：绘制函数 y = sin(x) / x首先，确定定义域和函数的类型：该函数为一元函数，定义域为实数集，但要注意x≠0。

然后，求导：y' = (x*cos(x) - sin(x)) / x^2接着，确定增减、凹凸和拐点：当x<0时，y'>0，函数递增；当x>0时，y'<0，函数递减；令 y' = 0，则 x = tan(x)，求解该方程需要使用数值逼近法得到近似解。

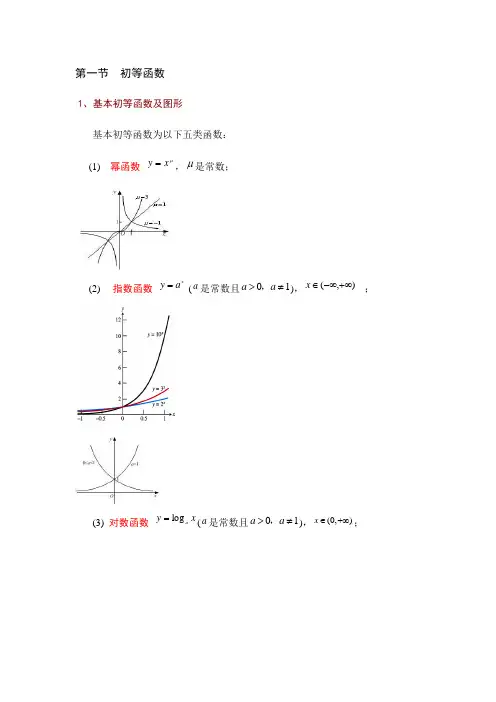
第一节 初等函数1、基本初等函数及图形基本初等函数为以下五类函数：(1) 幂函数 μx y =，μ是常数；(2) 指数函数 x a y = (a 是常数且01a a >≠，)，),(+∞-∞∈x ；(3) 对数函数 x y a log =(a 是常数且01a a >≠，)，(0,)x ∈+∞；(4) 三角函数正弦函数 x y sin =，),(+∞-∞∈x ，]1,1[-∈y ，余弦函数 x y cos =，),(+∞-∞∈x ，]1,1[-∈y ，正切函数 x y tan =，2ππ+≠k x ，k Z ∈，),(+∞-∞∈y ，余切函数 x y cot =，πk x ≠，k Z ∈，),(+∞-∞∈y ；(5) 反三角函数反正弦函数 x y arcsin =， ]1,1[-∈x ，]2,2[ππ-∈y ，反余弦函数 x y arccos =，]1,1[-∈x ，],0[π∈y ，反正切函数 x y arctan =，),(+∞-∞∈x ，)2,2(ππ-∈y ，反余切函数 x y cot arc =，),(+∞-∞∈x ，),0(π∈y ．我现在就付诸行动［美］奥格.曼狄诺著安辽我的幻想毫无价值，我的计划渺如尘埃，我的目标不可能达到。

一切的一切毫无意义——除非我们付诸行动。

我现在就付诸行动。

一张地图，不论多么详尽，比例多么精确，它永远不可能带着它的主人在地面上移动半步。

一个国家的法律，不论多么公正，永远不可能防止罪恶的发生。

任何宝典，即使我手中的羊皮卷，永远不可能创造财富。

只有行动才能使地图、法律、宝典、梦想、计划、目标具有现实意义。

行动像食物和水一样，能滋润我，使我成功。

我现在就付诸行动。

拖延使我裹足不前，它来自恐惧。

现在我从所有勇敢的心灵深处，体会到这一秘密。

我知道，要想克服恐惧，必须毫不犹豫，起而行动，惟其如此，心中的慌乱方得以平定。

现在我知道，行动会使猛狮般的恐惧减缓为蚂蚁般的平静。

高中数学函数图像大全1. 常用数学函数1.1. 直线函数直线函数是数学中最简单的函数之一。

它的特点是图像为一条直线，表达式为y=kx+b，其中k和b是常数。

直线函数的图像与直线的斜率和截距有关。

1.2. 平方函数平方函数的图像为抛物线，表达式为y=x2。

平方函数的特点是对称于y轴，并且开口向上。

1.3. 立方函数立方函数的图像为一条类似于S字形的曲线，表达式为y=x3。

立方函数的特点是对称于原点，并且开口向上。

1.4. 平方根函数平方根函数的图像为一条向右开口的抛物线，表达式为 $y = \\sqrt{x}$。

平方根函数的特点是定义域为非负实数集。

1.5. 绝对值函数绝对值函数的图像为一条折线，表达式为y=|x|。

绝对值函数的特点是对称于y轴，并且在原点处转折。

2. 复合函数复合函数是由两个或多个函数相互组合而成的函数。

其图像可以通过将各个函数的图像进行组合来得到。

3. 反函数反函数是与给定函数互为反函数的函数。

其图像可以通过将给定函数的图像关于直线y=x进行对称得到。

4. 常见函数图像的变换常见函数图像可以通过平移、伸缩、翻转等操作进行变换，从而得到新的函数图像。

4.1. 平移变换平移变换是将函数图像沿x轴或y轴方向移动的操作。

对于函数y=f(x)，平移变换的一般形式为y=f(x−a)或y=f(x)+b。

4.2. 伸缩变换伸缩变换是将函数图像在水平或垂直方向进行拉伸或压缩的操作。

对于函数y=f(x)，伸缩变换的一般形式为 $y = a \\cdot f(bx)$。

4.3. 翻转变换翻转变换是将函数图像关于x轴或y轴进行翻转的操作。

对于函数y=f(x)，翻转变换的一般形式为y=−f(x)或y=f(−x)。

5. 实际应用数学函数图像在实际应用中起到了重要的作用。

例如，在物理学中，函数图像可以用来描述物体的运动轨迹；在经济学中，函数图像可以用来描述经济变量之间的关系；在计算机科学中，函数图像可以用来进行数据的可视化等。