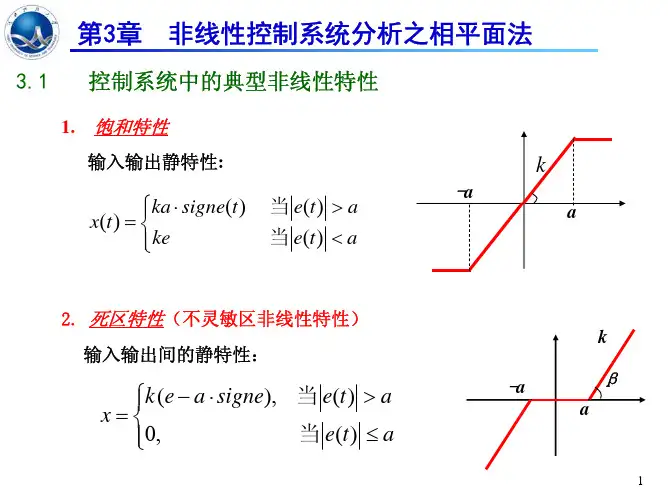
相平面法
- 格式：ppt
- 大小：1015.50 KB
- 文档页数：41
文档推荐
-
相平面页数:40
-
非线性系统的分析_相平面1页数:64
-
实验十一：非线性系统的相平面分析页数:4
-
非线性系统的分析相平面优秀课件页数:64
-
7-2相平面法页数:25
-
相平面分析资料页数:26
-
相平面分析页数:23
下载文档原格式
合集下载
相平面法
1 的情况相同，只是 运动方向相反。
<3>正反馈二阶系统：
n2 x 0 x 2 n x
s 1 .2 n n 2 1
则 s 1 0 , 而 s 2 0。
相轨迹存在的两条特殊的等 倾线也是相轨迹，其斜率分
k 1 s 1 , k 2 s 2，同时它 别为：
初条下的运动对应多条相轨迹，形成相轨迹簇。而
由一簇相轨迹所组成的图形——相平面图。 二、相轨迹的绘制： （1）解析法、（2）作图法、（3）实验法 （一）解析法：求出相轨迹的解，再画出相轨迹。
相轨迹的绘制（续）
适用场合：（1）运动方程比较简单 （2）可以分段线性化 例1、如图所示，弹簧—质量运动系统， m 为物体质 量，k 为弹性系数。 若初条为
2 n x dx dx x
dx n2 x d x 则 有x
2 x 2 x 2 A2 n
其中A是初条决定的积分常数，此为同心椭圆。
2、 0 1:
由第三章知： x ( t ) A e n t s in( d t ), d n 1
由x— 2、相轨迹
组成的直角坐标平面——相平面。 x
0 )起 ， 相变量从初始时刻 t0 对应的状态点 ( x 0， x
随着时间的推移，在相平面上运动形成 的曲线
基本概念（续）
——相轨迹。
3、相平面图： 根据微分方程解的存在和唯一性定理，对于任一给 定的初条，相平面上有一条相轨迹与之对应，多个
由初始条件求得。
相轨迹的绘制（续）
可见：直线c=r[在此r=1]
将相平面分成两个
区域I和II。 1）若初始条件处于A点(II内):
非线性系统的分析_相平面1
) 控制系统的任一动态过程可由状态变量 ( x , x 来表示。
为横轴和纵轴构成的坐标平 1.相平面:以x 和 x 面.
2.相点:相平面上任一点
) ( x, x
3.相轨迹: 对二阶系统来讲，从某一初始状态出发， 以时间t为参变量，便可画出一条连续变化的相轨迹。
x
M1
x
M
2
4.相轨迹特点: ⑴与初始点(状态)密切相关. ⑵可以不直接求出微分方程而获得系统所有 运动状态. 5.相轨迹判断系统稳定性
●
设
系统微分方程为
特征根为两个不相等的正实根，系统不稳定， 过渡过程为非周期发散。等倾线方程为
●
系统特征根为两个相同的正实根，存在一条特殊的 等倾线，系统相轨迹发散，相平面图如下图所示。
四．非线性系统的相平面分析
一般非线性系统利用分段线性微分方程来描述。 1）分段列写非线性系统微分方程
2）在相平面上确定每一个微分方程所在区域 及开关线。 3）按照线性系统相轨迹的作法，分段求解相 轨迹方程。 4）在开关线上做好两条相轨迹的链接。注意， 下一条相轨迹的初始条件是上一条相轨迹的终 止条件。
根据 的选取，可以分为以下几种情况：
●
设
系统微分方程为
特征根为两个具有负实部的共轭复根，系统 稳定，过渡过程呈衰减震荡形式。 其等倾线方程为
ห้องสมุดไป่ตู้
●
特征根为两个不相等的负实根，
系统的零输入响应为非震荡衰减形式，存在两条 特殊的等倾线，其斜率为
相平面图如下图所示。当相轨迹初始点落在两条特 殊等倾线上时，相轨迹沿该直线趋于原点；除此之 外，相轨迹最终将沿着 的方向趋于原 点。
i.等斜线方程:
i.等斜线分布图. 1 1 .2 1 .1 ii.相轨迹 A点 a1 1 过点 A, a1
为横轴和纵轴构成的坐标平 1.相平面:以x 和 x 面.
2.相点:相平面上任一点
) ( x, x
3.相轨迹: 对二阶系统来讲，从某一初始状态出发， 以时间t为参变量，便可画出一条连续变化的相轨迹。
x
M1
x
M
2
4.相轨迹特点: ⑴与初始点(状态)密切相关. ⑵可以不直接求出微分方程而获得系统所有 运动状态. 5.相轨迹判断系统稳定性
●
设
系统微分方程为
特征根为两个不相等的正实根，系统不稳定， 过渡过程为非周期发散。等倾线方程为
●
系统特征根为两个相同的正实根，存在一条特殊的 等倾线，系统相轨迹发散，相平面图如下图所示。
四．非线性系统的相平面分析
一般非线性系统利用分段线性微分方程来描述。 1）分段列写非线性系统微分方程
2）在相平面上确定每一个微分方程所在区域 及开关线。 3）按照线性系统相轨迹的作法，分段求解相 轨迹方程。 4）在开关线上做好两条相轨迹的链接。注意， 下一条相轨迹的初始条件是上一条相轨迹的终 止条件。
根据 的选取，可以分为以下几种情况：
●
设
系统微分方程为
特征根为两个具有负实部的共轭复根，系统 稳定，过渡过程呈衰减震荡形式。 其等倾线方程为
ห้องสมุดไป่ตู้
●
特征根为两个不相等的负实根，
系统的零输入响应为非震荡衰减形式，存在两条 特殊的等倾线，其斜率为
相平面图如下图所示。当相轨迹初始点落在两条特 殊等倾线上时，相轨迹沿该直线趋于原点；除此之 外，相轨迹最终将沿着 的方向趋于原 点。
i.等斜线方程:
i.等斜线分布图. 1 1 .2 1 .1 ii.相轨迹 A点 a1 1 过点 A, a1
相平面法
7-4 相 轨 迹一、相轨迹的概念设二阶系统可以用下列常微分方程描述),(x x f x= 或),(xx f dtxd = 式中),(xx f 一般是x 和x 的非线性函数。
该系统的时域解，可以用x 与t 的关系曲线来表示。
也可把时间t 作为参变量，用x 与x之间的关系曲线来表示。
下面以线性二阶系统为例加以说明。
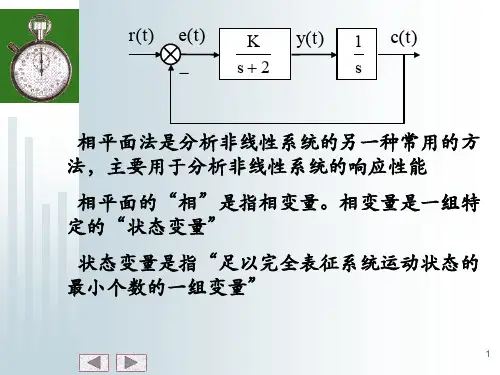
设线性二阶系统如图7-34(a)所示，其单位阶跃响应及其导数如图7-34(b)所示。
即可把系统的阶跃响应用图7-34(c)所示的x 与x 之间的关系曲线来描述，由图可见，xx -曲线同样很直观地表示了系统的运动特性。
从某种意义上来说，甚至比)(t x 曲线更形象，可获得更多的信息。
显然，如果把方程),(x x f x=看作是一个质点运动方程，用x 表示质点的位置，那么x 就表示质点的运动速度。
用x 和x 描述方程的解，也就是用质点的“状态”（位置和速度）来表示该质点的运动。
在物理学中，这种不直接用时间变量而用状态变量来描述运动的方法称为相空间方法，也称为状态空间法。
在自动控制理论中，把具有直角坐标xx -的平面称为相平面。
相平面是二维的状态空间（平面），相平面上的每个点对应着系统的一个运动状态，这个点就称为相点。
相点随时间t 的变化在xx -平面上描绘出的轨迹线，表征了系统运动状态（相）的演变过程，这种轨迹称为相轨迹。
对于二阶系统，它的状态变量只有两个，所以二阶系统的运动可在相平面上表示出来。
对于三阶系统，它有三个状态变量，必须用三维空间来描述其相迹，这就比较困难了。
对于三阶以上的系统，要作其相轨迹就更加困难；然而原则上可以将二维空间中表示点运动的概念扩展到n 维空间去。
相平面法是一种用图解求下列两个联立一阶微分方程组的方法。
首先把二阶常微分运动方程),(x x f x= 改写成两个联立一阶微分方程，令1x x =，21x x =∙则有12212(,)dx x dt dx f x x dt ⎧=⎪⎪⎨⎪=⎪⎩ 或 (,)dxx dtdx f x x dt⎧=⎪⎪⎨⎪=⎪⎩ （7-20）用（7-20）式的第一个方程除第二个方程，可得xx x f dx xd ),(1= （7-21）解（7-21）式就可得相轨迹方程，作出相迹来。
现代控制理论补充内容(2)——相平面法
增量式简化为 ： x =
∂f ( x, x) ∂x
x = x0 x + x = x0
∂f ( x, x) ∂x
x = x0 x = x0
x
20
本例， x + 0.5 x + 2 x + x 2 = 0
f ( x, x) = −(0.5 x + 2 x + x 2 )
⎧x = 0 令： ⎨ ⎩ f ( x, x ) = 0
鞍点ζ=0
2 x − ω0 x = 0
或 b=0, S=0,s=-a
17
3.5
相平面图中的奇点和奇线
x dx f ( x, x ) 0 = = 的点。 (1) 奇点： 亦即满足： = x dx x 0
根据奇点附近的相轨迹变化的不同，奇点可分为： 稳定焦点、不稳定焦点、稳定节点、不稳定节点、中心点和鞍点。
12
具体做法： 从初始点开始，依次求圆心位置：
δ1 =
f ( x1 , x1 , t1 ) + ω 2 x1
ω2
画出一系列圆弧，连接成线，即为系统的相轨迹图。
13
3.4
线性系统的相轨迹
1 线性一阶系统的相轨迹
一阶系统的描述方程：
Tc + c = 0
相轨迹方程：
1 c=− c T
——过原点的直线方程
x1 , x1 , t 都很小，可认为 δ ( x, x, t ) = δ1为常量， f ( x1 , x1 , t1 ) + ω 2 x1 其中， δ1 = 2
于是，系统方程可写为：x + ω
ω
2
x = ω 2δ1
x + ω 2 ( x − δ1 ) = 0
《自动控制原理》 相平面法
(8-24) (8-25) (8-26) (8-27)
c(t) = − b c(t) = kc(t)
+a
(8-28)
其中k为等倾线的斜率。当 a2 − 4b 0时，且 b 0 时，可得满
足k＝a的两条特殊的等倾线，其斜率为: ???
k1,2 = 1,2 = s1,2 = − a
a2 2
− 4b
(2)线性二阶系统的相轨迹
c + ac + bc = 0
当b>0时，上述(运动)微分方程又可以表示为
c + 2wnc + wn2c = 0
线性二阶系统的特征根
s1,2 = − a
a2 − 4b 2
相轨迹微分方程为 (相轨迹切线斜率ZX)
dc dc
=
−
ac − c
bc
令
−
ac − bc c
=
，可得等倾线方程为：
初始条件下的运动对应多条相轨迹，形成相轨迹簇，而由一簇相轨
迹所组成的图形称为相平面图。
若已知x和 x 的时间响应曲线如图8-10(b),(c)所示，则可根据 任一时间点的x(t)和 x(t)的值，得到相轨迹上对应的点，并由此获
得一条相轨迹，如图8—10(a)所示。
相轨迹在某些特定情况下，也可以通过积分法，直接由微分方
U+jV 表示根为复数
2
2.00
2
7.46
s2 // jV -2.41 -2.00 0.00 -2.24 -7.46 -3.00 -2.00 -2.24 2.00 0.54
1)b<0。系统特征根
− a + a2 + 4b
s1 =
2
第七章相平面法2010
7.6 相平面法
一、相平面的基本概念 二、相轨迹的绘制 三、由相轨迹求系统的瞬态响应 四、奇点与极限环 五、非线性系统的相平面分析
1
一、相轨迹的基本概念
解决两个问题： 1.什么是相轨迹？ 2.相轨迹的几个重要性质。
2
（一）相轨迹的基本概念
相平面法是状态空间法在二维空间特殊情况下的应用。 它是一种通过图解法求解一阶或二阶线性或非线性系统的 准确方法。它可以给出某一平衡状态稳定性的信息和系统 运动的直观图像。所以，它属于时间域的分析方法。
12
等倾线与相轨迹
x n2 x 2n
设系统参数 ξ=0.5，ω＝1。求得 对应于不同α 值的等 倾线
x
－ 1.2 － 1.4
k＝ － 1
A
B
－ 1.6 － 1.8 －2
C D
－ 2.5 －3
0
－ 1.4 － 1.2
－ 0.8－ 0.6－ 0.4－ 0.20
1 0.5
－4 －6
对于二阶时不变系统，可用以下常微分方程来描述：
x f (x, x) 0
设: x1 x x2 x
x1 x x2 则: x2 x f (x1 , x2 )
3
相平面、相轨迹、相平面图
x
定义：
X
(t
)
x1 x2
为状态变量。
0
x
我们将 (x , x ) 构成的直角平面叫做相平面。
－ 11 x
9 4 2
13
用等倾线法相轨迹绘制
14
三、由相轨迹求系统的瞬态响应
相轨迹是消去时间后画出的，尽管它直观地给出了系 统状态的运动轨迹，但却将时间信息隐含其中，使时间信 息变得不直观了。有时我们希望给出时间响应以便得到与 时间有关的性能指标，这就需通过相轨迹求出时间信息。
一、相平面的基本概念 二、相轨迹的绘制 三、由相轨迹求系统的瞬态响应 四、奇点与极限环 五、非线性系统的相平面分析
1
一、相轨迹的基本概念
解决两个问题： 1.什么是相轨迹？ 2.相轨迹的几个重要性质。
2
（一）相轨迹的基本概念
相平面法是状态空间法在二维空间特殊情况下的应用。 它是一种通过图解法求解一阶或二阶线性或非线性系统的 准确方法。它可以给出某一平衡状态稳定性的信息和系统 运动的直观图像。所以，它属于时间域的分析方法。
12
等倾线与相轨迹
x n2 x 2n
设系统参数 ξ=0.5，ω＝1。求得 对应于不同α 值的等 倾线
x
－ 1.2 － 1.4
k＝ － 1
A
B
－ 1.6 － 1.8 －2
C D
－ 2.5 －3
0
－ 1.4 － 1.2
－ 0.8－ 0.6－ 0.4－ 0.20
1 0.5
－4 －6
对于二阶时不变系统，可用以下常微分方程来描述：
x f (x, x) 0
设: x1 x x2 x
x1 x x2 则: x2 x f (x1 , x2 )
3
相平面、相轨迹、相平面图
x
定义：
X
(t
)
x1 x2
为状态变量。
0
x
我们将 (x , x ) 构成的直角平面叫做相平面。
－ 11 x
9 4 2
13
用等倾线法相轨迹绘制
14
三、由相轨迹求系统的瞬态响应
相轨迹是消去时间后画出的，尽管它直观地给出了系 统状态的运动轨迹，但却将时间信息隐含其中，使时间信 息变得不直观了。有时我们希望给出时间响应以便得到与 时间有关的性能指标，这就需通过相轨迹求出时间信息。
7-2相平面法
bx cx 0 x
当c > 0时，上述微分方程又可以表示为
2 2 n x n x 0 x
线性二阶系统的特征根
b b 4c s1 2
2
b b 2 4c s2 2
相轨迹方程为
dx bx cx dx x
假设由初始条件确定的点为图中的A点。则过A点作斜率为[ (1) + (1.2) ] / 2 = 1.1的直线，与a = 1.2的等倾线交于B点。再过B 点作斜率为的[ (1.2 ) + (1.4) ] / 2 = 1.3 直线，与a = 1.4的等 倾线交于C点。如此依次作出各等倾线间的相轨迹线段，最后即 得系统近似的相轨迹。
x t4
(x, x0)
t3
0 t2 0
t1
x
x
t1
t2 t3 t4
4
当t变化时，系统状态在相 平面上移动的轨迹称为相轨迹。
t
而与不同初始状态对应的一簇相轨迹所组成的图 叫做相平面图。 利用相平面图分析系统性能的方法称为相平面法。
7.3.2 相平面图的绘制
绘制相平面图可以用解析法、图解法和实验法。 1. 解析法 解析方法一般用于系统的微分方程比较简单或可 以分段线性化的方程。应用解析法求取相轨迹方程时 一般有二种方法：一种是对式（7-35）直接进行积分。 显然，这只有在上述方程可以进行积分时才能运用。 另一种方法是先求出x和对t的函数关系，然后消去t， 5 从而求得相轨迹方程。下面举例加以说明。
x
0
x
22
④ = 0。系统特征根为一对纯虚根。系统的自 由运动为等幅正弦振荡。给定初始点，系统的相平 面图为围绕坐标原点的一簇椭圆（参阅例7-1），系 统相平面图:
当c > 0时，上述微分方程又可以表示为
2 2 n x n x 0 x
线性二阶系统的特征根
b b 4c s1 2
2
b b 2 4c s2 2
相轨迹方程为
dx bx cx dx x
假设由初始条件确定的点为图中的A点。则过A点作斜率为[ (1) + (1.2) ] / 2 = 1.1的直线，与a = 1.2的等倾线交于B点。再过B 点作斜率为的[ (1.2 ) + (1.4) ] / 2 = 1.3 直线，与a = 1.4的等 倾线交于C点。如此依次作出各等倾线间的相轨迹线段，最后即 得系统近似的相轨迹。
x t4
(x, x0)
t3
0 t2 0
t1
x
x
t1
t2 t3 t4
4
当t变化时，系统状态在相 平面上移动的轨迹称为相轨迹。
t
而与不同初始状态对应的一簇相轨迹所组成的图 叫做相平面图。 利用相平面图分析系统性能的方法称为相平面法。
7.3.2 相平面图的绘制
绘制相平面图可以用解析法、图解法和实验法。 1. 解析法 解析方法一般用于系统的微分方程比较简单或可 以分段线性化的方程。应用解析法求取相轨迹方程时 一般有二种方法：一种是对式（7-35）直接进行积分。 显然，这只有在上述方程可以进行积分时才能运用。 另一种方法是先求出x和对t的函数关系，然后消去t， 5 从而求得相轨迹方程。下面举例加以说明。
x
0
x
22
④ = 0。系统特征根为一对纯虚根。系统的自 由运动为等幅正弦振荡。给定初始点，系统的相平 面图为围绕坐标原点的一簇椭圆（参阅例7-1），系 统相平面图:
山东大学 自动控制原理 7-2相平面法
[例7-5] 二阶线性系统当 = 0时的微分方程式为
2 n x 0 x
绘制相平面图。 解：
2 n x dx dx x
2 2 2 A x0 / n x0
对上式积分，便得相轨迹方程
x
x2
x
x2
2 n
A2
0
x 0
t
6
2. 图解法 目前比较常用的图解法有两种：等倾线法和 法。 下面介绍等倾线法。等倾线法的基本思想是采用直线 近似。如果我们能用简便的方法确定出相平面中任意 一点相轨迹的斜率，则该点附近的相轨迹便可用过这 点的相轨迹切线来近似。 设系统的微分方程式为
或
等倾线是过相平面原点的一些直线。当 = 0.5、n = 1 时的等倾线分布图 :
10
a= 1
x
1.2 B 1.4 2 3
2 n x x 2 n = 1/(a +1)
A
C
6
a= 1，k = a= 2，k = 1 a= 3，k = 1/2
x
2
1 0.8 0.4 0
13
7．3．3 线性系统的相平面图
线性系统是非线性系统的特例，对于许多非线性 一阶和二阶系统（系统中所含非线性环节可用分段折 线表示），常可以分成多个区间进行研究，而在各个 区间内，非线性系统运动特性可用线性微分方程描述； 此外，对于非线性微分方程，为研究各平衡状态附近 的运动特性，可在平衡点附近作增量线性化处理，即 对非线性微分方程两端的各非线性函数作泰勒展开， 并取一次项近似，获得平衡点处的增量线性微分方程。 因此，研究线性一阶、二阶系统的相轨迹及其特点是 十分必要的。下面研究线性一阶、二阶系统自由运动 的相轨迹，所得结论可作为非线性一阶、二阶系统相 平面分析的基础。
4.6+相平面法
相平面法是一种精确的方法，但它受到下列几点限制。
1）原则上，它仅适用于一阶、二阶系统。这是因为在平面上绘 制函数曲线是比较容易的。在三维空间中绘制三阶系统的相轨迹 可能，但很困难，而绘制三维以上空间中的轨迹则是不可能的。 因此，只有在相平面上分析一阶、二阶系统。对于线性部分是高 阶的系统，如果可以降为二阶，也可以用相平面法分析。
解析法是一种最基本的方法。当系统的微分方程 比较简单，或者系统中非线性特性可以分段线性化时， 可以用解析法绘制相平面图。
一般情况下，用解析法是比较困难、甚至不可能 的。因此，常用图解法。目前比较常用的图解法有等 倾线法和 法两种。
实验法是利用模拟计算机绘制相轨迹，即用模拟 计算机模拟所研究的系统，根据示波器的显示，或记 录仪，绘制出系统的相轨迹。
显 然 , 在 奇 点 (x10 , x20 ) 处 ,x1 0 ,x2 0 , 因 此 , 从 数 学 上 看，x1 x10 ，x2 x20 是微分方程(4.112)的定常解.反映在相平
面图上,因为奇点处相轨迹的斜率
dx2 dx1
x 2 x1
0是一不确定的
0
形式，所以可有多条相轨迹通过奇点,所以,奇点是相
0
x1
P x2
0
x1
Q x2
x2
0
x2
0
(4.117)
所考察系统在奇点附近的相轨迹的形状和一次项有密 切关系，因此，我们先讨论它的一次近似方程组的相 轨迹形状，然后借助于一次近似讨论原方程的奇点性 质。更一般地，考察一般二阶线性方程奇点的性质。
２ 二阶线性系统的相轨迹及奇点
考察二阶线性微分方程：
4.6.1 相平面
１ 相平面的定义
1）原则上，它仅适用于一阶、二阶系统。这是因为在平面上绘 制函数曲线是比较容易的。在三维空间中绘制三阶系统的相轨迹 可能，但很困难，而绘制三维以上空间中的轨迹则是不可能的。 因此，只有在相平面上分析一阶、二阶系统。对于线性部分是高 阶的系统，如果可以降为二阶，也可以用相平面法分析。
解析法是一种最基本的方法。当系统的微分方程 比较简单，或者系统中非线性特性可以分段线性化时， 可以用解析法绘制相平面图。
一般情况下，用解析法是比较困难、甚至不可能 的。因此，常用图解法。目前比较常用的图解法有等 倾线法和 法两种。
实验法是利用模拟计算机绘制相轨迹，即用模拟 计算机模拟所研究的系统，根据示波器的显示，或记 录仪，绘制出系统的相轨迹。
显 然 , 在 奇 点 (x10 , x20 ) 处 ,x1 0 ,x2 0 , 因 此 , 从 数 学 上 看，x1 x10 ，x2 x20 是微分方程(4.112)的定常解.反映在相平
面图上,因为奇点处相轨迹的斜率
dx2 dx1
x 2 x1
0是一不确定的
0
形式，所以可有多条相轨迹通过奇点,所以,奇点是相
0
x1
P x2
0
x1
Q x2
x2
0
x2
0
(4.117)
所考察系统在奇点附近的相轨迹的形状和一次项有密 切关系，因此，我们先讨论它的一次近似方程组的相 轨迹形状，然后借助于一次近似讨论原方程的奇点性 质。更一般地，考察一般二阶线性方程奇点的性质。
２ 二阶线性系统的相轨迹及奇点
考察二阶线性微分方程：
4.6.1 相平面
１ 相平面的定义
第7章--相平面法
若输出的一次谐波分量为
y1 (t) A1 cost B1 sint Y1 sin(t 1 )
输入的正弦量为 X sin t
则描述函数的数学表达式如式 （7-75） 所示：
返回子目录
N
Y1 X
e
e e0 e e0
e r c
得到 Te e Ku Tr r
假定
1 1 1
2 KT
2 kKT
54
（1）阶跃输入 r(t)=R
• 系统方程变为
Te e Ke 0
Te e kKe 0
图7-51 阶跃输入下得相轨迹
55
（2）输入信号r(t)=Vt+R
• 其中y(t)与c(t)两个状态变量之间满足导函数关 系
d
•
y(t) c(t) dt
•
• 将相变量定义为满足导函数关系的一组状态变 量。显然，相变量也不唯一
• 相平面法仅适用于研究二阶或一阶系统
2
c
o
a)
c(t)
c
o
t b)
o
c(t)
t
c)
3
• 图c是响应的时域曲线，图b是它的导函数曲 线，图a是以t为参变量,将输出响应特性及其导 函数特性绘在相平面上的曲线--输出响应特性 的“相轨迹”曲线 输出特性上既包含输出量大小的信息，也包含 它的导函数信息，特性上点的切线斜率就是该 点的导数
34
1、 在 c>h的区域
系统方程为
Tc(t) c(t) KM
c(t)
k1
k e(1/T )t 2
KMt
其中 k1 c0 (c0 KM )T k2 (c0 KM )T
相平面法
系统运动的速度和加速 0, ) 0， x f ( x , x ⑷ 在奇点处 x
度同时为0。 ⑸ 对于二阶系统来说，系统在奇点处不再发生运动， 处于平衡状态，故相平面的奇点亦称为平衡点。且
二阶系统的平衡点即为原点(0，0)。
3、线性二阶系统奇点的类型： ⑴ 焦点——特征根为共轭复根
根据这一方程可在相 平面上作一曲线，称为等倾线。
当轨迹经过该等倾线上任一点时，其切线的斜率都相
等，均为 。取
为若干不同 的常数，即可在相平
相平面上绘制出若干 条等倾线。在等倾线上各点处 作斜率为 的短直线，并以箭头表示切线方向，则 构成相轨迹的切线方向场。 所以，根据给定的初始条件，从初始点出发，便可
<一>奇点：
) 表示的二阶系统，其相轨 x f ( x , x 1、定义： 以微方
) dx f ( x, x 迹上每一点切线的斜率为 ， dx x
)和 x 同时为0， 若在某点处 f ( x ， x
0 dx 则称该点为相平面 即有 的不定形式， dx 0
的奇点。
的共轭复根（ 0 1) 稳 定 焦 点 ： 一 对 负 实 部 部的共轭复根（ - 1 0) 不 稳 定 焦 点 ： 一 对 正 实
2 n x dx dx x
dx n2 x d x 则 有x
2 x 2 x 2 A2 n
其中A是初条决定的积分常数，此为同心椭圆。
2、 0 1:
由第三章知： x ( t ) A e n t s in( d t ), d n 1
x02
01 x
x01
02 x
x01
x
度同时为0。 ⑸ 对于二阶系统来说，系统在奇点处不再发生运动， 处于平衡状态，故相平面的奇点亦称为平衡点。且
二阶系统的平衡点即为原点(0，0)。
3、线性二阶系统奇点的类型： ⑴ 焦点——特征根为共轭复根
根据这一方程可在相 平面上作一曲线，称为等倾线。
当轨迹经过该等倾线上任一点时，其切线的斜率都相
等，均为 。取
为若干不同 的常数，即可在相平
相平面上绘制出若干 条等倾线。在等倾线上各点处 作斜率为 的短直线，并以箭头表示切线方向，则 构成相轨迹的切线方向场。 所以，根据给定的初始条件，从初始点出发，便可
<一>奇点：
) 表示的二阶系统，其相轨 x f ( x , x 1、定义： 以微方
) dx f ( x, x 迹上每一点切线的斜率为 ， dx x
)和 x 同时为0， 若在某点处 f ( x ， x
0 dx 则称该点为相平面 即有 的不定形式， dx 0
的奇点。
的共轭复根（ 0 1) 稳 定 焦 点 ： 一 对 负 实 部 部的共轭复根（ - 1 0) 不 稳 定 焦 点 ： 一 对 正 实
2 n x dx dx x
dx n2 x d x 则 有x
2 x 2 x 2 A2 n
其中A是初条决定的积分常数，此为同心椭圆。
2、 0 1:
由第三章知： x ( t ) A e n t s in( d t ), d n 1
x02
01 x
x01
02 x
x01
x
相平面法——精选推荐
7.2 相平面法相平面法是一种在时域中求解二阶微分方程的图解法。
它不仅能分析系统的稳定性和自振荡，而且能给出系统运动轨迹的清晰图像。
相平面法一般适用于二阶非线性系统的分析。
7.2.1 相平面的基本概念图7-8 相轨迹291ξ=292293294295296297图7-11 确定相轨迹切线方向的方向场及相平面上的一条相轨迹7.2.3 非线性系统的相平面分析1. 利用二阶线性系统的相轨迹分析一类非线性系统例7-3 试确定下列方程的奇点及其类型，画出相平面图的大致图形。
（1）0sgn =++x x x （2）0||=+x x解 （1）系统方程可写为系统的奇点Ⅰ：1-=I e x Ⅱ：1=II e x系统特征方程为012=+s ，特征根j s ±=2,1，奇点为中心点。
画出系统的相平面图如图2987-12所示。
x 轴是两部分相轨迹的分界线，称之为“开关线”。
上、下两半平面的相轨迹分别是以各自奇点I e x 和II e x 为中心的圆，两部分相轨迹相互连接成为相轨迹图。
由图可见，系统的自由响应运动最终会收敛到)1,1(-之间。
奇点在)1,1(-之间连成一条线，称之为奇线。
图7-12 相轨迹图 图7-13 相轨迹图（2）系统方程可写为特征方程、特征根和奇点为Ⅰ：012=+s ，j s ±=2,1， 奇点0=eI x （中心点） Ⅱ：012=-s , 12,1±=s ， 奇点0=eII x (鞍点)画出系统的相平面图如图7-13所示。
x轴是开关线，左半平面相轨迹由鞍点决定，右半平面相轨迹由中心点确定。
由图可见，系统的自由响应总是会向x 轴负方向发散，系统不稳定。
2. 非线性系统相平面分析大多数非线性控制系统所含有的非线性特性是分段线性的，或者可以用分段线性特性来近似。
用相平面法分析这类系统时，一般采用“分区一衔接”的方法。
首先，根据非线性特性的线性分段情况，用几条分界线(开关线)把相平面分成几个线性区域，在各个线性区域内，各自用一个线性微分方程来描述。
相平面02
7.2 相平面法相平面法是一种在时域中求解二阶微分方程的图解法。
它不仅能分析系统的稳定性和自振荡，而且能给出系统运动轨迹的清晰图像。
相平面法一般适用于二阶非线性系统的分析。
7.2.1 相平面的基本概念1. 相平面和相轨迹设一个二阶系统可以用下面的常微分方程),(=+xxfx（7-1）来描述。
其中),(xxf 是x和x 的线性或非线性函数。
在一组非全零初始条件下()0(x 和)0(x不全为零)，系统的运动可以用解析解)(tx和)(tx 描述。
如果取x和x 构成坐标平面，则系统的每一个状态均对应于该平面上的一点，这个平面称相平面。
当t变化时，这一点在x-x 平面上描绘出的轨迹，表征系统状态的演变过程，该轨迹就叫做相轨迹（如图7-8(a)所示）。
相平面和相轨迹曲线簇构成相平面图。
相平面图清楚地表示了系统在各种初始条件下的运动过程。
例如，研究以方程22=++xxxωξω（7-2）描述的二阶线性系统在一组非全零初始条件下的运动。
当0=ξ时式（7-2）变为2=+xxω（7-3）初始条件为)0(xx=，)0(xx=，方程（7-3）对应有一对虚根，即ωjp±=-2,1式（7-3）的解为图7-8 相轨迹)sin(ϕω+=tAx（7-4）式中，2220ωxxA+=，arctanxxωϕ=设x为描述二阶线性系统的一个变量，取x为描述系统的另一状态变量，即)cos(ϕωω+==tAdtdxx （7-5）从式（7-4）、式（7-5）中消去变量t，可得出系统运动过程中两个状态变量的关系为222)(Axx=+ω这是一个椭圆方程。
椭圆的参数A取决于初始条件x和x 。
选取不同的一组初始条件，可得到不同的A，对应相平面上的相轨迹是不同的椭圆，这样便得到一个相轨迹簇。
0=ξ时的相平面图如图7-9所示，表明系统的响应是等幅周期运动。
图中箭头表示时间t增大的方向。
2.相轨迹的性质相平面的上半平面中，0>x ，相迹点沿相轨迹向x轴正方向移动，所以上半部分相轨迹箭头向右；同理，下半相平面0<x ，相轨迹箭头向左。
自动控制原理相平面法知识点总结
自动控制原理相平面法知识点总结自动控制原理相平面法是控制工程中的重要方法之一，通过将系统的转移函数映射到相平面上进行分析，可以得到系统的稳定性、动态响应等性能指标。
以下是对自动控制原理相平面法的知识点总结：1. 相平面的概念及表示相平面是用来表示系统传递函数的一种图形化工具，通常由实部和虚部组成。
相平面上的点代表传递函数在不同频率下的响应，可以通过绘制相平面上的轨迹来分析系统的动态特性。
2. 极点和零点极点和零点是传递函数中的重要概念。
极点是使传递函数分母等于零的根，影响系统的稳定性和动态响应；零点是使传递函数分子等于零的根，影响传递函数在不同频率下的响应特性。
3. 映射关系和稳定性判断相平面法中的映射关系将传递函数的极点映射到相平面上，通过分析相平面上的极点位置可以判断系统的稳定性。
一般来说，当系统的所有极点位于相平面的左半平面时，系统是稳定的；当存在极点位于右半平面时，系统是不稳定的。
4. 频率响应和幅频特性频率响应是指系统在不同频率下的输出响应情况。
相平面法可以通过绘制Bode图来分析系统的频率响应及其幅频特性。
幅频特性描述了系统的增益对频率的依赖关系，可以用来评估系统的稳定性和频率衰减特性。
5. 极点分布和动态响应传递函数的极点分布可以直接反映系统的动态响应特性。
相平面法可以通过绘制极点分布图来分析系统的阻尼比、超调量等动态性能指标。
例如，共轭复根表示系统存在振荡；实部大于零的极点会导致系统的不稳定和不良的动态特性。
6. 根轨迹分析根轨迹是描述系统极点随参数变化而形成的轨迹。
根轨迹可以通过绘制相平面上函数极点的运动轨迹来分析系统的稳定性和动态响应。
根轨迹的性质包括起点、终点、对称性等，可以提供关于系统稳定性和响应特性的重要信息。
7. 闭环稳定判据通过相平面法可以得到闭环传递函数的极点位置，进而判断闭环系统的稳定性。
常用的闭环稳定判据包括Nyquist判据和Routh-Hurwitz判据。
相平面法_HJ
dx dx dx x x f ( x, x ) d x dt dx
f ( x, x ) x
11
x 例 系统方程 x x 0 ，用等倾斜线法绘制系统相轨迹图。 dx x ) ( x x) x ( x x 解 dx x
为一常数。
根据上式可在相平面上绘制一条线，相轨迹通 过这条线上的各点时，其切线的斜率都相同， 称之为等倾线。如果取不同的值 1 , 2 ,则可 在相平面上绘制一系列的等倾线。
9
( x10 , x20 ) 1
x2
2
3
x1
4
图8-27 用等倾线法绘制相轨迹
相平面中所有等倾线上的短线，组成了相轨迹的切线场。
§8.4
相平面法
相平面法是Poincare在1885年首先提出来的， 它是一种求解一、二阶常微分方程的图解 法。这种方法的实质是将系统的运动过程 形象地转化为相平面上一个点的移动，通 过研究这个点移动的轨迹，就能获得系统 运动规律的全部信息。由于它能比较直观、 准确、全面地表征系统的运动状态，因而 获得广泛应用。
将（4）式代入（2）式整理得
( 4)
1
28
r r (1 r 2 ) 1
有r 0和1 r 2 0两种情况
(1) r 0
x1 0, x2 0 系统的平衡点（奇点）
b P ( x1 , x 2 ) 1 x 2 ( 0,0 )
系统特征方程为
I A (a d ) (ad bc ) 0
2
特征方程的根为
1, 2
a d (a d )2 4(ad bc ) 2
根据特征方程根的性质，可将奇点分为如下几种情况：
f ( x, x ) x
11
x 例 系统方程 x x 0 ，用等倾斜线法绘制系统相轨迹图。 dx x ) ( x x) x ( x x 解 dx x
为一常数。
根据上式可在相平面上绘制一条线，相轨迹通 过这条线上的各点时，其切线的斜率都相同， 称之为等倾线。如果取不同的值 1 , 2 ,则可 在相平面上绘制一系列的等倾线。
9
( x10 , x20 ) 1
x2
2
3
x1
4
图8-27 用等倾线法绘制相轨迹
相平面中所有等倾线上的短线，组成了相轨迹的切线场。
§8.4
相平面法
相平面法是Poincare在1885年首先提出来的， 它是一种求解一、二阶常微分方程的图解 法。这种方法的实质是将系统的运动过程 形象地转化为相平面上一个点的移动，通 过研究这个点移动的轨迹，就能获得系统 运动规律的全部信息。由于它能比较直观、 准确、全面地表征系统的运动状态，因而 获得广泛应用。
将（4）式代入（2）式整理得
( 4)
1
28
r r (1 r 2 ) 1
有r 0和1 r 2 0两种情况
(1) r 0
x1 0, x2 0 系统的平衡点（奇点）
b P ( x1 , x 2 ) 1 x 2 ( 0,0 )
系统特征方程为
I A (a d ) (ad bc ) 0
2
特征方程的根为
1, 2
a d (a d )2 4(ad bc ) 2
根据特征方程根的性质，可将奇点分为如下几种情况：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x2
0
x2
0
x1
x1
(a)稳定焦点
(b)不稳定焦点
17
图8-31 共轭复根对应的相轨迹
1, 2
a d (a d )2 4(ad bc ) 2
5）纯虚根
(a d ) 0, ad bc 0
奇点称为中心点。
x2
0
x1
图8-32
纯虚根对应的相轨迹
18
2、极限环
相平面图上的一根孤立的封闭相轨迹称为极限环。它对应系 统的自激振荡状态。极限环把相平面划分为内部平面和外部 平面两部分，相轨迹不能从环内穿越环进入环外，反之也不 能。
将（4）式代入（2）式整理得
( 4)
1
23
r r (1 r 2 ) 1
有r 0和1 r 2 0两种情况
(1) r 0
x1 0, x2 0 系统的平衡点（奇点）
b P ( x1 , x 2 ) 1 x 2 ( 0,0 )
为一常数。
根据上式可在相平面上绘制一条线，相轨迹通 过这条线上的各点时，其切线的斜率都相同， 称之为等倾线。如果取不同的值 1 , 2 ,则可 在相平面上绘制一系列的等倾线。
8
x2
1
( x10 , x20 )
2
x1
3
4
图8-27 用等倾线法绘制相轨迹
相平面中所有等倾线上的短线，组成了相轨迹的切线场。
P ( x1 , x2 ) P ( x1 , x2 ) P ( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )
Q( x1 , x2 ) Q( x1 , x2 ) Q( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )
另一反映系统运动特性的相轨迹是极限环（奇线）。 极限环是相平面上一根孤立的封闭的相轨迹，反映了系统 的自激振荡状态，它将无穷大的相平面分为两个部分，有 利于与奇点特性一起分析系统的运动特性。
10
二、奇点与极限环
1、奇点
奇点即为系统平衡点，它由方程组
x1 P ( x1 , x2 ) 0 x2 Q( x1 , x2 ) 0
若 P ( x1 , x2 ) 、Q( x1 , x2 ) 是解析的，在以x1为横坐 标轴，x2为纵坐标的平面上绘制一条x2与x1的关系 曲线，我们把这样一条轨线称为相轨迹，由一族 相轨迹组成的图像称为相平面图。
6
令
P ( x1 , x2 ) 0 Q( x1 , x2 ) 0
联立求解出的点 ( x10 , x20 ) 称为系统的平衡点。
由（2）式推得
(1) ( 2)
r cos r sin (1 r 2 ) r sin r cos
( 3)
2
将（3）式代入（1）式整理得 r r (1 r )
由（1）式推得
r sin r cos (1 r 2 ) r sin r cos
系统特征方程为
I A (a d ) (ad bc ) 0
2
特征方程的根为
1, 2
a d (a d )2 4(ad bc ) 2
根据特征方程根的性质，可将奇点分为如下几种情况：
13
1, 2
a d (a d )2 4(ad bc ) 2
P ( x1 , x 2 ) a x1 ( 0,0 )
令
P ( x1 , x 2 ) b x 2 ( 0,0 )
Q( x1 , x 2 ) d x 2 ( 0,0 )
12
Q( x1 , x 2 ) c x1 ( 0,0 )
则有
x1 ax1 bx2 x2 cx1 dx2
26
[例2] 如图所示非线性控制系统在t＝0时加上一个幅度为 6的阶跃输入，系统的初始状态为 e(0) 6, e(0) 0 ，问 经过多少秒，系统状态可到达原点。
e x 1 u
r
s+1
1 2s 2
y
图8-36 继电控制系统
解：列写运动方程
2 u y
1 u 1 x0 x0
对于一任意二阶非线性微分方程 或写成 令
f ( x , x ) 0 x
a1 ( x, x ) x a0 ( x, x ) x 0 x
x1 x x2 x1 x
x1 x2 x x2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1
代入初始条件 e(0) 6, e(0) 0 ， 有
A(6,0)
0 （2）
e
ee 0
c1 0, c2 6
e 0.5t 2 e 0.25t 6
x2 dx2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1 x1 dx1 x2
5
则有
将方程组写成一般形式有 x1 P ( x1 , x 2 )
x 2 Q( x1 , x 2 )
相轨迹上某点处 切线的斜率。
则
dx2 Q( x1 , x2 ) dx1 P ( x1 , x2 )
1) 同号相异实根
(a d )2 4(ad bc )
当 a d 0 时，两根同负，奇点称为稳定的节点； 当 a d 0时，两根同正，奇点称为不稳定的节点。
x2
x2
x1
(a) 稳定节点 （b）不稳定节点
x1
图8-28 特征方程根为同号相异实根的相轨迹
14
1, 2
a d (a d )2 4(ad bc ) 2
20
x2
x1
tx1Βιβλιοθήκη (a) 稳定的极限环x2
x1
t
x1
(b) 不稳定的极限环
x2
x1
t
x1
(c) 半稳定的极限环
21
[例1]
已知一非线性系统运动方程
2 2 x1 x2 x1 (1 x1 x2 ) 2 2 x2 x1 x2 (1 x1 x2 )
试分析系统的运动稳定性。
相轨迹的特点：
1、相平面上除平衡点外的任意一点只有一根相轨迹通过。
dx2 Q 0 2、由式 可知，相轨迹在平衡点附近切线斜 dx1 P 0 率不定，意味着有无穷多根相轨迹到达或离开平衡点。
7
相轨迹的画法——等倾线法
dx2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1 Q( x1 , x2 ) 令 dx1 x2 P ( x1 , x2 )
R 0
x1
2 2 x1 x2 1为稳定的极限环，平衡 (0， 为不稳定的焦点。 点 0)
25
三、用相平面法分析非线性系统
用相平面法分析非线性系统的步骤：
1、根据非线性特性将相平面划分为若干区域，建立每个 区域的线性微分方程来描述系统的运动特性； 2、根据分析问题的需要，适当选择相平面坐标轴； 3、根据非线性特性建立相平面上切换线方程； 4、求解每个区域的微分方程，绘制相轨迹; 5、平滑地将各个区域的相轨迹连起来，得到整个系统的相 轨迹。据此可用来分析非线性系统的运动特性。
联立求解得到 ( x10 , x20 ) 。 将 P ( x1 , x2 ) 、Q( x1 , x2 ) 在平衡点 ( x10 , x20 ) 附近展开 成台劳级数，以便研究该点附近相轨迹的形状及运动 特性。奇点只有可能出现在x轴上。
11
忽略高阶无穷小， 一般情况下令 x10 x20 0
则有
解：
将直角坐标系转化为极坐标系 令 x1 r cos , x2 r sin
则
x1 r cos r sin x r sin r cos
2
22
代入原方程得
r cos r sin r sin r cos (1 r 2 ) r sin r cos r cos r sin (1 r 2 )
奇点(0,0)为不稳定焦点，附近相轨迹为发散振荡。 24
( 2) r 1
2 2 x1 x2 1，单位圆 （系统的极限环）
在单位圆内任取一点A，由于OA<r=1， 由方程有 r r(1 r 2 ) 0 则封闭相轨迹内的相轨迹向单位圆逼近。
A
x2
B
在单位圆外任取一点B，由于OB>r=1， 由方程有 r r(1 r 2 ) 0 则封闭相轨迹外的相轨迹向单位圆逼近。
从相轨迹起始点 ( x10 , x20 ) 出发，平滑的将相邻等倾线上 的短线连起来，即得系统相轨迹。 9
1 , 2 , 3 ,表示相轨迹通过这些等倾线时切线的斜率。
绘制相轨迹的目的是为了分析系统的运动特性； 由于系统的平衡点有无穷根相轨迹离开或到达，因此平衡 点附近的相轨迹，最能反映系统的运动特性。 平衡点又称为奇点。
§8.4
相平面法
相平面法是Poincare在1885年首先提出来的， 它是一种求解一、二阶常微分方程的图解 法。这种方法的实质是将系统的运动过程 形象地转化为相平面上一个点的移动，通 过研究这个点移动的轨迹，就能获得系统 运动规律的全部信息。由于它能比较直观、 准确、全面地表征系统的运动状态，因而 获得广泛应用。
2) 异号实根
ad bc 0
奇点称为鞍点。
x2
0
x1
图8-29 鞍点对应的相轨迹
15
1, 2
a d (a d )2 4(ad bc ) 2
0
x2
0
x1
x1
(a)稳定焦点
(b)不稳定焦点
17
图8-31 共轭复根对应的相轨迹
1, 2
a d (a d )2 4(ad bc ) 2
5）纯虚根
(a d ) 0, ad bc 0
奇点称为中心点。
x2
0
x1
图8-32
纯虚根对应的相轨迹
18
2、极限环
相平面图上的一根孤立的封闭相轨迹称为极限环。它对应系 统的自激振荡状态。极限环把相平面划分为内部平面和外部 平面两部分，相轨迹不能从环内穿越环进入环外，反之也不 能。
将（4）式代入（2）式整理得
( 4)
1
23
r r (1 r 2 ) 1
有r 0和1 r 2 0两种情况
(1) r 0
x1 0, x2 0 系统的平衡点（奇点）
b P ( x1 , x 2 ) 1 x 2 ( 0,0 )
为一常数。
根据上式可在相平面上绘制一条线，相轨迹通 过这条线上的各点时，其切线的斜率都相同， 称之为等倾线。如果取不同的值 1 , 2 ,则可 在相平面上绘制一系列的等倾线。
8
x2
1
( x10 , x20 )
2
x1
3
4
图8-27 用等倾线法绘制相轨迹
相平面中所有等倾线上的短线，组成了相轨迹的切线场。
P ( x1 , x2 ) P ( x1 , x2 ) P ( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )
Q( x1 , x2 ) Q( x1 , x2 ) Q( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )
另一反映系统运动特性的相轨迹是极限环（奇线）。 极限环是相平面上一根孤立的封闭的相轨迹，反映了系统 的自激振荡状态，它将无穷大的相平面分为两个部分，有 利于与奇点特性一起分析系统的运动特性。
10
二、奇点与极限环
1、奇点
奇点即为系统平衡点，它由方程组
x1 P ( x1 , x2 ) 0 x2 Q( x1 , x2 ) 0
若 P ( x1 , x2 ) 、Q( x1 , x2 ) 是解析的，在以x1为横坐 标轴，x2为纵坐标的平面上绘制一条x2与x1的关系 曲线，我们把这样一条轨线称为相轨迹，由一族 相轨迹组成的图像称为相平面图。
6
令
P ( x1 , x2 ) 0 Q( x1 , x2 ) 0
联立求解出的点 ( x10 , x20 ) 称为系统的平衡点。
由（2）式推得
(1) ( 2)
r cos r sin (1 r 2 ) r sin r cos
( 3)
2
将（3）式代入（1）式整理得 r r (1 r )
由（1）式推得
r sin r cos (1 r 2 ) r sin r cos
系统特征方程为
I A (a d ) (ad bc ) 0
2
特征方程的根为
1, 2
a d (a d )2 4(ad bc ) 2
根据特征方程根的性质，可将奇点分为如下几种情况：
13
1, 2
a d (a d )2 4(ad bc ) 2
P ( x1 , x 2 ) a x1 ( 0,0 )
令
P ( x1 , x 2 ) b x 2 ( 0,0 )
Q( x1 , x 2 ) d x 2 ( 0,0 )
12
Q( x1 , x 2 ) c x1 ( 0,0 )
则有
x1 ax1 bx2 x2 cx1 dx2
26
[例2] 如图所示非线性控制系统在t＝0时加上一个幅度为 6的阶跃输入，系统的初始状态为 e(0) 6, e(0) 0 ，问 经过多少秒，系统状态可到达原点。
e x 1 u
r
s+1
1 2s 2
y
图8-36 继电控制系统
解：列写运动方程
2 u y
1 u 1 x0 x0
对于一任意二阶非线性微分方程 或写成 令
f ( x , x ) 0 x
a1 ( x, x ) x a0 ( x, x ) x 0 x
x1 x x2 x1 x
x1 x2 x x2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1
代入初始条件 e(0) 6, e(0) 0 ， 有
A(6,0)
0 （2）
e
ee 0
c1 0, c2 6
e 0.5t 2 e 0.25t 6
x2 dx2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1 x1 dx1 x2
5
则有
将方程组写成一般形式有 x1 P ( x1 , x 2 )
x 2 Q( x1 , x 2 )
相轨迹上某点处 切线的斜率。
则
dx2 Q( x1 , x2 ) dx1 P ( x1 , x2 )
1) 同号相异实根
(a d )2 4(ad bc )
当 a d 0 时，两根同负，奇点称为稳定的节点； 当 a d 0时，两根同正，奇点称为不稳定的节点。
x2
x2
x1
(a) 稳定节点 （b）不稳定节点
x1
图8-28 特征方程根为同号相异实根的相轨迹
14
1, 2
a d (a d )2 4(ad bc ) 2
20
x2
x1
tx1Βιβλιοθήκη (a) 稳定的极限环x2
x1
t
x1
(b) 不稳定的极限环
x2
x1
t
x1
(c) 半稳定的极限环
21
[例1]
已知一非线性系统运动方程
2 2 x1 x2 x1 (1 x1 x2 ) 2 2 x2 x1 x2 (1 x1 x2 )
试分析系统的运动稳定性。
相轨迹的特点：
1、相平面上除平衡点外的任意一点只有一根相轨迹通过。
dx2 Q 0 2、由式 可知，相轨迹在平衡点附近切线斜 dx1 P 0 率不定，意味着有无穷多根相轨迹到达或离开平衡点。
7
相轨迹的画法——等倾线法
dx2 a1 ( x1 , x2 ) x2 a0 ( x1 , x2 ) x1 Q( x1 , x2 ) 令 dx1 x2 P ( x1 , x2 )
R 0
x1
2 2 x1 x2 1为稳定的极限环，平衡 (0， 为不稳定的焦点。 点 0)
25
三、用相平面法分析非线性系统
用相平面法分析非线性系统的步骤：
1、根据非线性特性将相平面划分为若干区域，建立每个 区域的线性微分方程来描述系统的运动特性； 2、根据分析问题的需要，适当选择相平面坐标轴； 3、根据非线性特性建立相平面上切换线方程； 4、求解每个区域的微分方程，绘制相轨迹; 5、平滑地将各个区域的相轨迹连起来，得到整个系统的相 轨迹。据此可用来分析非线性系统的运动特性。
联立求解得到 ( x10 , x20 ) 。 将 P ( x1 , x2 ) 、Q( x1 , x2 ) 在平衡点 ( x10 , x20 ) 附近展开 成台劳级数，以便研究该点附近相轨迹的形状及运动 特性。奇点只有可能出现在x轴上。
11
忽略高阶无穷小， 一般情况下令 x10 x20 0
则有
解：
将直角坐标系转化为极坐标系 令 x1 r cos , x2 r sin
则
x1 r cos r sin x r sin r cos
2
22
代入原方程得
r cos r sin r sin r cos (1 r 2 ) r sin r cos r cos r sin (1 r 2 )
奇点(0,0)为不稳定焦点，附近相轨迹为发散振荡。 24
( 2) r 1
2 2 x1 x2 1，单位圆 （系统的极限环）
在单位圆内任取一点A，由于OA<r=1， 由方程有 r r(1 r 2 ) 0 则封闭相轨迹内的相轨迹向单位圆逼近。
A
x2
B
在单位圆外任取一点B，由于OB>r=1， 由方程有 r r(1 r 2 ) 0 则封闭相轨迹外的相轨迹向单位圆逼近。
从相轨迹起始点 ( x10 , x20 ) 出发，平滑的将相邻等倾线上 的短线连起来，即得系统相轨迹。 9
1 , 2 , 3 ,表示相轨迹通过这些等倾线时切线的斜率。
绘制相轨迹的目的是为了分析系统的运动特性； 由于系统的平衡点有无穷根相轨迹离开或到达，因此平衡 点附近的相轨迹，最能反映系统的运动特性。 平衡点又称为奇点。
§8.4
相平面法
相平面法是Poincare在1885年首先提出来的， 它是一种求解一、二阶常微分方程的图解 法。这种方法的实质是将系统的运动过程 形象地转化为相平面上一个点的移动，通 过研究这个点移动的轨迹，就能获得系统 运动规律的全部信息。由于它能比较直观、 准确、全面地表征系统的运动状态，因而 获得广泛应用。
2) 异号实根
ad bc 0
奇点称为鞍点。
x2
0
x1
图8-29 鞍点对应的相轨迹
15
1, 2
a d (a d )2 4(ad bc ) 2