江苏大数学分析--格林公式.曲线积分与路径无关性共44页

格林公式与路径无关的条件
格林公式是求解曲线上某一点极线的公式,它描述了一个函数$f(x,y)$ 在两个坐标系 $x$ 和 $y$ 之间的变换关系。

与路径无关的条件指的是在求解格林公式时,需要满足以下条件:
1. 曲线在两个坐标系之间的变换是线性的。

即对于任意两条曲线,它们变换后的位置是线性相关的。

2. 坐标系是平移不变的。

即当曲线在两个坐标系之间移动时,坐标系的平移量是不变的。

3. 极线是经过曲线上某一点的邻域内最短径路的直线。

即当曲线上一点被移动时,它的极线经过该点所连接的邻域内任意一点,且这条直线是曲线上某一点的最短径路。

如果曲线在两个坐标系之间的变换满足以上三个条件,那么可以用格林公式求解曲线上某一点的极线。

需要注意的是,如果曲线在两个坐标系之间的变换不满足以上三个条件,则格林公式将无法正确地求解极线。

第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念：当区域D 的边界L 由一条或几条光滑曲线所组成时，规定边界曲线的正方向为：当人沿边界行走时，区域D 总在他的左边. 与正方向相反的方向称为负方向，记为-L.定理21.11：若函数P(x,y), Q(x,y)在闭区域D 上连续，且有连续的一阶偏导数，则有格林公式：⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线，并取正方向.证：根据区域D 的不同形状，可分三种情形来证明： (1)若区域D 既是x 型区域，又是y 型区域(如图1)，即 平行于坐标轴的直线和L 至多交于两点，该区域D 可表示为： φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证：-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2)，则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域，然后逐块按(1)得到它们的格林公式，相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3，则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3)， 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注：格林公式可写为：⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1：计算⎰AB xdy ，其中曲线AB 为半径为r 的圆在第一象限部分. 解：如图，对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2：计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解：⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界，∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注：在格林公式中，令P=-y, Q=x ，则得到一个计算平面区域D 的面积S D 的公式：S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3：如图，计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解：曲线⌒AMO由函数y=x ax -, x ∈[0,a]， 直线OA 为直线y=0， ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念：若对于平面区域D 上任一封闭曲线，皆可不经过D 以外的点而连续收缩于属于D 的某一点，则称此平面区域为单连通区域，否则称为复连通区域。

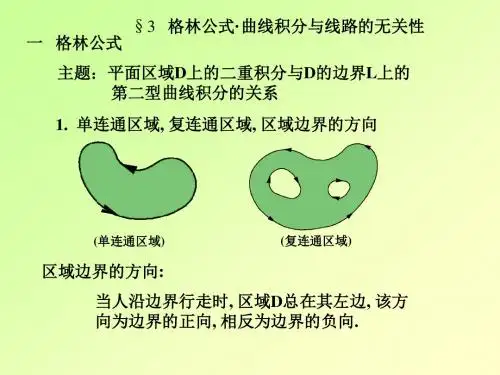
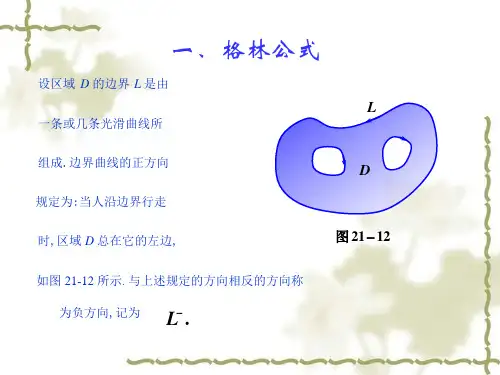
§ 3 Green 公式 曲线积分与路径无关性一、 格林Green 公式Green 公式揭示了平面上某区域内的二重积分与该边界上的一个特定的第二类曲线积分之间的关系. Green 公式是N--L 公式在 R 2中的推广.1 闭区域的正面与边界正向的规定平面上的单连通区域、多连通区域 P227—228在区域D 2R ⊂内，如果任意两条有同一起点和同一终点的曲线，其中一条总可以在D 内连续的变动为另一条，则称区域D 是单连通的；否则就是多连通闭区域的正面与边界正向的规定搭配: 右手螺旋定向, 即以右手拇指表示区域的正面( 理解为拇指“站立在” 区域的正面上 ), 则其余四指( 弯曲 )表示边界的正向. 右手螺旋定向法则还可表述为: 人站立在区域的正面的边界上, 让区域在人的左方. 则人前进的方向为边界的正向. 参阅P224图21--10. 若以L 记正向边界, 则用-L 或L -表示反向（或称为负向）边界.2 格林Green 公式及其证明定理21.11 设闭区域D 边界D ∂由光滑曲线或逐段光滑曲线组成. 若函数P 和Q 在闭区域D ⊂R 2上连续,且有连续的一阶偏导数, 则有⎰⎰⎰+=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D L Qdy Pdx dxdy y P x Q , （1）其中L 为区域D 的正向边界.证明 P224—226注 将格林Green 公式的证明过程分为几个习题，由同学们解答.然后老师小结.Green 公式又可记为⎰⎰⎰+=∂∂∂∂DL Qdy Pdx dxdy QP y x . 3 格林Green 公式的一个应用由逐段光滑封闭曲线所围区域D 的面积公式|D |⎰-=L ydx xdy 21, L 为D 的正向边界. （2）补例1 计算由星形线 ) 20 ( sin , cos 33π≤≤==t t b y t a x 所界的面积. 补例2 用Green 公式求曲线 a x y y x 333=+ 所围图形的面积.4 应用格林Green 公式简化某些二类曲线积分的计算举例有时用Green 公式，将二类曲线积分转化为二重积分来计算. 对环路积分, 可直接应用Green 公式. 对非闭路积分, 常采用附加上一条线使变成环路积分的技巧.例1 计算积分⎰ABxdy , 其中A , ) , 0 (r B ) 0 , (r . 曲线AB 为圆周222r y x =+在第一象限中的部分. （P226）解法1 ( 直接计算积分 ) 曲线AB 的方程为 20 , sin , cos π≤≤==t t r y t r x .方向为自然方向的反向. 因此⎰⎰-=⎪⎭⎫ ⎝⎛+-=-=AB r t t r tdt r xdy 222022242sin 2121cos πππ. 解法2 ( 用Green 公式 ) 补上线段BO 和OA ( O 为坐标原点 ), 成闭路. 设所围区域为D , 注意到∂D 为反向, 以及0=⎰BOA, 有⎰ABxdy ⎰⎰⎰⎰∂-=-=-=DBOADr dxdy xdy xdy 24π.例2 计算积分 I =⎰+-L y x ydxxdy 22, 其中L 为任一不包含原点的闭区域D 的边界. （P226）解 2222),( , ),(yx xy x Q y x y y x P +=+-=. (P 和Q 在D 上有连续的偏导数). ()2222222yx x y y x y x y P +-=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂, 22222)(y x x y x Q +-=∂∂. 于是, I =⎰⎰⎰=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=D Ldxdy y P x Q 0.注 将此例推广为（参见P203） 计算积分 I =⎰+-L y x ydxxdy 22, 其中L 为任一不通过原点的正向闭曲线.补例3 计算积分⎰++Ldy x y x dx xy )(22, 其中L 是由曲线 222 , x y x y ==,4 , 3==xy xy 所围区域D 的边界, 取正向.解 ,),(2xy y x P = x y x y x Q +=2),(. 1 , 12 , 2=∂∂-∂∂⇒+=∂∂=∂∂yP x Q xy x Q xy y P . ⎰⎰⎰=DLdxdy .作代换xy v x yu ==, 2, 在此代换之下 , 区域D 变为UV 平面上的区域 } 43 , 21|),( {≤≤≤≤='v u v u D .=-=∂∂xy x x yy x v u 2312),(),(u x y 332-=-, u v u y x 31),(),( =∂∂⇒. 于是,⎰⎰⎰⎰⎰⎰⎰'====DD Lu dv du dudv u dxdy 2143331 ⎰==21212ln 31ln 3131u u du . 补例4 计算积分⎰⎰-Dy dxdy e 2, D : 10 , 1≤≤≤≤x y x . 解 令2),( , 0),(y xe y x Q y x P -==, 有⎰⎰⎰∂+=DDdy y x Q dx y x P ),(),( .域D 为三角形, 三个顶点为O , ) 0 , 0 (A ) 1 , 1 (, B ) 1 , 0 (.⇒⎰⎰⎰⎰⎰⎰=-==+=∂∂BOO ADDDdy y x Q dy y x Q dx y x P ),(),(),()1(21211101022----=-==⎰e e dx xe x x . 注 此例将二重积分化为二类曲线积分转来计算.二、曲线积分与路线无关性第二类曲线积分不仅与曲线的起点和终点有关，而且也与所沿的积分路径有关. 对同一个起点和同一个终点，沿不同的路径所得到的第二类曲线积分一般是不相同的. 在什么样的条件下第二类曲线积分与积分路径无关而仅与曲线的起点和终点有关呢？下面我们先在平面中情形来讨论这个问题。