什么是曲线积分？？ 1. 设L为xOy平面上的一条光滑的简单曲线弧,f(x,y)在L上有界，在L上任意插入一点列M1,M2,M3…,Mn 把L 分成 n个小弧段ΔLi的长度为ds，又Mi(x,y)是L上的任一点，作乘积f(x,y)i*ds,并求和即Σ f(x,y)i*ds，记λ=max(ds) ，若Σ f(x,y)i*ds的极限在当λ→0的时候存在，且极限值与L的分法及Mi在L的取法无关，则称极限值为f(x,y)在L上对弧长的曲线积分，记为：∫f(x,y)*ds ；其中f(x,y)叫做被积函数，L叫做积分曲线，对弧长的曲线积分也叫第一类曲线积分。 2. 曲线积分的类别: 曲线积分分为：对弧长的曲线积分 （第一类曲线积分） 对坐标轴的曲线积分（第二类曲线积分） 两种曲线积分的区别主要在于积分元素的差别；对弧长的曲线积分的积分元素是弧长元素ds；例如：对L的曲线积分∫f(x,y)*ds 。对坐标轴的曲线积分的积分元素是坐标元素dx或dy，例如：对L’的曲线积分∫P（x,y）dx+Q(x,y)dy。但是对弧长的曲线积分由于有物理意义，通常说来都是正的，而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号33。
3. 两种曲线积分的联系： 对弧长的曲线积分和对坐标轴的曲线积分是可以互相转化的，利用弧微分公式ds=√[1+(dy/dx)^2]*dx; 或者ds=√[1+(dx/dy)^2]*dy;这样对弧长的曲线积分都可以转换成对坐标轴的曲线积分了。
在数学中，曲线积分或路径积分是积分的一种。积分函数的取值沿的不是区间，而是特定的曲线，称为积分路径。曲线积分有很多种类，当积分路径为闭合曲线时，称为环路积分或围道积分。 在曲线积分中，被积的函数可以是标量函数或向量函数。积分的值是路径各点上的函数值乘上相应的权重（一般是弧长，在积分函数是向量函数时，一般是函数值与曲线微元向量的标量积）后的黎曼和。带有权重是曲线积分与一般区间上的积分的主要不同点。物理学中的许多简单的公式（比如说
）在推广之后都是以曲线积分的形式出现（ ）。曲线积分在物理学中是很重要的工具，例如计算电场或重力场中的做功，或量子力学中计算粒子出 4. 格林公式 【定理】设闭区域由分段光滑的曲线围成,函数及在上具有一阶连续偏导数,则有 (1) ∮cP(x,y)dx+Q(x,y)dy=∫∫D(dQ/dx-dP/dy)dxdy 其中是的取正向的边界曲线. 公式(1)叫做格林(green)公式. 【证明】先证 假定区域的形状如下(用平行于轴的直线穿过区域,与区域边界曲线的交点至多两点) 易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域给予证明即可. 另一方面,据对坐标的曲线积分性质与计算法有 因此 再假定穿过区域内部且平行于轴的直线与的的边界曲线
的交点至多是两点,用类似的方法可证 综合有 当区域的边界曲线与穿过内部且平行于坐标轴( 轴或轴 )的任何直线的交点至多是两点时,我们有
5., 若曲线积分在开区域内与路径无关,那它仅与曲线的起点与终点的坐标有关.假设曲线的起点为,终点为,可用记号 或 来表示,而不需要明确地写出积分路径. 显然,这一积分形式与定积分非常相似, 事实上,我们有下列重要定理 【定理一】设是一个单连通的开区域,函数,在内具有一阶连续偏导数,且 【证明】依条件知,对内任意一条以点为起点,点为终点的曲线,曲线积分 与路径无关,仅与的起点和终点的坐标有关,亦即, 确为点的单值函数. 下面证明 由于可以认为是从点沿内任何路径到点的曲线积分,取如下路径,有 类似地可证明 因此 【定理二】设是单连通的开区域,,在上具有一阶连续偏导数,则在内为某一函数全微分的充要条件是 在内恒成立. 【证明】显然,充分性就是定理一 下面证明必要性 若存在使得 ,则 由于 ,在 内连续, 则二阶混合偏导数适合等式 从而 【定理三】设是一个单连通的开区域, 函数,在内具有一阶连续偏导数, 若存在二元函数使得 则 其中,是内的任意两点. 【证明】由定理1知,函数 适合 于是 或 因此 (是某一常数 ) 即 而 这是因为由点沿任意内的路径回到点构成一条封闭曲线,故 因此 □ 【确定的全微分函数的方法】 因为,而右端的曲线积分与路径无关,为了计算简便,可取平行于坐标轴的直线段所连成的折线作为积分路径(当然折线应完全属于单连通区域).
------------------------------------------------------- 【证明】先证 假定区域的形状如下(用平行于轴的直线穿过区域,与区域边界曲线的交点至多两点) 易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域给予证明即可. 另一方面,据对坐标的曲线积分性质与计算法有 因此 再假定穿过区域内部且平行于轴的直线与的的边界曲线的交点至多是两点,用类似的方法可证 综合有 当区域的边界曲线与穿过内部且平行于坐标轴( 轴或轴 )的任何直线的交点至多是两点时,我们有 , 同时成立. 将两式合并之后即得格林公式 注:若区域不满足以上条件,即穿过区域内部且平行于坐标轴的直线与边界曲线的交点超过两点时,可在区域内引进一条或几条辅助曲线把它分划成几个部分区域,使得每个部分区域适合上述条件,仍可证明格林公式成立. 6. 牛顿—莱布尼兹公式baaFbFdxxF)()()('表示：)('xF在区间ba,上的定积分可以通过它的原函数)(xF在这个区间端点的值来表
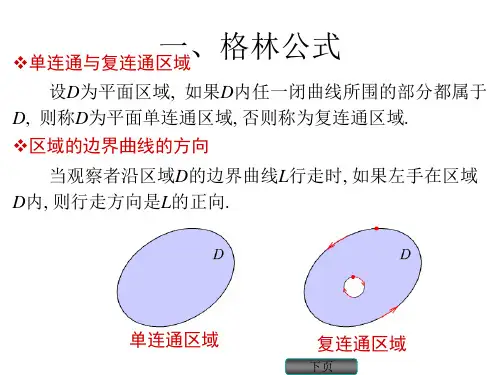
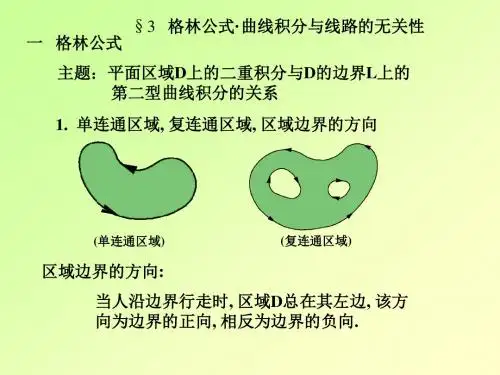
达．而格林公式表示：在平面区域D上的二重积分可以通过沿闭区域D的边界曲线L的曲线积分来表达．这样，牛顿——莱布尼兹公式成为格林公式的特殊情形． 平面单连通域的概念．设D为平面区域，如果D内任一闭曲线所围的部分都属于D，则称D为平面单连通区域，否则称为复连通区域． 例如：平面上的圆形区域1|,22yxyx，上半平面0|,yyx
都是单连通区域，圆环形区域10|,,41|,2222yxyxyxyx都是复连通区
域． 对平面区域D的边界曲线L，规定L的正向如下：当观察者沿L的方向行走时，D总在他的左边．例如D
是边界曲线L及l所围成的复连通域(图8)，作为D的正向边界，L的正向是逆时针方向，而l的正向是顺时针方向． 定理1 设闭区域D由分段光滑的曲线L围成，函数),(yxP及),(yxQ在D上具有一阶连续偏导数，则有
LDQdyPdxdxdyyPxQ)(
, (1)
其中L是D的取正向的边界曲线．公式(1)叫做格林公式． 证 先假设区域D既是X型又是Y型的情形，即穿过区域D且平行坐标轴的直线与D的边界曲线L的交点恰好为两点(图9)
设bxaxyxyxD),()(|,21，因为yP
连续，所以 babaxxDdxxxPxxPdxdyyyxPdxdyyP))(,())(,(
),(
12)(
)(2
1
.
另一方面，对坐标的曲线积分
LLLbaabbadxxxPxxPdxxxPdxxxPPdxPdxPdx12))(,())(,())(,())(,(
2121
.
因此得 LDPdxdxdyyP. (2) 类似地，设dycyxyyxD),()(|,21，则可证 LDQdydxdy
x
Q
. (3)
由于D既是X型又是Y型的区域，(2)(3)同时成立，二式合并即得公式(1) 区域D既是X型又是Y型这样的要求是相当严格的，但是对于一般情形，即区域D不满足这个条件时，我们可在D内引进辅助线把D分成有限个部分闭区域，使得每个部分闭区域都满足这个条件，如图10，应用公式(1)于每个部分区域，即可得证．因此，一般地对于由分段光滑曲线围成的闭区域公式(1)都成立．证毕．
注 (1) 格林公式中左端二重积分的被积函数是yPxQ，而且在D内偏导连续．这是初学者容易记错或者忽略的地方．右端曲线积分中曲线L对区域D来说都是正向，这也是需要注意的． (2) 对于复连通区域D，格林公式右端应包括沿区域D的全部边界的曲线积分．例如对图8的复连通域1D(阴影部分)格林公式应为
LlDQdyPdxQdyPdxdxdy
yPx
Q
1.
其中L、l是D的取正向的闭曲线． (3) 格林公式揭示出二重积分与平面曲线积分之间的联系，同时也给出了通过二重积分计算曲线积分的一个重要公式．许多情况，曲线积分化为二重积分计算往往是方便的．当然有些二重积分也可以化为曲线积分来计算，但是在化为曲线积分时，被积表达式并不是唯一
的．例如，Dxdxdy化为曲线积分时，即可以是dyxL221，也可以是dxxy或者是xydxdyxL22121，等等．
格林公式的一个简单应用，在公式(1)中取yP，xQ，即得LDydxxdydxdy2
，上式左端为闭区域D的面积A的两倍，因此区域
D的面积A可以用下面的曲线积分计算
