格林公式及其在曲线积分求解中的应用
- 格式:doc
- 大小:226.34 KB
- 文档页数:7








微积分是数学的一个分支,其中有一个重要概念就是曲线积分。
曲线积分是对曲线上的函数进行积分的过程,它在实际应用中具有广泛的意义和重要性。
而格林公式则是曲线积分的一个基本定理,它连接了曲线积分和面积积分之间的关系。
首先,我们来了解一下曲线积分的概念。
在平面坐标系中,考虑一条光滑曲线C,我们要对C上的一个函数f(x, y)进行积分。
曲线积分分为两种类型:第一类曲线积分和第二类曲线积分。
第一类曲线积分是对函数在曲线上的取值进行积分,记作∮Cf(x, y)ds。
第二类曲线积分则是将函数与曲线的切向量进行内积后再进行积分,记作∮Cf(x, y)·dr。
曲线积分的计算方法与路径有关,也与函数在路径上的取值有关。
接下来,我们介绍一下格林公式。
格林公式是曲线积分的一个基本定理,它说明了曲线积分与面积积分之间的关系。
设有一个光滑闭合曲线C,这个曲线将一个有限的区域D围起来。
设有两个偏导数连续的函数P(x, y)和Q(x, y),则有∮C[P(x, y)dx + Q(x, y)dy] = ∬D(Qx - Py)dA其中,Qx和Py分别表示P和Q对x和y的偏导数,dA表示微小面积元。
利用格林公式,我们可以将曲线积分转化为面积积分的形式进行计算,这样更加方便和简化。
同时,格林公式还可以推广到更高维的情况下,用于计算空间中曲面积分和体积积分。
最后,我们来看一个实际应用中的例子。
假设有一个平面曲线C,它是一个三角形的边界,我们要计算曲线积分∮C(x^2 + y^2)ds。
首先,我们可以找到这个三角形的顶点,并确定它的边界方程。
然后,利用格林公式,将曲线积分转化为面积积分。
计算面积积分后,我们就可以得到曲线积分的结果。
总之,微积分中的曲线积分与格林公式是一个重要的内容。
曲线积分是对曲线上函数的取值进行积分的过程,而格林公式则把曲线积分与面积积分建立起了联系。
通过格林公式,我们可以将曲线积分转化为面积积分进行计算,这样更加方便和简化。


格林公式及其在曲线积分求解中的应用.南昌工程学院《数分选讲》课程设计题目格林公式及其在曲线积分求解中的应用课程名称数分选讲系院理学院专业信息与计算科学班级XXXX年6月11日至XXXX年6月15日什么是曲线积分??1. 设L为xOy平面上的一条光滑的简单曲线弧,f(x,y)在L上有界,在L上任意插入一点列M1,M2,M3…,Mn 把L 分成n 个小弧段ΔLi的长度为ds,又Mi(x,y)是L上的任一点,作乘积f(x,y)i*ds,并求和即Σ f(x,y)i*ds,记λ=max(ds) ,若Σ f(x,y)i*ds的极限在当λ→0的时候存在,且极限值与L的分法及Mi在L的取法无关,则称极限值为f(x,y)在L上对弧长的曲线积分,记为:∫f(x,y)*ds ;其中f(x,y)叫做被积函数,L叫做积分曲线,对弧长的曲线积分也叫第一类曲线积分。
2. 曲线积分的类别:曲线积分分为:对弧长的曲线积分(第一类曲线积分)对坐标轴的曲线积分(第二类曲线积分)两种曲线积分的区别主要在于积分元素的差别;对弧长的曲线积分的积分元素是弧长元素ds;例如:对L的曲线积分∫f(x,y)*ds 。
对坐标轴的曲线积分的积分元素是坐标元素dx或dy,例如:对L’的曲线积分∫P(x,y)dx+Q(x,y)dy。
但是对弧长的曲线积分由于有物理意义,通常说来都是正的,而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号33。
3. 两种曲线积分的联系:对弧长的曲线积分和对坐标轴的曲线积分是可以互相转化的,利用弧微分公式ds=√[1+(dy/dx) ]*dx; 或者ds=√[1+(dx/dy) ]*dy;这样对弧长的曲线积分都可以转换成对坐标轴的曲线积分了。
在数学中,曲线积分或路径积分是积分的一种。
积分函数的取值沿的不是区间,而是特定的曲线,称为积分路径。
曲线积分有很多种类,当积分路径为闭合曲线时,称为环路积分或围道积分。
在曲线积分中,被积的函数可以是标量函数或向量函数。
微积分是数学的一门重要的分支,它研究的是函数的变化与极限。
在微积分中,曲线积分是一个重要的概念,它与格林公式有着密切的关系,并广泛应用于实际问题的求解中。
首先,我们来了解一下曲线积分的概念。
曲线积分是指在曲线上对向量场进行积分的过程。
对于一个曲线C,可以将其参数化为r(t)=<x(t), y(t)>,其中t是一个参数,x(t)和y(t)是关于t的函数。
向量场F=<P(x, y), Q(x, y)>可以表示为F=<P(r(t)), Q(r(t))>。
那么曲线积分可以表示为∫F·dr,其中dr是曲线上的微元向量。
曲线积分在物理、工程等领域有着广泛的应用。
例如,在机械工程中,可以用曲线积分来计算力的沿曲线的积分,以及在闭合路径上力的环量。
另外,在电磁学中,可以利用曲线积分来计算电场强度、磁感应强度等物理量。
接下来,我们来介绍一下格林公式。
格林公式是曲线积分与二重积分之间的重要联系。
它实质上是一个积分定理,可以将曲线上的积分转化为曲线所围成区域上的二重积分。
格林公式的数学表达为∮Pdx+Qdy=∬[∂Q/∂x-∂P/∂y]dxdy,其中P和Q是关于x和y的函数,[∂Q/∂x-∂P/∂y]是P和Q的二阶偏导数交叉相减的结果。
这个公式表明,在一个有界的、光滑的区域D上,曲线积分∮Pdx+Qdy等于区域D上∂Q/∂x-∂P/∂y的二重积分。
格林公式的应用范围很广泛。
它可以用于计算曲线围成的区域的面积、重心、质心等物理量。
例如,在工程中,常常需要计算复杂形状的物体的重心位置,可以通过将物体分解为小区域,然后运用格林公式来计算每个小区域的质心位置,最后将各个小区域的质心位置加权平均得到整个物体的重心位置。
此外,格林公式还可以用于计算闭合路径上的曲线积分,例如计算电场强度的环量。
在电磁学中,电场强度可以表示为E=<-∂Φ/∂x, -∂Φ/∂y>,其中Φ是电势函数,而电场强度的环量可以用曲线积分来表示。
第三节格林公式及应用第三节格林公式及应用第三节格林公式及应用3.1自学目标掌握格林公式并会运用平面曲线积分与路径无关的条件,会求二元函数全微分的原函数.3.2内容提要1.格林公式设闭区域d由分段扁平的曲线l围起,函数p?x,y?,q?x,y?在d内具备一阶已连续略偏导数,则存有q?p?pdx?qdy?dxdy,lx?y?d?其中l是d的取正向的边界曲线.【备注】(1)格林公式阐明了二重积分与曲线分数的联系.(2)d可以就是为丛藓科扭口藓相连区域.(3)l为正向的封闭曲线,p?x,y?,q?x,y?在d内具有一阶连续偏导数,两者缺一不可.在利用格林公式计算曲线积分时,若l不封闭,则考虑适当补边使之封闭;若在d内函数有奇点,应考虑将奇点挖掉.(4)当p??y,q?x时,纡出来半封闭曲线所围区域的面积a?1xdy?ydx??l22.平面上曲线积分与路径无关的条件设立区域g就是一个单相连域,函数p?x,y?,q?x,y?在区域g内具备一阶已连续的偏导数,则曲线分数必须条件就是pdxqdy在g内与路径无关(或沿g内任意闭曲线的曲线积分为零)的充l?q?p??x?y在g内恒设立.【注】若曲线积分与路径无关,在进行曲线积分的计算时,可以在g内选择简单路径,选择折线是常用的方法.3.二元函数的全微分算草设区域g是一个单连通域,函数p?x,y?,q?x,y?在区域g内具有一阶连续的偏导数,则p(x,y)dx?q(x,y)dy在g内为某一函数u(x,y)的全微分的充要条件是qpxy在g内恒设立.(x,y)xyu(x,y)??或(x0,y0)p(x,y)dx?q(x,y)dy??p(x,y0)dx??q(x,y)dyx0y0yxu(x,y)??q(x0,y)dy??p(x,y)dx.y0x0其中m0(x0,y0)就是区域g内适度选取的一点.【注】设区域g是一个单连通域,函数p?x,y?,q?x,y?在区域g内具有一阶连续的偏导数,则以下四个命题等价:命题1曲线分数pdxqdy在g内与路径无关;l命题2在g内任一一条闭合曲线l,存有pdxqdy=0;l命题3表达式p?x,y?dx?q?x,y?dy在g内就是某个二元函数的全微分,即为存有u?x,y?使得du?p?x,y?dx?q?x,y?dy;命题4qp在g内每一点处成立.?x?yl4.计算pdxqdy的通常步骤qp,?x?y(1)首先验证是否(2)若qp,考察l是否封闭,若封闭用格林公式;?x?y??xt?,t求,若不封闭取参数?y??t,(3)若来求.qp,也实地考察l与否半封闭,若半封闭结果为0;若不半封闭,用折线或用补线?x?y3.3典型例题与方法基本题型i:利用格林公式谋第二类曲线分数基准1填空题x22(1)设f(x,y)在d:?y?1内具有连续的二阶偏导数,c为顺时针方向的椭圆4x2?y2?1,则??c[?3y?fx'(x,y)]dx?fy'(x,y)dy?________.42?2f??xyi?xyj促进作用下沿圆周x2?y2?a2的顺时针方向运动一周,(2)设立质点在力则力f所作的功w?________.求解(1)由格林公式,注意到曲线c为顺时针方向,得[?3y?f'(x,y)]dx?f'(x,y)dy[f\x,y)?f''(x,y)?3]d?3d?6?cxyyxxydd故应填?6?.222(2)设曲线c:x?y?a围成的区域为d,则2?a1422223wxydx?xydy??(x?y)dxdy??d??d?a?c?002d14故应填??a.2例2选择题22(1)设立曲线c为椭圆4x?y?1,并挑正向,则曲线分数??c?ydx?xdy等同于().4x2?y2(a)0;(b)2?;(c)??;(d)?.(2)已知xaydxydy就是某函数的全微分,则a等同于().2?x?y?(a)?1;(b)0;(c)?2;(d)2.22解(1)因为4x?y?1,代入得ydxxdy2dxdy.??c4x2?y2c?ydx?xdyd故挑选(d).(2)p(x,y)?x?ay?x?y?,q(x,y)?2y?x?y?2,于是p(a2)xayq2y,,33yxxyxypq由可得a?2,故选(d).?y?xx2y2例3计算??x?y?dx??x?y?dy,其中l为椭圆线2?2?1的正向.lab【分析】l为半封闭扁平曲线挑正向,合乎格林公式的条件,需用格林公式展开排序.求解x?y?dxx?y?dy=1?1?dxdy2dxdy2?ab,lddx2y2其中d为椭圆域2?2?1.ab例4计算x?y?dxx?y?dyx?y22l,其中l为圆x2?y2?a2的正向.【分析】此题可直接用公式x?acost,y?asint,0?t?2?计算.也可用积分曲线方程化简被积函数,再用格林公式计算.下面给出后一种解法.求解l?x?y?dxx?y?dy?x2?y21a2l?x?y?dxx?y?dya21?1?d?d??2?a2??2?.2a222【方法点击】该题不能直接利用格林公式计算,因为被积函数在d:x?y?a内不满足具有一阶连续偏导数的条件,但由曲线l的方程化简被积函数后,就满足了格林公式的条件,可再用格林公式计算.基准5排序3x2x?是半圆弧.(ye?my)dx?(3ye?m)dy,c为从e到f再到g,fg?cyf(2,1)oe(1,0)g(3,0)x图3-1【分析】似乎c为从e至g的分段扁平曲线,可以轻易化成的定分数展开排序,但排序较繁杂.如果补边ge,则可以沦为半封闭曲线,利用格林公式排序后再乘以ge上的分数,可以得所求分数值.但必须特别注意曲线的方向.pq3y2exm,3y2ex,解p?ye?my,q?3ye?m,?y?x3x2x?q?p??m.添加直线ge,利用格林公式得,?x?y?c(y3ex?my)dy?(3y2ex?m)dy+?pdx?qdy??gemdxdy??m(1?).??4d??所以,c(y3exmy)dy(3y2exm)dy=(1)m-gepdxqdy=m(1).44【方法点击】补边是利用格林公式解决非封闭曲线积分的重要方法,但须满足格林公式的条件.例6计算段.2l?ydx?xdy,其中沿曲线自点?2,0?至?0,0?的存有向弧y?2x?x?ly图3-2ox【分析】本题可利用l的方程直接求解,得到解法一.还可以通过补边,使其满足格林公式的条件,再利用格林公式计算.数学分析一如图3-2右图,l的方程y?2x?x2,dy?0?1?x2??ydx?xdy??2x?x?x??l?2?2x?x2?1?x2x?x2dx,故dx.数学分析二补线l1:?由格林公式0x2(方向与x轴的方向一致),l1与曲线l围成闭区域d,y?0ydx?xdy??ll?l1?ydx?xdyydx?xdyl1而q?p?ydx?xdyl?l1xydxdy?2dxdy.dd从而l1ydxxdy0.ydx?xdy.l。
浅谈格林公式在计算曲线积分中的应用作者:李玉荣来源:《学业》2019年第05期摘要:本文通过举例展示了格林公式及由格林公式推导出的四个等价命题在计算第二型曲线积分中发挥着非常重要的作用。
关键词:格林公式;曲线积分格林公式将平面闭区域D上的二重积分与沿闭区域D的边界曲线L上的第二型曲线积分联系了起来。
一、下面先给出格林公式及由格林公式推导出的四个等价命题定理(格林公式):设闭区域D由分段光滑的曲线L围成,若函数P(x,y)及Q(x,y)在D上具有一階连续偏导数,则有其中L是D的取正向的边界曲线。
由格林公式可以推出以下四个等价命题,即在前提条件成立的情况下,以下四个命题是等价的。
这四个命题在曲线积分的计算中发挥着非常重要的作用。
条件:j区域D是单连通区域(若对于平面区域D上任一封闭曲线,皆可不经过D以外的点而连续收缩于属于D的某一点,则称此平面区域D为单连通区域,通俗地说,单连通区域是没有“洞”的区域);k;P(x,y)及Q(x,y)在D内具有连续的一阶偏导数。
四个等价命题:1、在D内,与路径无关,只与起点、终点有关。
2、3、在D内存在,使4、在D注意:以上四个命题等价的两个条件缺一不可。
二、举例1、当给定曲线较复杂时,可以利用积分与路径无关,选取简单路线。
例1 计算,其中L为由点到点的曲线弧。
解:由于曲线较复杂,所以先检验积分是否与路径无关。
满足第4个命题,从而由命题1,原积分与路径无关。
所以选取L为的折线,2、当给定曲线较复杂,但积分与路径有关时,可以补充曲线使其封闭,然后利用格林公式来计算。
例2 计算,其中L为由点(a,0)到点(0,0)的上半圆周x2+y2=ax,y10。
解即,积分与路径有关。
补充曲线为(0,0)到(a,0)的线段,所以原式3、若是某个函数的全微分,则可利用曲线积分求出该函数,即解:由于所以是某一函数的全微分,且参考文献:[1]高等数学[M].北京:高等教育出版社.2014[2]数学分析[M].北京:高等教育出版社.2010。
南昌工程学院
《数分选讲》课程设计题目格林公式及其在曲线积分求解中的应用
课程名称数分选讲
系院理学院
专业信息与计算科学
班级 2012级1班
学生姓名魏志辉
学号 2012101316
指导教师禹海雄
设计起止时间:2015年6月11日至2015年6月15日
什么是曲线积分??
1.设L为xOy平面上的一条光滑的简单曲线弧,f(x,y)在L上有界,在L上任意
插入一点列M1,M2,M3…,Mn 把L 分成 n个小弧段ΔLi的长度为ds,又Mi(x,y)是L上的任一点,作乘积f(x,y)i*ds,并求和即Σ f(x,y)i*ds,记λ=max(ds) ,若Σ f(x,y)i*ds的极限在当λ→0的时候存在,且极限值与L的分法及Mi在L的取法无关,则称极限值为f(x,y)在L上对弧长的曲线积分,记为:∫f(x,y)*ds ;其中f(x,y)叫做被积函数,L叫做积分曲线,对弧长的曲线积分也叫第一类曲线积分。
2.曲线积分的类别:
曲线积分分为:对弧长的曲线积分(第一类曲线积分)
对坐标轴的曲线积分(第二类曲线积分)
两种曲线积分的区别主要在于积分元素的差别;对弧长的曲线积分的积分元素是弧长元素ds;例如:对L的曲线积分∫f(x,y)*ds 。
对坐标轴的曲线积分的积分元素是坐标元素dx或dy,例如:对L’的曲线积分∫P (x,y)dx+Q(x,y)dy。
但是对弧长的曲线积分由于有物理意义,通常说来都是正的,而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号33。
3.两种曲线积分的联系:
曲线积分与一般区间上的积分的主要不同点。
物理学中的许多简单的公式(比如说
)在推广之后都是以曲线积分的形式出现()。
曲线积分在物理学中是很重要的工具,例如计算电场或重力场中的做功,或量子力学中计算粒子出4.格林公式
【定理】设闭区域由分段光滑的曲线围成,函数及在上具有一阶连续偏导数,则有
(1) ∮cP(x,y)dx+Q(x,y)dy=∫∫D(dQ/dx-dP/dy)dxdy
其中是的取正向的边界曲线.
公式(1)叫做格林(green)公式.
【证明】先证
假定区域的形状如下(用平行于轴的直线穿过区域,与区域边界曲线的交点至多两点)
易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域给予证明即可.
另一方面,据对坐标的曲线积分性质与计算法有
因此
再假定穿过区域内部且平行于轴的直线与的的边界曲线的交点至多是两点,用类似的方法可证
综合有
当区域的边界曲线与穿过内部且平行于坐标轴( 轴或轴 )的任何直线的交点至多是两点时,我们有
5., 若曲线积分在开区域内与路径无关,那它仅与曲线的起点与终点的坐
标有关.假设曲线的起点为,终点为,可用记号
或
来表示,而不需要明确地写出积分路径.
显然,这一积分形式与定积分非常相似, 事实上,我们有下列重要定理【定理一】设是一个单连通的开区域,函数,在内具有一阶连续偏导数,且【证明】依条件知,对内任意一条以点为起点,点为终点的曲线,曲线积分与路径无关,仅与的起点和终点的坐标有关,亦即, 确为点的单值函数.
下面证明
由于可以认为是从点沿内任何路径到点的曲线积分,取如下路径,有
类似地可证明
因此
【定理二】设是单连通的开区域,,在上具有一阶连续偏导数,则在内为某一函数全微分的充要条件是
在内恒成立.
【证明】显然,充分性就是定理一
下面证明必要性
若存在使得 ,则
由于 ,在内连续, 则二阶混合偏导数适合等式
从而
【定理三】设是一个单连通的开区域, 函数,在内具有一阶连续偏导数, 若存在二元函数使得
则
其中,是内的任意两点.
【证明】由定理1知,函数
适合
于是或
因此 (是某一常数 )
即
而
这是因为由点沿任意内的路径回到点构成一条封闭曲线,故 因此 □
【确定的全微分函数的方法】
因为,而右端的曲线积分与路径无关,为了计算简便,可取平行于坐标轴的直线段所连成的折线作为积分路径(当然折线应完全属于单连通区域).
-------------------------------------------------------
【证明】先证
假定区域的形状如下(用平行于轴的直线穿过区域,与区域边界曲线的交点至多两点)
易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域给予证明即可.
另一方面,据对坐标的曲线积分性质与计算法有
因此
再假定穿过区域内部且平行于轴的直线与的的边界曲线的交点至多是两点,用类似的方法可证
综合有
当区域的边界曲线与穿过内部且平行于坐标轴( 轴或轴 )的任何直线的交点至多是两点时,我们有
,
同时成立.
将两式合并之后即得格林公式
注:若区域不满足以上条件,即穿过区域内部且平行于坐标轴的直线与边界曲线的交点超过两点时,可在区域内引进一条或几条辅助曲线把它分划成几个部分区域,使得每个部分区域适合上述条件,仍可证明格林公式成立.
6. 牛顿—莱布尼兹公式⎰-=b a a F b F dx x F )()()('表示:)('x F 在区间[]b a ,上的定积分可以通过它的原函数)(x F 在这个区间端点的值来表达.而格林公式表示:在平面区域D 上的二重积分可以通过沿闭区域D 的边界曲线L 的曲线积分来
表达.这样,牛顿——莱布尼兹公式成为格林公式的特殊情形.
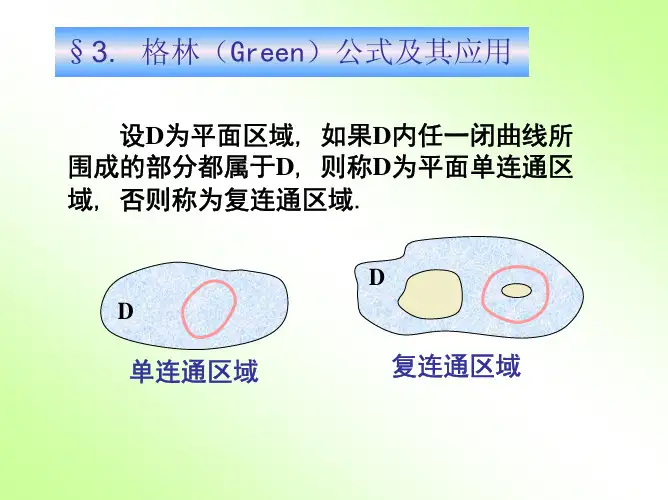
平面单连通域的概念.设D 为平面区域,如果D 内任一闭曲线所围的部分都属于D ,则称D 为平面单连通区域,否则称为复连通区域.
例如:平面上的圆形区域(){
}1|,22<+y x y x ,上半平面(){}0|,>y y x 都是单连通
区域,圆环形区域(){}(){}
10|,,41|,2222<+<<+<y x y x y x y x 都是复连通区域. 对平面区域D 的边界曲线L ,规定L 的正向如下:当观察
者沿L 的方向行走时,D 总在他的左边.例如D 是边界曲线L
及l 所围成的复连通域(图8),作为D 的正向边界,L 的正向
是逆时针方向,而l 的正向是顺时针方向.
定理1 设闭区域D 由分段光滑的曲线L 围成,函数),(y x P 及),(y x Q 在D 上具有一阶连续偏导数,则有
⎰⎰⎰+=∂∂-∂∂L D Qdy Pdx dxdy y P x Q )(
, (1)
其中L 是D 的取正向的边界曲线.公式(1)叫做格林公式.
证 先假设区域D 既是X 型又是Y 型的情形,即穿过区域D 且平行坐标轴的直线与D 的边界曲线L 的交点恰好为两点(图9)
设(){}b x a x y x y x D ≤≤≤≤=),()(|,21ϕϕ,因为y P
∂∂连
续,所以
{}⎰⎰⎰⎰⎰-=⎭⎬⎫⎩⎨⎧∂∂=∂∂b a b a x x D
dx x x P x x P dx dy y y x P dxdy y P ))(,())(,(),(12)()(21ϕϕϕϕ.
另一方面,对坐标的曲线积分
{}⎰⎰⎰⎰⎰⎰-=+=+=L L L b a a b b
a dx x x P x x P dx x x P dx x x P Pdx Pdx Pdx 12))(,())(,())(,())(,(2121ϕϕϕϕ.
因此得 ⎰⎰⎰=∂∂-L D Pdx dxdy y P . (2)
类似地,设(){}d y c y x y y x D ≤≤≤≤=),()(|,21ϕϕ,则可证
⎰⎰⎰=∂∂L D Qdy dxdy x Q . (3)
由于D 既是X 型又是Y 型的区域,(2)(3)同时成立,二式合并即得公式(1)
区域D 既是X 型又是Y 型这样的要求是相当严格的,但
是对于一般情形,即区域D 不满足这个条件时,我们可在D
内引进辅助线把D 分成有限个部分闭区域,使得每个部分闭
区域都满足这个条件,如图10,应用公式(1)于每个部分区
域,即可得证.因此,一般地对于由分段光滑曲线围成的闭
区域公式(1)都成立.证毕.
注 (1) 格林公式中左端二重积分的被积函数是
y P x Q ∂∂-∂∂,而且在D 内偏导连续.这是初学者容易记错或者忽略的地方.右端曲线积分中曲线L 对区域D 来说都是正向,这也是需要注意的.
(2) 对于复连通区域D ,格林公式右端应包括沿区域D 的全部边界的曲线积分.例如对图8的复连通域1D (阴影部分)格林公式应为
⎰⎰⎰⎰+++++=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂L l D Qdy Pdx Qdy Pdx dxdy y P x Q 1.
其中+L 、+l 是D 的取正向的闭曲线.
(3) 格林公式揭示出二重积分与平面曲线积分之间的联系,同时也给出了通过二重积分计算曲线积分的一个重要公式.许多情况,曲线积分化为二重积分计算往往是方便的.当然有些二重积分也可以化为曲线积分来计算,但是在化为曲线积分时,被积表达式并不是唯一的.例如,⎰⎰D xdxdy 化为曲线积分时,即可以是dy x L ⎰221,也可以是()dx xy ⎰-或者是xydx dy x L -⎰22121,等等.
格林公式的一个简单应用,在公式(1)中取y P -=,x Q =,即得⎰⎰⎰-=L D ydx
xdy dxdy 2,上式左端为闭区域D 的面积A 的两倍,因此区域D 的面积A 可以用下面的曲线积分计算。