格林公式曲线积分与路径无关的条件ppt
- 格式:ppt
- 大小:432.50 KB
- 文档页数:19



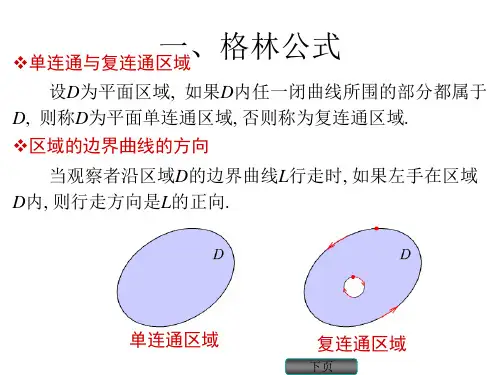
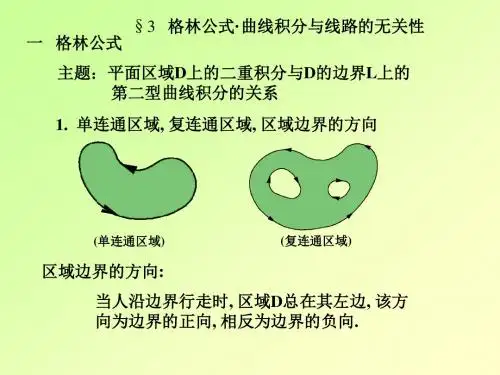






*点击以上标题可直接前往对应内容格林公式设区域D组成.规定为:时, 区域D如图21-12 所示为负方向,记为定理20.1若函数(,),(,)P x y Q x y 在闭区域D 上有连续的一阶偏导数, 则有∂∂-=+∂∂⎛⎫⎪⎝⎭⎰⎰⎰d d d ,LD Q P P x Q y x y σ (1)这里L 为区域D 的边界曲线, 并取正方向.公式(1)称为格林公式.证根据区域D 的不同形状, 这里对以下三种情形(i)若D 既是x 型又是y 型区域(图21-13),作出证明:12()(),,x y x a x b ϕϕ≤≤≤≤又可表为12()(),.y x y y ψψαβ≤≤≤≤1()y x ϕ=2()y x ϕ=这里和分 CAE 分别是曲线和 CBE 的方程.ACBAEB 别为曲线和的方程,O x1()x ϕβαAb EaBC2()x ϕyD图21-13则D 可表为1()x y ψ=2()x y ψ=和则而d DQx σ∂∂⎰⎰21((),)d ((),)d Q y y y Q y y yββααψψ=-⎰⎰ (,)d (,)d CBECAEQ x y y Q x y y=-⎰⎰ (,)d (,)d CBEEACQ x y y Q x y y=+⎰⎰(,)d .LQ x y y =⎰于是,21()()d d y y Q y x x βψαψ∂=∂⎰⎰d (,)d .L DP P x y x y σ∂-=∂⎰⎰⎰ 将上述两个结果相加即得d d d .L D Q P P x Q y x y σ⎛⎫∂∂-=+ ⎪∂∂⎝⎭⎰⎰⎰ (ii)若区域D 是由一条按段光滑的闭曲线围成,且可用几段光滑曲线将D 分成有限个既是x 型同理又可证得又是y 型的子区域, 格林公式, 然后相加即可.则可逐块按(i) 得到它们的如图21-14 所示的区域是y 型的区域1D d Q P σ⎛⎫∂∂- ⎪⎰⎰123d D D D Q P x y ⎛⎫∂∂=- ⎪∂∂⎝⎭⎰⎰于是可将它分成三个既是123d d d d d d L L L P x Q y P x Q y P x Q y =+++++⎰⎰⎰d d .LP x Q y =+⎰后, D 的边界则由 23,,,,,,AB L BA AFC CE L ECCE 及构成. 由(ii)知CGAd D Q P x y σ⎛⎫∂∂- ⎪∂∂⎝⎭⎰⎰ {}23(d d )ABL BAAFCCEL ECCGAP x Q y =++++++++⎰⎰⎰⎰⎰⎰⎰⎰()231(d d )L L L P x Q y =+++⎰⎰⎰ d d .LP x Q y =+⎰注1 并非任何单连通区域都可分解为有限多个既是x y 型又是型区域的并集, 31sin ,(0,1];1;0;1y x x y x x x=∈=-==所围成的区域便是如此.例如由注2为便于记忆, 格林公式(1) 也可写成下述形式:d d d .LDx y PQP x Q y σ∂∂∂∂=+⎰⎰⎰注3 应用格林公式可以简化某些曲线积分的计算.请看以下二例:第一象限部分(图21-16).解对半径为r 的四分之一圆域D, 应用格林公式:d d LDx y σ--=⎰⎰⎰d d d .OAABBOx y x y x y =++⎰⎰⎰由于d 0,d 0,OA BO x y x y ==⎰⎰ d d AB Dx y σ=-⎰⎰⎰例1 计算d ,ABx y ⎰其中曲线是半径为r 的圆在AB Ox2116-图BL-AD y因此21π.4r =-例2 计算22d d ,L x y y xI x y -=+⎰ 其中L 为任一不包含原点的闭区域D 的边界线.解因为2222222,()x y x x x y x y ⎛⎫∂-= ⎪∂++⎝⎭2222222,()y y xy x y x y ⎛⎫∂--= ⎪∂++⎝⎭于是,由格林公式2222=d 0,D x y x x y y x y σ⎡⎤⎛⎫⎛⎫∂∂--=⎢⎥ ⎪ ⎪∂+∂+⎝⎭⎝⎭⎣⎦⎰⎰22d d L x y y x x y -+⎰在格林公式中, 令,,P y Q x =-=则得到一个计算平面区域D 的面积S D 的公式:1d d d .2D L DS x y y x σ==-⎰⎰⎰ (2)例3 计算抛物线2()(0)x y ax a +=>与x 轴所围图形的面积(图21-17).解曲线 AMO 由函数,[0,]y ax x x a =-∈表示, O NA 0,y =为直线于是1d d 2D S x y y x =-⎰ x2117-图O(,0)A a NMy 11d d d d 22ONA AMOx y y x x y y x =-+-⎰⎰1d d 2AMOx y y x =-⎰011)d 22a a x ax x x ax ⎡⎤⎛⎫=---⎢⎥ ⎪⎝⎭⎣⎦⎰020111d d .2246a a a ax x x x a ⎛⎫=-== ⎪⎝⎭⎰⎰在第二十章§2 中计算第二型曲线积分的开始两个例子中, B 为终点的曲线积分, 若所沿的路线不同, 则其积分值也不同, 点有关, 与路线的选取无关. 什么条件下, 它的值与所沿路线的选取无关.首先介绍单连通区域的概念. 若对于平面区域D 内任一封闭曲线, 皆可不经过D曲线积分与路线的无关性读者可能已经注意到, 在例1中, 以A 为起点但在例2 中的曲线积分值只与起点和终本段将讨论曲线积分在一封闭曲线所围成的区域只含有D 中的点.定理21.12更通俗地说, 单连通区域就是没有“洞”的区域, 复连通区域则是有“洞”的区域.设D 是单连通闭区域. 若函数(,),P x y (,)Q x y 在D 内连续, 且具有一阶连续偏导数, 下四个条件等价:(i)沿D 内任一按段光滑封闭曲线L ,有d d 0;LP x Q y +=⎰(ii)对D 中任一按段光滑曲线L ,曲线积分d d LP x Q y +⎰则以与路线无关, 只与L 的起点及终点有关;定理21.12d d P x Q y +(,)u x y (iii) 是D 内某一函数的全微分, 即在D 内有d d d ;u P x Q y =+(iv)在D 内处处成立.P Q y x∂∂=∂∂d d d d ARBBSAP x Q y P x Q y=+++⎰⎰ d d 0,ARBSAP x Q y =+=⎰所以d d d d .ARBASBP x Q y P x Q y +=+⎰⎰ d d d d ARBASBP x Q y P x Q y+-+⎰⎰2119-图BRS(i) 沿D 内任一按段光滑封闭曲线L , 有d d 0;LP x Q y +=⎰(ii)对D 中任一按段光滑曲线L ,曲线积分d d L P x Q y +⎰与路线无关, 只与L 的起点及终点有关;⇒ ARB ASB 证(i)(ii) 如图21-19, 设与为联结点A ,B 的任意两条按段光滑曲线, 由(i) 可推得D 内任意一点. dABP x ⎰故当(,)B x y 在积分值是(,B x y (,)d d .ABu x y P x Q y =+⎰取x ∆充分小, 使(,),C x x y D +∆∈则函数(,)u x y 对于x 的偏增量(图21-20)⇒(A (ii)(iii) 设(,x u u x x ∆=+∆ d ACP x Q =+⎰因为在D d ACP x Q ∴+⎰因直线段BC d d ABP x Q =+⎰(ii)对D 中任一按段光滑曲线L ,曲线积分d d L P x Q y +⎰与路线无关, 只与L 的起点及终点有关;d d P x Q y +(,)u x y (iii) 是D 内某一函数的全微分, 即在D 内有d d d ;u P x Q y =+00lim lim (,)(,).x x x u uP x x y P x y x x θ∆→∆→∆∂==+∆=∂∆同理可证(,).uQ x y y∂=∂所以证得d d d .u P x Q y =+d d x BC u P x Q y∆=+⎰(,)d (,),x xxP t y t P x x y x θ+∆==+∆∆⎰0 1.θ≤≤其中(,)P x y 根据在D 上连续, 于是有(ii)对D 中任一按段光滑曲线L ,曲线积分d d L P x Q y +⎰与路线无关, 只与L 的起点及终点有关;d d P x Q y +(,)u x y (iii) 是D 内某一函数的全微分, 即在D 内有d d d ;u P x Q y =+⇒(,),u x y (iii)(iv) 设存在函数使得d d d ,u P x Q y =+因此(,)(,),(,)(,).x y P x y u x y Q x y u x y ==于是由(,),(,),x y yx P Q u x y u x y y x∂∂==∂∂以及P , Q 具有一阶连续偏导数, 便可知道在D 内每一点处都有(,)(,),x y yx u x y u x y =d d P x Q y +(,)u x y (iii) 是D 内某一函数的全微分, 即在D 内有d d d ;u P x Q y =+(iv)在D 内处处成立.P Qy x∂∂=∂∂.P Qy x∂∂=∂∂即(iv)⇒(i) 设L 为D 内任一按段光滑封闭曲线, σ所围的区域为. 含在D 内. 的条件, 就得到由于D 为单连通区域, 所以区域σd d d 0.L Q P P x Q y xy σσ⎛⎫∂∂+=-= ⎪∂∂⎝⎭⎰⎰⎰ 上面我们将四个条件循环推导了一遍, 这就证明了它们是相互等价的.记L P Q y x∂∂=∂∂应用格林公式及在D 内恒有(i) 沿D 内任一按段光滑封闭曲线L , 有d d 0;LP x Q y +=⎰(iv)在D 内处处成立.P Qy x∂∂=∂∂应用定理21.12 中的条件(iv)考察第二十章§2 中的在例1中(,),(,).P x y xy Q x y y x ==-由于,1,,P Q P Qx y x y x∂∂∂∂==-≠∂∂∂∂故积分与路线有关.在例2 中(,),(,),P x y y Q x y x ==由于例1 与例2. 1,P Qy x∂∂==∂∂所以积分与路线无关.例4 计算22(0.5)d (0.5)d ,(0.5)L x y x x y yx y--+-+-+⎰其中到点D (0,1) 的路径(见图21-21). 分析如果第二型曲线积分路径无关的条件,L 为沿着右半圆周221(0)x y x +=≥由点A (0, -1)图21-21xyO(0,1)A -(1,1)B -(1,1)C (0,1)D1L 2L LE在某单连通区域内满足与积分路径, 使易于计算.则可改变记220.5(,),(0.5)x yP x y x y--=-+22222(0.5)2(0.5).[(0.5)]Q P x y y x x y x y ∂∂--++-==∂∂-+220.5(,).(0.5)x yQ x y x y-+=-+易知除去点E (0.5, 0) 外,处处满足1L (0,1)A -(1,1),B -(1,1),C 设为由点到点再到点最图21-21xyO(0,1)A -(1,1)B -(1,1)C (0,1)D1L 2L LE解(0,1)D 的折线段. 后到点1L L 因为与可被包含在某一不含奇点E 的单连通区域内, 所以有22(0.5)d (0.5)d (0.5)Lx y x x y yx y--+-+-+⎰1(,)d (,)d L P x y x Q x y y=+⎰()(,)d (,)d ABBCCDP x y x Q x y y=+++⎰⎰⎰1102220110.50.5 1.5d d d (0.5)10.25(0.5)1x y x x y x x y x -++-=++-++-+⎰⎰⎰4arctan0.52arctan2.=+注1 定理21.12中对“单连通区域”的要求是重要的.何不包含原点的单连通区域, 已证得在这个区域内的任何封闭曲线L 上, 皆有22d d 0.L x y y xx y -=+⎰(3)如本例若取沿y 轴由点A 到点D 的路径, 虽2L 然算起来很简单, 但却不可用. 的单连通区域必定含有奇点E . 又如本节例2, 对任2L L 与因为任何包含2222(,),(,)y x P x y Q x y x y x y-==++只在剔除原点外的任何区域D 上有定义, 含在某个复连通区域内. 的条件, 因而就不能保证(3)式成立. 为绕原点一周的圆:cos ,sin (02π),L x a y a θθθ==≤≤则有倘若L 为绕原点一周的封闭曲线, 则函数这时它不满足定理21.1222d d L x y y x x y -+⎰所以L 必事实上, 若取L 2222220cos sin d a a aπθθθ+=⎰==⎰20d 2.θππ注2 若(,),(,)P x y Q x y 满足定理21.12 的条件, 则由上述证明可看到二元函数(,)(,)d (,)d ABu x y P x y x Q x y y =+⎰00(,)(,)(,)d (,)d B x y A x y P x y x Q x y y=+⎰具有性质d (,)(,)d (,)d .u x y P x y x Q x y y =+我们也称(,)u x y 为d d P x Q y +的一个原函数.例5试应用曲线积分求(2sin )d (cos )d x y x x y y ++的原函数.解这里(,)2sin ,(,)cos ,P x y x y Q x y x y =+=在整个平面上成立cos .P Q y y x ∂∂==∂∂由定理21.12,曲线积分(2sin )d (cos )d ABx y x x y y ++⎰为此, 取(0,0),(,),O B x y 取路线为图21-22中的折只与起点A 和终点B 有关, 而与路线的选择无关.x 2122-图(,0)C x (,)B x y Oy ∙∙∙线段 .OCB00(,)2d cos d x yu x y t t x s s =+⎰⎰2sin .x x y C =++注由例4 可见, 若00[,][,],x x y y D ⨯⊂则求全微分的原函数可用公式于是有或000(,)(,)d (,)d .x y x y u x y P t y t Q x s s =+⎰⎰下例介绍用“凑微分”法求全微分的原函数. 00(,)(,)d (,)d x y x y u x y P t y t Q x s s =+⎰⎰例6 求全微分221sin d sin d x I x y xy x y x xy y y y ⎛⎫⎛⎫=+-+-- ⎪ ⎪⎝⎭⎝⎭的原函数(,).u x y 221sin sin x x y xy y x xy y y x y ⎛⎫⎛⎫∂∂+-=-- ⎪ ⎪∂∂⎝⎭⎝⎭21sin cos ,xy xy xy y=---因此I 是某个函数的全微分. (,)u x y 解由于由221sin d sin d x x y xy x y x xy y y y ⎛⎫⎛⎫+-+-- ⎪ ⎪⎝⎭⎝⎭()()221d d d d sin d sin d x x x y y x y y xy x x xy y y y ⎛⎫=++-+-- ⎪⎝⎭()2311d d d cos 23x x y xy y ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭2311d cos ,23x x y xy y ⎛⎫=+++ ⎪⎝⎭可见2311(,)cos ,23x u x y x y xy C y=++++其中C 为任意常数.复习思考题验证格林公式的另一形式:d d [cos(,)cos(,)]d ,D D P Q x y P n x Q n y s x y ∂⎛⎫∂∂+=+ ⎪∂∂⎝⎭⎰⎰⎰ n D D ∂其中是的边界上任一点处的外法线向量.。