04. 圆轴的扭转解析
- 格式:ppt
- 大小:1.43 MB
- 文档页数:51
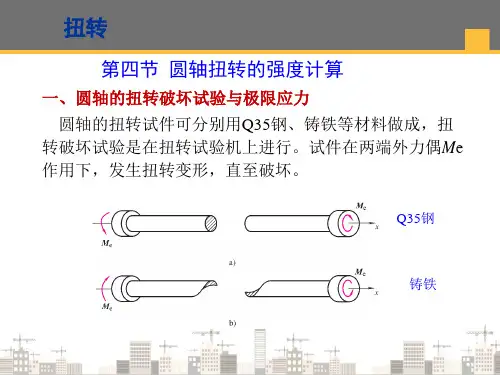

圆轴扭转试验圆轴扭转试验是一种通过给定试样施加扭转力来评估其材料特性的试验方法。
在此试验中,一个圆柱形材料样品以固定位置夹在两个固定的夹具之间。
一端的夹具被固定在试验装置上,而另一端的夹具则被连接到一个旋转的轴上。
在扭转试验期间,扭矩从旋转的轴上施加在试样上,试样随着扭矩旋转,并且测量所施加的扭矩和转角。
圆轴扭转试验可以由多种方式进行。
例如,可以使用电动机或液压系统应用扭矩。
还可以在常温或高温下进行试验。
试验时,需要记录的数据包括扭矩和角度。
扭矩的测量可以通过安装扭矩传感器来实现,而角度的测量通常使用编码器或激光技术来实现。
在对数据的分析中,会计算出材料的切应变和切应力,用于评估材料的特性。
通过圆轴扭转试验,可以评估材料的许多力学特性,例如最大扭转强度、弹性模量、塑性应变、塑性应力以及疲劳特性。
一些特殊的应用也可以使用圆轴扭转试验进行研究,例如涉及高强度材料、高温环境或复合材料的应用。
在准备圆轴扭转试验时,需要注意试样的准备和制备方法。
试样必须均匀且无损,并且必须符合所选择的标准。
一些标准规定了试样的直径、长度以及表面处理等要求。
为了减少试验误差,试样必须正确安装在夹具上,并且轴线必须与夹具轴线对齐。
试样必须夹紧固定,以保证其在试验过程中不会发生移动或旋转。
同时,试验前必须仔细校准仪器,包括扭矩传感器、编码器以及任何其他相关仪器。
在圆轴扭转试验过程中,需要注意试验环境的控制。
例如,在高温环境中进行试验时,需要确保试验室中的温度和湿度稳定,以避免试验结果的误差。
同样,在常温试验中,也需要避免试验室中的振动和其他不稳定的条件,以确保得到准确的试验结果。
总之,圆轴扭转试验是一种有效的评估材料特性的方法。
通过使用准确的仪器和正确的试验技术,可以获得准确的试验结果,并且可以在多种应用中使用。
然而,需要仔细准备试样,并严格控制试验环境,以确保得到准确的结果。

第五节圆轴的扭转变形与刚度条件一、圆周的扭转变形圆轴受扭转时,除了考虑强度条件外,有时还要满足刚度条件。
例如机床的主轴,若扭转变形太大,就会引起剧烈的振动,影响加工工件的质量。
因此还需对轴的扭转变形有所限制。
轴受扭转作用时所产生的变形,是用两横截面之间的相对扭转角ϕ表示的,如下图所示。
由于γ角与ϕ角对应同一段弧长,故有ϕ·R = γ·l (a)式中的R是轴的半径,由剪切虎克定律,τ=G·γ,所以可得ϕ=τ·l/ (G·γ)(b)式中τ=M·R/ Jρ,代入(b)得:ϕ=M·l/ (G·Jρ)(1-46)公式(1-46)是截面A、B之间的相对扭转角计算公式,ϕ的单位是rad。
两截面间的相对扭转角与两截面间的距离l成正比,为了便于比较,工程上一般都用单位轴长上的扭转角θ表示扭转变形的大小:θ=ϕ/ l=M/ (G·Jρ)(1-47)θ的单位是rad/m。
如果扭矩的单位是N·m,G的单位MP a,Jρ的单位m4。
但是工程实际中规定的许用单位扭转角[θ]是以°/m 为单位的,则公式(1-47)可改写为:(1-48)式中G·Jρ称为轴的抗扭刚度,取决于轴的材料与截面的形状与尺寸。
轴的G·Jρ值越大,则扭转角θ越小,表明抗扭转变形的能力越强。
二、扭转的刚度条件圆轴受扭转时如果变形过大,就会影响轴的正常工作。
轴的扭转变形用许用扭转角[θ]来加以限制,其单位为°/m,其数值的大小根据载荷性质、工作条件等确定。
在一般传动和搅拌轴的计算中,可选取[θ]=0.5°/m~10°/m。
由此得出轴的扭转刚度条件:θ=M/ (G·Jρ)·(180/ π)≤[θ](1-49)圆轴设计时,一般要求既满足强度条件(1-45),又要满足刚度条件(1-49)。

圆轴扭转的变形特点是杆件的各横截面绕杆轴线发生相
对转动。
圆轴扭转是指杆件受到扭矩作用时,杆件的各个横截面绕杆轴线发生
相对转动的变形现象。
圆轴扭转具有以下几个特点:
1.存在剪应变分布不均匀性:在圆轴扭转中,由于剪应力随着距离杆
轴线的远近而变化,导致杆件各个横截面上的剪应变分布不均匀。
通常在
杆件的中心位置,剪应力相对较小,而在杆件的边缘位置,剪应力相对较大。
2.具有剪应变相关的线性关系:在圆轴扭转中,剪应变与杆件上施加
的剪应力之间存在线性关系。
这意味着剪应变可以通过剪应力的大小来计
算得到,而且一旦知道了剪应力分布,就可以确定各个截面上的剪应变分布。
3.横截面形状不变:在圆轴扭转中,尽管杆件的各个横截面发生了相
对转动,但是每个横截面的形状并不变化。
这是因为杆件在扭转过程中,
其内部的材料总体上是在沿横截面的切线方向变形,而不是发生形变。
4.通过圆周方向移动点的轨迹是螺旋线:在圆轴扭转过程中,杆件上
的各点在圆周方向的移动轨迹是螺旋线。
这意味着随着扭转角度的增加,
杆件上各点的位移呈螺旋形状,而不是简单的直线位移。
5.与轴向应变相关:圆轴扭转中,轴向应变与剪应变之间存在一定的
关联。
具体来说,当杆件受到扭矩作用时,会引起杆件的轴向长度发生变化,即出现轴向应变。
而轴向应变的大小与剪应变成正比,即剪应变越大,轴向应变也越大。



第八章 圆轴的扭转工程构件一般可分为三类。
第四章已指出:杆是某一方向尺寸远大于其它二方向尺寸的构件,若杆件的轴线为直线,则称为直杆。
此外,若构件在某一方向的尺寸远小于其它二方向的尺寸,称之为板。
若构件在x 、y 、z 三个方向的尺寸具有相同的数量级,则称为块体。
本课程主要讨论直杆,这是一种最简单的构件。
如同4.4节所述,在空间任意力系的作用下,杆件截面内力的最一般情况是六个分量都不为零,其变形是很复杂的。
为了简化讨论,我们将杆的基本变形分成为三类,即拉压、扭转、弯曲,如图4.3所示。
前面已经讨论了在轴向载荷作用下杆的拉伸和压缩;现在再来研究杆的另一类基本变形,即扭转问题。
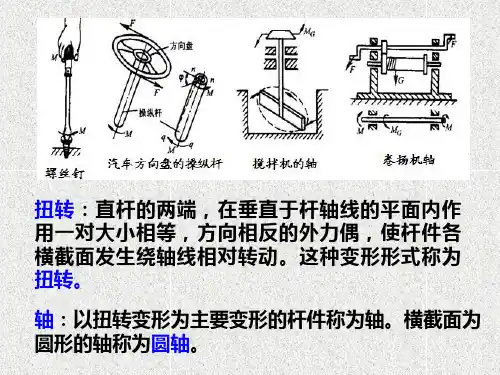
§8.1扭转的概念和实例工程中承受扭转的构件是很常见的。
如图8.1所示的汽车转向轴,驾驶员操纵方向盘将力偶作用于转向轴AB 的上端,转向轴的下端B 则受到来自转向器的阻抗力偶的作用,使转向轴AB 发生扭转。
又如图8.2中的传动轴,轮C 上作用着主动力偶矩,使轴转动;轮D 输出功率,受到阻力偶矩的作用,轴CD 也将发生扭转。
以上二例都是承受扭转的构件实例。
由于工程中承受扭转的构件大多为圆截面直杆,故称之为轴。
本章亦仅限于讨论直圆轴的扭转问题。
图8.2 传动轴图8.3所示为等截面直圆轴扭转问题的示意图。
扭转问题的受力特点是:在各垂直于轴线的平面内承受力偶作用。
如在图8.3中,圆轴AB 段两端垂直于轴线的平面内,各作用有一个外力偶M 0,此二力偶的力偶矩相等而转向相反,故是满足平衡方程的。
圆轴扭转问题的变形特点是:在上述外力偶系的作用下,圆轴各横截面将绕其轴线发生相对转动;任意两横截面间相对转过的角度,称为相对扭转角,以φ表示。
图8.3中,φAB 表示截面B 相对于截面A 的扭转角。
必须指出,工程中的传动轴,除受扭转作用外,往往还伴随有弯曲、拉伸(压缩)等其它形式的变形。
这类问题属于组合变形,将在以后研究。
§8.2 扭矩与扭矩图已知轴所传递的功率、转速,可利用6.3节提供的“功率、转速与传递的扭矩之关系”来计算作用于传动轴上的外力偶矩M 0。


