圆轴扭转时的变形与刚度计算圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
圆轴扭转是指轴材受到扭矩作用产生的变形现象。
在圆轴扭转中，轴材会经历弹性变形和塑性变形。
弹性变形是指轴材在扭矩作用下恢复原状的变形，而塑性变形则是指超过轴材弹性限度后产生的永久变形。
圆轴扭转可通过弹性力学原理进行分析。
根据胡克定律，弹性体的应力与应变之间有线性关系。
对圆轴来说，变形主要体现为轴材的剪切变形。
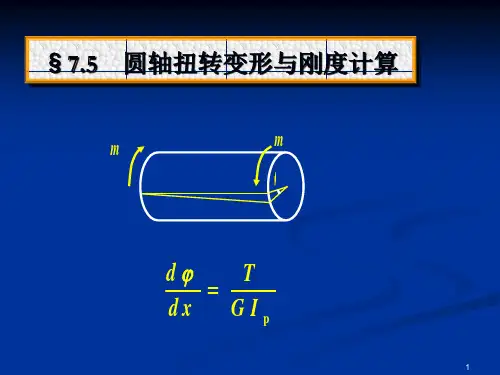
剪切形变角度φ与应力τ之间的关系为：τ=G*φ其中，G是剪切模量，表示材料抵抗剪切变形的能力。
φ是单位长度的圆周上小弧δs扭转对应的形变角。
通过积分可得到实际的扭转角θ与应力之间的关系：τ=G*θ/L其中，L是轴材的长度。
对于圆轴来说，扭转力矩T与应力分布之间的关系为：T=τ*A其中，A是轴材的横截面积。
将τ带入等式可得到扭转角与扭转力矩之间的关系：T=G*θ*A/L从上述公式可知，轴材扭转角度与扭转力矩之间存在一线性关系，即扭转刚度k。
k=G*A/L通过上述公式，可以得到轴材的扭转刚度。
扭转刚度越大，则轴材对于扭转力矩的抵抗能力越强。
此外，圆轴扭转时的变形也与材料的断裂强度有关。
当扭转力矩超过材料的断裂强度时，轴材会发生塑性变形，产生永久变形。
在实际应用中，通常会根据所需要的刚度和工作条件来选择合适的轴材及其横截面积。
在计算中需要考虑到轴材的材料特性、几何形状和所受的载荷等因素。
此外，还可以通过模拟实验或数值计算的方法对扭转变形和刚度进行验证和评估。
总之，圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
通过弹性力学原理，可以分析轴材在扭转力矩作用下的变形情况，并计算出轴材的扭转刚度。
这对于轴类零件的设计和工程应用具有重要意义。
