4-4高阶微商与高阶微分

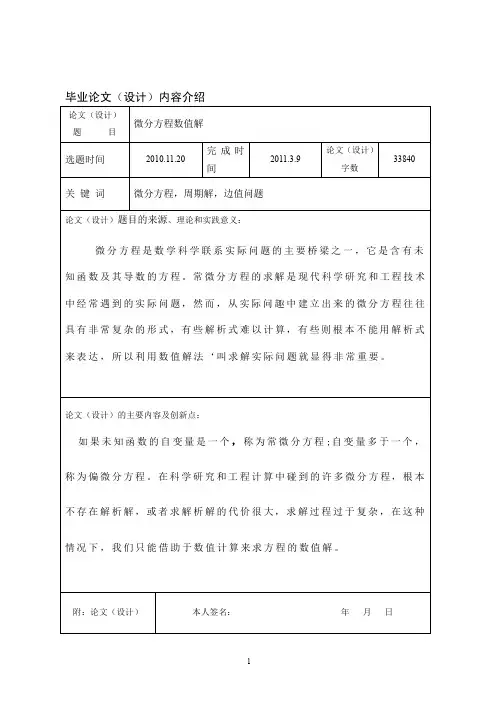
毕业论文（设计）内容介绍论文（设计）题目微分方程数值解选题时间2010.11.20完成时间2011.3.9论文（设计）字数33840关键词微分方程，周期解，边值问题论文（设计）题目的来源、理论和实践意义：微分方程是数学科学联系实际问题的主要桥梁之一，它是含有未知函数及其导数的方程。

常微分方程的求解是现代科学研究和工程技术中经常遇到的实际问题，然而，从实际问趣中建立出来的微分方程往往具有非常复杂的形式，有些解析式难以计算，有些则根本不能用解析式来表达，所以利用数值解法‘叫求解实际问题就显得非常重要。

论文（设计）的主要内容及创新点：如果未知函数的自变量是一个，称为常微分方程;自变量多于一个，称为偏微分方程。

在科学研究和工程计算中碰到的许多微分方程，根本不存在解析解，或者求解析解的代价很大，求解过程过于复杂，在这种情况下，我们只能借助于数值计算来求方程的数值解。

附：论文（设计）本人签名：年月日目录中文摘要 (5)第一章常微分方程的解 (6)第一节常微分方程的基本概念 (6)第二节常微分方程的12步骤 (10)第三节偏导数的方程 (14)第二章递增方程的应用 (17)第一节递增数列 (17)第二节数列的极限 (20)第三章与积分有关的数列的极限问题 (24)第一节积分的应用 (24)第二节单调定性的松弛法 (26)第三节松弛算法法的证明 (33)第四章简单的单步法及基本概念 (36)第一节解初值问题的梯形法 (36)第二节左矩形公式 (39)第三节隐式Euler方法 (40)第四节预估–校正Euler方法 (42)参考文献 (45)摘要：常微分方程的形成和发展是与力学、天文学、物理学及其他自然科学技术的发展互相促进和互相推动的。

本文第一章讲述了常微分方程的发展历史，第二章介绍了一系列常微分方程的周期解和边值问题，说明了其研究现状，第三章举例说明了其在生态学和军事上的应用。

无论在数学研究还是在自然科学以及其他应用科学，常微分方程都显现出其重要的理论和应用价值。

§4 高阶微商与高阶微分1．高阶微商物体运动规律)(t S 瞬时速度 ()v t ＝()s t '＝ds dt瞬时加速度 ()a t ＝()v t '＝(())s t ''，或 ()a t ＝dvdt＝()d ds dt dt ． 由此产生了高阶导数的概念．一般地，设()y f x =在(,)a b 可导，则()f x '仍是(,)a b 上的函数．若()f x '也在(,)a b 可导，则称()f x '的微商(())f x ''为()f x 的二阶微商(二阶导数)，记为()f x ''或(2)()fx 或22d ydx类似地可定义()f x ''的微商为()f x 的三阶微商(三阶导数)，记为 ()f x '''或(3)()fx 或33d y dx．定义(1)()n f x -的微商为()f x 的n 阶微商(n 阶导数)，记为 ()()n f x 或n n d ydx＝11()n n d d y dx dx --．下面给出几个常用的n 阶导公式 例1例2 设sin y x =，求()n y解 'c o s y x =，''s i n y x =-，'''c o s y x =-，(4)y s i n x =。

设n y x = (n 是正整数)，若n k ≤，则 k n k x k n n n y -+--=)1()1()( 若n k >，则 0)(=k y研究规律，得 'c o s y x =s i n ()2x π=+，''y =cos()2x π+＝sin()22x ππ++＝2sin()2x π+，'''y =2cos()2x π+＝2sin()22x ππ++＝3sin()2x π+由此我们不难归纳出对于cos y x =，则 c o s s i n ()2y x x π==+()n y =sin()22n x ππ++cos()2n x π=+例3 设arctan y x =，求()n y 解 21'1y x=+211t a n y =+2c o s y =； 方程两边再对x 求导并注意y 是x 的函数，得 =-='⋅-=''y y y y y y 2cos 2sin sin cos 22cos y sin 2(2y π+)；2'''[2c o s s i n s i n 2()2c o s 2()c o s ]'22y y y y y y y ππ=-+++32c o s [c o s 2()c o s s i n s i n 2()]22y y y yy ππ=+-+ )3c o s (c o s 23π+=y y ＝332c o s s i n (3)2y y π+)2(3s i nc o s 23π+=y y ； 若()(1)!cos sin ()2n n y n y n y π=-+，则x y sin =()n y = sin()2n x π+ x y cos = )(n y cos()2n x π=+(1)n y +1(1)![c o ss i n s i n ()c o s c o s ()]'22n nn n y y n y ny n y y ππ-=--+++1()!cos [cos cos ()sin sin ()]22n n y y n y y n y ππ+=+-+1!cos cos[(1)]2n nn y n y π+=++1!cos sin(1)()2n n y n y π+=++由数学归纳法得例4高阶微商的运算法则：若,u v 都是x 的函数 1、 ()()n u v ±＝()n u ()n v ±． 2、若v u y ⋅=，则()n y ＝()()nk n k k nk C u v -=∑，n ＝1，2…． （莱布尼兹公式） 这里，函数的零阶导数理解为函数本身．下面用数学归纳法证明．事实上，1=n 时就是导数的乘积公式，设公式对n 成立，则 (1)()()0()'nn kn k k n k yC u v +-==∑ (1)()()(1)0[]n kn k k n k k nk C u v u v -+-+==+∑ arctan y x =()n y ＝(1)!cos sin ()2n n y n y π-+xy 1=1)(!)1(+-=n nn x n y(1)()()(1)nnk n k k k n k k nn k k C uvC u v -+-+===+∑∑ （令j k =+1） 1(1)()1(1)()1nn kn k k k n k k nn k k C uvC u v +-+-+-===+∑∑ 0(1)(0)1(1)()(0)(1)1()nn k k n k k n n nn n n k C uvC C u v C u v +--++==+++∑ 1(1)()10n k n k k n k C uv +-++==∑ 其中用等式 001n n C C +=，11n n n n C C ++=， kn k nk n C C C 11+-=+ 由数学归纳法知公式对一切正整数n 成立。

大学微积分l 知识点总结第一部分大学阶段准备知识 1、不等式：ab 2ba ≥+2121n n 2211......a a b a ...b a b a n n b b b a +++++≤+++()时取等号为常数，当且仅当，n ...3,2,1i b a i i ==λλ2、函数周期性和对称性的常用结论1、若fx+a=±fx+b,则fx 具有周期性；若fa+x=±fb-x,则fx 具有对称性; 口诀：“内同表示周期性,内反表示对称性”2、周期性1若fx+a=fb+x,则T=|b-a| 2若fx+a=-fb+x,则T=2|b-a| 3若fx+a=±1/fx,则T=2a 4若fx+a=1-fx/1+fx,则T=2a 5若fx+a=1+fx/1-fx,则T=4al n sin =∂正弦 l m cos =∂余弦 m ntan =∂正切n m cot =∂余切 m l sec =∂正割 n lcsc =∂余割∂=∂cot 1tan ∂=∂csc 1sin ∂=∂sec 1cos商的关系：∂∂=∂=∂∂csc sec tan cos sin ∂∂=∂=∂∂sec csc cot sin cos平方关系：()()sina cosa 1cosa-1sina 2a cot sina cosa -1cosa 1sina 2a tan cosa 1212a cos cosa -1212a sin 22+==⎪⎭⎫⎝⎛=+=⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛•⎪⎭⎫ ⎝⎛+•=⎪⎭⎫⎝⎛•⎪⎭⎫ ⎝⎛+•=⎪⎭⎫⎝⎛•⎪⎭⎫ ⎝⎛+•=a -3tan a 3tan tana a 3tan a -3cos a 3cos cosa 4a 3cos a -3sin a 3sin sina 4a 3sin ππππππ 万能公式：()ββtan tan 1-tan •∂+=∂和差化积公式：()()⎦⎤⎢⎣⎡⎦⎤⎢⎣⎡+=+21-cos 21sin 2sin sin ϕθϕθϕθ()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=21-sin 21cos 2sin -sin ϕθϕθϕθ ()()⎥⎦⎤⎢⎣⎡⎦⎤⎢⎣⎡+=+21-cos 21cos 2cos cos ϕθϕθϕθ ()()()⎥⎦⎤⎢⎣⎡⎦⎤⎢⎣⎡+=21-sin 21sin 2-cos -cos ϕθϕθϕθ原式得证，由题，22b a x x cos x sin 1x x +=∴===⎪⎭ ⎝+⎪⎭ ⎝M M 4、数学归纳法数学上证明与自然数N 有关的命题的一种特殊方法,它主要用来研究与正整数有关的数学问题,在高中数学中常用来证明等式成立和数列通项公式成立;例如：前n个奇数的总和是n2,那么前n个偶数的总和是：n2+n最简单和最常见的数学归纳法证明方法是证明当n属于所有正整数时一个表达式成立,这种方法由下面两步组成：①递推的基础：证明当n=1时表达式成立②递推的依据：证明如果当n=m时成立,那么当n=m+1时同样成立1第一数学归纳法5、初等函数的含义概念：初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数与常数经过有限次的有理运算以及有限次数函数复合所产生,并且能用一个解析式表示的函数;有理运算：加、减、乘、除、有理数次乘方、有理数次开方基本初等函数：对数函数、指数函数、幂函数、三角函数、反三角函数6、二项式定理：即二项展开式,即a+b n 的展开式()nn n k k -n k n 1-n 1n n 0n n b ...b a ...b a a C b a C C C ++•++•+=+称为二次项系数其中kn C表示项，用项，它是第叫做二次项展开式的通1k k k -n kn 1k b a ++•T Cn n y∞→8、其他一些知识点10不是正数,不是负数;是自然数;0是偶数,偶数分为：正偶数、负偶数和0 （2）正偶数称为“双数” （3）正常数：常数中的正数（4）质数：又称“素数”;一个大于1的自然数,如果除了1和它自身以外,不能被其他自然数整除的数,否则称为“合数”;最小的质素数是2;1既不是素数,也不是合数;（5）exp ：高等数学中,以自然对数e 为底的指数函数 （6）在数学符号中,sup 表示上界；inf 表示下界 （7）≡：表示恒等于（8）0的阶乘是1.阶乘是一个递推定义,递推公式为：n=nn-1因为1的阶乘为其中,e n 11n→⎪⎭⎫⎝⎛+,e 为初等函数,又称“幂指函数”,e 即根据此公式得到,e ≈2.7181n 1-1n2→⎪⎭⎫⎝⎛ ()()61n 21n n n ...21222++=+++()233321n n n ...21⎥⎦⎤⎢⎣⎡+=+++()1-a a-a s a ...a a s 1n n 2+=+++=()()()()()1-n 2-n 1-n n n b ...b a a b -a b -a +++=x sinx 0x →→时， x tanx → 2x 21cosx -1→列举一些趋向于0的函数：()0lnn 10n a 1a 0c -n b0b 0a 0q 1q b nan →→→→④，＞③，＞，＞②，＜①柯西极限存在准则：3斯托尔茨定理设数列n y 单调增加到无穷大,则11lim lim--∞→∞→--=n n n n n n n n y y x x y x ()[]()a x g f x g f x f x x x x =⎥⎦⎤⎢⎣⎡=→→00lim lim )().4(是连续函数：如：nn n S S n S --++++=-2232 (2523211)32n 解题思路： 函数的连续性和间断点问题 1如何讨论并确定函数的连续性①若该函数是初等函数,则该函数在其定义域区间均连续②若是一元函数,则可对其求导,其导数在某点上有意义则函数在该点必然连续的x f x )()0=00)''()'(''''''00x )('''x x )()''()'(''''''0.0x )(εδδεεδεδε≥----∈∃∀x f x f x x x x x f x x x f x f x f x x x x x x f ，但是＜，尽管、存在，总＞，无论对多么小的＞上，存在定义在集合不一致连续：设函数小。

第四章 微商与微分
一、学习要求：
（1）正确理解微商的概念；
（2）知道微商的几何意义与物理意义；
（3）掌握可导与连续的关系；
（4）牢固掌握求导的四则运算公式、复合函数求导的法则和反函数求导的法则，能迅速正确地求初等函数的导数；
（5）熟悉基本初等函数的求导公式；
（6）掌握隐函数的求导法，对数求导法，由参数方程确定的函数的求导法；
（7）正确理解微分概念；
（8）了解可微与可导的关系，知道导数与微分的区别与联系；
（9）正确理解一阶微分的形式不变性，并会用它求导．
二、学习的重点与难点
重点：微商与微分的概念，求导的四则运算法则，复合函数的求导法则，基本
初等函数的求导公式．
难点：复合函数的求导法则，一阶微分的形式不变性．
三、导数的常用计算方法
（1）利用微商的定义求导；
（2）利用求导的四则运算法则及基本初等函数的导数公式求导；
（3）利用反函数求导法则求导；
（4）利用复合函数的链式法则求导；
（5）利用对数求导法则求导；
（6）隐函数求导法；
（7）由参数方程给出的函数的求导；
（8）用莱布尼兹公式求高阶导数．
四、微分的求法
（1）用()dx x f dy '=来求；
（2）利用微分的四则运算公式来求；
（3）利用一阶微分的形式不变性来求复合函数的微分．。

第四章 微商与微分概念清楚，运算熟练与准确，是本章的基本要求．微分是函数改变量的线性主部,常用来做近似计算.数值上等于导数与自变量改变量的乘积.微商也叫导数,是函数改变量与自变量改变量的比的极限,描述函数的变化率.可以理解为微分之商.其几何意义是函数图像切线的斜率.物理意义是即时速度,即时加速度等.设函数y = f(x)在x 0的邻域内有定义，x 0及x 0 + Δx 在此区间内。

如果函数的增量Δy = f(x 0 + Δx) - f(x 0)可表示为 Δy = AΔx + o(Δx)（其中A 是不依赖于Δx 的常数），而o(Δx)是比Δx 高阶的无穷小（注：o 读作奥密克戎，希腊字母）那么称函数f(x)在点x 0是可微的，且AΔx 称作函数在点x 0相应于自变量增量Δx 的微分，记作dy ，即dy = AΔx 。

函数的微分是函数增量的主要部分，且是Δx 的线性函数，故说函数的微分是函数增量的线性主部（△x→0）。

[1]通常把自变量x 的增量 Δx 称为自变量的微分，记作dx ，即dx = Δx 。

于是函数y = f(x)的微分又可记作dy = f'(x)dx 。

函数的微分与自变量的微分之商等于该函数的导数。

因此，导数也叫做微商。

§1 微商概念及其计算1．微商概念例1 质点作变速直线运动的瞬时速度．当自变量X 改变设质点P 沿直线作变速运动，运动规律 )(t S S =， 问题：求质点P 在时刻0t 的瞬时速度0()v t ．从0t 到t t ∆+0一段时间内，质点P 所走过的路程为 )()()(000t S t t S t S -∆+=∆平均速度为 tt S t t S t S v ∆-∆+=∆∆=)()(00Word2007中，这是页面背景问题，分情况处理。

方法如下：单文字有阴影，简单方法是选中有阴影的文字，单击“开始”中带底纹的A 字就可以去掉底纹了。

段落（编辑区）有阴影，选中段落文字，进行下列操作：单击“页面布局”、“页面背景”中的“页面边框”、边框和底纹、底纹（填充：无颜色、应用于：段落。

§5 微 分[教学目的] （1）准确掌握微分的概念，明确其几何意义,能从定义出发求一些简单函数的导数与微分。

（2)弄清可导与可微之间的一致及其相互关系，熟悉微分的运动性质和微分法则，牢记基本的初等函数的微分公式，并熟练进行初等函数的微分运算.（3）能利用微分的几何意义等解决一些实际应用的计算问题.［教学要求］(1）清楚地理解函数在一点的微分的定义，并给出其几何解释；能从定义出发求某些简单函数的微分、能熟练运用基本微分表和微分运算公式求初等函数的微分。

（2)明确函数在一点可导性与一点可微之间的一致性，并会利用导数为微分、利用微分求导数.会应用微分的实际意义解决某些计算问题。

［教学重点］ 微分的定义、计算、可导与可微的关系[教学难点] 运用微分的意义解决实际问题一、微分的概念1．引言先考察一个具体的问题，推得一般情形。

2．微分的定义定义1 函数y=f(x)定义在点0x 的某邻域0()u x 内。

当给0x 一个增量x ∆，00()x x U x +∆∈时，相应地得到函数的增量为00()()y f x x f x ∆=+∆-。

如果存在常数A ，使得y ∆能有()y A x o x ∆=∆+∆ (1)则称函数f 在点0x 可微，并称(1）中右端第一项A x ∆为f 在点0x 的微分，记作：0x x dy A x ==∆ or 0()x x df x A x ==∆定义2 若y=f(x)在区间I 上每一点都可微，则称f 为I 上的可微函数.函数y=f(x)在I 上任一点x 处的微分记作()dy A x x =∆ x I ∈注 （1)dy 依赖于x 和x ∆，但x 与x ∆无关；（2）可微与可导的关系见下面的定理。

定理1 函数f 在点0x 可微⇔f 在点0x 可导，而且0()A f x '=.（3）当函数为y=x ，一方面dy dx =,另一方面dy A x x =∆=∆，因此我们可得微分dy A x =∆,以后记作：dy Adx =;（4）对可导函数y ＝f(x),其微分为()dy A x Adx f x dx '=∆==.例：()()x x x d e e dx e dx '==；22()()2d x x dx xdx '==；(sin )(sin )cos d x x dx xdx '==（5）对可导函数y=f(x)，有()dy f x dx '=，从而有()dy f x dx'=，即函数的导数是函数微分与自变量微分的商（导数即微商）。

§4 高阶微商与高阶微分1．高阶微商物体运动规律)(t S 瞬时速度 ()v t ＝()s t '＝ds dt瞬时加速度 ()a t ＝()v t '＝(())s t ''，或 ()a t ＝dvdt＝()d ds dt dt ． 由此产生了高阶导数的概念．一般地，设()y f x =在(,)a b 可导，则()f x '仍是(,)a b 上的函数．若()f x '也在(,)a b 可导，则称()f x '的微商(())f x ''为()f x 的二阶微商(二阶导数)，记为()f x ''或(2)()fx 或22d ydx类似地可定义()f x ''的微商为()f x 的三阶微商(三阶导数)，记为 ()f x '''或(3)()fx 或33d y dx．定义(1)()n f x -的微商为()f x 的n 阶微商(n 阶导数)，记为 ()()n f x 或n n d ydx＝11()n n d d y dx dx --．下面给出几个常用的n 阶导公式 例1例2 设sin y x =，求()n y解 'c o s y x =，''s i n y x =-，'''c o s y x =-，(4)y s i n x =。

设n y x = (n 是正整数)，若n k ≤，则 k n k x k n n n y -+--=)1()1()( 若n k >，则 0)(=k y研究规律，得 'c o s y x =s i n ()2x π=+，''y =cos()2x π+＝sin()22x ππ++＝2sin()2x π+，'''y =2cos()2x π+＝2sin()22x ππ++＝3sin()2x π+由此我们不难归纳出对于cos y x =，则 c o s s i n ()2y x x π==+()n y =sin()22n x ππ++cos()2n x π=+例3 设arctan y x =，求()n y 解 21'1y x=+211t a n y =+2c o s y =； 方程两边再对x 求导并注意y 是x 的函数，得 =-='⋅-=''y y y y y y 2cos 2sin sin cos 22cos y sin 2(2y π+)；2'''[2c o s s i n s i n 2()2c o s 2()c o s ]'22y y y y y y y ππ=-+++32c o s [c o s 2()c o s s i n s i n 2()]22y y y yy ππ=+-+ )3c o s (c o s 23π+=y y ＝332c o s s i n (3)2y y π+)2(3s i nc o s 23π+=y y ； 若()(1)!cos sin ()2n n y n y n y π=-+，则x y sin =()n y = sin()2n x π+ x y cos = )(n y cos()2n x π=+(1)n y +1(1)![c o ss i n s i n ()c o s c o s ()]'22n nn n y y n y ny n y y ππ-=--+++1()!cos [cos cos ()sin sin ()]22n n y y n y y n y ππ+=+-+1!cos cos[(1)]2n nn y n y π+=++1!cos sin(1)()2n n y n y π+=++由数学归纳法得例4高阶微商的运算法则：若,u v 都是x 的函数 1、 ()()n u v ±＝()n u ()n v ±． 2、若v u y ⋅=，则()n y ＝()()nk n k k nk C u v -=∑，n ＝1，2…． （莱布尼兹公式） 这里，函数的零阶导数理解为函数本身．下面用数学归纳法证明．事实上，1=n 时就是导数的乘积公式，设公式对n 成立，则 (1)()()0()'nn kn k k n k yC u v +-==∑ (1)()()(1)0[]n kn k k n k k nk C u v u v -+-+==+∑ arctan y x =()n y ＝(1)!cos sin ()2n n y n y π-+xy 1=1)(!)1(+-=n nn x n y(1)()()(1)nnk n k k k n k k nn k k C uvC u v -+-+===+∑∑ （令j k =+1） 1(1)()1(1)()1nn kn k k k n k k nn k k C uvC u v +-+-+-===+∑∑ 0(1)(0)1(1)()(0)(1)1()nn k k n k k n n nn n n k C uvC C u v C u v +--++==+++∑ 1(1)()10n k n k k n k C uv +-++==∑ 其中用等式 001n n C C +=，11n n n n C C ++=， kn k nk n C C C 11+-=+ 由数学归纳法知公式对一切正整数n 成立。

高阶无穷小微分高阶无穷小微分是微积分中的一个重要概念，它在数学和物理学等领域中起着至关重要的作用。

它是微积分中的一个工具，用来描述函数在某一点附近的行为。

它可以帮助我们更好地理解和分析各种变化过程，并解决一些复杂的问题。

在微积分中，我们常常会遇到函数在某一点附近的变化情况。

通常情况下，我们可以通过一阶导数来描述函数的变化率。

但是，在某些情况下，一阶导数无法完全描述函数的变化，这时候就需要引入高阶无穷小微分。

高阶无穷小微分可以看作是一阶导数的推广。

它通过求取函数在某一点附近的高阶导数来描述函数的变化情况。

具体来说，高阶无穷小微分可以用来描述函数在某一点附近的曲率、凹凸性以及高阶变化情况等。

在实际应用中，高阶无穷小微分可以用来解决一些复杂的问题。

比如，在物理学中，我们常常需要研究物体的运动情况。

通过求取物体位置函数的高阶无穷小微分，我们可以得到物体的速度、加速度以及其他相关信息。

这些信息对于研究物体的运动轨迹和行为变化非常重要。

在工程学中，高阶无穷小微分也有着广泛的应用。

比如，在控制系统中，我们常常需要研究系统的稳定性和响应速度。

通过求取系统传递函数的高阶无穷小微分，我们可以判断系统的稳定性，并设计出合适的控制策略。

除此之外，高阶无穷小微分还在其他领域中有着广泛的应用。

比如，在经济学中，我们可以利用高阶无穷小微分来研究经济变量的变化情况；在生物学中，我们可以利用高阶无穷小微分来研究生物体的生长和变化过程。

高阶无穷小微分是微积分中的一个重要概念，它可以帮助我们更好地理解和分析各种变化过程，并解决一些复杂的问题。

它在数学、物理学、工程学等领域中都有着广泛的应用。

通过深入理解和掌握高阶无穷小微分，我们可以更好地应用它来解决实际问题，推动科学技术的发展。