科学计数法导学案

青岛版七年级数学下14.3科学计数法导学案学习目标：知识与技能1.会用科学记数法表示绝对值小于1的数.2.会把一个科学记数法表示的数写成小数形式.过程与方法经历把一个绝对值小于1的非零数表示成科学记数法±a×10n形式（其中1≤a＜10,n为负整数）的过程，发现规律，培养和增强数感.情感态度和价值观体会科学记数法方便、快捷，便于计算的优点.学习过程：一、回顾& 思考：把下列问题中的数据用科学记数法表示.•(1)第五次人口普查时，中国人口约为1300000000人•(2)地球半径约为696000000米．•(3)光的速度约为300000000米/秒•(4)据世界能源会议统计，世界已探明可采煤炭储量共计107539亿吨二、探索：（一）探究点1：用科学记数法表示绝对值小于1的非零数概括（）对应训练1：1.用科学记数法表示0.0000907得（）A.9.07×10-4B.9.07×10-5C.90.7×10-6D.90.7×10-72.下列各数，属于科学记数法表示的有( )A -2×10-2 B. 0.12×103 C. 12.3×10-4 D. 514×10-24. 用科学记数法表示（1）0.00096=（2）-0.006983=（二）探究点2：把科学记数法表示的数化为原数•典例剖析：例：下列用科学记数法表示的数，原数各是多少？（1）-3.14×10-5 （2）9.21×10-3对应训练2：1.用小数表示3×10-2结果是（）A.-0.003B.-0.0003C.0.03D.0.0032. 2.12×10-3写成小数形式为（）A.2120B.212000C.0.00212D.0.0002123.列用科学记数法表示的数，原数各是什么数？（1）8.32×10-5= （2）-6.06×10-6=三、学以致用：1.安哥拉长毛兔最细的兔毛直径约为5×10-6米，将这个数写成小数的形式 。

科学计数法导学案学习目标：了解科学记数法的意义。

借助身边熟悉的事物进一步体会大数，并会用科学记数法表示大数。

学习重难点：重点：能用科学记数法表示大数。

难点：对科学记数法法则的理解。

学法指导：交流讨论，归纳类比教学过程：一、情境引入：1、你能列举生活中的较大数据吗？与同学交流2、请同学们看下面的问题（a）2008年北京奥运会体育场——“鸟巢”能容纳91 000位观众。

(b) 2008年5月12日，在我国四川省汶川县发生里氏8.0级强烈地震，面对地震灾难，各级政府共投入抗震救灾资金22 600 000 000元人民币。

(c) 台风云娜的登陆给温州人民造成的经济损失超过100亿元从上面的问题中，你发现这些数据有什么特点？3.102＝ 104＝ 108＝ 1010=______4.讨论：指数与运算结果中的0的个数有什么关系？与运算结果的数位有什么关系？5.一般地，10的n（为正整数）次幂，在1的后面有个06.3500 = 3.5×_______ 91 000 = 9.1×_____22 600 000 = 2.2 × ________________________二、合作探究1.科学记数法：一个大于10的数可以表示成( ) 的形式，其中1≤a ＜10，n 是正整数，这种记数方法叫做科学记数法。

2.想一想：用科学计数法表示一个大于10的数，10的次数n 与原数的整数位数有何关系？用科学计数法计数有何优点？三、拓展创新例题探究：例1.下列各数用科学记数法表示（1）6 900= （2）-57 000 000=（3）123 000 000 000= (4)1300000000＝例2.下列科学记数法表示的数的原数是什么？（1）3.4×104 = （2）6×105= 思考：原数整数的位数与10的次数n 有什么关系？例3. 二十一世纪，纳米技术将被广泛应用。

纳米是长度计量单位。

《1.5.2科学计数法》课型：新授时间：：学习目标:1.能用科学记数法表示绝对值较大的数。

2.经历运用科学记数法表示一些大数的过程，建立初步的数感和符号感，发展抽象思维的能力；3.借助身边熟悉的事物进一步体会大数，并能用科学记数法表示，发展应用意识。

学习过程1、创设情境，导入新课1）．在日常生活中我们经常遇到的一些较大的数，如：①太阳的半径约696 000千米；②光的速度大约是300 000 000米/秒；③全世界人口数大约是7000 000 000；④应对金融危机，国家计划4年内拨款4000000000000元刺激国内经济。

请同学们读出这些句子？这样的大数（天文数字），读、写都不方便！能否用我们学过的知识简单表示呢？2、新授（复习乘方内容，幂，指数，底数）1）．观察10的乘方有如下的特点：计算：102，103，104，105… …10n；解：102=_______， 103＝________， 104＝________， 105＝________，……10n＝________。

(n为正整数)⑴ 350=3.5×( )=3.5×10( )⑵ 5700=5.7×( )= 5.7×10( )⑶ 65000=6.5×( )= 6.5×10( ) ⑷ 12000=1.2×( )= 1.2×10( )例:把 567 000 000表示成上面相同的形式为:例:1300000000，300000000怎么表示，并说出怎么读？1300000000=_____ ______; 300000000=____ _______.结论：像上面这样，把一个较大的数表示成10na ⨯的形式（其中a 是整数数位只有一位的数，n 为正整数），这种记数法叫做科学记数法.4、用科学记数法记出下列各数:(1)1 000 00(2)57 000 000(3)123 000 000 000⑷56420000万5、巩固练习1）．用科学记数法表示下列各数：（1）351500；（2）10300000；（3）210800 。

课题：《科学计数法导学案》师生札记编写人：七年级阳光部黄婿第一课时【学习目标】1、能将一个有理数用科学记数法表示2、己知用科学记数法表示的数，写出原来的数3、懂得用科学记数法表示数的好处【重点难点】1、用科学记数法表示绝对值大于10的数2、正确使用科学记数法表示数【学法指导】独立自学，以题质疑，探讨解疑，体会运用【知识链接】我们看下面几个数据.(1)第五次人口普查时，中国人曰约为1300000000人.(2)地球半径约为696000000米.(3)光的速度约为300000000米/秒(4)地球离太阳约有1亿五千万千米.(5)地球上煤的储量估计15万亿吨以上这些大数的读、写都有一定困难。

那么可以用怎样的方法来表示这些大数，使它易读、易记、易判断大小还便于计算呢？【自学指导、合作探究】一、自学指导(温馨提示：独立思考，相信聪明的你一定能出色完成下列任务！) 自学1、我们注意到上面这几个数比100万还大.我们知道生活中比100万大的数还很多.但我们发现要表示这些较大的数非常麻烦.例如(5)中15万亿吨=15000000000000吨，这些较大的数写起来很麻烦，有没有简单的表示方法呢？师生札记10=10X10X10=1000;10=10X10X10X 10=10000;10〃 =10xl0xl0x..・xl0 = 1000・・・000 （〃为正整数）、一/ t J〃个10 〃个o你能发现什么规律呢？自学2、填空%1208二 X 二 (整数位有个，指数n=)%12000二2 X 二 (整数位有个,指数n二)%112000=X 二 (整数位有个，指数n二)观察规律：用科学计数法表示一个大于10的数，10的次数n比原数的整数位数________二合作探究探究1、用科学记数法表示下列各数：(1 ) 465000= ( 2) 1200 万二(3) 1000. 001= ( 4) -789=(5) 308X 10』(6) 0.7805X 10’°=探究2、写出下列用科学记数法表示的原数：(1 ) 8. 848X 103= ( 2) 3. 021 X 102=(3) 3X10』(4) 7.5X10,二探究 3 、 1.整数数位从个位起向左依次，，，，>，，(乙，> 。

2.用科学计数法表示下列数字：-0.000 000 819=
3．用四舍五入法按要求对0.05019取近似值，其中错误的是（）
A．0.1（精确到0.1）B．0.05（精确到百分位）
C．0.05（保留两个有效数字）D．0.0502（精确到0.0001）
4.由四舍五入法得到的近似数3.20×10-3有个有效数字，精确到位。
【学习小结】
活动预设
【导入】
【自主学习】
【小组交流】
【展示点拨】
1.归纳：a×10-n
中n为
观察发现：1的前面有n个零
【小结】
《科学计数法》导学案
主备:李梅新审阅;
《科学计数法》学案
【学习目标】
1.理解科学计数法的意义。
2.会用科学计数法表示一些绝对值较小的数。
【导入】
1.将下列各数用科学计数法表示：（1）12亿（2）3020000
【问题导学】
一、阅读课本20页最后两段，完成下列各题。
1.用科学计数法表示一些绝对值较大的数，即利用10的正整指数幂，把的数表示成的形式，其中n是，
≤│α│<
2.我们可以利用10的，用科学计数法表示一些绝对值较小的数，即将它们表示成的形式，其中n是，
≤│α│<
二、应用科学计数法
1.用科学计数法表示下列各数：0.1=
0.0：
0.000 112=
-0.000 0314=
【达标测试】
1.课本练习2、3题。

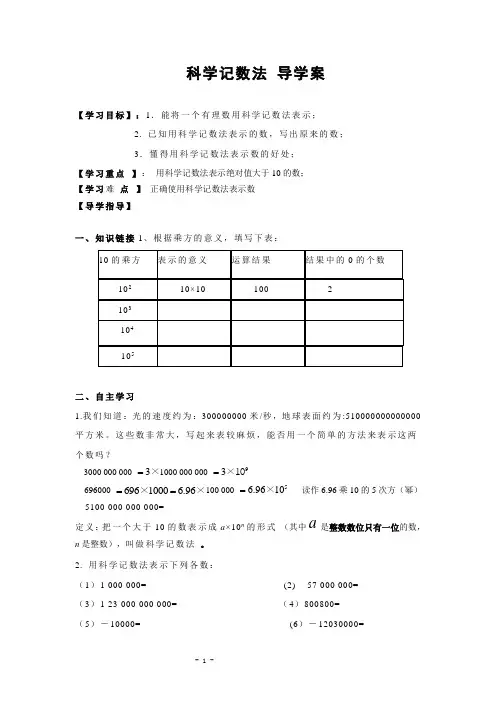
科学记数法 导学案【学习目标】：1．能将一个有理数用科学记数法表示；2. 已知用科学记数法表示的数，写出原来的数； 3．懂得用科学记数法表示数的好处；【学习重点 】： 用科学记数法表示绝对值大于10的数； 【学习难 点 】 正确使用科学记数法表示数 【导学指导】一、知识链接1、根据乘方的意义，填写下表：10的乘方表示的意义运算结果结果中的0的个数102 10×10 100 2 103 104 105二、自主学习1.我们知道：光的速度约为：300000000米/秒，地球表面约为:510000000000000平方米。

这些数非常大，写起来表较麻烦，能否用一个简单的方法来表示这两个数吗？3000 000 000 3=×1000 000 000 93=×10696000 6961000 6.96==××100 000 56.9610=× 读作6.96乘10的5次方（幂） 5100 000 000 000=定义：把一个大于10的数表示成a ×10n 的形式 （其中a 是整数数位只有一位的数，n 是整数），叫做科学记数法 。

2. 用科学记数法表示下列各数：（1）1 000 000= (2) 57 000 000=（3）1 23 000 000 000= （4）800800= （5）－10000= (6）－12030000=归纳：用科学记数法表示一个n 位整数时，10的指数比原来的整数位______三、学以致用：1、下列各数，属于科学记数法表示的是 。

A 、53.7210× B 、0.537410× C 、537210× D 、5.37310× 2、用科学记数法表示下列各数：1000 000； 572 000 000； 30900000-； 2887.6-3、第五次人口普查知山西省人口总数约为3297万人，用科学记数法表示是多少人？4．写出下列用科学记数法表示的原数：（1）8．848×103 （2）3.021×102 （3）3×106 （4）7.5×105四【要点归纳】1什么是科学记数法？ 2 用科学记数法表示一个如何确定a 与n ?五【课堂训练】1．用科学记数法表示下列各数：（1）465000= （2）1200万= （3）1000.001= （4）－789= （5）308×106= （6）0.7805×1010= 2、下列用科学记数法写出的数，原数分别是什么数？7110× 4.5610× 7.04510× 3.96410× 7400-510× 3、在比例尺为1：8000 000的地图上，量得太原到北京的距离为6.4㎝，将实际距离用科学记数法表示为 ㎞。

科学记数法导学案
姓名：学号：
【学习目标】：
1．能将一个有理数用科学记数法表示；
2. 已知用科学记数法表示的数，写出原来的数；
3．懂得用科学记数法表示数的好处；
活动一（情景步入）
我们知道：光的速度约为：300000000米/秒，地球表面积约
为:510000000000000平方米。

这些数非常大，写起来表较
麻烦，能否用一个比较简单的方法来表示这两个数吗？
活动二(合作探究）
1.把下列各数写成幂的形式:10 = ; 100= ; 1000= ;
10000= ; 100000= . 1000000=
归纳:由上述结果，你发现的规律是：100…0（在1的后面有n个0）可以
写成。

2.利用10的乘方可以表示一些大数：
567000000=5.67× = 5.67×10
即：5.67×108读作：。

[来源:学&科&网Z&X&X&K][来源:学。

科。

网]
- 83680000= × = ×；
即：读作：。

结合探究（1）（2）归纳：把一个大于10的数表示为a×10n的形式，其中a是整数位只有位的数，（即a< ）n是，这种记数的方法叫做科学记数法。

活动三（运用新知）
1.如果一个数是６位整数，用科学记数法表示它时,10的指数是；如果一个数是9位整数，用科学记数法表示它时，10的指数是；如果一个数是n位整数，用科学记数法表示它时，10的指数是 ; 用科学记数法表示数时，10的指数是5时，则原数是一个位整数；用科学记数法表示数时，10的指数是n时，则原数是一个位整数.。

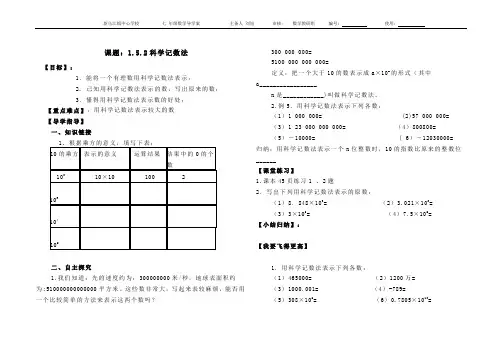
课题：1.5.2科学记数法【目标】：1．能将一个有理数用科学记数法表示；2. 已知用科学记数法表示的数，写出原来的数；3．懂得用科学记数法表示数的好处；【重点难点】：用科学记数法表示较大的数【导学指导】一、知识链接二、自主探究1.我们知道：光的速度约为：300000000米/秒，地球表面积约为:510000000000000平方米。

这些数非常大，写起来表较麻烦，能否用一个比较简单的方法来表示这两个数吗？300 000 000=5100 000 000 000=定义：把一个大于10的数表示成a×10n的形式（其中a_________________n是____________)叫做科学记数法。

2.例5．用科学记数法表示下列各数：（1）1 000 000= (2)57 000 000=（3）1 23 000 000 000= （4）800800=（5）－10000= ( 6）－12030000= 归纳：用科学记数法表示一个n位整数时，10的指数比原来的整数位______【课堂练习】1.课本45页练习1 、2题2．写出下列用科学记数法表示的原数：（1）8．848×103= （2）3.021×102=（3）3×106= （4）7.5×105=【小结归纳】：【我要飞得更高】1．用科学记数法表示下列各数：（1）465000= （2）1200万=（3）1000.001= （4）-789=（5）308×106= （6）0.7805×1010=【我的疑惑或收获】：课题：1.5.3近似数【教学目标】：1．了解近似数和有效数字的概念，能按要求取近似数和保留有效数字；2．体会近似数的意义及在生活中的应用；【教学重点】：能按要求取近似数和有效数字； 【教学难点】：有效数字概念的理解。

【自主探究】一、知识链接1．用科学记数法表示下列各数： （1）1250000000= ；（2）-130000= ；（3）-1025000= ；2．下列用科学记数法表示的数，把原数写在横线上：（1）=⨯-51003.2 ；（2）=⨯7108.5 ；二．自主探究1．（1）我们班有 名学生， 名男生， 名女生； （2）一天有 小时，一小时有 分，一分钟有 秒； （3）我的体重约为 千克，我的身高约为 厘米； （4）我国大约有 亿人口． 在上题中，第 题中的数字是准确的，第 题中的数字是与实际接近的。

《1.5.2 科学记数法》导学案一、学习目标1.通过身边数据进一步体会大数，培养学生的数感。

2.学会用科学记数法表示大于10的数3.会把用科学记数法表示的数还原。

二、探究学习学生阅读教材第44、45页完成下列问题1.10的n次幂在1后面有【】个0。

如：（1）102= （2）103= （3）104=反过来，把下列各数写成 10的幂的形式（1）100 = （2）1000 = （3）1 000 000=2.什么叫科学记数法？下列记数方式是科学记数法吗？说明理由（1）13×102（2）0.6×103（3）1.5×1043.用科学记数法表示一个数时，10的指数n与原数的整数位数有什么关系？如果一个用科学记数法表示的数是3.12 ×103，则原来的数【】,原数的整数部分有【】位数,这里n=【】，比原数的整数位数【】。

三、尝试练习1. 用科学记数法表示下列各数：神六飞船在太空中大约飞行 3 200 000千米.太阳的半径为 696 000 000千米;光的速度为 300 000 000 米/秒;我国人口已达1 300 000 000人;像下面那样，把一个数表示成a×10n的形式（其中1≤a＜10，n是整数），既简单明了，又便于阅读和进行计算，这种记数法，习惯上叫科学记数法(scientific notation) 。

在用科学记数法表示一个数的时候，怎样快速地确定出形式中的a和n呢?方法归纳：法一：小数点往左移动几位，则10的指数就是几法二：10的指数是原数整数位数减1，即若原数是m位整数，则10的指数为________ 2．下列用科学记数法记出的数，原来各是什么数？2×106= 6.03×105 = 5.002×104=四、课堂练习：练一练:1、用科学记数法表示下列各数。

①32 000 ②384 000 000③－810 000 ④9 410 000⑤510 600 ⑥10 000 000⑦32 100 000 ⑧－223 0002、用科学记数法记出下列各数：(1)地球离太阳约有一亿五千万千米；(2)地球上煤的储量估计为15万亿吨以上．辨一辨1、地球半径约为150 000 000 000米可用科学记数法表示为15×1010米 ( )2、2003年，我市实现国内生产总值218.4亿元,可用科学记数法表示为0.2184×1013元( )3、上半年，全国财政收入10954．99亿元，可用科学记数法表示为10.95499×1014元( )用一用1.一个正常人的平均心跳速率是每分70次，一年大约跳多少次？用科学记数法表示这个结果。

《科学记数法》导学案一、学习目标1、理解科学记数法的意义。

2、会用科学记数法表示绝对值较大的数。

二、学习重点1、掌握科学记数法的表示形式。

2、正确使用科学记数法表示数。

三、学习难点将一个绝对值较大的数用科学记数法表示。

四、知识回顾1、计数单位：个、十、百、千、万、十万、百万、千万、亿……2、整数的数位顺序表：五、新课导入在日常生活中，我们经常会遇到一些非常大的数，比如地球的半径约为 6400000 米，光的速度约为 300000000 米/秒。

这些数书写起来很不方便，读起来也很费劲。

那有没有一种更简便的方法来表示这些数呢？这就是我们今天要学习的科学记数法。

六、知识讲解1、科学记数法的定义把一个大于 10 的数表示成a×10ⁿ的形式（其中1≤｜a|＜10，n 是正整数），这种记数方法叫做科学记数法。

例如：567000000 可以表示为 567×10⁸2、用科学记数法表示数的方法（1）确定 a：a 是只有一位整数的数，即1≤｜a|＜10。

（2）确定 n：n 等于原数的整数位数减 1。

例 1：用科学记数法表示 123000000解：123000000 ＝ 123×10⁸例 2：用科学记数法表示 58000解：58000 ＝ 58×10⁴3、将科学记数法表示的数还原成原数原数＝a×10ⁿ 中 a 的小数点向右移动 n 位。

例 3：将 35×10⁵还原成原数解：35×10⁵＝ 350000七、课堂练习1、用科学记数法表示下列各数：（1）320000（2）57000000（3）123000000002、下列用科学记数法表示的数，原数各是什么？（1）25×10⁶（2）78×10⁵（3）301×10⁷八、课堂小结1、科学记数法的定义。

2、用科学记数法表示数的方法。

3、将科学记数法表示的数还原成原数的方法。

九、课后作业1、课本第____页第____题。

课题：第1.5.2 科学计数法学习目标:知识目标：利用10的乘方，进行科学记数，会用科学记数法表示大于10的数.能力目标：会解决与科学记数法有关的实际问题情感态度和价值观：正确使用科学记数法表示数，表现出一丝不苟的精神.教学重点与难点：教学重点：会用科学记数法表示大于10的数教学难点：正确使用科学记数法表示数学习过程一、自主探究1、创设情境，引入新课1）请同学们阅读如下材料：①能源:目前全球有2000000000人用不上电；②地球之肺:近10年来，全球消失的森林总面积达到94000000公顷；③生命之源 :全球有1100000000人未能用上安全饮用水。

这样的大数，读、写都不方便，怎么才能把这些句子读的快速又准确？2、自主学习1) 根据乘方的意义，填写下表：10的乘方中的_______=结果中________2)试着把下列各数写成10的乘方的形式：100=_______， 1000 000＝________， 1000 000 000＝________，1000 000 000 000＝________， 1 000……000=________n个03、合作交流能不能把材料中的数表示成整数数位只有一位的数乘以10的多少次幂的形式吗？2 000 000 000=__________=________94 000 000=__________=________1 100 000 000=__________=________请同学们再次尝试阅读1）中的材料。

1.自我尝试例1. 用科学记数法表示下列各数：1 000 000，57 000 000，-123 000 000 000组内交流：观察：等号左边的位数与右边10的指数有什么关系？归纳：用科学记数法表示一个n位整数，其中10的指数是_____.2.巩固提升用科学记数法表示下列小题中的量：①太阳的半径约为696 000 000米；②光的速度是300 000 000米/秒；3.拓展应用例2.中国森林面积约为1.2863×108公顷，写出用科学记数法表示的数的原数吗？练习：已知下列用科学记数法表示的数，写出原来的数．①6×104②2.01×105③-104总结方法:要将a×10n还原成整数就是把小数点向_____移动_____位，即a×10n原数的整数位数等于_______,如果a中的位数不够，用“0”补足，注意符号。

新人教版七年级数学上册第一章导学案1.5.2科学计数法学习目标：1、会用科学计数法表示较大的数2、掌握科学计数法的概念重点：1、能用科学计数法描述生活中的数据2、能够把一个数写成a×10n，其中：1≤|a|<10的数一、学习过程：1、计算：① 102=_____________② 103=10×10×10=_______③ 104=10×10×10×10=_________④ 105 =10×10×10×10×⑤ 106=10×10×10×10×10×10=______________________⑥ 10n中，1后面几个0？2、思考：（填上10的指数）①100=10____②1000=10_______③10000=10______④100000=10___⑤10000000000=10______3、阅读教材44—45页并完成以下填空：①______________________________叫做科学计数法②比如567000000=5.67×100000000=5.67×108，仿照上例解决以下问题a、57000000000=5.7×_____________________b、7400000=7.4×_____________________4、总结：小数点向右移动4位，就乘以_____________________，小数点向右移动n个位，则乘以_____________________二、例题解析1、用科学计数法表示下列各数10000000=104 1230000000000=1.23×________________ -42700000000000=-4.27×_____________________2、判断以下的变形是否正确，结果是否属于科学计数法形式325000=32.5×104 463000=0.463×106三、当堂训练1、2003年5月19日，国家邮政局特别发行“万众一心，抗击非典”邮票，收入全部捐赠给卫生部门，用以支持抗“非典”斗争．其邮票发行量为12 500 000枚，用科学记数法表示正确的是( )A．1.25×105枚B．1.25×106枚 C．1.25×107枚 D．1.05×108枚2、为了充分利用我国丰富的水力资源. 国家计划在四川省境内的长江上游修建一系列大型水力发电站，这些水力发电站的年发电总量相当于10座三峡电站．因此，四川省境内的这些水力发电站的年发电总量可达到847 000 000 000千瓦是，把它用科学记数法表示为( )A．8.47×1011千瓦时 B．847×109千瓦C．8.47×1010千瓦时 D．0.847×1012千瓦时3、今年6月5日是第33个世界环境日，其主题是“海洋存亡，匹夫有责”．目前全球海洋总面积约为36 105.9万平方公平，用科学记数法(保留三个有效数字)表示( )A．3.61×108平方公里 B．3.60×108平方公里C．361×108平方公里D．36 100万平方公里4、已知光的速度为300000000米/秒．太阳光到达地球的时间大约是500秒，试计算太阳与地球的距离大约是多少米5、实施西部人开发战略是党中央面向21世纪的重大决策，西部地区占我国国土面积的三分之二，我国的国土面积大约为960万平方米千米．用科学计数法表示我国西部地区的面积．四、课下训练1、地球上煤的储量估计为15万亿吨以上，用科学记数法可表示为( )A．1.5×1013 B. 1.5×1012C．1.5×1011 D．1.5×10102、从“第二届互联网大会”上获悉. 中国的互联网上网，用户数已超过7800万，居世界第二位，7800万用科学记数法表示为( )A．7.8×106 B. 7.8×107C．7.8× 108 D．0.78×1083、2003年10月15日．我国成功发射了第一艘载人航天飞船“神州五号”．成为中华人民共和国航天史上有一新的里程睥．已知赤道的周长为4×104千米，飞船绕地球行驶14圈所上的路程是多少千米？(用科学计数法表示)★4、地球每小时绕太阳转动约1.0×105千米．声音在空气中每小时约传播1.2×103千米. 试问，地球转动的速度与声音传播的速度哪个大？反思：比较两个科学记数法的大小，若n相同, 则a的值越大的数值越大, 另外当n 越大时, 数值越大．★5、一天有8.64×104秒，一年如果按365天计算，一年有多少秒?(用科学计数法表示)．★★五、拓展创新应用1、一种电子计算机每秒可做次108计算，用科学记数法表示它工作8分种可以计算( )A.8×108次 B.480×108次C.4.8×1010次D.4.8×1011次2、一只苍蝇腹内细菌多达2 800万个，用科学记数法表示这个数．3、如果一对鲑鱼—年能产200粒卵，这些卵全部成活并且雌雄各半，它们都进入生殖期，鲑鱼寿命只有一年，即产孵后成鱼全部死亡，那么13年后，这对鲑鱼能变成多少对?。

人教版七年级数学上册1.5.2《科学计数法》导学案【学习目标】1．会用科学记数法表示大于10的数；弄清科学记数法中10的指数n与这个数的整数位数的关系；2．知道如何用科学记数法表示的数的原数．3．感受科学记数法的作用，体会科学记数法表示大数的优越性及必要性．重点：正确运用科学记数法表示较大的数．难点：正确掌握10的幂指数特征．【学习过程】一、旧知回顾，问题诱思任务一、了解科学记数法的意义1．回顾有理数的乘方运算，算一算：10＝10＝10＝10＝_（1）(—10)表示（2）10n=10…..0（在1后面有个0）．2．借助10的乘方的特点记数：归纳：科学记数法的概念：一个大于的数可以表示成的形式，其中1≤a＜10，n是正整数，这种记数方法叫做科学记数法．试一试：用科学记数法表示下列各数：(1)1 000 000；(2) 57 000 000；(3)696 000；(4) -78 000；___任务三：会将用科学记数法的数还原成原数：下列用科学记数法表示的数，它的原数是什么？（1）3.8×10=；(2)5.007 ×107=；（3）5.9406×102=______________；（4）—7.0010×=______________．注意:1.科学记数法中的a的范围_____________；2.把科学记数法表示的数还原时，只要把a×10中a的小数点向右移动位即可．任务四：科学计数法的应用与拓展：请你把其中的数据用科学记数法表示出来：（1）人的大脑约有10,000,000,000个细胞：．（2）全世界人口约为61亿人：人．变式一：（1）2012年某省国内生产总值达到6030亿元：_________________亿元．（2）18547.9亿元=元．变式二：(3)50302=_________；(4)16.71×104=________；(5)0.0051×106=________．注意：（1）用科学记数法表示实际问题中的数量时，必须带上单位；（2）单位的统一．变式三：你能用科学记数法表示吗？（1）-56 0300 0000 0000=___________；(2)-50.01×106=_____________．注意：小于—10的数也可以用科学记数法表示，只是多一个负号，记作—a×10变式四：若a=6.3×106，则a的整数位数是（）A．5B．6C．7D．8三、围绕问题，反思总结本节课你有什么收获？有哪些注意点？⑴什么叫做科学记数法？．⑴灵活运用科学记数法，注意解题技巧，总结解题规律．⑴用科学记数法表示大数应注意以下几点：⑴１≤a＜10．⑴当大数是大于10的整数时，n为整数位减去1．。

）
A、 n 个 10 相乘所得的积 B、10 后面有 n+1 个 0 的整数
B、是一个 n+1 位的整数 D、是一个 n+2 位的整数
8、用科学计数法表示下列各数
（1）100000
（2） 378000 （3）－112000 （4）2945
（5）1346.30
5、用科学记数法表示一天，一年有多少秒
9、已知下列用科学记数法表示的数，写出原来的数。
§2.12 科学计数法
【教学目标】：
1、复习和巩固有理数乘方的概念，掌握有理数乘方的运算。 2、借助身边熟悉的事物进一步体会大数. 3、使学生了解科学记数法的意义，并会用科学记数法表示比较大的数
【重 点】：正确运用科学记数法表示较大的数。 【难 点】：正确掌握 10 的幂指数特征。 【学习过程】：
一、复习和预习
1≤a＜10， a 是正整数. 四、巩固练习
能力提升
1、“5·12 汶川大地震”发生后，中央电视台于 5 月 18 日承办了《爱的奉献》晚会，共募善
基础自测
1、我国研制的“曙光 3000 超级服务器”它的峰值计算速
度达到 403，200，000，000 次/秒，用科学记数法可
表示为
Hale Waihona Puke 次/秒.2、2000 年我国第五次人口普查资料表明，我国人口总
数为 12.9533 亿人，用科学记数法表示为：
3、2000 年某省国内生产总值达到 6030 亿元，用科学记数
法表示应记作（
）
A、60.3× 102 亿元
B、6.03 × 102
C、6.03 × 103 亿元
D、6.03 ×
10 4
款约 1 514 000 000 元，这个数字用科学记数法表示为__________元。

科学计数法导学案课题：1.5科学记数法2014级_____班_____组_____【学习目标】理解掌握科学记数法的意义，会用科学记数法表示绝对值大于10的数.【学习重点】：正确应用科学记数法表示绝对值大于10的数。

【学习难点】：正确掌握10n(n为正整数)的特点。

【导学指导】1：用15分钟左右的时间，阅读探究课本的内容，熟记基础知识，自主高效预习，提升自己的阅读理解能力；2完成教材助读设置的问题。

然后结合课本的基础知识和例题，完成预习自测题；3：将预习中不能解决的问题标出来，并写到“我的疑惑”处。

预习案：一：旧知回顾：回顾有理数的乘方运算，根据乘方运算得到：10×10×10×10=104 由乘法法则得到：10×10×10×10=10 000，所以104=10 000二：教材助读：1：根据你的理解什么是科学记数法？2：你能将光的传播速度300 000 000（单位：米/秒）用科学记数法表示吗？三：预习自测：认真自学课本，深入思考，通过下面几道题检验一下自己的自学成果。

1，用科学记数法表示下列各数：34=_________ —57 000=___________25 000 000 000 000=___________; —106 000 000=____________57 500 000 000=_______________.2：根据以下内容，把其中的数据用科学记数法表示出来。

(1)第五次人口普查时，中国人口约为1300000000人．(2)地球半径约为696000000米．(3)光的速度约为300000000米/秒(4)地球离太阳约有1亿五千万千米．(5)地球上煤的储量估计15万亿吨以上四．我的疑惑：通过预习你有什么收获？还有哪些疑惑，与同学们交流一下。

并把你在预习中未解决的问题和有疑惑的问题写下来。

探究案：一、学始于疑——我思考、我收获1、用科学记数法可以表示怎样的数?任何数都能用科学记数法表示吗？2、用科学记数法表示的数中n是如何确定的？学习建议：请同学们用2分钟时间认真思考这些问题，并结合预习中自己的疑惑开始下面的探究学习。