概率统计和随机过程课件11.2随机过程的数字特征
- 格式:pdf
- 大小:120.59 KB
- 文档页数:31
![随机过程[2]](https://uimg.taocdn.com/9e7d0841c850ad02de8041e2.webp)


2.1. 随机过程的描述1. 随机过程的概念随机过程:考察各测量样本固定时刻0t t =在0t 时刻的值)(01t x ,)(02t x ,……,)(0t x n 构成随机变量,具有自身的概率特性,记为)(0t X 。
在数学上把所有已经得到的和未得到的而可能发生的样本总体)}({0t x i (t=1,2,3,……)称为随机过程,记为)(t X 。
随机过程具有双向无穷特征,即在时间轴上无穷,又在样本数上无穷。
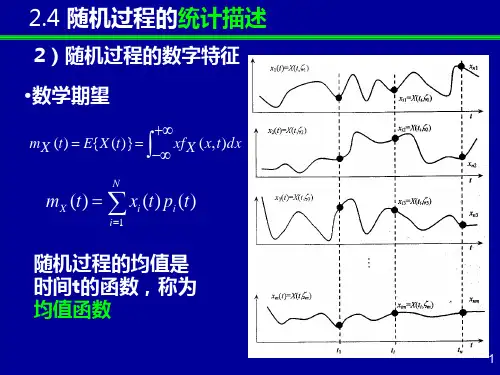
2. 随机过程的统计规律(1). 一维概率分布特征设一随机变量)(t X 在某一时刻i t 的随机变量)(i t X 的取值小于等于给定值x ()(t X x ∈),这一事件发生的概率定义为:])([Pr );(1x t X ob t x F i i ≤=,)(t X x ∈)(t X 的一维概率密度函数);(1i t x f 定义为);(1i t x F 对x 的一阶偏导数,即:xt x F t x f i i ∂∂=);();(11 (2). 多维概率分布特征 二维概率分布特征随机过程)(t X 在i t 时刻的随机变量i i x t X ≤)(;而且在j t 时刻的随机变量j j x t X ≤)(,这两件事同时发生的概率定义为二维概率分布特征:])(,)([Pr ),;,(2j j i i j i j i x t X x t X ob t t x x F ≤≤=二维概率密度函数为对j i x x ,的二阶偏导数,即:j i j i j i j i j i x x t t x x F t t x x f ∂∂∂=),;,(),;,(222三维、四维,……直至n 维可以以此类推实际应用中,要确定随机过程的各维概率分布函数及密度函数非常困难3. 随机过程的统计特征量(1). 均值)(t m x也就是随机过程的数学期望吗,度量过程随机变动的平均值dx t x xf t X E t m i x ⎰∞∞-==);()]([)(1 由于)(t X 在不同时刻的一维概率密度函数);(1t x f 是对时间t 的函数,故均值)(t m x 亦随时间而变。






什么是随机过程(一)引言概述:随机过程是概率论和数学统计学中的重要概念,用于描述随机事件在时间和空间上的演化规律。
它在实际问题建模和分析中具有广泛的应用,涵盖了大量的领域,如通信系统、金融市场、生物学等。
本文将介绍随机过程的基本概念和特征,并探讨其在实际中的应用。
正文:1. 随机过程的定义1.1 随机过程的基本概念1.2 随机变量与随机过程的关系1.3 不同类型的随机过程(如离散随机过程、连续随机过程等)2. 随机过程的特征2.1 随机过程的时间域特征2.2 随机过程的统计特征2.3 随机过程的独立性和相关性2.4 随机过程的平稳性2.5 随机过程的马尔可夫性质3. 随机过程的应用3.1 通信系统中的随机过程3.2 金融市场中的随机过程3.3 生物学中的随机过程3.4 物理学中的随机过程3.5 工程控制中的随机过程4. 随机过程的建模和分析方法4.1 马尔可夫链模型4.2 随机演化方程模型4.3 随机微分方程模型4.4 随机过程的仿真方法4.5 随机过程的参数估计方法5. 随机过程的未来发展5.1 随机过程在人工智能中的应用5.2 随机过程在时空数据分析中的应用5.3 随机过程在大数据分析中的应用5.4 新兴领域中的随机过程研究5.5 随机过程理论与实际应用的结合总结:本文介绍了随机过程的定义、特征和应用,并讨论了随机过程的建模和分析方法。
随机过程作为概率论和数学统计学的重要分支,具有广泛的应用前景。
随着人工智能和大数据分析的发展,随机过程在各个领域中的应用将进一步扩展。
值得期待的是,未来随机过程理论和实际应用的结合将推动该领域的进一步发展。

随机过程的数字特征
<概率统计习题解>, 15元一本地点: 主南311
第三节随机过程的数字特征
随机变量数字特征复习:
Y X ,为随机变量, 联合概率密度),,(y x f 边沿概率密度)
(),(y f x f Y X 数学期望(均值)
⎰⎰⎰+∞∞-+∞
∞-+∞∞-==dxdy
y x xf dx x xf EX X ),()(=)],([Y X g E ⎰⎰+∞∞-+∞
∞-dxdy
y x f y x g ),(),(
二阶原点矩
⎰⎰⎰+∞∞-+∞∞-+∞∞-==dxdy
y x f x dx x f x EX X ),()(2
22方差dx
x f EX x EX X E DX X )()()(22⎰+∞
∞--=-=2
2)(EX EX -=二阶原点混合矩⎰⎰+∞∞-+∞
∞-=dxdy
y x xyf XY E ),()(
随机过程的数字特征
是参数集,T ),(+∞-∞⊂T 随机变量族}),({T t t X ∈是一个随机过程,(11.1)
(1)过程在的状态的数学期望t )(t X 对于任意给定,t T ∈的状态)(t X ,具有一维概率密度)
;(11t x f 在t 时刻dx t x xf t X E t X );()]([)(1⎰+∞
∞-==μ
对于一切,t T ∈称为随机过程)(t X 的均值函数,简称均值;
是的函数,
t ()X t μ(2)过程在
的状态的二阶原点矩t )(t X dx t x f x t X E t X );()]([)(1222
⎰+∞∞-==ψ(11.2)
称为随机过程的均方值函数,简称均方值;
)(t X
(3)二阶中心矩(方差)
2
2)]()([)]([)(t EX t X E t X D t X
-==σ2
)]()([t t X E X μ-=)()]([2
2t t X E X μ-=(11.3)
称为随机过程的方差函数,简称方差,)(t X 均方差;
)(t X σ
任选, 状态是两个随机变量,T t t ∈21,)(),(21t X t X 具有二维概率密度)
,;,(21212t t x x f (4)随机过程的自相关函数,简称相关函数,
)(t X )]
()([),(2121t X t X E t t R X ⋅=212121221),;,(dx dx t t x x f x x ⎰⎰+∞∞-+∞
∞-=(11.4)
1212(,)R t t t t 自相关函数关于和对称。
(5)随机过程的自协方差函数,)(t X 121122(,)
{[()()][()()]}X C t t E X t EX t X t EX t =-⋅-)]}
()([)]()({[2211t t X t t X E X X μμ-⋅-=(11.5)
简称协方差函数,1212(,)X C t t t t 协方差函数关于和对称。
均值、均方值、方差和均方差是刻划随机过程在各个状态的统计特性的,而自相关函数和自协方差函数是刻划随机过程的任何两个不同状态的统计特性的.这五个数字特征之间,具有如下关系.
22
()[()][()()](,)
X
X t E X t E X t X t R t t ψ==⋅=121122(,){[()()][()()]}
X C t t E X t EX t X t EX t =-⋅-)]}()([)]()({[2211t t X t t X E X X μμ-⋅-=)]
(),(cov[21t X t X =)
()()]()([2121t EX t EX t X t X E ⋅-⋅=)
()(),(2121t t t t R X X X μμ⋅-=
2
2)]
()([)]([)(t EX t X E t X D t X
-==σ2
)]
()([t t X E X μ-=2((,),)()
X
X X R t t C t t t μ==-)()]([22
t t X E X
μ-=)
()(22t t X
X
μ-ψ=通过以下例子,就可以看出随机过程数字特征的实际意义.
例1
设随机相位正弦波)cos()(Θ+=t a t X ω+∞
<<∞-t 式中是常数,
ω,a Θ是在区间)
2,0(π上服从均匀分布的随机变量.
求:
的均值函数、方差函数、自相关函数和自协方差函数. )(t X 解:依题意的概率密度为
Θ
例2: 设随机过程Yt
X t Z +=)(+∞
<<∞-t 式中服从, 服从,
X )
,(21
σa N Y ),(22
σb N 且与的相关系数,
X Y ρρ=XY 求:
的自相关函数.)(t Z 121222
1212(,)[()()]()()()()
=++=+++R t t E X Yt X Yt E X t t E Y t t E XY 解:
设随机过程的数学期望为协方差函数而是一个函数。
试求随机过程 的数学期望和协方差函数。
12{(),-}(),(,),()()()()
x X X t t m t C t t t Y t X t t ϕϕ∞<<+∞=+例4[()][()()]()
X E Y t E X t t m t ϕϕ=+=+=-==1212121212cov(,)[()()][()][()]
cov (,)(,)
X X t t E Y t Y t E Y t E Y t t t C t t 解
对于两个随机过程和,}),({1T t t X ∈}),({2T t t Y ∈和)(1t X 过程在的状态.
)(t Y 2t )(2t Y 和的二阶原点混合矩
)
(1t X )(2t Y )]
()([),(2121t Y t X E t t R XY =(11.7)
称为随机过程和的互相关函数;
)(t X )(t Y 任选1122,,
t T t T ∈∈)(t X 1t 过程
在
的状态
两个随机过程的联合分布和数字特征
和的二阶中心混合矩
)(1t X )(2t Y )]}
()()][()({[),(221121t t Y t t X E t t C Y X XY μμ--=(11.8)
称为随机过程和的互协方差函数;
)(t X )(t Y 并且有
12(,)X Y C t t =1212(,)()()
XY X Y R t t t t μμ=-1212[()()][()][()]
XY X Y E X t Y t E X t E Y t -问题:互相关函数,互协方差函数是否关于t 1, t 2对称?
定义: 如果对任意,都有
2211,T t T t ∈∈0),(21=t t C XY 亦即
)]
([)]([)]()([2121t Y E t X E t Y t X E ⋅=则称随机过程和是不相关的.)(t X )(t Y 显然,相互独立的两个随机过程必不相关.例5: 设某接收机收到周期信号电压)(t S 和噪声电压
)
(t N [()]0 E N t =,
, 且设
的均值,自相关函数与输入电压
)()()(t N t S t V +=的数字特征的关系., 互不相关.()N t 且)(t S 与()(()())()
V S u t E S t N t u t =+=121122(,)[(()())(()())] =++V R t t E S t N t S t N t 解
试导出输出电压
12121212[()()][()()]
[()()][()()]
=+++E S t S t E N t S t E S t N t E N t N t
1212121212()()[()()][()()]0.(,)(,)(,)
V N S S t N t E N t S t E S t N t R t t R t t R t t ===+由于与互不相关
所以
作业
•习题5,7,8,9,11
31。