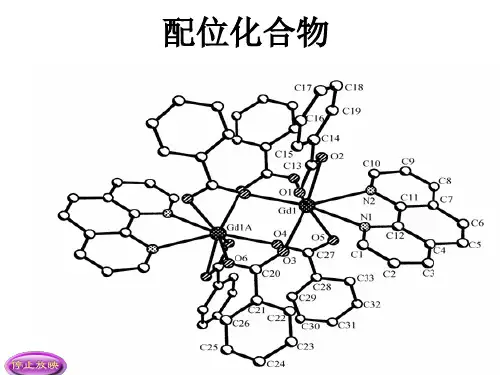
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2g1eg1 →1T1g+1T2g+3T1g+3T2g eg2 → 1A1g+ 1Eg + 3A2g 两种方法应该得到相同的结果。
三 d-d光谱
(1) d-d光谱的特征
ⅰ强度
电子从一个能级跃迁到另一个能级必须遵守一定的规律, 这种规律称为 光谱选律。光谱选律有两条:
① 自旋选律, 也称多重性选择 多重性(2S+1)相同谱项间的跃迁是允许的跃迁 , 多重性不
+2
+1
0 -1 -2
1 1 2 1 1 3 1 1 2 1 1
根据这 个表, 我们 可以从中找 出相应的光 谱项。例如, 取出一组: 再取出一组
MLMs
+2
+1
0
0
-1 -2
1 1 1 1 1
ML=2, 1, 0 Ms=0
即
L=2, S=0 1D (简并度5) 包括5个微态 还余1个微态 M Ms 0
L
还余10个微态 MLMs
+1
M +1 0 -1 ML s +1 0 -1
1 1 1 1 2 1 1 1 1
+1
ML= 1, 0 Ms= 1, 0
即
0 -1
0 -1
1 1 1 1 1 1 1 1 1
L=1, S=1 3P (简并度9) 包括9个微态
1 0 ML=0, Ms= 0 即 L=0, S=0 1S (简并度1)
照这样可对上述微态组合分别写出光谱项, 如 L=2, S=0, 1D 简并度5, 单重态, 无未成对电子 简并度除能从行列式看出以外, 还可由下列关系式直接计算: 简并度=(2L+1)(2S+1)
例:d 2组态:
ml = +2
+1
0
–1
–2
……………………. ms=1/2,45种可能的排列(微状态)
380 780
435
紫 紫 蓝 480 红 红 绿蓝 490 650 蓝绿 橙 黄 绿 500 598 黄 绿
580 560
6.1 配体内部的电子光谱
配位体如水和有机分子等在紫外区经常出现吸收谱带。形成配合物后, 这 些谱带仍保留在配合物光谱中, 但从原来的位置稍微有一点移动。
配位体内部的光谱包括以下三种类型: ① n→* 处于非键轨道的孤对电子到最低未占据的空轨道 ζ*反键轨道的跃迁。水、醇、胺、卤化物等配体常发生这类跃 迁。 ② n→* 处于非键轨道的孤对电子到最低未占据空轨道* 反键分子轨道的跃迁, 常出现在含羰基的醛和酮类分子中。 ③ →* 处于最高占据轨道分子轨道的电子向最低未占 据的空轨道*反键分子轨道跃迁, 这类跃迁经常出现在含双键、 叁键的有机分子中。
按照Hund 规则和Pauli原理
1.对于给定组态(L相同),自旋多重度越大,即自 旋平行的电子越多,能量越低。 S值越大,能量越低。
2.对于给定多重度(S相同),L大则电子间作用力小; L小, 电子间作用力大,能量高。例: 3F的能量低于3P。 L越大,能量越低。
2 基谱项
同一电子组态中能量最低的谱项称为基谱项, 基谱项可根 据洪特规则、保利不相容原理和能量最低原理来确定:
第六章 配合物的电子光谱
配合物的电子光谱属于分子光谱, 它是分子中电子在不同能级的分子轨 道间跃迁而产生的光谱。
根据电子跃迁的机理, 可将过渡金属配合物的电子光谱分为 三种:
d轨道能级之间的跃迁光谱, 即配位场光谱; 配体内部的电子转移光谱。 电子光谱有两个显著的特点: ①为带状光谱。这是因为电子跃迁时伴随有不同振动精细 结构能级间的跃迁之故。
一 自由离子光谱项
1 自由离子光谱项的推算
求某一电子组态的能级, 就是推导其光谱项, 实质上就是推 算该电子组态的不同L和S的组合。 以一个np2组态为例:
mL +1 0 -1 ML=ΣmL Ms=Σms
2 0 -2 1 0 -1 1 0 0 0 0 1 1 1 -1 -1 (1) (2) (3) (4) (5) (6) (7) (8)
下面用弱场方案处理d2电子组态的能级分裂情况。
D2 组态的电子相互作 用下分裂为五个能级: 1S >1G>3P>1D>3F, 且这些 光谱项在八面体配位场中 变为:
1S→1A 1g 1G→1A , 1T , 1E , 1T 1g 1g 1g 2g 3P→3T 1g 1D→1E , 1T g 2g 3F→3A , 3T , 3T 1g 2g 1g
p2组态有15种排布方式 mL +1 0 -1 ML=ΣmL Ms=Σms
-1 1 0 -1 1 0 -1 -1 (9) 0 (10) 0 (11) 0 (12) 0 (13) 0 (14) 0 (15)
把这15种可能的排布方式重新整理, 按每组的ML, Ms所包含 的微态数可以列成下面左上角的表。 MLMs +1 0 -1
配位体至金属离子或金属离子至配位体之间的电荷迁移光谱;
②在可见光区有吸收, 但强度不大。但在紫外区, 常有强度 很大的配位体内部吸收带。
过渡金属配合物电子运动所吸收的辐射能量一般处于可见区 或紫外区, 所以这种电子光谱通常也称为可见光谱及紫外光谱。 当吸收的辐射落在可见区时, 物质就显示出颜色。物质所 显示的颜色是它吸收最少的 那一部分可见光的颜色, 或 者说是它的吸收色的补色。 表10和下图给列出可见 光的吸收与物质颜色之间的 对应关系。
L=1, ML= 1, 0, L=0, ML= 0,
S=0
S=1 S=0
MS= 0
MS= 1, 0 MS = 0
用这种方法可以推算出不同d电子组态的光谱项(表11), 11
由表可见, d10-n与dn具有相同的谱项, 可通过“空穴规则” 来理解:在多于半满的壳层中, 根据静电观点, ―空穴”可理解成 正电子, 正电子也象电子那样会产生相互排斥作用。 如:d4, 四个电子占据五条轨道, d6, 四个空穴占据五条轨道, 产生的静电排斥作用相同。
ML= 0 MS =0
(2S+1)(2L+1)=1
能量相同的微状态归为一组,得到自由离子的5个光谱项:
L=4, ML= 4, 3, 2, 1 0,
L=3, ML= 3, 2, 1 0,
S=0
S=1
MS= 0
MS= 1, 0
1G
3F 1D 3P 1S
L=2, ML= 2, 1 0,
二 自由离子谱项在配位物中的分裂
如果一个dn电子组态的离子处于一个配位场之中, 这时将 存在两种相互作用: ●电子间的相互排斥; 二者大体上处于同一个数量级。 ●配体的静电场影响。
可用两种方式来估算这两种作用的综合影响:
*先考虑电子间的互相排斥作用, 换句话说先确定电子组态
的光谱项, 然后再研究配位场对每个谱项的影响, 这种方法称为 “弱场方案”。关于光谱项在配位物中的分裂情况见表13。
ML=4, 3, 2, 1, 0
MS =0
(2S+1)(2L+1)=9
ML= 3, 2, 1, 0 MS = 1, 0 (2S+1)(2L+1)=21
ML=2, 1, 0 MS =0 (2S+1)(2L+1)=5
ML=1, 0 MS = 1, 0 (2S+1)(2L+1)=9
由于角量子数l为偶数的轨道具有g对称性, 而角量子数为奇数的轨道具 有u对称性, 故从对称性的角度来说, △l=1, 3的轨道之间的跃迁是允许的, 而 △l=0, 2, 4是禁阻的。
上述两条光谱选律, 以自旋选律对光谱的强度影响最大, 其
次是轨道选律。
如果严格按照这两条选律, 将看不到过渡金属d-d跃迁, 当 然也就看不到过渡金属离子的颜色, 因为d-d跃迁是轨道选律 所禁阻的。 但事实却相反, 过渡金属离子有丰富多彩的颜色, 这是因为 上述禁阻往往由于某种原因而使禁阻被部分解除之故。 这种禁阻的部分解除称为“松动”。 例如, 在多电子体系中, 由于自旋-轨道偶合而使自旋禁阻 得到部分开放。 或自由离子的环境中缺乏对称中心, d轨道和p轨道的部分 混合产生d p跃迁,即产生部分允许跃迁。 又如, 配合物中, 由于某些振动使配合物的对称中心遭到了 破坏, d轨道和p轨道的部分混合使△L不严格等于0等都可使轨道 选律的禁阻状态遭部分解除。 然而, 虽然上述禁阻被部分解除, 但毕竟d-d跃迁是属于对 称性选律所禁阻的, 所以d-d跃迁光谱的强度都不大。
*第二种方法是先考虑配位场的影响, 然后再研究电子间的排
斥作用, 这种方法称为“强场方案”。 例如, d2组态的离子在八面体 强场作用下有三种可能的组态:
第二激发态(eg2) 第一激发态(t2g1eg1)
d2
基态(t2g2)
这三种组态中的电子间产生 相互作用而引起分裂(如左图):
t2g2 → 1A1g+ 1Eg + 1T2g + 3T1g
基谱项: ① 具有最高的自旋多重态, 即S最大的谱项; ② 当S相同时, L最大的谱项。 根据这种原则, 我们直接可以写出基谱项, 其办法是 a 尽可能在每条轨道上都安置一个电子, 以确保S最大; b 尽可能将电子安排在角量子数最大的那些轨道, 以确保L最大 c 计算ML和MS, 写出谱项符号。
如 d3 l= 2 1 0 –1 -2 ML=2+1+0=3 L=3 谱项字母为 F MS=3×1/2=3/2 2S+1=4
②在光谱项符号的右下角标记上J值, 就构成了光谱项的符号: 2S+1L J 如:
3F
4P
3F 3F 3F 4 3 2 4P 4 4 5/2 P3/2 P1/2
对于同一光谱项包括的不同光谱支项的能级高低, 根据洪 特规则确定:
●当组态的电子数少于壳层半充满时以J值小的能级低; ●多于半满时, 以J值大时的能级为低; ●半满时, 由于L=0, S必定≥L, J值有2L+1=1个。 如, 对于d2, 壳层电子数少于半充满, 故 3F > 3F > 3F 4 3 2