电路-第9章 网络图论基础

图论基本知识对于网络的研究，最早是从数学家开始的，其基本的理论就是图论，它也是目前组合数学领域最活跃的分支。

我们在复杂网络的研究中将要遇到的各种类型的网络，无向的、有向的、加权的……这些都可以用图论的语言和符号精确简洁地描述。

图论不仅为物理学家提供了描述网络的语言和研究的平台，而且其结论和技巧已经被广泛地移植到复杂网络的研究中。

图论，尤其是随机图论已经与统计物理并驾齐驱地成为研究复杂网络的两大解析方法之一。

考虑到物理学家对于图论这一领域比较陌生，我在此专辟一章介绍图论的基本知识，同时将在后面的章节中不加说明地使用本章定义过的符号。

进一步研究所需要的更深入的图论知识，请参考相关文献[1-5]。

本章只给出非平凡的定理的证明，过于简单直观的定理的证明将留给读者。

个别定理涉及到非常深入的数学知识和繁复的证明，我们将列出相关参考文献并略去证明过程。

对于图论知识比较熟悉的读者可以直接跳过此章，不影响整体阅读。

图的基本概念图G 是指两个集合(V ，E)，其中集合E 是集合V×V 的一个子集。

集合V 称为图的顶点集，往往被用来代表实际系统中的个体，集合E 被称为图的边集，多用于表示实际系统中个体之间的关系或相互作用。

若{,}x y E ，就称图G 中有一条从x 到y 的弧（有向边），记为x→y ，其中顶点x 叫做弧的起点，顶点y 叫做弧的终点。

根据定义，从任意顶点x 到y 至多只有一条弧，这是因为如果两个顶点有多种需要区分的关系或相互作用，我们总是乐意在多个图中分别表示，从而不至于因为这种复杂的关系而给解析分析带来困难。

如果再假设图G 中不含自己到自己的弧，我们就称图G 为简单图，或者更精确地叫做有向简单图。

以后如果没有特殊的说明，所有出现的图都是简单图。

记G 中顶点数为()||G V ν=，边数为()||G E ε=，分别叫做图G 的阶和规模，显然有()()(()1)G G G ενν≤-。

图2.1a 给出了一个计算机分级网络的示意图，及其表示为顶点集和边集的形式。

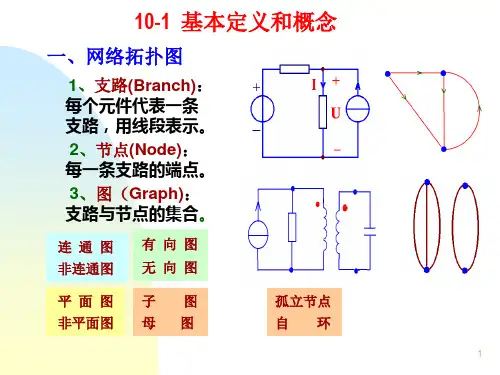
第九章网络图论基础9．2．1 网络图论的基本概念(1)图：由“点(节点)”和“线(支路)”组成的图形称为图，通常用符号G 来表示。

(2)子图：图的一部分(允许孤立的节点，不允许孤立的支路)。

(3)有向图：若图G的每条支路都标有一个方向，则称为有向图，否则称为无向图。

(4)连通图：若图中的任意两个节点之间均至少存在一条由支路构成的路径，则称为连通图，否则称为非连通图，孤立的节点也是连通图。

(5)数、树枝、连枝：不包含回路，但包含图的所有节点的连通的子图为树；组成树的支路为树枝；其余支路为连枝。

(6)回路：从图中某一节点出发，经过若干支路和节点(均只许经过一次)又回到出发节点所形成的闭合路径称为回路。

(7)基本回路：只含一个连枝的回路，也称单连枝回路。

(8)割集：割集是一组支路的集合，如果把这些支路全部移走(保留支路的两个端点)，则此图变成两个分离的部分，而少移去任一条支路，图仍是连通的。

(9)基本割集：只含一个树枝的割集，也称单树枝割集。

9．2．2 图的矩阵表示图的支路与节点、支路与回路、支路与割集的关联性质均可以用相应的矩阵来描述。

一、关联矩阵A关联矩阵A又称为节点支路关联矩阵，它反映的是节点与支路的关联情况。

设一有向图的节点数为n，支路数为b，则节点与支路的关联情况可以用一个n×b的矩阵来表示，记为Aa ，称为图的增广关联矩阵，Aa的每一行对应一个节点，每一列对应一个支路，其第i行第j列的元素aij定义为：由于Aa 的行不是彼此独立的，即Aa中的任一行都能从其他(n-1)行导出，因此，若由矩阵Aa中任意划出一行，剩下的(n-1)×b阶矩阵称为降阶关联矩阵，用A表示，又称为关联矩阵。

被划去的一行所对应的节点可当作参考节点。

二、回路矩阵B对于任一个具有n个节点，b条支路、c个回路的有向图，回路与支路的关联情况可以用一个(c×b)阶矩阵来描述，记为Ba ，Ba的每一行对应一个回路，每一列对应一个支路，其第i行第j列的元素bij定义为：若从矩阵Ba中取出独立回路所组成的(b-n+1)×b阶矩阵称为独立回路矩阵，简称回路矩阵。

网络拓扑知识：网络拓扑的图论基础网络拓扑图论基础网络拓扑，是指网络中各个节点（如服务器、路由器、交换机等）之间的连接关系和组成形式。

在网络建设和维护中，网络拓扑是一个重要的考虑因素。

图论是研究图形的学科，网络拓扑中的图像所表达的特征和特点也与图论有着密切的联系。

图是一种由节点和边构成的数学模型，常用于描述复杂的关系。

在图中，节点表示图中的个体，如人、物、场所等，在网络拓扑中，节点可以表示计算机、路由器、交换机等网络设备。

边表示这些个体之间的关系，如人与人之间的亲属关系、产品与产品之间的运输关系等，在网络拓扑中，边可以表示网络设备之间的连接方式和互联方式。

在图中，节点也可称为顶点，边也可称为线。

所以，一个图就是一个由顶点和边组成的集合，常用G（V，E）表示。

其中，G表示图，V表示顶点（vertex），E表示边（edge）。

图形常用非正式的语言来描述，如用不同的颜色、粗细、箭头、名称等来表示不同的节点和边。

以下是一个简单的例子：图中用圆形表示节点，用线连接两个节点表示这两个节点之间存在着一定的关系。

这张图就是一个无向图，即边没有方向性，任意两个节点之间都是相互连通的。

无向图中的节点可以分为度数为奇数和偶数的两种，满足每个节点的度数都是偶数的图称为欧拉图，任何欧拉图都可以通过从某个节点出发，沿着边，依次经过每个节点，回到出发节点形成闭合回路。

如果存在两个度数为奇数的节点，就是半欧拉图（或叫半欧拉回路），半欧拉图中可以从一个度数为奇数的节点出发，经过所有边恰好一次，到达另一个度数为奇数的节点。

若没有度数为奇数的节点，则没有欧拉通路或半欧拉通路的连通无向图为欧拉图。

有向图的边是带有方向性的，顶点之间的方向性是不同的，所以在有向图中，节点之间的关系是单向的。

因为有向图中边的方向性，定义节点的入度指向该节点的边的数量，而出度指从该节点出发的边的数量。

一个图中所有节点的出入度之和相等，则称其为欧拉图；如果每个节点的出度等于入度，则称为正则图；只有一个节点入度与出度之差为1，所有其他节点入度与出度相等，则该图为半欧拉图。