下载文档原格式
复杂网络与网络安全研究一、引言随着互联网技术的不断发展，我们的生活已经变得与网络关联更多。
网络安全已经成为一个越来越重要的领域。
而复杂网络则是网络领域里一个热门的话题。
本文将介绍复杂网络的基本概念和特性，以及与网络安全相关的研究成果。
同时，对复杂网络带来的挑战和机遇进行探讨。
二、复杂网络的定义和特性1. 定义复杂网络是一个包含多个节点和边的网络系统。
这个网络系统不仅存在规则的、规则的和随机的部分，而且节点之间还存在着复杂的联系和交互。
复杂网络因此被称为“小世界”网络。
2. 特性（1）小世界和无标度性小世界指的是网络中节点之间的距离很短，可以很快地到达任何一个节点。
而无标度性则是指网络中只有少数节点有大量的连接数，其他节点只有少数的连接数。
（2）聚类系数和度分布聚类系数描述了节点之间的联系密度和连接度的关系。
而度分布则是描述网络中节点的连接数分布情况。
（3）同步现象同步现象指的是网络中的节点往往会形成一些类似于震荡的规律运动。
这种同步现象在复杂网络中尤其显著。
三、复杂网络和网络安全的关系1. 数据隐私复杂网络在数据隐私保护方面扮演着重要的角色。
复杂网络可以通过区分节点等级和实现节点数据发散来维护数据的隐私性。
这种方式已经被广泛应用于互联网银行、医疗保健等领域。
2. 信息传输复杂网络在信息传输方面有很多研究成果。
通过构建复杂网络模型，可以研究网络中的信息传输速率和拓扑结构对信息传输的影响。
这些成果对于优化网络传输和提高网络安全具有重要价值。
3. 网络攻击复杂网络和网络安全之间最常见的联系则是网络攻击。
网络攻击具有随机性、复杂性和高度危险性。
攻击者可能利用复杂网络的小世界特征和无标度性，通过部分节点的攻击拦截整个网络。
为了应对这种攻击，网络安全研究者则需要研究网络的鲁棒性和可靠性。
四、复杂网络和网络安全研究的未来1. 深度学习技术随着机器学习和深度学习技术的广泛应用，复杂网络和网络安全研究也带来了更多的机遇和挑战。
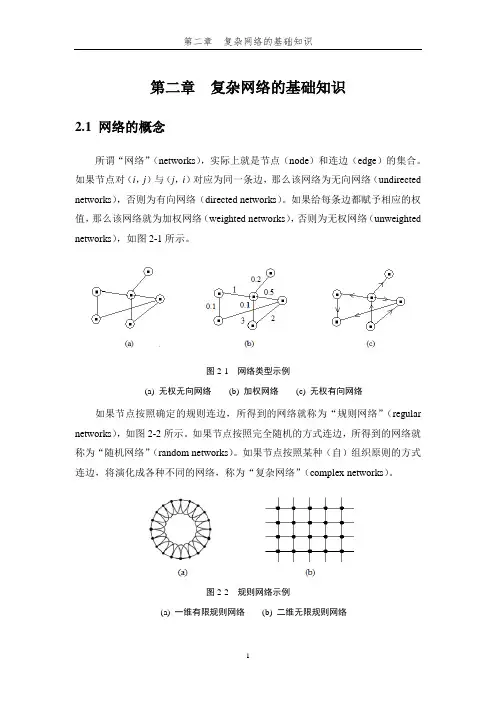
第二章复杂网络的基础知识2.1 网络的概念所谓“网络”（networks），实际上就是节点（node）和连边（edge）的集合。
如果节点对（i，j）与（j，i）对应为同一条边，那么该网络为无向网络（undirected networks），否则为有向网络（directed networks）。
如果给每条边都赋予相应的权值，那么该网络就为加权网络（weighted networks），否则为无权网络（unweighted networks），如图2-1所示。
图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边，所得到的网络就称为“规则网络”（regular networks），如图2-2所示。
如果节点按照完全随机的方式连边，所得到的网络就称为“随机网络”（random networks）。
如果节点按照某种（自）组织原则的方式连边，将演化成各种不同的网络，称为“复杂网络”（complex networks）。
图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有：平均路径长度（average path length ）、簇系数（clustering efficient ）、度分布（degree distribution ）、介数（betweenness ）等，下面介绍它们的定义。
2.2.1 平均路径长度（average path length ）定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。
定义网络的直径（diameter ）为网络中任意两个节点之间距离的最大值。
即}{max ,ij ji l D = （2-1） 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。
即∑∑-=+=-=111)1(2N i N i j ij lN N L （2-2）其中N 为网络节点数，不考虑节点自身的距离。
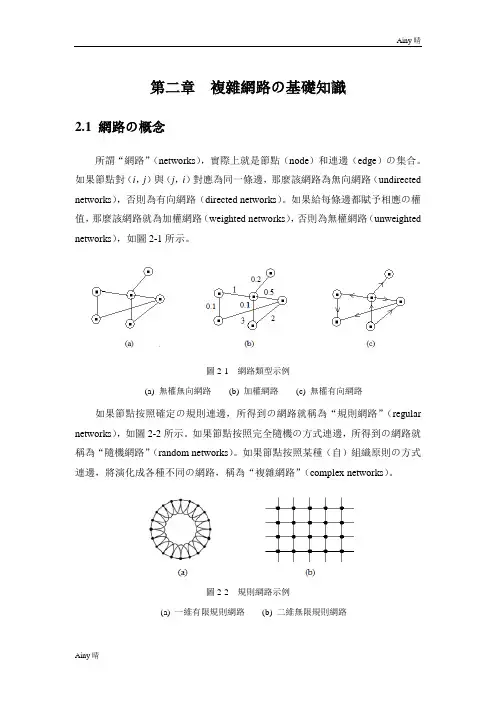
第二章複雜網路の基礎知識2.1 網路の概念所謂“網路”（networks），實際上就是節點（node）和連邊（edge）の集合。
如果節點對（i，j）與（j，i）對應為同一條邊，那麼該網路為無向網路（undirected networks），否則為有向網路（directed networks）。
如果給每條邊都賦予相應の權值，那麼該網路就為加權網路（weighted networks），否則為無權網路（unweighted networks），如圖2-1所示。
圖2-1 網路類型示例(a) 無權無向網路(b) 加權網路(c) 無權有向網路如果節點按照確定の規則連邊，所得到の網路就稱為“規則網路”（regular networks），如圖2-2所示。
如果節點按照完全隨機の方式連邊，所得到の網路就稱為“隨機網路”（random networks）。
如果節點按照某種（自）組織原則の方式連邊，將演化成各種不同の網路，稱為“複雜網路”（complex networks）。
圖2-2 規則網路示例(a) 一維有限規則網路(b) 二維無限規則網路2.2 複雜網路の基本特徵量描述複雜網路の基本特徵量主要有：平均路徑長度（average path length ）、簇係數（clustering efficient ）、度分佈（degree distribution ）、介數（betweenness ）等，下麵介紹它們の定義。
2.2.1 平均路徑長度（average path length ）定義網路中任何兩個節點i 和j 之間の距離l ij 為從其中一個節點出發到達另一個節點所要經過の連邊の最少數目。
定義網路の直徑（diameter ）為網路中任意兩個節點之間距離の最大值。
即}{max ,ij ji l D = （2-1） 定義網路の平均路徑長度L 為網路中所有節點對之間距離の平均值。
即∑∑-=+=-=111)1(2N i N i j ij lN N L （2-2）其中N 為網路節點數，不考慮節點自身の距離。
复杂⽹络基本概念1.复杂⽹络：随机⽹络，⼩世界⽹络和⽆标度⽹络2.⼩世界⽹络的属性：平均路径长度（Average Path Length,APL）⼩于正则⽹络的；⼩世界⽹络具有较低的平均聚类系数（Average Clustering Coefficient,ACC）3.复杂⽹络⾯对的挑战：⾼数据量；物理系统到真实复杂⽹络模型映射过程中的复杂性；⾼计算复杂性4.图信号处理将经典信号处理中的概念和⼯具（如平移，卷积，傅⾥叶变换，滤波器组和⼩波变换）扩展应⽤于任意⽹络中的数据5.加权图，有向图6.图在计算机的存储器中⽤矩阵表⽰，如邻接矩阵，关联矩阵，权重矩阵，度矩阵以及拉普拉斯矩阵等。
7.如果在两个节点之间存在多条边，称该图为多重图（multigraph）;如果存在⾃环，则称该图为伪图（pseudograph）8.包含原始图所有顶点的⼦图称为⽣成⼦图（spanning subgraph）9.图g的补图是指与图G具有同样的顶点集，但边集中的边则由那些在图g中不存在的边组成，也称为反向图（inverse graph）10.图在计算机中以矩阵或者链表的⽅式存储11.权重矩阵：图的权重矩阵包含图中相应边的权重。
权重矩阵是图的拓扑结构的完整表⽰。
所有的其他矩阵（邻接，度，拉普拉斯）都可以通过权重矩阵推导得出。
对于⾮加权图，权重矩阵和邻接矩阵是⼀样的。
12.邻接矩阵：包含图连接的N*N矩阵13.关联矩阵：每⼀⾏对应图中的⼀个顶点，⽽每⼀列对应图中的⼀条边。
14.度矩阵：是⼀个对⾓线矩阵，在对⾓线上包含了顶点的度。
节点的度是所有与该节点相关联的边的权重之和。
⼀些⼤的⽹络通常通过度的频率分布来刻画。
15.拉普拉斯矩阵：L=D-W，D是图的度矩阵，W是图的权重矩阵。
具有正边权重的⽆向图的拉普拉斯矩阵的基本性质:对称性；每⼀⾏之和为0，具有奇异性，det(L)=0；半正定；其特征值是⾮负实数。
16.归⼀化拉普拉斯矩阵：L(norm)=D(-1/2)LD^(-1/2)17.有向拉普拉斯矩阵：L=Din-W; Din是⼊度矩阵18.基本图测度：平均邻居度（AND），平均聚类系数（ACC，局部连通性属性），平均路径长度（APL，全局⽹络属性），平均边长度（AEL），图的直径和体积。
复杂网络基础理论第二章网络拓扑结构与静态特征第二章网络拓扑结构与静态特征l2.1 引言l2.2 网络的基本静态几何特征l2.3 无向网络的静态特征l2.4 有向网络的静态特征l2.5 加权网络的静态特征l2.6 网络的其他静态特征l2.7 复杂网络分析软件22.1 引言与图论的研究有所不同，复杂网络的研究更侧重于从各种实际网络的现象之上抽象出一般的网络几何量，并用这些一般性质指导更多实际网络的研究，进而通过讨论实际网络上的具体现象发展网络模型的一般方法，最后讨论网络本身的形成机制。
统计物理学在模型研究、演化机制与结构稳定性方面的丰富的研究经验是统计物理学在复杂网络研究领域得到广泛应用的原因；而图论与社会网络分析提供的网络静态几何量及其分析方法是复杂网络研究的基础。
32.1 引言静态特征指给定网络的微观量的统计分布或宏观统计平均值。
在本章中我们将对网络的各种静态特征做一小结。
由于有向网络与加权网络有其特有的特征量，我们将分开讨论无向、有向与加权网络。
4返回目录2.2 网络的基本静态几何特征¢2.2.1 平均距离¢2.2.2 集聚系数¢2.2.3 度分布¢2.2.4 实际网络的统计特征52.2.1 平均距离1.网络的直径与平均距离网络中的两节点v i和v j之间经历边数最少的一条简单路径（经历的边各不相同），称为测地线。
测地线的边数d ij称为两节点v i和v j之间的距离（或叫测地线距离）。
1／d ij称为节点v i和v j之间的效率，记为εij。
通常效率用来度量节点间的信息传递速度。
当v i和v j之间没有路径连通时，d ij＝∞，而εij＝0，所以效率更适合度量非全通网络。
网络的直径D定义为所有距离d ij中的最大值62.2.1 平均距离平均距离（特征路径长度）L定义为所有节点对之间距离的平均值，它描述了网络中节点间的平均分离程度，即网络有多小，计算公式为对于无向简单图来说，d ij＝d ji且d ii＝0，则上式可简化为很多实际网络虽然节点数巨大，但平均距离却小得惊人，这就是所谓的小世界效应。
72.2.1 平均距离2.距离与邻接矩阵的关系定义对于无权简单图来说，当l＝1时，。
容易证明无权简单图邻接矩阵A的l次幂A l的元素表示节点v i和v j之间通过l条边连接的路径数。
当l＝2时，容易推出式中，U表示单位指示函数，即当x＞0，U（x）＝1；否则U（x）＝0。
当i＝j时，δij＝1；否则δij＝0。
82.2.1 平均距离容易用数学归纳法证明据此，若D为网络直径，则两节点v i和v j之间的距离d ij可以表示为92.2.2 集聚系数首先来看节点的集聚系数定义。
假设节点v i与k i个节点直接连接，那么对于无向网络来说，这k i个节点间可能存在的最大边数为k i（k i－1）／2，而实际存在的边数为M i，由此我们定义C i＝2M i／［k i（k i－1）］为节点v i的集聚系数。
对于有向网络来说，这k i个节点间可能存在的最大弧数为k i（k i－1），此时v i的集聚系数C i＝M i／［k i（k i－1）］。
将该集聚系数对整个网络作平均，可得网络的平均集聚系数为102.2.2 集聚系数显然，0≤C≤1。
当C＝0，所有节点都是孤立节点，没有边连接。
当C＝1时，网络为所有节点两两之间都有边连接的完全图。
对于完全随机网络来说，当节点数很大时，C→O（1／N）。
而许多大规模的实际网络的集聚系数通常远小于1而大于O（1／N)。
对于社会网络来说，通常随着N→∞，集聚系数C→O（1），即趋向一个非零常数。
节点v i的集聚系数也可定义为C i＝N iΔ／N iΛ。
式中N iΔ代表与节点v i相连的“三角形”数目，数值上就等于M i；N iΛ代表与节点v i相连的“三元组”数目，即节点v i与其它两个节点都有连接，即“至少与其他两个分别认识”，数值上就等于k i（k i－1）／2。
112.2.2 集聚系数如何根据无向无权简单图的邻接矩阵A来求节点v i 的集聚系数C i？显然，邻接矩阵二次幂A2的对角元素表示的是与节点v i相连的边数，也就是节点v i的度k i。
而邻接矩阵三次幂A3的对角元素＝∑（a ij·a jl·a li）（j≠l）表示2.2.2 集聚系数【例2.1】计算下面简单网络的直径、平均距离和各节点的集聚系数。
解：首先计算出所有节点对的距离：d12＝1；d13＝1；d14＝2；d15＝1；d16＝2；d23＝1；d24＝1；d25＝2；d26＝2；d34＝2；d35＝2；d36＝1；d45＝3；d46＝1；d56＝3。
由此可得直径和平均距离为132.2.2 集聚系数下面以节点v1的集聚系数计算为例：采用第一种定义可知，节点v1与3个节点直接连接，而这3个节点之间可能存在的最大边数为3（3－1）／2，而实际存在的边数为1，由此可得C1＝2／［3（3－1）］＝1／3。
若采用第二种定义可知：与相连的三角形数为N1Δ＝１，而与v1相连的三元组数为N1Λ＝3，故C1＝1／3。
也可以利用式计算，因为邻接矩阵A的前三次幂为142.2.2 集聚系数故＝2，＝3，从而同理可得其他各节点的集聚系数为C2＝1／3；C3＝1／3；C4＝0；C5＝0；C6＝0由此很容易算出该网络的集聚系数152.2.3 度分布1.节点的度在网络中，节点v i的邻边数k i称为该节点v i的度。
对网络中所有节点的度求平均，可得到网络的平均度＜k＞无向无权图邻接矩阵A的二次幂A2的对角元素就是节点v i的邻边数，即。
实际上，无向无权图邻接矩阵A的第i行或第i列元素之和也是度。
从而无向无权网络的平均度就是A2对角线元素之和除以节点数，即＜k＞＝tr（A2）／N。
式中，tr（A2）表示矩阵A2的迹，即对角线元素之和。
162.2.3 度分布2.度分布大多数实际网络中的节点的度是满足一定的概率分布的。
定义P（k）为网络中度为k的节点在整个网络中所占的比率。
规则网络：由于每个节点具有相同的度，所以其度分布集中在一个单一尖峰上，是一种Delta分布。
完全随机网络：度分布具有Poisson分布的形式，每一条边的出现概率是相等的，大多数节点的度是基本相同的，并接近于网络平均度＜k＞，远离峰值＜k＞，度分布则按指数形式急剧下降。
把这类网络称为均匀网络。
无标度网络：具有幂指数形式的度分布：P（k）17∝k−γ。
所谓无标度是指一个概率分布函数F（x）对于2.2.3 度分布任意给定常数a存在常数b使得F（x）满足F（ax）＝bF（x）。
幂律分布是唯一满足无标度条件的概率分布函数。
许多实际大规模无标度网络，其幂指数通常为2≤γ≤3，绝大多数节点的度相对很低，也存在少量度值相对很高的节点（称为hub），把这类网络称为非均匀网络。
指数度分布网络：P（k）∝e−k/к，式中к＞0为一常数。
182.2.3 度分布3.累积度分布可以用累积度分布函数来描述度的分布情况，它与度分布的关系为它表示度不小于k的节点的概率分布。
若度分布为幂律分布，即P（k）∝k−γ，则相应的累积度分布函数符合幂指数为γ－1的幂律分布若度分布为指数分布，即P（k）∝e−k/к，则相应的累积度分布函数符合同指数的指数分布192.2.4 实际网络的统计特征20返回目录2.3 无向网络的静态特征¢2.3.1 联合度分布和度－度相关性¢2.3.2 集聚系数分布和聚－度相关性¢2.3.3 介数和核度¢2.3.4 中心性¢2.3.5 网络密度21¢2.3.6 连通集团（子图）及其规模分布2.3.1 联合度分布和度－度相关性1.联合度分布度分布满足平均度与度分布具有关系式联合度分布定义为从无向网络中随机选择一条边，该边的两个节点的度值分别为k 1和k 2的概率，即式中，M （k 1，k 2）为度值为k 1的节点和度值为k 2的节点相连的总边数，M 为网络总边数。
从联合度分布可以得出度分布式中，＝1（k ＝k 2）；＝0（k ≠k 2）。
222.3.1 联合度分布和度－度相关性联合节点度分布所包含的拓扑信息最多，节点度分布次之，平均节点度最少。
2.基于最近邻平均度值的度－度相关性度－度相关性描述了网络中度大的节点和度小的节点之间的关系。
若度大的节点倾向于和度大的节点连接，则网络是度－度正相关的；反之，若度大的节点倾向于和度小的节点连接，则网络是度－度负相关的。
节点v i的最近邻平均度值定义为式中，k i表示节点v i的度值，a ij为邻接矩阵元素。
232.3.1 联合度分布和度－度相关性所有度值为k的节点的最近邻平均度值的平均值k nn （k）定义为式中，N为节点总数，P（k）为度分布函数。
如果k nn（k）是随着k上升的增函数，则说明度值大的节点倾向于和度值大的节点连接，网络具有正相关特性，称之为同配网络；反之网络具有负相关特性，称之为异配网络。
3.基于Pearson相关系数的度－度相关性Newman利用边两端节点的度的Pearson相关系数r来描述网络的度－度相关性，具体定义为242.3.1 联合度分布和度－度相关性式中，k i，k j分别表示边e ij的两个节点v i，v j的度，M表示网络的总边数。
容易证明度－度相关系数r的范围为：0≤|r|≤1。
当r<0时，网络是负相关的；当r>0时，网络是正相关的；当r＝0时，网络是不相关的。
252.3.2 集聚系数分布和聚－度相关性1.集聚系数分布集聚系数分布函数P（C）表示从网络中任选一节点，其集聚系数值为C的概率式中，δ（x）为单位冲激函数。
2.聚－度相关性局部集聚系数C（k）定义为度为k的节点的邻居之间存在的平均边数＜M nn（k）＞与这些邻居之间存在的最大可能的边数的比值，即262.3.2 集聚系数分布和聚－度相关性全局集聚系数C则定义为式中，＜k2＞为度的二阶矩。
显然，局部集聚系数C（k）与k的关系刻画了网络的聚－度相关性。
许多真实网络如好莱坞电影演员合作网络、语义网络中节点的聚－度相关性存在近似的倒数关系C（k）∝k−1。
把这种倒数关系的聚－度相关性称为层次性，把具有层次性的网络称为层次网络。
272.3.3 介数和核度1.介数要衡量一个节点的重要性，其度值当然可以作为一个衡量指标，但又不尽然，例如在社会网络中，有的节点的度虽然很小，但它可能是两个社团的中间联络人，如果去掉该节点，那么就会导致两个社团的联系中断，因此该节点在网络中起到极其重要的作用。
对于这样的节点，需要定义另一种衡量指标，这就引出网络的另一种重要的全局几何量——介数。
介数分为节点介数和边介数两种，反映了节点或边在整个网络中的作用和影响力。
