图论入门

的度减去最小点的度，将最小点
的度设为0。
如果最后得到全0序列，则输出
yes，否则输出no
42 2
31
22 0
20
00 0
例题：给出一个非负整数组 成的有限序列s，s是否是某 个简单图的度序列？
332211 Yes
3331 No
首先利用图论第一定理。
然后把所有顶点排序，将最大点
的值设为0，然后将其后部最大点
在图G中，与顶点v相关联的边的总数 称为是v的度，记为deg v
图论第一定理
deg v 2m
vV (G)
证明：在计算G中所有顶点度的和时，每一条 边e被计数了两次。
例题：给出一个非负整数组 成的有限序列s，s是否是某 个图（无自环）的度序列？
242 Yes
31 No
首先利用图论第一定理。
然后把所有顶点排序，用最大点
图, 记 为G = (V, E ), 其中
① V称为G的顶点集, V≠, 其元素称为顶点或
结点, 简称点; ② E称为G的边集, 其元素称为边, 它联结V 中
的两个点, 如果这两个点是无序的, 则称该边为无 向边, 否则, 称为有向边.
如果V = {v1, v2, … , vn}是有限非空点集, 则称G 为有限图或n阶图.
如果某个有限图不满足(2)(3)(4),可在某条 边上增设顶点使之满足.
定义2 若将图G的每一条边e都对应一个实数F (e), 则称F (e)为该边的权, 并称图G为赋权图(网络), 记为G = (V, E , F ).
定义3 设G = (V, E)是一个图, v0, v1, …, vk∈V, 且1≤i≤k, vi-1vi∈E, 则称v0 v1 … vk是G的一条通路. 如果通路中没有相同的边, 则称此通路为道路. 始 点和终点相同的道路称为圈或回路. 如果通路中 既没有相同的边, 又没有相同的顶点, 则称此通路 为路径, 简称路.

第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理，图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.

end;
end;
end;
End； 15
End； End；
以上dfs(i)的时间复杂度为O（n*n）。 对于一个非连通图，调用一次dfs(i)，即按深度优先顺序依次访问了顶点i所在的（强）连通分支，所以 只要在主程序中加上：for i:=1 to n do {深度优先搜索每一个未被访问过的顶点}
if not Visited（I) then dfs(i);
Begin
访问顶点i；Visited[i]:=true;顶点i入队q；
while 队列q非空 do
begin
从队列q中取出队首元素v；
for j:=1 to n do
begin
if (not Visited[j]) and (a[v,j]=1) then
begin
时间：O（n*n）
访问顶点j；Visited[j]:=true;顶点j入队q
强连通分支：一个有向图的强连通分支定义为该图的最大的强连通子图， 右图含有两个强连通分支，一个是1和2构成的一个子图，一个是3独立构 成的一个子图。
7
图论算法与实现
一、图论基础知识
3、图的存储结构（n阶e条边）：
8
图论算法与实现
一、图论基础知识
4、图的遍历： 从图中某一顶点出发系统地访问图中所有顶点，使每个顶点恰好
11
图论算法与实现
一、图论基础知识
4、图的遍历： 图的宽（广）度优先遍历：类似于树的按层次遍历。从图中某个顶点V0出 发，访问此顶点，然后依次访问与V0邻接的、未被访问过的所有顶点，然 后再分别从这些顶点出发进行广度优先遍历，直到图中所有被访问过的顶 点的相邻顶点都被访问到。若此时图中还有顶点尚未被访问，则另选图中 一个未被访问过的顶点作为起点，重复上述过程，直到图中所有顶点都被 访问到为止。

常用虚线画出的闭合面表示割集。被每个虚线面切割 的边组成一个割集，如S1={a, c, e, g}，S2={b, c, e, g}等。
割集是图G所含边的一种最小集合。即只要少移去其中 一条边，图G仍将是连通的；另外，如果移去某些边后，使 图分成两个以上部分，此边集也不是割集。
2.1 图的基本概念
4、割集——割集的方向
对有向图，若给割集定义一个方向，则称为有向割集。 以表示割集的虚线面为界，可把从割集由内向外穿出的方 向定为割集的正方向，也可把从割集由外向内穿入的方向 定为正方向。 与割集方向相同的边，称为正向边；反之，称为负向 边。
2.1 图的基本概念
4、割集——生成树与割集的关系
一个连通图的生成树是连通这个图的全部节点的边数 最少的集合，而割集则是分割—个图的节点为不相连的二 个节点子集的边数最少的集合，因此，一个图的生成树与 割集间存在着一定的联系。 [定理] 连通图G的一个割集S至少包含图G的生成树的 一条树枝。因为单纯余树弦是不能将图G分成两部分的。
2.1 图的基本概念
1、图
图中节点的个数称为图的阶，用nv表示。每一对不 同节点间均有一条边相连的简单图称为完全图，图 G2就是一个4阶的完全图。m阶完全图的边数等于 v v e m(m-1)/2。 e v
1 9 1
e1 v2 e3 e5 v3
e2
4
1
v4
e4 e7
v2
e4 e3
v4
e5 e2 v3
2.1 图的基本概念
1、图
v2 v4 e4 e3 e2 v3
e9
v4 e5 e6 e8
v1
e1 v2
e7 e6 e2 e3 e4 v6 v3
e1

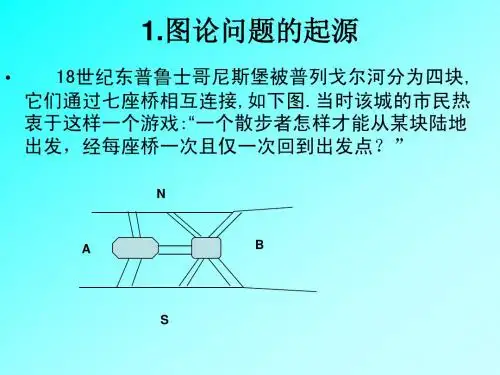
图论基本知识对于网络的研究，最早是从数学家开始的，其基本的理论就是图论，它也是目前组合数学领域最活跃的分支。

我们在复杂网络的研究中将要遇到的各种类型的网络，无向的、有向的、加权的……这些都可以用图论的语言和符号精确简洁地描述。

图论不仅为物理学家提供了描述网络的语言和研究的平台，而且其结论和技巧已经被广泛地移植到复杂网络的研究中。

图论，尤其是随机图论已经与统计物理并驾齐驱地成为研究复杂网络的两大解析方法之一。

考虑到物理学家对于图论这一领域比较陌生，我在此专辟一章介绍图论的基本知识，同时将在后面的章节中不加说明地使用本章定义过的符号。

进一步研究所需要的更深入的图论知识，请参考相关文献[1-5]。

本章只给出非平凡的定理的证明，过于简单直观的定理的证明将留给读者。

个别定理涉及到非常深入的数学知识和繁复的证明，我们将列出相关参考文献并略去证明过程。

对于图论知识比较熟悉的读者可以直接跳过此章，不影响整体阅读。

图的基本概念图G 是指两个集合(V ，E)，其中集合E 是集合V×V 的一个子集。

集合V 称为图的顶点集，往往被用来代表实际系统中的个体，集合E 被称为图的边集，多用于表示实际系统中个体之间的关系或相互作用。

若{,}x y E ，就称图G 中有一条从x 到y 的弧（有向边），记为x→y ，其中顶点x 叫做弧的起点，顶点y 叫做弧的终点。

根据定义，从任意顶点x 到y 至多只有一条弧，这是因为如果两个顶点有多种需要区分的关系或相互作用，我们总是乐意在多个图中分别表示，从而不至于因为这种复杂的关系而给解析分析带来困难。

如果再假设图G 中不含自己到自己的弧，我们就称图G 为简单图，或者更精确地叫做有向简单图。

以后如果没有特殊的说明，所有出现的图都是简单图。

记G 中顶点数为()||G V ν=，边数为()||G E ε=，分别叫做图G 的阶和规模，显然有()()(()1)G G G ενν≤-。

图2.1a 给出了一个计算机分级网络的示意图，及其表示为顶点集和边集的形式。

第6章图论一、内容提要1.图的定义定义1.(图的定义一)图G = (V, E)是一个系统，其中(1)V≠∅是一个有限集合；V中的每一元素v∈V都称为图G的一个结点；V称为图G 的结点集；(2)E是一个有限集合；E中的每一元素e∈E都称为图G的一条边；E称为图G的边集。

定义2. (图的定义二)图G = (V, E)是一个系统，其中(1)V ≠∅是一有限集合；V中的每一元素v∈V都称为图G的一个结点；V称为图G的结点集；(2)E⊆V⨯V是一有限集合，一个V上的关系；E中的每一元素(u,v)∈E都称为图G的一条边(这里u, v∈V)；E称为图G的边集。

定义3. (图的定义三)图G= (V,∑, E)是一个系统，其中(1)V ≠∅是一有限集合；V中的每一元素v∈V都称为图G的一个结点；V称为图G的结点集；(2)∑是一有限集合；∑中的每一元素σ∈∑都称为图G中的一个标号；∑称为图G的标号集；(3)E ⊆V⨯∑⨯V是一有限集合，一个三元关系；E中的每一元素(u,σ ,v)∈E都称为图G的一条边或弧,此边起自u而终于v；称u是此边的起点，称σ是此边的标号，称v是此边的终点，起点和终点统称为边的端点(这里u, v∈V , σ∈∑)；E称为图G的边集。

定义4. (图的定义四)图G=(V,E, γ)是一个系统，其中(1)V ≠∅是一有限集合；V中的每一元素v∈V都称为图G的一个结点；V称为图G 的结点集；(2)E是一个有限集合；E中的每一元素e∈E都称为图G的一条边；E称为图G的边集。

(3)γ是边到结点集的一个关联函数，即γ:E→2V(无向图) 或γ:E→ V⨯V (有向图) 。

一般来说，它将E中的每条边e∈E与结点集V中的一个二元子集{u,v}∈2V (或{u,v}⊆V)相关联或与结点集V上的一个二元组(u,v)∈V⨯V相关联，即γ(e)={u,v} (无向图) 或γ(e)= (u,v) (有向图) ，称u是此边的起点，称v是此边的终点，结点u和v统称为边的端点。

常州市第一中学 林厚从
图论算法与实现
一、图论基础知识
4、图的遍历： 对下面两个图分别进行深度优先遍历，写出遍历结果。 注意：分别从a和V1出发。
左图从顶点a出发，进行深度优先遍历的结果为：a，b，c，d，e，g，f 右图从V1出发进行深度优先遍历的结果为：V1，V2，V4，V8，V5，V3，V6，V7
邻接矩阵
边集数组
邻接表
优点O（1）
存储稀疏图时，空 间效率比较好，也 比较直观
便于查找任一顶点的关联边及 关联点,查找运算的时间复杂 性平均为O(e/n)
存储稀疏图，会造 成很大的空间浪费
不适合对顶点的运 算和对任意一条边 的运算
要查找一个顶点的前驱顶点和以此顶点 为终点的边、以及该顶点的入度就不方 便了，需要扫描整个表，时间复杂度为O （n+e）。可以用十字邻接表改进
被访问一次，这种运算操作被称为图的遍历。为了避免重复访问某个 顶点，可以设一个标志数组visited[i]，未访问时值为false，访问一次 后就改为true。
图的遍历分为深度优先遍历和广度（宽度）优先遍历两种方法。 图的深度优先遍历：类似于树的先序遍历。从图中某个顶点Vi出发， 访问此顶点并作已访问标记，然后从Vi的一个未被访问过的邻接点Vj出 发再进行深度优先遍历，当Vi的所有邻接点都被访问过时，则退回到上 一个顶点Vk，再从Vk的另一个未被访问过的邻接点出发进行深度优先遍 历，直至图中所有顶点都被访问到为止。
常州市第一中学 林厚从
图论算法与实现
一、图论基础知识
4、图的遍历： 对于一个连通图，深度优先遍历的递归过程如下：
Procedure dfs(i:integer)； {图用邻接矩阵存储} Begin
访问顶点i； Visited[i]:=True； For j:=1 to n do {按深度优先搜索的顺序遍历与i相关联的所有顶点}

内容摘要
这一章通过分析图的连通性，让读者理解图中的信息流动和路径问题。 第四章介绍了图的遍历算法，包括深度优先遍历和广度优先遍历。这两种算法是常用的图遍历算 法，通过这一章的学习，读者可以掌握如何遍历一个图并获取所需信息。 第五章介绍了最小生成树算法，包括Prim算法和Kruskal算法。这两种算法是最常用的最小生成 树算法，通过这一章的学习，读者可以掌握如何找到一个图中连接所有节点的最小代价的树。 第六章介绍了拓扑排序算法，包括Kahn算法和DFS算法。拓扑排序是解决有向无环图（DAG）上 的一种排序算法，通过这一章的学习，读者可以掌握如何对一个有向无环图进行拓扑排序。 《程序员的数学4：图论入门》这本书是一本非常适合程序员阅读的数学书籍，它介绍了图论的 基本概念和应用，并提供了很多实例和练习题帮助读者理解和应用所学知识。这本书不仅可以提 高程序员的数学素养，还可以帮助程序员更好地理解和应用图论来解决实际问题。
精彩摘录
精彩摘录
《程序员的数学4：图论入门》是一本面向程序员群体的数学入门指南，其作 者罗博·福布斯将带大家探索图论的基础概念和算法，从而更好地理解和应用编 程技术。本书将选取一些精彩的摘录，供大家欣赏。
精彩摘录
“图论是一个研究图形和结构的学科，其中节点和边分别表示对象和它们之 间的关系。”
精彩摘录
这是本书最基本的概念之一，通过节点和边这两个概念，我们可以描述各种 复杂的结构。在编程中，我们通常会使用节点和边来表示数据结构，例如树、图 等。
精彩摘录
“一个图G=(V,E)由一组节点V和一组边E组成。”
精彩摘录
这个定义简洁明了，很好地概括了图论的基本构成要素。在许多应用场景中， 节点可以表示人、物体或其他实体，而边则表示这些实体之间的关系。

深度优先搜索
• 深度优先搜索运用递归的方法。进入一个点以后，就把这个点 当做新的起点继续搜索下去，一直到无路可走。 void dfsvis(int u) { int i; for(i=0;i<n;i++) if(num[u][i]!=0 && vis[i] == 0) dfs(i); vis[a]=1; }
数组版邻接表
• Void addedge(int u,int v,int c){ e++; // 全局变量，代表已经插入的边数 nxt[e]=head[u]; pnt[e]=v;cost[e]=c; head[u]=e; //和链表的思路完全一样！！ } 推荐大家用这种方法！！省时！！
一些建议
• 第一，记得初始化。 • 第二，不要用graph[1000]这种方式建数组。要用宏 定义或者const，这样方便改。 • 第三，认真辨别有向图或者无向图，对于无向图需 要加两次边。 • 第四，要尽量运用全局变量。
图的存储方式
• 1. 邻接矩阵 • 实现方法： 二维数组 • 如果u，v之间有一条权值为c的边，那么对有向图， 加边的操作就是graph[u][v]=c。对无向图，必须再加 上graph[v][u]=c。 • 优点：好操作，找边方便。 • 缺点：不能有重边，存储空间有很多浪费的。
知识普及：链表
• 链表是完全不同于数组的一种线性结构，它的特点 就是存储空间是随机的，只能一个指着一个。如果 想找到a，就必须先找到指向a的那个节点！ • 初始化： struct edge{ int to,cost; edge *next; } • 结构体edge中有一个指向edge类型的指针，就是这 样。
• • • • • • • • void addedge(int u,int v,int cost){ edge p=new(edge); p->cost=cost;p->to=v; p->next=graph[u].next; graph[u].next=p; } 注意：每次建图前要初始化，把next设置成NULL。 要熟练运用指针！！！

vV1
deg(v) deg(v) 2 E
vV2
图的同构
• 试观察下面各图有何异同
• • • • •
根据图的同构定义，可以给出图同构的必要条件如下： (1) 结点数目相等； (2) 边数相等； (3) 度数相同的结点数目相等。 但这仅仅是必要条件而不是充分条件。
• 上图中的(a)和(b)满足上述三个条件，然而并不同构。 • 因为在(a)中度数为3的结点x与两个度数为1的结点邻接， 而(b)中度数为3的结点y仅与一个度数为1的结点邻接。 • 寻找一种简单有效的方法来判定图的同构，至今仍是图论 中悬而未决的重要课题。 • 对于同构，形象地说，若图的结点可以任意挪动位置，而 边是完全弹性的，只要在不拉断的条件下，这个图可以变 形为另一个图，那么这两个图是同构的。故同构的两个图 从外形上看可能不一样，但它们的拓扑结构是一样的。
• ii) 存在唯一的 Ｇ１∪Ｇ２和 Ｇ１ Ｇ２。
• 证明：以 i) 为例，不妨设 G １和Ｇ２同为有向图，若同为无向图也 可同样证明。 • a) （存在性）
•
• • • • • 交
定义 Ψ ：E1∩Ｅ２→ (V1∩V2)× (V1∩V2) 为 ：
对于任意的 e∈Ｅ１∩Ｅ２，Ψ (e) ＝ Ψ １(e) ＝ Ψ ２(e) 。 显然，〈Ｖ１∩Ｖ２，Ｅ１∩Ｅ２，Ψ 〉＝ Ｇ１∩Ｇ２。 b) （唯一性） 设图 G＝〈Ｖ１∩Ｖ２，Ｅ１∩Ｅ２，Ψ 〉 和 G＝〈Ｖ１∩Ｖ２，Ｅ１∩Ｅ２，Ψ 〉均为 G１和Ｇ２的 。 G1，所以对任意 e∈E1∩E2 皆有 Ψ (e) ＝Ψ 1(e) 。
v)
vi)
Ｇ1∪Ｇ2
Ｇ1 Ｇ2
=
=
〈V1∪Ｖ2，Ｅ1∪Ｅ2，Ψ 1∪Ψ 2〉

图论基础：图的基本概念和应用图论是数学中的一个分支领域，研究的是图的性质和图上的问题。

图被广泛应用于计算机科学、电子工程、运筹学、社交网络分析等领域。

本文将介绍图论的基本概念和一些常见的应用。

一、图的基本概念1. 顶点和边图是由顶点和边组成的，顶点代表图中的元素，边则代表元素之间的关系。

通常顶点表示为V，边表示为E。

2. 有向图和无向图图可以分为有向图和无向图。

在无向图中，边是没有方向的，顶点之间的关系是双向的；而在有向图中，边是有方向的，顶点之间的关系是单向的。

3. 权重在一些应用中，边可能具有权重。

权重可以表示顶点之间的距离、成本、时间等概念。

有权图是指带有边权重的图，而无权图则是指边没有权重的图。

4. 路径和环路径是指由一系列边连接的顶点序列，路径的长度是指路径上边的数量。

环是一种特殊的路径，它的起点和终点相同。

5. 度数在无向图中，顶点的度数是指与该顶点相关联的边的数量。

在有向图中分为出度和入度，出度是指从该顶点出去的边的数量，入度是指指向该顶点的边的数量。

二、图的应用1. 最短路径问题最短路径问题是图论中的一个经典问题，它研究如何在图中找到两个顶点之间的最短路径。

这个问题有许多实际应用，例如在导航系统中寻找最短驾驶路径，或者在电信网络中找到最短的通信路径。

2. 最小生成树最小生成树是指一个连接图中所有顶点的无环子图，并且具有最小的边权重之和。

这个概念在电力网络规划、通信网络优化等领域有广泛的应用。

3. 路由算法在计算机网络中，路由算法用于确定数据包在网络中的传输路径。

图论提供了许多解决路由问题的算法，如最短路径算法、Bellman-Ford 算法、Dijkstra算法等。

4. 社交网络分析图论在社交网络分析中起着重要的作用。

通过构建社交网络图，可以分析用户之间的关系、信息传播、社区发现等问题。

这些分析对于推荐系统、舆情监测等领域具有重要意义。

5. 电路设计图论在电路设计中也有应用。

通过将电路设计问题转化为图论问题，可以使用图论算法解决电路布线、最佳布局等问题。

基本知识点：一、图的基本定义：平凡图：只有一个顶点无边的图。

非平凡图：其他所有图。

空图：边集合为空的图。

简单图：既没有环也没有重边的图。

复合图：其他所有的图。

同构图：顶点集合之间存在双射（一一对应关系），对应边重数和端点对应相等。

标定图：给图的点和边标上符号。

非标定图：不标号。

非标定图代表一类相互同构的图。

完全图：每两个不同顶点之间都有一条边相连的简单图。

N 个顶点的完全图只有一个，记为n K 。

偶图（二部图）：具有二分类(,)X Y 的图，他的点集可以分解为两个（非空）子集X 和Y ，使得每条边的一个端点在X 中，另一个端点在Y 中。

完全偶图 ：指具有二分类(,)X Y 的简单偶图，其中X 的每个顶点与Y 的每个顶点相连。

若,X m Y n ==，则这样额完全偶图记为：,m n K 。

k —正则图：设(,)G V E =为简单图，如果对所有的结点v V ∈，有()d v k =，称G 为k —正则图。

完全图和完全偶图,n n K 均是正则图。

图划分：若一个n 阶简单图G 各点的度为i d ，则分正整数k 为n 个部分的划分i d ∑称为是图划分。

子图：边集合和点集合均是原图的子集，且待判定图中的边的重数不超过原图中对应的边的重数。

生成子图：点集合相等，边集合为原图子集的图。

导出子图：由顶点集为原图G 真子集的所有点，及两端点均在该集合中的边的全体组成的子图V ‘。

'[]G V 和G v -。

边导出子图：由原图G 边的真子集，该图中边的断点全体为顶点组成的子图E ‘。

'[]G E 和{}G e -。

图的运算：并，交，差，对称差，联图，积图，合成图，极图路与图的联通性：途径：迹：边互不相同的途径。

路：边和点都互不相同的途径。

连通的：两个顶点之间存在路。

连通图：每一对顶点之间都有一条路。

连通分支：将V 划分为一些等价类12,,...k V V V 。

两个顶点u 和v 是连通的当且仅当他们属于同一个子集i V ，称子图()i G V 为连通分支。

离散数学中的图论入门图论是离散数学的一个重要分支，研究的对象是图。

图是由一些点和连接这些点的边组成的数学模型，可以用来描述现实世界中的各种关系和问题。

本文将介绍图论的基本概念和常见应用，帮助读者初步了解图论的入门知识。

一、图的定义与基本术语图由顶点集合和边集合组成。

顶点集合是图中的点的集合，用V表示；边集合是图中连接顶点的边的集合，用E表示。

图可以分为有向图和无向图。

有向图中的边是有方向的，表示从一个顶点指向另一个顶点的关系；无向图中的边是无方向的，表示两个顶点之间的关系。

图还可以分为简单图和多重图。

简单图中不存在重复的边和自环（起点和终点相同的边）；多重图中可以存在重复的边和自环。

图中的边可以带权重，表示顶点之间的距离、代价或其他属性。

带权图可以用来解决最短路径、最小生成树等问题。

图的度是指与顶点相关联的边的数量。

对于无向图，顶点的度等于与之相连的边的数量；对于有向图，顶点的度分为入度和出度，分别表示指向该顶点的边的数量和从该顶点指出的边的数量。

二、图的表示方法图可以用邻接矩阵和邻接表两种方式进行表示。

邻接矩阵是一个二维数组，其中的元素表示两个顶点之间是否存在边。

如果顶点i和顶点j之间存在边，则邻接矩阵中第i行第j列的元素为1；否则为0。

邻接矩阵适用于稠密图，但对于稀疏图来说，会浪费较多的存储空间。

邻接表是由若干个链表构成的数组，数组的每个元素对应一个顶点，链表中存储与该顶点相连的其他顶点。

邻接表适用于稀疏图，可以有效地节省存储空间。

三、常见的图论算法与应用1. 深度优先搜索（DFS）：DFS是一种用于遍历图的算法，通过递归的方式依次访问与当前顶点相邻的未访问过的顶点，直到所有顶点都被访问过为止。

DFS可以用来解决连通性、可达性等问题。

2. 广度优先搜索（BFS）：BFS也是一种用于遍历图的算法，通过队列的方式按层次遍历图中的顶点。

BFS可以用来求解最短路径、网络分析等问题。

3. 最小生成树（MST）：最小生成树是指在连通图中选择一棵生成树，使得树中所有边的权重之和最小。

树支：组成树的支路。 树支数 nt n 1
连支：其余的支路。 连支 数 l b nt b n 1
第9页/共13页
X
2. 图论的一些基本概念
树支电压，连支电流
树支集合 2，5，6 连支集合 1，3，4
1
①
2② 3
③
5
4
6
④
2.9 基本回路：只含有一条连支的回路。
注
１，6，5，2 3，6，5 4，2，5
①
①
①
1
3
2
1 2
1
3
② 4③ 5 ④ ② 4 ③5 ④ ② 4③ 5 ④
图G
子图 G1
子 G2
图
第8页/共13页
X
2. 图论的一些基本概念
2.8 树(tree-T) ：树是连通图G的一个连通子图；包含
图G的所有的节点；不包含任何回路。
①
①
①
1
3
2
1
3
2
1
② 4③5 ④ ②
③
4
5
④②
③④
图G
T1
T2
2.1 拓扑(topology)：几何或联接性质。
2.2 图(Graph):电路（网络）的图由支路（线段）和节 点（点）组成，用G表示。每一支路代表一个电路元件 或一些电路元件的某种组合，每一支路都连接在图中 的两个节点之间。
标准支 ①
②①
②
路组合
i
u
第4页/共13页
X
2. 图论的一些基本概念
第5页/共13页
X
2. 图论的一些基本概念
2.4 路径(path)：从图G的某一节点出发，沿着一些支

第一节 图论基本知识
一、图的基本概念
1、图的表示
G G(V , E ), 其中V V (G )为顶点集， E (G ) E 为边集， e E , e联结V中两个顶点。
有向图：边均有方向无向 图：边均 无方 向
2、V中顶点 与v间有一条边，则称 v相邻， u u与 u, v , e相关联，与顶点关联的边数称为的度， u u 记为d ( u).
5、定理2 下列命题是等价的
(1)G是树
(2)G中任两顶点之间有且仅 有一条路相通
(3)G中无圈，且 (G) V (G) 1 E
(4)G连通，且 (G) V (G) 1 E
(5)G连通，且 中任意去掉一条边后不 G 连通
(6)G无圈，而 加上一条不在 (G )中的边后 G E 恰有一个圈
在 图G中 ，V (G ) X Y , X Y , X Y 0 且E (G )中 每 一 边 的 两 个 顶 点 是 一 个 在 中 ， 都 X 一个在 中。 Y
3、定理1 一个图是二部图 它不包含奇数条边的圈 4、森林，树
பைடு நூலகம்
若 一 个 图 是 无 圈 的 ，称 为 森 林 ； 若 它 又 是通 的 ， 则 连 则称为树
n阶方阵，称为 的邻接矩阵：(G) (aij ) G A
1, v i 与v j 相 邻 aij 0, v i 与v j 不 相 邻
注意： 邻接矩阵每一行中 的个数为相应顶点的度 1 数。
三、一些特殊图
1、完全图
图中任两个顶点均有边 相邻。常记为 n , n V K
2、二部图（偶图）
n m的 关 联 矩 阵 (G ) : 每 一 行 对 应 中 的 一 个 顶 点 ， M V 每 一 列 对 应 中 一 条 边 ， 当i 与ei 相 关 联 时 ， (G ) E v M 中i行j列 元 素 为， 否 则 为。 1 0

时间复杂度: O(n+m) 定理: 无向图只有T边和B边 (易证)
实现细节
1. if (d[v] == -1) dfs(v);
//树边, 递归遍历
2. else if (f[v] == -1) show(“B”); //后向边
3. else if (d[v] > d[u]) show(“F”); // 前向边
3. begin read(n); for i:=1 to n do begin new(head[i]); head[i]^.key:=i; head[i]^.next:=nil; end; read(m); s:=0; for i:=1 to m do begin read(edgex[i],edgey[i]); new(p); p^.key:=edgey[i]; p^.next:=head[edgex[i]]; head[edgex[i]]:=p; end; fillchar(f,sizeof(f),true); fillchar(instack,sizeof(instack),false); top:=0;time:=0; for i:=1 to n do if f[i] then tarjan(i); fillchar(s1,sizeof(s1),0);
非连通图有多个连通分量(connected component, cc), 每个连通分量是一个 极大连通子图(maximal connected subgraph)
完全图和补图
完全图:N个顶点的图，有N(N-1)/2个节点 对于(u,v), 若邻接则改为非邻接, 若非邻接则改为邻接, 得到的图为原图的补
int j; DFN[i]=LOW[i]=++Dindex; instack[i]=true; Stap[++Stop]=i; for (edge *e=V[i];e;e=e->next) {

代码（复杂度n2）
堆优化
• 在Dij算法的过程中，d[i] =min(d[i],d[v]+w(v,i)) for i in T 这个操作是O(n) 的 • 这个操作可以用优先队列优化，每次直接 弹出最小的即可 • 更新的过程也是O(n)，用领接表的话会优化。
• 模板 • /25184337/
Bellman_foห้องสมุดไป่ตู้d算法
• Dij算法只能对于正权图 如果边的权值为负数，那么这个就没用 了 • 先规定：如果存在负圈，那么s->u的最短路是负无穷 • 算法步骤：
• 1.初始化：将除源点外的所有顶点的最短距离估计值 d[v] ← +∞, d[s] ←0; • 2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点 集V中的每个顶点v的最短距离估计值逐步逼近其最短距离； （运行|v|-1次） • 3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。 如果存在未收敛的顶点，则算法返回false，表明问题无解；否 则算法返回true，并且从源点可达的顶点v的最短距离保存在 d[v]中。
图论 入门
最小生成树 最短路
这是前（废）言（话）
• 多校可以做做 被虐是正常的（手动滑稽）
• 互相可以多多交流 学习一下AC的姿势 这样 可以提高自己的姿势水平 • 上课不是全部
图
• 节点 边 • 有向图 无向图
存储方式
• 1 二维数组 • Int Map[maxn][maxn] • 2 vector const int maxn=1e5+10; vector<int> g[maxn]; void addedge(int u,int v){g[u].push_back(v);} vector写起来比较简单，但是在一些对内存卡 的很严的题有可能会被卡