下载文档原格式
数学中的图论与网络知识点图论是数学中一个重要的分支领域，研究图的结构、性质以及与实际问题的应用。
而网络则是现代社会中的重要组成部分，图论在网络上的应用也日益广泛。
本文将介绍数学中的图论基本概念和网络知识点，以及它们在现实中的应用。
一、图论基本概念1. 图的定义与表示图是由节点（顶点）和边组成的一种数学结构。
节点表示对象，边表示节点之间的连接关系。
图可以用邻接矩阵或邻接表等方式进行表示与存储。
2. 图的分类图可以分为有向图和无向图。
有向图中的边有方向，无向图中的边没有方向。
根据边是否具有权重，图又可以分为带权图和无权图。
3. 图的性质图具有很多重要的性质，例如连通性、度、路径等。
连通性表示图中任意两个节点之间存在一条路径，度表示节点的相邻节点个数，路径是连接节点的边的序列。
二、图论中的常见算法1. 最短路径算法最短路径算法用于求解两个节点之间的最短路径，其中最著名的算法是Dijkstra算法和Floyd-Warshall算法。
Dijkstra算法适用于边权重为非负的图，而Floyd-Warshall算法适用于任意带权图。
2. 深度优先搜索与广度优先搜索深度优先搜索（DFS）和广度优先搜索（BFS）是图的遍历算法。
DFS以深度优先的方式探索图中的节点，BFS以广度优先的方式探索。
这两种算法在解决连通性、拓扑排序等问题中有广泛应用。
3. 最小生成树算法最小生成树算法用于在带权图中找到权重和最小的生成树。
其中Prim算法和Kruskal算法是两种常用的最小生成树算法。
三、网络中的图论应用1. 社交网络与关系分析社交网络是图的一种应用，其中节点表示人，边表示人与人之间的社交关系。
基于图论的算法可以分析社交网络中的社区结构、关键人物等信息。
2. 网络流与最大流问题网络流是指在图中模拟流动的过程，最大流问题是求解从源节点到汇节点的最大流量。
网络流算法可以用于优化问题的求解，如分配问题、进程调度等。
3. 路由算法与网络优化路由算法是网络中常用的算法之一，用于确定数据从源节点到目的节点的传输路径。
网络图论图论是数学的一个分支，是富有趣味和应用极为广泛的一门学科。
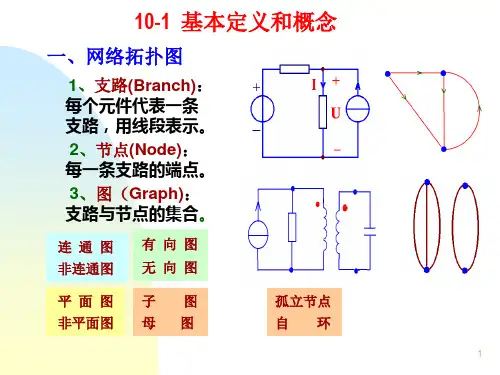
(1)图图(a)电路，如果用抽象线段表示支路则得到图(b)所示的拓扑图，它描述了电路的点和线的连接关系，称为电路的图。
定义：图G 是描述电路结点支路连接关系的拓扑图，它是支路和结点的集合。
1）支路总是连接于两个结点上。
2）允许孤立结点存在，不允许孤立的支路存在。
移走支路，该支路连接的两个结点要保留在电路中，而移走结点，则要将连接于该结点的所有支路移走。
电路的图是用以表示电路几何结构的图形，图中的支路和结点与电路的支路和结点一一对应。
9.1 网络图论的基本概念(3)有向图：标示了参考方向的图(2)子图：图G1中的所有支路和结点都是图G中的支路和结点，则称G1是G 的一个子图。
子图示例9.1 网络图论的基本概念(4)连通图图中任何两结点之间存在由支路构成的路径，则称为连通图。
连通图和非连通图示例9.1 网络图论的基本概念(5)回路从某个结点出发，经过一些支路(一条支路仅经过一次)和一些结点(每个结点仅经过一次)又回到出发点所经闭合路径。
树和非树示例(6)树G1是G 的一个子图，且满足以下三个条件：A 、是连通的；B 、包含G 中所有结点；C 、不包含回路。
G1称为G 的一棵树。
9.1 网络图论的基本概念(7)树支、树支数构成树的支路称为树支。
树支数为：割集示例(8)连支、连支数不属于树的支路称为连支。
连支数为：(9)割集、割集方向移走某些支路，图分成了两个分离的部分，则这些支路的集合称为割集。
割集的方向：从一部分指向另一部分的方向。
9.2 关联矩阵、回路矩阵、割集矩阵、及KCL和KVL方程的矩阵形式(1)增广矩阵描述图中结点和支路关联情况的矩阵。
矩阵元素：增广矩阵为n×b 阶矩阵。
图9.2.1图的增广矩阵：9.2.1 关联矩阵A9.2 关联矩阵、回路矩阵、割集矩阵、及KCL 和KVL方程的矩阵形式(2)关联矩阵A增广矩阵每一列对应一条支路，非零元素两个，一个是1一个是-1，表示1号支路从1号结点流向2号结点；每一行代表一个结点，如第1行表示支路1、4、6连在1号结点，且支路1从1号结点流出，支路4流入1号结点，支路6流出1号结点。
题目: 矩阵论在电气工程中的应用指导老师: xxx学生姓名：xxx所属院系：电气工程学院专业：电气工程学号：xxx完成日期：20xx年x月x日矩阵论在电气工程中的应用摘要电路分析是电气专业领域人员必需的一项能力。
该知识具有概念性强、电路分析繁杂求解计算量大的特点。
为了解决这个问题，因此引入了矩阵理论，并结合软件对矩阵分析的良好支持，以期达到优化分析电路的目的。
本文就矩阵理论中的网络拓扑知识展开，介绍了网络拓扑在电路中的应用，并以给予求解。
关键词：电路分析矩阵法网络拓扑ABSTRACT：Circuit analysis is an essential ability of professional personnel in the field of electronic. The concept of strong, complex circuit analysis calculation with the knowledge of the characteristics of large amount. In order to alleviate this problem, so we introduced matrix theory, combined with good support analysis software for matrix, in order to achieve the purpose of optimization of circuit analysis. In this paper, the network topology in matrix theory unfolds, introduces the application of network topology in circuit, and to give the solution.KEY WORDS：circuit analysis；matrix method；network topology0 前言矩阵是线性代数里的一个重要概念，在电路网络分析、工程结构分析等方面，矩阵都是一个强自力的工具，因为它能使较复杂的计算过程简化成一系列的四则运算，便于用计算机的算法语言或程序进行描述和解答。
电网络分析综述电路CAD技术是电路分析、设计、验证的有力工具，随着集成电路特征尺寸进入纳米时代，电路的规模越来越大，工作频率越来越高，芯片上市时间越来越短，以集成电路CAD为基础的电子设计自动化(EDA)已经成为提高设计效率、优化电路性能，增加芯片可靠性和提高芯片合格率的新兴产业，渗入到集成电路设计的每一阶段。
电路CAD已经有近40年的历史，涉及电路理论、半导体器件物理、线性与非线性方程组的求解方法、最优化涉及、数值分析和计算机软件等多个领域。
纳米时代的到来既为电路CAD技术带来了机遇，也使之前面临更大的挑战。
随着集成电路与计算机的迅速发展，以电子计算机辅助设计为基础的电子设计自动化技术已经成为电子学领域的重要学科，并已形成一个独立的产业。
它的兴起与发展，又促进了集成电路和电子系统的迅速发展。
当前，集成电路的集成度越来越高，电子系统的复杂程度日益增大，而电子产品在市场上所面临的竞争却日趋激烈，产品在社会上的收益寿命越来越短，甚至只有一二年时间。
处于如此高速发展和激烈竞争的电子世界，电路设计工作者必须拥有强大有力的EDA 工具才能面对各种挑战，高效地创造出新的电子产品。
20世纪70年代到80年代初期，电子计算机的运算速度、存储量和图形功能还正在发展之中，电子CAD和EDA技术还没有形成系统，仅是一些孤立的软件程序。
这些软件在逻辑仿真、电路仿真和印刷电路板(PCB)、IC版图绘制等方面取代了设计人员靠手工进行繁琐计算、绘图和检验的方式，大大提高了集成电路和电子系统的设计效率和可靠性。
但这些软件一般只有简单的人机交互能力，能处理的电路规模不是很大，计算和绘图的速度都受限制。
而且由于没有采用统一的数据库管理技术，程序之间的数据传输和交换也不方便。
20世纪80年代后期，是计算机与集成电路高速发展的时期，也是EDA技术真正迈向自动化并形成产业的时期。
这一阶段，EDA的主要特点是：能够实现逻辑电路仿真、模拟电路仿真、集成电路的布局和布线、IC版图的参数提取与检验、印制电路板的布图与检验、以及设计文档制作等各设计阶段的自动设计，并将这些工具集成为一个有机的EDA系统，在工作站或超级微机上运行。
.题目: 矩阵论在电气工程中的应用指导老师: xxx学生姓名：xxx所属院系：电气工程学院专业：电气工程学号：xxx完成日期：20xx年x月x日矩阵论在电气工程中的应用摘要电路分析是电气专业领域人员必需的一项能力。
该知识具有概念性强、电路分析繁杂求解计算量大的特点。
为了解决这个问题，因此引入了矩阵理论，并结合软件对矩阵分析的良好支持，以期达到优化分析电路的目的。
本文就矩阵理论中的网络拓扑知识展开，介绍了网络拓扑在电路中的应用，并以给予求解。
关键词：电路分析矩阵法网络拓扑ABSTRACT：Circuit analysis is an essential ability of professional personnel in the field of electronic. The concept of strong, complex circuit analysis calculation with the knowledge of the characteristics of large amount. In order to alleviate this problem, so we introduced matrix theory, combined with good support analysis software for matrix, in order to achieve the purpose of optimization of circuit analysis. In this paper, the network topology in matrix theory unfolds, introduces the application of network topology in circuit, and to give the solution.KEY WORDS：circuit analysis；matrix method；network topology0 前言矩阵是线性代数里的一个重要概念，在电路网络分析、工程结构分析等方面，矩阵都是一个强自力的工具，因为它能使较复杂的计算过程简化成一系列的四则运算，便于用计算机的算法语言或程序进行描述和解答。
