计算机图形学_ 三维图形变换_

三维图形变换是在二维方法基础上增加了对z坐标的考虑得到的。

与二维变换类似，引入齐次坐标表示，即：三维空间中某点的变换可以表示成点的齐次坐标与四阶的三维变换矩阵相乘。

一、平移变换二．比例变换例如：对长方体进行比例变换，三、旋转变换跟二维的相同四、对称变换有关于坐标平面、坐标轴的对称变换（1）关于坐标平面的对称绕哪个面变换，那个面不变变换矩阵为：其它均类似（2）关于坐标轴变换6.2 投影变换投影变换就是把三维物体投射到投影面上得到二维平面图形两种投影法的本质区别在于：透视投影的投影中心到投影面之间的距离是有限的；而另一个的距离是无限的。

一、中心（透视）投影特点：投影线均通过投影中心，物体的投影视图由计算投影线与观察平面交点而得在投影中心相对投影面确定的情况下，空间的一个点在投影面上只存在唯一一个投影。

透视投影生成真实感视图，但不保证相关比例。

二、平行投影1、把透视投影的中心移至无穷远处，则各投影线称为相互平行的直线，这种投影2、分为正投影和斜投影3、特点：保持物体的有关比例不变三、平面集合投影的分类6.3 三视图一、1、根据投影面与坐标轴的夹角可分为两类：三视图和正轴侧图。

当投影面与某一坐标轴垂直时，得到的投影为三视图，这是投影方向与这个坐标轴的方向一致；否则，得到的投影为正轴侧图2、三视图包括主、侧、俯视图三种，投影面分别于x/y/z轴垂直3、优点：反映形体的实际尺寸，工程制图中常用三视图来测量形体间的距离、角度以及相互位置关系。

4、缺点：三视图上只有物体一个面的投影，只有将三个图放在一起，才能综合物体的空间形状二、三视图的计算1>确定三维物体上个点的位置坐标2>引入齐次坐标，求出所做变换相应的变换矩阵3>将所做变换用矩阵表示，通过运算求得三维物体上各点经变换后的点坐标值4>由变换后得到的二维点绘出三维物体投影后的三视图三、1>主视图：将三维物体xoz面（又称v面）做垂直投影，得到主视图2>俯视图：将三维物体xoy面（又称h面）做垂直投影，得到俯视图为了让其与主视图在一个平面内，让俯视图绕x轴旋转90°。

计算机形学三维几何变换计算机形学是计算机科学中的一个重要分支，主要研究计算机图形学中的各类图形的数学描述方法和计算机图形学技术的应用。

其中，三维几何变换是计算机形学中的一项重要内容。

本文将介绍三维几何变换的概念、常见的三维几何变换操作以及其在计算机图形学中的应用。

一、概述三维几何变换是指对三维空间中的图形进行平移、旋转、缩放等操作，从而改变图形的位置和形状的过程。

三维几何变换是计算机图形学中非常常用的操作，可以实现物体的移动、旋转、缩放等效果。

二、三维几何变换的操作1. 平移（Translation）平移是指将图形沿指定的轴方向移动一定距离。

平移操作可以简单地理解为将图形的每一个顶点坐标向指定方向移动相同距离。

平移操作的数学表达式为：\[T(x,y,z) = (x + dx, y + dy, z + dz)\]其中，(x,y,z)表示原始顶点坐标，(dx,dy,dz)表示沿(x,y,z)轴平移的距离。

2. 旋转（Rotation）旋转是指将图形绕指定轴进行旋转。

旋转操作可以用欧拉角、四元数、矩阵等多种方式进行计算。

旋转操作的数学表达式为：\[R(x,y,z) = M(x,y,z)\]其中，(x,y,z)表示旋转前的坐标，M表示旋转变换矩阵。

旋转变换矩阵的计算方式有很多，最常见的是使用旋转角度和旋转轴来计算旋转矩阵。

3. 缩放（Scaling）缩放是指将图形沿各个轴向相应的方向按比例进行扩大或缩小。

缩放操作可以用不同的比例因子对每个顶点坐标进行缩放计算。

缩放操作的数学表达式为：\[S(x,y,z) = (sx, sy, sz)(x,y,z)\]其中，(x,y,z)表示原始顶点坐标，(sx,sy,sz)表示在x轴、y轴和z轴方向的缩放比例。

4. 其他变换操作除了平移、旋转和缩放之外，三维几何变换还可以包括倾斜、翻转、剪切等其他操作。

这些操作都是通过对图形的顶点坐标进行适当的数学计算而实现。

三、三维几何变换的应用三维几何变换在计算机图形学中有广泛的应用。

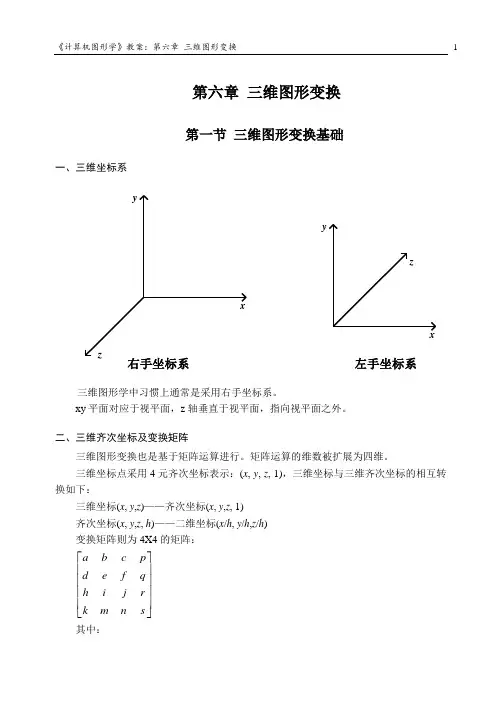
第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。

xy 平面对应于视平面，z 轴垂直于视平面，指向视平面之外。

二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。

矩阵运算的维数被扩展为四维。

三维坐标点采用4元齐次坐标表示：(x , y , z , 1)，三维坐标与三维齐次坐标的相互转换如下：三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中：平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种，即绕三个坐标轴的旋转变换。

(1)绕z 轴旋转γ角旋转后z 值不变，x,y 值将发生改变，x,y 值的计算公式与平面旋转相同，即：zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有：)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变，y 和z 的坐标值将改变，相当于在yz 平面上绕平面原点进行旋转变换。

平面转转变换的公式为：ααααcos sin sin cos y x y y x x +='-='对应而来，这里y 对应于x ，z 对应y ，有：ααααcos sin sin cos z y z z y y +='-='则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时，z 对应于x ，x 对应于y 。

计算机图形学中的三维变换与投影算法计算机图形学是研究计算机中图形的表示、生成、处理和显示的学科。

在计算机图形学中，三维变换和投影算法是非常重要的技术，它们可以用来对三维物体进行位置、姿态和尺寸的调整，并将其投影到二维画面上。

三维变换是指通过对三维物体的顶点进行一系列变换操作，来改变物体的位置、形状和方向。

常用的三维变换操作包括平移、旋转和缩放。

平移操作改变物体的位置，旋转操作改变物体的方向，而缩放操作改变物体的尺寸。

通过组合不同的变换操作，可以实现复杂的三维物体的变换。

平移是通过将物体的每个顶点按照指定的距离移动来改变物体的位置。

旋转是通过将物体的每个顶点绕着旋转中心按照指定的角度旋转来改变物体的方向。

缩放是通过将物体的每个顶点按照指定的比例因子进行缩放来改变物体的尺寸。

这些变换操作可以通过矩阵运算来进行计算，从而实现对三维物体的变换。

投影是将三维物体投影到二维画面上的操作。

在计算机图形学中，常用的投影算法有平行投影和透视投影。

平行投影是将物体的每个顶点沿着平行于视线的方向进行投影，得到二维画面上的对应点。

透视投影则考虑到物体离视点的距离，并根据投影面和视点的位置关系而调整投影结果。

通过投影操作，可以将三维物体在计算机屏幕上展示出来，从而实现真实感的图形显示。

在实际应用中，三维变换和投影算法被广泛应用于计算机游戏、虚拟现实、计算机辅助设计等领域。

通过三维变换，可以实现物体的动画效果，使得游戏或虚拟现实场景更加逼真。

而通过投影算法，可以实现对物体的观察和测量，帮助设计师更好地进行产品设计和展示。

总结来说，计算机图形学中的三维变换和投影算法是实现三维物体在计算机中显示和操作的关键技术。

通过对物体进行平移、旋转和缩放等变换操作，可以改变物体的位置、方向和尺寸；而通过投影操作，可以将三维物体投影到二维画面上展示出来。

这些技术在计算机游戏、虚拟现实和计算机辅助设计等领域发挥着重要的作用，推动了计算机图形学的发展。