第5章之一三维图形生成和变换技术-1(计算机图形学)资料

第五章图形变换重 点：掌握二维几何变换、二维观察变换、三维几何变换以及三维观察变换。

难 点：理解常用的平移、比例、旋转变换，特别是复合变换。

课时安排：授课4学时。

图形变换包括二维几何变换， 二维观察变换，三维几何变换和三维观察变换。

为了能使各种几何变换（平移、旋转、比例等）以相同的矩阵形式表示，从而统一使用矩阵乘法运算来实现变 换的组合，现都采用齐次坐标系来表示各种变换。

有齐次坐标系齐次坐标系：n 维空间中的物体可用 n+1维齐次坐标空间来表示。

例如二维空间直线 ax+by+c=O ，在齐次空间成为 aX+bY+cW=0 ，以X 、Y 和W 为三维变量，构成没有常数项的 三维平面（因此得名齐次空间）。

点P （x 、y ）在齐次坐标系中用P （wx,wy,w ）表示，其中 W 是不为零的比例系数。

所以从 n 维的通常空间到 n+1维的齐次空间变换是一到多的变换，而其反变换 是多到一的变换。

例如齐次空间点P （X 、Y 、W ）对应的笛卡尔坐标是 x=X/W 和y=Y/W 。

将通一地用矩阵乘法来实现变换的组合。

常笛卡尔坐标用齐次坐标表示时， W 的值取1。

采用齐次坐标系可以将平移、比例、旋转这三种基本变换都以相同的矩阵形式来表示,并统齐次坐标系在三维透视变换中有更重要的作用, 示形它使非线形变换也能采用线形变换的矩阵表式。

图形变换平移变换图示如图所示，它使图形移动位置。

新图 p'的每一图元点是原图形 p 中每个图元点在向分别移动Tx 和Ty 产生，所以对应点之间的坐标值满足关系式x'=x+Tx y'=y+Ty可利用矩阵形式表示成：[x' y' ] = : x y ] + : Tx Ty ]简记为：P'= P+T , T= : Tx Ty ］是平移变换矩阵（行向量）二堆几何变换1 1二维观察变換三维几诃变换平移变换 比例变换 陡转变换 对称变换 错切变换 仿肘变换 复合变换平移变换 比例变换 旋转变换 绕空间任意轴離转 对称变换 蜡切变换三维观察变5.1二维几何变换二维几何变换就是在平面上对二维点的坐标进行变换，从而形成新的坐标。

195 5.3.3 三维图形透视投影变换透视投影属于中心投影，透视图也是一种将三维物体用二维平面来表达的立体图。

与轴测图不同，它是用中心投影法，通过空间一点（即投影中心）将立体投射到投影面上所得到的投影图，如图5.37所示。

投影中心又称为视点，它相当于观察者的眼睛。

投影面置于视点与立体之间，将立体上各点与视点相连所得到的投影线分别与投影面相交，其交点就是立体上相应点的透视投影，再将其依次相连，即获得具有真实立体感的透视图。

透视投影可用矩阵变换方法获得，在4 × 4阶变换矩阵中第4列元素p 、q 、r 、s 称为透视参数，若赋其非零数值即形成透视变换矩阵。

T =a b c p d e f q g h i r l m n s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1．点的透视变换如图5.38所示，在y 轴上取一点E 为视点，投影面取xOz 面（V 面），E 点到V 面的距离记为d ，对于空间里任一点，D (x ，y ，z ) 与视点E 的连线DE 与V 面的交点为D '(x '，y '，z ')，即为D 的透视投影，同样A 的透视投影为A '，B 的透视投影为B '，C 的透视投影为C '。

根据图5.38可以找到空间点坐标与点的透视投影坐标的关系。

图5.37 透视投影 图5.38 透视投影坐标关系 因为△BCE 与△B 'C 'E 相似，所以，'x d x y d =−+，即'1x x y d=−。

同理可得：'z d z y d =−+，即'1z z y d=− 设1q d =−，则1x x qy ′=+，1z z qy′=+。

计算机形学三维几何变换计算机形学是计算机科学中的一个重要分支，主要研究计算机图形学中的各类图形的数学描述方法和计算机图形学技术的应用。

其中，三维几何变换是计算机形学中的一项重要内容。

本文将介绍三维几何变换的概念、常见的三维几何变换操作以及其在计算机图形学中的应用。

一、概述三维几何变换是指对三维空间中的图形进行平移、旋转、缩放等操作，从而改变图形的位置和形状的过程。

三维几何变换是计算机图形学中非常常用的操作，可以实现物体的移动、旋转、缩放等效果。

二、三维几何变换的操作1. 平移（Translation）平移是指将图形沿指定的轴方向移动一定距离。

平移操作可以简单地理解为将图形的每一个顶点坐标向指定方向移动相同距离。

平移操作的数学表达式为：\[T(x,y,z) = (x + dx, y + dy, z + dz)\]其中，(x,y,z)表示原始顶点坐标，(dx,dy,dz)表示沿(x,y,z)轴平移的距离。

2. 旋转（Rotation）旋转是指将图形绕指定轴进行旋转。

旋转操作可以用欧拉角、四元数、矩阵等多种方式进行计算。

旋转操作的数学表达式为：\[R(x,y,z) = M(x,y,z)\]其中，(x,y,z)表示旋转前的坐标，M表示旋转变换矩阵。

旋转变换矩阵的计算方式有很多，最常见的是使用旋转角度和旋转轴来计算旋转矩阵。

3. 缩放（Scaling）缩放是指将图形沿各个轴向相应的方向按比例进行扩大或缩小。

缩放操作可以用不同的比例因子对每个顶点坐标进行缩放计算。

缩放操作的数学表达式为：\[S(x,y,z) = (sx, sy, sz)(x,y,z)\]其中，(x,y,z)表示原始顶点坐标，(sx,sy,sz)表示在x轴、y轴和z轴方向的缩放比例。

4. 其他变换操作除了平移、旋转和缩放之外，三维几何变换还可以包括倾斜、翻转、剪切等其他操作。

这些操作都是通过对图形的顶点坐标进行适当的数学计算而实现。

三、三维几何变换的应用三维几何变换在计算机图形学中有广泛的应用。

《计算机图行学》学习包本课程为有关专业的必修课程（或选修课程）。

通过本课程的教学，学生可以学习、了解和掌握计算机图形学中有关的基本原理、概念、方法和技术，培养和提高交互式图形设计的能力。

计算机图形学与图象处理，计算机图形学的研究内容，计算机图形学的发展简史，计算机图形学的发展方向，本课程教学要求与学习方法。

本章无习题计算机图形系统的组成、功能与分类，计算机图形显示器，图形输入设备，图形输出设备，图形软件系统，图形软件标准。

课后习题1. 某光栅系统中，显示器的分辨率为1280×768，其中每个象素点的颜色深度为12 bit，则该系统需要多大的帧缓存（即多少KB）？2. 有甲乙两台光栅图形显示器，它们的产品说明书介绍均称可以显示4096种颜色，但甲机在显示一幅画面时却只有256种颜色，问其中究竟是什么原因？参考答案1．1280×768×12 / (8×1024) = 1440(KB)2．(1) 甲机：8个位平面，采用一张有256个单元，每个单元有12 bit的彩色查找表。

(2) 乙机：12个位平面，没有采用查找表。

1点的生成，生成直线的DDA算法和Bresenham 算法，二次曲线，区域的简单种子填充算法和扫描线种子填充算法，多边形的扫描转换，字符的生成，反走样技术。

课后习题1. 用对称DDA算法画出A(0,0)到B(5,3)连线的各象素点的位置，并在表内填出相应的中间数据。

rx=5, ry=3,x=0,y=0,steps=5,dx=1,dy=0.6;2. 用Bresenham算法画出A(0,0)到B(5,3)连线的各象素点的位置，并在表内填出相应的中间数据。

dx=5, dy=3, d=2dy-dx=1, x=0, y=0, 2dy-2dx=-4, 3dy=6;23. 用Bresenham算法画出圆心为（0,0），半径为8的顺时针90至45的1/8圆弧上各象素点的位置。

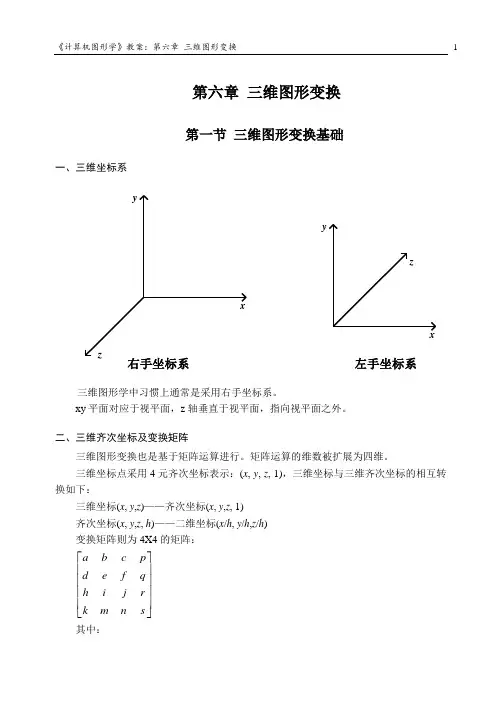
第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。

xy 平面对应于视平面，z 轴垂直于视平面，指向视平面之外。

二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。

矩阵运算的维数被扩展为四维。

三维坐标点采用4元齐次坐标表示：(x , y , z , 1)，三维坐标与三维齐次坐标的相互转换如下：三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中：平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种，即绕三个坐标轴的旋转变换。

(1)绕z 轴旋转γ角旋转后z 值不变，x,y 值将发生改变，x,y 值的计算公式与平面旋转相同，即：zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有：)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变，y 和z 的坐标值将改变，相当于在yz 平面上绕平面原点进行旋转变换。

平面转转变换的公式为：ααααcos sin sin cos y x y y x x +='-='对应而来，这里y 对应于x ，z 对应y ，有：ααααcos sin sin cos z y z z y y +='-='则变换矩阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时，z 对应于x ，x 对应于y 。