汇交力系与力偶系的应用共29页

第二章 平面汇交力系与平面力偶系§2.1平面汇交力系合成与平衡的几何法一、汇交力系合成与平衡的几何法 汇交力系：是指各力的作用线汇交于同一点的力系。

若汇交力系中各力的作用线位于同一平面内时，称为平面汇交力系，否则称为空间汇交力系。

1、平面汇交力系的合成先讨论3个汇交力系的合成。

设汇交力系1F ，2F ，3F汇交于O （图1），由静力学公理3：力的平行四边形法则（力的三角形）可作图2，说明)(),,(321F F F F=如图和图所示，其中321F F F F ++=F2F 3F OFO1F 2F 3F12F讨论：1）图2中的中间过程12F 可不必求，去掉12F 的图称为力多边形，由力多边形求合力大小和方向的方法称为合力多边形法则。

2）力多边形法则：各分力矢依一定次序首尾相接，形成一力矢折线链，合力矢是封闭边，合力矢的方向是从第一个力矢的起点指向最后一个力矢的终点。

3）上述求合力矢的方法可推广到几个汇交力系的情况。

结论：汇交力系合成的结果是一个合力，合力作用线通过汇交点，合力的大小和方向即：∑=i F F用力多边形法则求合力的大小和方向的方法称为合成的几何法。

2．平面汇交力系的平衡1F 2F iF 2-n F 1-n F n F设作用在刚体上的汇交力系),,(21n F F F 为平衡力系，即 0),,(21≡n F F F先将121,,-n F F F 由力多边形法合成为一个力1-N F，（∑-=-=111n i i N F F ）0),(),,(121≡≡-n N n F F F F F由静力公理1，作用在刚体上二力平衡的必要充分条件是：1-N F 与n F等值，反向，共线，即n N F F =-1， 可得01=+-n N F F，或0=∑i F结论：平面汇交力系平衡的必要与充分条件是：力系中各力的乖量和为零，用几何法表示的平衡条件是0=∑i F，力多边形自行封闭。

例1． 已知：简支梁AB ，在中点作用力F，方向如图，求反力FA B C45F AF BACα 45FF BF α解：1。

平面汇交力系和平面力偶系
平面汇交力系和平面力偶系是平面力学中的两个重要概念。

平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。

在平面汇交力系中，力的大小和方向可以通过力的矢量表示。

平面汇交力系的合成可以通过力的多边形法则来进行，即将各个力按照首尾相接的顺序连接起来，形成一个封闭的多边形，合力则为这个多边形的封闭矢量。

平面力偶系是指由若干个力偶组成的力系，其中力偶是由大小相等、方向相反且不共线的两个力组成的力矩对。

在平面力偶系中，力偶的作用效果是产生旋转，而不是平移。

平面力偶系的合成可以通过力偶矩的代数和来进行。

平面汇交力系和平面力偶系在工程和物理学中有广泛的应用。

在结构分析、机械设计和力学问题中，常常需要考虑和分析平面汇交力系和平面力偶系的作用效果。

总的来说，平面汇交力系和平面力偶系是平面力学中的重要概念，它们的合成和平衡条件对于理解和解决平面力学问题至关重要。

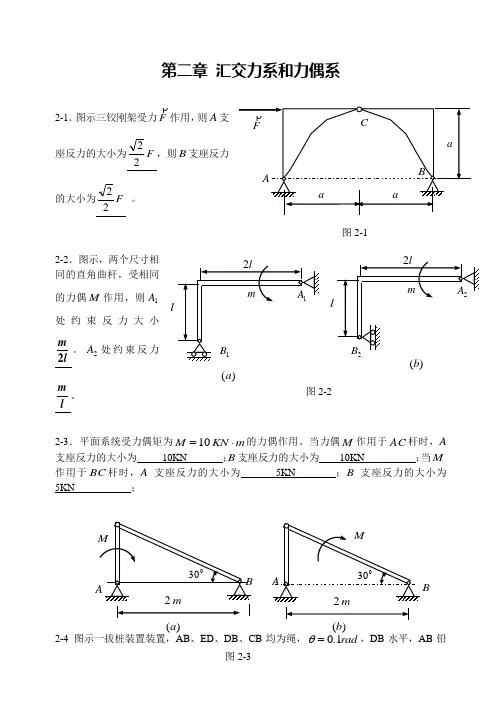
第二章汇交力系和力偶系2-1．图示三铰刚架受力F作用，则A支座反力的大小为F22，则B支座反力的大小为F22。

2-2．图示，两个尺寸相同的直角曲杆，受相同的力偶M作用，则1A处约束反力大小lm2。

2A处约束反力lm。

2-3．平面系统受力偶矩为mKNM⋅=10的力偶作用。

当力偶M作用于AC杆时，A 支座反力的大小为10KN ；B支座反力的大小为10KN ；当M 作用于BC杆时，A支座反力的大小为5KN ；B支座反力的大小为5KN ；2-4 图示一拔桩装置装置，AB、ED、DB、CB均为绳，rad1.0=θ，DB水平，AB铅)(a)(bl l图2-2图2-1)(a垂。

力N F 800=，求绳AB 作用于桩上的力。

解：. 1、 以D 点为研究对象N F F F F N F F F F DB DE DB x DE DE y 80000cos80000sin0==-∑===-=∑θθ2、 以B 点为研究对象NBA F BA F BC F F N BC F BD F BC F F Y X 800000cos 0800000sin 0==-∑===-=∑θθC图2-4BAF BBDF BC F DBF FDDEF2-5 物体重P =20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞D 上，如图所示。

转动绞，物体便能升起。

设滑轮的大小、AB 与CB 杆自重及摩擦略去不计，A ，B ，C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆CB 所受的力。

解：以B 结点为研究对象图2-5030sin 30cos 0030cos 30sin 0=ο-ο--∑==-ο-ο-∑=T F BC F BA F F P T F BC FF x y PBAF BCF TF BN BAF NBC F 64.5464.74=-=2-6 已知梁AB 上作用一力偶M ，梁长为l ，梁重不计，求a,b,c 三种情况下，支座A 和B 处的约束力。

Engineering Mechanics（第3版）普通高等教育“十一五”国家级规划教材高等教育出版社第3 章汇交力系和力偶系3.1 汇交力系的合成3.2 汇交力系的平衡3.3 力偶系小结思考题使这些矢量的模及方向分别和力系中各力的模及方向相同，得力多边形，如图的长度及方向,,,,a a a a a a a a a a a a 5434cos50cos60cos20F F --34sin50sin60sin 20F F +-5428'5kN=30cos30cos300BF +=sin30sin300BF W +-=5kN30=cos30cos300B F +=50.236.860sin30sin300BCF '-=cos30cos300W -=(a)cos60sin50.2sin50.20BD BE F F --=cos50.2sin 36.8cos50.2sin 36.8sin 60sin 200BE BC F F -+=(e)cos50.2cos36.8cos50.2cos36.8sin 60cos 20BE BC F F -+3.3 力偶系3.3.1 力偶力偶矩矢力偶的等效大小相等、方向相反且不共线的一对平行力和所组成的力系，称为力偶，记作（F ，F ´）。

力偶对刚体只产生转动效应。

例如司机转动方向盘、钳工转动丝锥加工螺纹的操作等都是力偶对物体的作用，如图3-7所示。

F ′FM图3—7F ′F设有一对力F 、F ´分别作用于物体的A ，B 两点，构成一力偶。

力偶所在的平面称为力偶作用面，两力之间的垂直距离d 称为力偶臂，如图3-8a 所示。

图3—8(a)FF'r Ar B M dO AB 力偶作用面r (b)M力偶矩矢作为矢量，应由以下三个因素决定：（1）力偶矩矢M 的大小（以力偶矩M 表示），即力偶中任一力的大小与力偶臂的乘积，有（3-9）（2）力偶矩矢的方位，应垂直于力偶作用面（图3-8a ）。

第二章平面汇交力系与平面力偶系一、要求1、掌握平面汇交力系合成（分解）的几何法。

能应用平衡的几何条件求解平面汇交力系的平衡问题。

2、能正确地将力沿坐标轴分解和求力在坐标轴上的投影。

对合力投影定理应有清晰的理解。

3、能熟练地运用平衡方程求解平面汇交力系的平衡问题。

4、对于力对点的矩应有清晰的理解，并能熟练地计算。

5、深入理解力偶和力偶矩的概念。

明确平面力偶的性质和平面力偶的等效条件。

6、掌握平面力偶系的合成方法，能应用平衡条件求解力偶系的平衡问题。

二、重点、难点1、 力在坐标轴上的投影，合力投影定理，平面汇交力系的平衡条件及求解平衡问题的解析法。

2、 力对点之矩的计算，力偶矩的概念，平面力偶性质和力偶等效条件。

三、学习指导平面汇交力系合成的结果是一个合力，合力作用线通过力系的汇交点，合力的大小和方向等于力系的矢量和，即∑==+⋅⋅⋅⋅⋅⋅++=ni i n F F F F R 121或简化为∑=F R上式是平面矢量方程，只可以求解两个未知数。

每一个力都有大小和方向两个要素（因为力的汇交点是已知的），因此，方程中只能有两个要素是未知的。

矢量方程的解法有：几何法和解析法。

只有力沿直角坐标轴分解的平行四边形才是矩形。

力在轴上投影的大小等于分力的大小，投影的正负表示分力沿坐标轴的方向。

平面汇交力系平衡的必要和充分条件是力系的合力为零。

即∑R=F这个平面的矢量方程可解两个未知数，解法有几何法和解析法。

（1）平衡的几何条件：平面汇交力系的力多边形封闭。

（2）平衡的解析条件：平面汇交力系的各分力在两个坐标轴上投影的代数和分别等于零即：∑=0YX；∑=0对于平衡方程，和平面汇交力系合成与分解的解析法一样，一般也选直角坐标系。

但在特殊情况下，有时选两个相交的相互不垂直的坐标轴，可使问题的求解简化。

这是因为平衡时合力恒等于零，合力在任一坐标轴的投影也恒等于零，所以，不一定局限在直角坐标系。

合力投影定理与合力矩定理是结构静力计算经常要用到的两个定理。