下载文档原格式
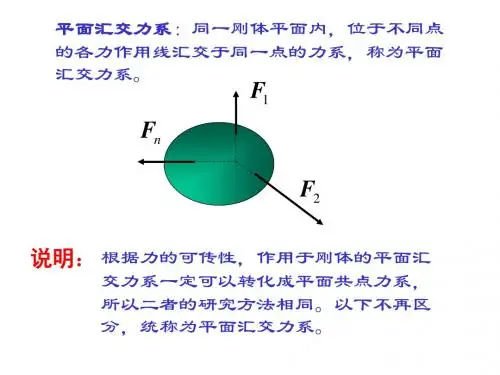
第二章 平面汇交力系与平面力偶系§2.1平面汇交力系合成与平衡的几何法一、汇交力系合成与平衡的几何法 汇交力系：是指各力的作用线汇交于同一点的力系。
若汇交力系中各力的作用线位于同一平面内时，称为平面汇交力系，否则称为空间汇交力系。
1、平面汇交力系的合成先讨论3个汇交力系的合成。
设汇交力系1F ，2F ，3F汇交于O （图1），由静力学公理3：力的平行四边形法则（力的三角形）可作图2，说明)(),,(321F F F F=如图和图所示，其中321F F F F ++=F2F 3F OFO1F 2F 3F12F讨论：1）图2中的中间过程12F 可不必求，去掉12F 的图称为力多边形，由力多边形求合力大小和方向的方法称为合力多边形法则。
2）力多边形法则：各分力矢依一定次序首尾相接，形成一力矢折线链，合力矢是封闭边，合力矢的方向是从第一个力矢的起点指向最后一个力矢的终点。
3）上述求合力矢的方法可推广到几个汇交力系的情况。
结论：汇交力系合成的结果是一个合力，合力作用线通过汇交点，合力的大小和方向即：∑=i F F用力多边形法则求合力的大小和方向的方法称为合成的几何法。
2．平面汇交力系的平衡1F 2F iF 2-n F 1-n F n F设作用在刚体上的汇交力系),,(21n F F F 为平衡力系，即 0),,(21≡n F F F先将121,,-n F F F 由力多边形法合成为一个力1-N F，（∑-=-=111n i i N F F ）0),(),,(121≡≡-n N n F F F F F由静力公理1，作用在刚体上二力平衡的必要充分条件是：1-N F 与n F等值，反向，共线，即n N F F =-1， 可得01=+-n N F F，或0=∑i F结论：平面汇交力系平衡的必要与充分条件是：力系中各力的乖量和为零，用几何法表示的平衡条件是0=∑i F，力多边形自行封闭。
例1． 已知：简支梁AB ，在中点作用力F，方向如图，求反力FA B C45F AF BACα 45FF BF α解：1。
平面汇交力系和平面力偶系
平面汇交力系和平面力偶系是平面力学中的两个重要概念。
平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。
在平面汇交力系中，力的大小和方向可以通过力的矢量表示。
平面汇交力系的合成可以通过力的多边形法则来进行，即将各个力按照首尾相接的顺序连接起来，形成一个封闭的多边形，合力则为这个多边形的封闭矢量。
平面力偶系是指由若干个力偶组成的力系，其中力偶是由大小相等、方向相反且不共线的两个力组成的力矩对。
在平面力偶系中，力偶的作用效果是产生旋转，而不是平移。
平面力偶系的合成可以通过力偶矩的代数和来进行。
平面汇交力系和平面力偶系在工程和物理学中有广泛的应用。
在结构分析、机械设计和力学问题中，常常需要考虑和分析平面汇交力系和平面力偶系的作用效果。
总的来说，平面汇交力系和平面力偶系是平面力学中的重要概念，它们的合成和平衡条件对于理解和解决平面力学问题至关重要。
第二章 平面汇交力系与平面力偶系平面汇交力系与平面力偶系是两种简单力系，是研究复杂力系的基础，本章将分别研究两种力系的合成与平衡问题。
§2-1平面汇交力系合成与平衡的几何法平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。
一、平面汇交力系合成的几何法、力多边形法则如图a 所示，作用在刚体上的四个力1F ，2F ，3F 和4F 汇交于点A 。
连续应用平行四边形法则，即可求出通过汇交点A 的合力R 。
合力R 的大小和方向也可用图(b)所示的力三角形法则或力多边形法则得到。
后者，作出图示首尾相接的开口的力多边形abcde ,封闭边矢量ae 即所求的合力。
通过力多边形求合力的方法称为几何法。
改变分力的作图顺序，力多边形改变，如图(c)所示，但其合力不变。
平面汇交力系可合成为通过汇交点的合力，其大小和方向等于各分力的矢量和。
即∑==+++=n i i 1n 21F F F F R 简写为 ∑=F R （2-1）二、平面汇交力系平衡的几何条件平面汇交力系平衡的必要和充分条件是：力系的合力等于零。
其矢量表达式为∑==0F R （2-2）力系平衡的几何条件是：力系的力多边形自行封闭。
例2-1 如图所示，钢梁的重量kN 6N 1063=⨯=P ,︒=30θ，试求平衡时钢丝绳的约束力。
解：取钢梁为研究对象。
作用力有：钢梁重力P ，钢绳约束力AF 和B F 。
三力汇交于D 点 ，受力如图a 所示。
作力多边形，求未知量。
首先选择力比例尺，以1cm 长度代表2kN 。
其次，任选一点e ，作矢量ef ，平行且等于重力P ，再从e 和f 两点分别作两条直线，与图(a)中的A F 、B F 平行，相交于h 点，得到封闭的力三角形efh 。
按各力首尾相接的次序，标出fh 和he 的指向，则矢量和he 分别代表力A F 和B F （如图b 所示）。
按比例尺量得和的长度为：45.3=fh cm ， 45.3=he cm即 45.3145.3=⨯=A F kN ，45.3145.3=⨯=B F kN 从力三角形可以看到，在重力P 不变的情况下，刚绳约束力随角θ增加而加大。
平面汇交力系与平面力偶系
作业参考答案与解答
1．四力作用于一点，其方向如图所示。
已知各力的大小为：F 1=50N ，F 2=80N ，F 3=60N ，F 4=100N 。
求力系的合力。
答案: 0
),( N 02.52R R
≈∠=i F F
2．一均质球重P =1000N ，放在两个相交的光滑斜面之间如图示。
如斜面AB 的倾角ϕ =45º，而斜面BC 的倾角θ =60º。
求两斜面的约束力F D 和F E 的大小。
解：受力图如上右图所示，为避免解联立方程，取轴x 、y 分别与F D 、F E 垂直。
由 ∑=0x F ， 015cos 45sin =+−o
o E
F P 解得
N 73215
cos 45sin ==o
o P F E 由 ∑=0y
F
， 015cos 60sin =+−o o D F P
解得
N 89615
cos 60sin ==o
o
P F D
3．均质杆AB 长l ，置于销子C 与铅垂面间，如图所示。
不计摩擦力，求平衡时杆与铅垂线间的夹角θ 。
解：由三力平衡汇交定理，杆AB 所受主动力和约束力的作用线汇交于点O ，如右上图所示。
根据几何关系有
θθθ32sin sin sin 2a
AC AO l AD =
=== 解得： 3
2arcsin l
a =θ
4．三个相同的光滑圆柱放置如图示，求圆柱不至于倒塌时θ 角的最小值。
解：本题关键在于要清楚当θ 角取平衡时的最小值时，系统处于临界平衡状态，圆柱O 2与圆柱O 3之间的相互作用力为零。
考虑临界状态，先取圆柱O 1为研究对象，受力图见图（b ）。
由 31213121 , 030sin 30sin , 0F F F F F
x
=⇒=−=∑o o
由
P F F P F F F y 33 , 030cos 30cos , 031213121==⇒=−+=∑o o 再取圆柱O 3为研究对象，受力图见图（c ）。
由
P F F P F F 3
3 , 0sin )30sin( , 0133113=
==−−=∑注意θθξo 解上式得 3
31tan =
θ， 即 3
31tan min =
θ
5．杆AB 以铰链A 及弯杆BC 支持，杆AB 上作用一力偶，其力偶矩大小为M ，顺时针转向，如图所示。
所有杆件的重量不计，求铰链A 与C 的约束力。
解：注意到构件BC 为二力构件，故B 处约束力的作用线为铅垂。
以杆AB 为研究对象，则A 处约束力的作用线也是铅垂，且与B 处约束力构成一力偶。
解题过程略。
答案： .。
, 方向铅垂a
M
F F C A ==
6．图示机构中杆AB 上有一导槽，套在CD 杆的销子E 上，在AB 和CD 杆上各有一力偶作用，如图所示。
己知M 1=1000N ·m ，不计杆重及摩擦。
求机构在图示位置平衡时力偶矩M 2的大小。
解：先取杆AB 为研究对象，求出AB 与CD 之间的作用力，再以CD 为研究对象即可求得结果，过程略。
答案： m N 10002⋅=M
[选做题]：分析下列结构中每个构件及整体的受力情况，求中间铰E 、B 及支座A 、C 的约束力。
图中没有画上重力矢的构件都不考虑自重。
解：先取轮E 为研究对象，受力图如下左图 由
045cos , 0=−=∑P F F
E y
o
解得 P F E 2=
再取杆DBE 为研究对象，受力图如下中图
将所有力沿E
F ′方向投影解得 P F F F E E
B 222==′= 最后取杆DBE 、杆AB
C 和杆C
D 的组合为研究对象，受力图如下右图
由 045cos , 0=−=∑o E A x
F F F 由
045cos , 0=−=∑o E C y
F F F
解得 P F F C A ==。
