3.8-晶格热容的量子理论
- 格式:ppt
- 大小:1.21 MB
- 文档页数:36



固体物理教学⼤纲课程名称固体物理课程性质专业必修课《固体物理》教学⼤纲⼀、课程名称:固体物理⼆、课程性质:专业必修课三、课程教学⽬的:(⼀)课程⽬标:通过固体物理学课程的学习,使学⽣树⽴起晶体内原⼦、电⼦等微观粒⼦运动的物理图像及其有关模型,掌握晶体内微观粒⼦的运动规律及其与晶体宏观性能的物理联系,深刻理解晶体宏观性能的微观物理本质,为进⼀步学习和研究固体物理学各种专门问题及相关领域的内容建⽴初步的理论基础。
(⼆)教学⽬标:第⼀章晶体结构【教学⽬标】通过本章的教学,使学⽣了解晶格结构的实例、⾮晶态和准晶态的特征;理解和掌握晶体结构的周期性特征及其描述⽅法;理解和掌握晶体结构的对称性特征及其描述⽅法;理解和掌握倒格⼦的定义及其与正格⼦的关系;熟悉有关晶体结构的基本分析与计算。
借助于多媒体展⽰,使学⽣建⽴起晶体结构特征的直观图像。
第⼆章晶体的结合【教学⽬标】通过本章的教学,使学⽣了解晶体结合⼒的⼀般性质;掌握晶体的结合类型与特征;理解元素和化合物晶体结合的规律性;掌握离⼦晶体的结合能、体积弹性模量的计算;掌握范德⽡⽿斯晶体的结合能、体积弹性模量的计算。
在教学中,能够使学⽣认识到吸引与排斥的⽭盾的差别和对⽴统⼀是认识与理解固体的结合规律与性质的关键,培养学⽣的辩证思维能⼒。
第三章晶格振动与晶体的热学性质【教学⽬标】通过本章的教学,能够使学⽣理解简谐近似、格波概念、声⼦概念;理解玻恩-卡曼边界条件;了解三维格波的⼀般规律、晶格振动的⾮简谐效应;了解确定晶格振动谱的实验⽅法;掌握⼀维单原⼦、双原⼦晶格振动的格波解与⾊散关系;掌握晶格振动模式密度的计算⽅法;理解晶格热容量的量⼦理论、掌握爱因斯坦模型与德拜模型;理解格林爱森近似、掌握晶格状态⽅程。
结合例题分析和习题训练,提⾼学⽣分析问题和解决问题的能⼒。
第四章能带理论【教学⽬标】通过本章的教学,使学⽣能够了解晶体能带理论的基本假设和处理问题的基本思路;理解布洛赫定理及其推论的证明,掌握晶体能带的基本特征;熟悉克龙尼克—潘纳模型的求解与结论;熟悉布⾥渊区、费⽶⾯等基本概念;了解平⾯波⽅法、赝势⽅法;掌握近⾃由电⼦近似⽅法及其结论;掌握紧束缚近似⽅法的运⽤;掌握能态密度的计算⽅法。

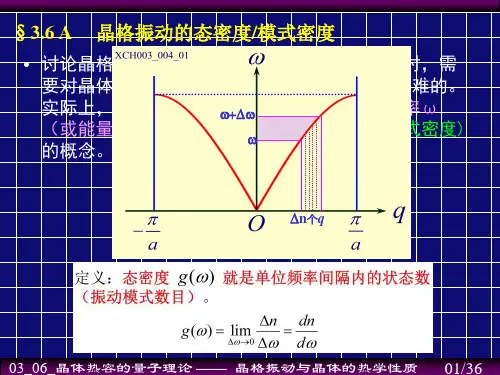
第25讲、晶格振动的量子理论(授课时间2课时)本讲要点• 晶格振动是一种集体振动——称为格波* 格波可以不是简谐的,如是非谐的,可以展开为简谐振动的迭加;在简谐近似下,格波就是简谐波,这时格波之间的没有相互作用• 独立的简谐振动模式——声子——简谐振动的能量量子格波能量→能量量子化→声子主要内容1. 一维单原子链解的讨论2. 简正坐标:一维情况3. 简正坐标:三维情况4. 晶格振动的量子化1、一维单原子链解的讨论• 方程• 解• 设问:那么,这个解到底表示什么?• 位移与频率ω(q)有关* 如果位相差2\pi的整数倍时,位移完全相等• 而振动频率与n无关!* 这表示所有的原子都同时在做的频率为ω的振动讨论:位移?• 位移与格点* 不同格点原子的位移,由Bloch定理决定,差一个相因子* 这说明,各个原子的振动并不是独立的• 晶格振动是一种集体的振动!* 对应某个给定频率,需要N个互相有关联的位移来描写在不同原胞中原子具有这个频率的集体振动,这说明振动是互相有关的* 或者说,提到某个频率的振动,就得与这N个的位移联系起来• 位移与波矢* 波矢的取值由周期性边界条件决定* 这是振动的状态数目,一个状态q对应s个频率,s即自由度,一维单原子,s=1 • 这些振动互相之间独立,没有关系* 简谐振动• 设问:那么多解,那么,原子到底怎么振动?* 或问:原子在任意时刻t,到底处在什么位置?• 上面只是一个个特解,一般解应是它们的迭加,即在任意时刻t,n格点的原子处在• 振幅与q有关,Aq(t)把e-iωt也包括进去* 即各种不同波矢、不同频率的格波的迭加• 因此用这种方法来确定晶体中各个原子的空间坐标随时间的变化从而描写晶格振动非常复杂* 因为各个原子相互之间是关联的• 问题在哪里?不同原子的振动是互相关联的,* 振动状态是独立的,但每个位移并不是独立的• 自然要问:有无更简便的方法来描写这种振动2、简正坐标:一维情况• 一维单原子链解的分析* 换个角度,如果晶格振动中各个不同的波矢、不同频率的格波的振幅知道了,振动情况也就完全确定了——格波之间没有相互作用* 因此,就没有必要去知道每个原子的空间坐标• 但是原子之间关联怎么办?关联?看势能• 如果能简化交叉项,就可以分离变量。


晶格振动与晶体的热容量关系的理论分析方法的改进在研究晶体的性质和行为时,深入了解晶格振动与晶体的热容量关系是至关重要的。
晶格振动作为晶体中原子的周期性振动,对晶体的热容量有着直接的影响。
本文旨在探讨现有的理论分析方法,并提出改进的方法以更准确地描述晶格振动对热容量的影响。
首先,我们来回顾一下晶体的热容量的定义。
热容量是指单位质量或摩尔的物质在温度变化下吸收或释放的热量。
在晶体中,热容量与晶格振动的频率和振幅有关。
因此,准确地描述晶格振动对热容量的影响是十分重要的。
传统的理论分析方法通常基于经典力学理论和统计物理学原理。
其中一个常用的方法是简谐近似,即将晶体中的原子振动视为简谐振动。
根据这一假设,晶格振动可以通过谐振子模型来描述,其能量与振幅成正比。
然后,利用统计物理学中的玻尔兹曼分布,我们可以计算不同振动模式的平均能量。
最后,将这些能量值代入到求解热容量的公式中,得到晶体的热容量。
然而,简谐近似存在一些局限性。
首先,它假设原子围绕它们的平衡位置振动,而忽略了非平衡位置的振动。
这在高温下会导致计算结果的偏差。
其次,此方法无法很好地处理晶格弛豫效应,即晶体中原子的位置在时间上的变化。
因此,简谐近似的方法无法准确地预测热容量的温度依赖性。
为了改进这些不足,现代的理论分析方法采用了更为复杂的模型和计算技术。
其中之一是分子动力学模拟方法。
分子动力学模拟基于牛顿力学原理,并利用离散的原子模型来模拟晶体中原子的运动。
通过数值计算原子的位置和速度,我们可以模拟晶体在不同温度下的行为,并计算其热容量。
与简谐近似相比,分子动力学模拟方法考虑了晶体中原子的非简谐振动和位置的弛豫效应。
因此,它可以更准确地描述晶格振动对热容量的影响,并获得温度依赖性。
此外,分子动力学模拟方法还可以考虑不同晶体结构、晶体缺陷和外部应力等因素对热容量的影响,具有更广泛的适用性。
除了分子动力学模拟方法,还有其他一些改进的理论分析方法。
例如,基于自洽格林函数理论的方法可以考虑到晶体中电子和声子之间的相互作用,提供了更为准确的热容量计算结果。




§3-5 晶格比热容的量子理论研究固体的比热容是探索固体微观结构与运动机理和重要手段。
固体物理学中的比热容一般是指定容比热容,即()()V VE T C T T ⎛⎫∂= ⎪∂⎝⎭…………………………………………………………(3-5-1)其中()E T 为固体在温度T 时的热力学平均能量。
()V C T 主要是由两部分组成,即()()()V Vc Ve C T C T C T =+………………………………………………………(3-5-2)其中()Vc C T 是晶格(离子)热运动的结果,称晶格比热容;()Ve C T 是电子热运动的结果,称为电子比热容。
电子比热容仅在低温下才起作用。
本节仅涉及晶格比热容。
3. 5. 1 经典理论的困难如果不考虑量子效应,用经典的能量均分定理求N 个原子三维运动的总能量E 。
设晶体有N 个原子,则自由度数为3N ,根据经典统计的能量均分定理,每个简谐振动的平均能量为j B E k T =,因而晶体的总能量为3B E Nk T =,比热容为() 3V B C T Nk =,摩尔比热容为V 0B C (T) =3N k =3R (大约为-125J K mol ⋅⋅),是一个与材料性质和温度无关的常数,此即为杜隆—珀替定律。
该定律在高温下成立,但在低温下不成立。
经实验发现,温度很低时,V C 很快下降,并当T →0时,3V C T ∝,很快趋势于零,如图3-5-13. 5. 2 晶格比热的一般公式我们知道,晶体中原子的热振动可归结为3N 个相互独立的简谐振动模。
每个谐振子的能量均是量子化的。
由于量子化,使得每个振动平均热运动能量不再是B k T ,如果忽略零点能,而成为()() j j n ω q q ,则由式(3-3-14)可得:()B ()1j j j k T E T eωω=- ……………………………………………………………(3-5-3)晶体的总的能量为:()B 3()11j Nj k T j E T eωω==-∑…………………………………………………………(3-5-4)晶体的总热容:()()()()3311N N j j V V Vj j VdE T E T C T C T C T dT ==⎛⎫∂=== ⎪∂⎝⎭∑∑或……………………(3-5-5) 但在具体计算过程中碰到了求和的困难,计算出成果N 个简正振动频率往往是十分复杂的。
3.3 固体热容的量子理论一. 经典理论的困难二. 爱因斯坦模型(Einstein 1907年)三. 德拜模型(Debye 1912年)四. 实际晶体的热容参考:黄昆书 3.8节(p122-132)Kittel 书5.1节(79-87)前面提到:热容是固体原子热运动在宏观性质上的最直接体现,因而对固体原子热运动的认识实际上首先是从固体热容研究开始的,并得出了原子热运动能量是量子化的这个无可争辩的结论。
我们讨论固体热容仍是以揭示原子热运动特征为目的,而完整地介绍热容统计理论应是统计物理的内容。
固体热容由两部分组成:一部分来自晶格振动的贡献,称为晶格热容;另一部分来自电子运动的贡献,称为电子热容。
除非在极低温度下,电子热容是很小的(常温下只有晶格热容的1%)。
这里我们只讨论晶格热容。
典型金属元素定压比热随温度的变化的测量值同Dulong and Petit 定律的比较。
这里Cp =Cv尽管模型仍有不足之处,但Einstein使用一个可调参数T E(ωE)就可以基本解释热容-温度关系的做法应当看作是理论物理工作的一个典范之作。
这充分说明,能量量子化才是理解晶格振动问题的关键,这也间接印证了提出用声子概念讨论晶体性质的必要性。
金刚石比热测量值与Einstein 模型给出结果的比较。
1320KE T三.Debye 模型:Einstein把固体中各个原子的振动看作相互独立的,因而3N个振动频率都相同。
而实际原子之间有很强的相互作用,振动格波的频率不是固定的,而是有一个分布。
Debye(1912)修正了原子是独立谐振子的概念,而考虑晶格的集体振动模式,他假设晶体是连续弹性介质,原子的热运动以弹性波的形式发生,每一个弹性波振动模式等价于一个谐振子,能量是量子化的,并规定了一个弹性波频率上限,称之为德拜频率。
DDebye的比较(实验点是金属镱比热测量值)该图的画法值得注意,取不同物质的区别,突出反映德拜规律TT 见阎守胜:固体物理基础p112 图KCl 的晶格比热在低温低温与T3成正比关系注意:对热容的贡献不仅来自晶格,还有自由电子等。