第4章点的运动和刚体基本运动习题解答080814
- 格式:doc
- 大小:564.50 KB
- 文档页数:12


第四章 刚体的转动一、简答题:1、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案:刚体定轴转动时,若所受合外力矩为零或不受外力矩,则刚体的角动量保持不变。
2、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案:刚体绕定轴转动的转动定律:刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比。
表达式为:αJ M =。
3、写出刚体转动惯量的公式,并说明它由哪些因素确定?答案:dm r J V⎰=2①刚体的质量及其分布;②转轴的位置;③刚体的形状。
二、选择题1、在定轴转动中,如果合外力矩的方向与角速度的方向一致,则以下说法正确的是 ( A )A.合力矩增大时,物体角速度一定增大;B.合力矩减小时,物体角速度一定减小;C.合力矩减小时,物体角加速度不一定变小;D.合力矩增大时,物体角加速度不一定增大2、关于刚体对轴的转动惯量,下列说法中正确的是 ( C ) A.只取决于刚体的质量,与质量的空间分布和轴的位置无关; B.取决于刚体的质量和质量的空间分布,与轴的位置无关; C.取决于刚体的质量,质量的空间分布和轴的位置;D.只取决于转轴的位置,与刚体的质量和质量的空间分布无关;3、有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动, 转动惯量为J ,开始时转台以匀角速度0ω转动,此时有一质量为m 的人站住转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为 ( A ) A.()2mR J J +ω B.()2Rm J J +ω C.20mR J ω D.0ω4、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示。
今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的? ( A )A.角速度从小到大,角加速度从大到小.B.角速度从小到大,角加速度从小到大.C.角速度从大到小,角加速度从大到小.D.角速度从大到小,角加速度从小到大.5、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动,如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度( C )A.增大B.不变C.减小 (D) 、不能确定6、在地球绕太阳中心作椭圆运动时,则地球对太阳中心的 ( B ) A.角动量守恒,动能守恒 B.角动量守恒,机械能守恒 C.角动量不守恒,机械能守恒 D.角动量守恒,动量守恒7、有两个半径相同,质量相等的细圆环A 和B ,A 环的质量分布均匀,B 环的质量分布不均匀,它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ,则 ( C )A.B A J J >;B.B A J J <;C.B A J J =;D.不能确定A J 、B J 哪个大。


刚体的简单运动习题及答案刚体的简单运动习题及答案刚体是物理学中的一个基本概念,它指的是在运动过程中形状和大小不发生改变的物体。
在学习刚体的运动时,我们可以通过一些简单的习题来加深对刚体运动的理解。
下面,我将为大家提供一些常见的刚体运动习题及答案。
习题一:平抛运动小明站在一个高处,手中拿着一个小球,以一定的初速度将球水平抛出。
假设空气阻力可以忽略不计,请问球的运动轨迹是什么形状?答案:球的运动轨迹是一个抛物线。
在平抛运动中,刚体在水平方向上做匀速直线运动,在竖直方向上受到重力的作用,所以球的轨迹是一个抛物线。
习题二:滚动运动一个圆柱体沿着水平面滚动,它的质心速度和边缘速度哪个更大?答案:质心速度和边缘速度相等。
在滚动运动中,刚体的质心沿着运动方向做匀速直线运动,而刚体的边缘点则具有线速度和角速度的叠加效果。
由于圆柱体的每个点都有相同的角速度,所以质心速度和边缘速度相等。
习题三:转动惯量一个均匀的圆盘和一个均匀的长方体,它们的质量和半径(或边长)相同,哪个的转动惯量更大?答案:圆盘的转动惯量更大。
转动惯量是刚体旋转时惯性的量度,它与刚体的质量分布有关。
由于圆盘的质量分布更加均匀,所以它的转动惯量更大。
习题四:平衡条件一个悬挂在绳子上的物体处于平衡状态,绳子与竖直方向的夹角是多少?答案:绳子与竖直方向的夹角等于物体所受的重力与绳子张力的夹角。
在平衡状态下,物体所受的重力与绳子张力必须保持平衡,即两者的合力为零。
因此,绳子与竖直方向的夹角取决于物体所受的重力与绳子张力的大小关系。
习题五:平移运动和转动运动一个刚体在平面上做平移运动时,它的转动惯量是多少?答案:在平移运动时,刚体的转动惯量为零。
平移运动是指刚体的质心沿直线运动,此时刚体没有绕任何轴心旋转,所以转动惯量为零。
通过以上习题的解答,我们可以更好地理解刚体的运动特性。
刚体的运动涉及到平抛运动、滚动运动、转动惯量和平衡条件等方面的知识,通过解答这些习题,我们可以加深对刚体运动的理解,提高解题能力。





第四章 点的运动和刚体基本运动 习题解答4-1 图示曲线规尺的杆长200==AB OA mm ,50====AE AC DE CD mm 。
杆OA 绕O 轴转动的规律为t 5πϕ=rad ,并且当运动开始时,角0=ϕ,求尺上D 点的运动方程和轨迹。
解: 已知t πϕ2.0=,故点D 的运动方程为 m m 2.0cos 200D t x π= m m 2.0sin 100D t y π=消去时间t 得到点D 的轨迹方程为11002002222=+DD y x (椭圆)4-2 图示AB 杆长l ,以t ωϕ=的规律绕B 点转动,ω为常量。
而与杆连接的滑块B 以t b a s ωsin +=的规律沿水平线作谐振动,a 、b 为常量。
求A 点的轨迹。
解: 采用直角坐标法,取图示直角坐标系O xy , 则A 点位置坐标为ϕsin l s x += ,ϕcos l y -=,即()t l b a x ωsin ++= t l y ωc o s -=. 消去时间t 得A 点轨迹方程为:2222()1()x a y b l l-+=+.(椭圆)4-3 套筒A 由绕过定滑轮B 的绳索牵引而沿导轨上升,滑轮中心到导轨的距离为l ,如图所示。
设绳索以等速0v 拉下,忽略滑轮尺寸。
求套筒A 的速度和加速度与距离x 的关系式。
解:设0=t 时,绳上C 点位于B 处,在瞬时t ,到达图示位置 则 =++=+t v l x BC AB 022常量,将上式求导,得到管套A 的速度和加速度为220d d l x xv t x v A +-==, 3220d d x l v t v a A A -==, 负号表示A A a v ,的实际方向与x 轴相反。
4-4 如图所示,半径为R 的圆形凸轮可绕O 轴转动,带动顶杆BC 作铅垂直线运动。
设凸轮圆心在A 点,偏心距e =OA ,t ωϕ=,其中ω为常量。
试求顶杆上B 点的运动方程、速度和加速度。
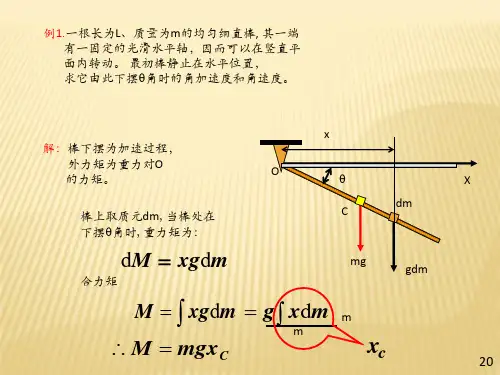
第五章 刚体的转动5-13 如图5-13(a)所示,滑轮转动惯量为0.012m kg ⋅,半径为7 cm ,物体质量为5 kg ,由一绳与倔强系数k=200 N/m 的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计,求:(1)当绳拉直弹簧无伸长时,使物体由静止而下落的最大距离;(2)物体速度达最大值的位置及最大速率.分析 下面的5-17题中将证明,如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,则由刚体和地球组成的系统机械能守恒.如果将滑轮、地球和物体与弹簧组成一个弹性系统和重力系统合成的系统,当无重力和弹性力以外的力作功的情况下,整个系统的机械能守恒,可以应用机械能守恒定律.下面的解则仅应用功能原理和力矩所作的功与刚体转动动能的关系进行计算.解 (1) 物体由静止而下落到最低点时,速度为零,位移为1x ,在此期间重力所作的功完全转换为弹簧弹性势能的增量,即21121kx mgx = m 0.49m 2008.95221=⨯⨯==k mg x (2)物体与滑轮受力如图5-13(b)所示,设物体的最大速率为0v ,此时的位移为0x ,加速度00=a ,滑轮的角加速度000==R a α,分别应用牛顿第二定律和转动定律T1aF ’T1m m g(a) (b)图5-13ma F mg =-T1αJ R F F =-)(T2T1可得此时T1F mg =,F T1= F T2,又因对于轻弹簧有0T2kx F =,则得m 0.245m 2008.950=⨯==k mg x 在此过程中,重力所作之功等于弹性势能的增量、物体动能和滑轮转动动能的增量的和,即2020200212121ωJ m kx mgx ++=v 因R00v =ω,得 m/s 31.1m/s 9.85)07.001.05(2001)(122=⨯⨯+⨯=+=mg R J m k v5-7 如图5-7(a )所示的系统中,m 1 = 50 kg ,m 2 = 40 kg ,圆盘形滑轮质量m = 16 kg ,半径R = 0.1 m ,若斜面是光滑的,倾角为30°,绳与滑轮间无相对滑动,不计滑轮轴上的摩擦,(1)求绳中张力;(2)运动开始时,m 1距地面高度为1 m ,需多少时间m 1到达地面?分析 由于存在物体运动和滑轮定轴转动,而且必须考虑圆盘形滑轮的质量,这是一个质点动力学和刚体动力学的综合问题,应该采用隔离物体法,分别m αF ’T1 F T1 m 2 m 1 F F T2a︒30m 2g m 1g(a ) (b )图5-7对运动物体作受力分析,对转动的滑轮作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 (1)各物体与滑轮受力情况如图5-7(b )所示,其中F T1= F ’T1,F T2= F ’T2,轴对滑轮的支承力F N 不产生力矩,选取物体运动方向为坐标轴正向,分别应用牛顿第二定律和转动定律,可得22121rad/s 3021)(30sin =++︒-=g mR R m m m m α N 340)(1T1=-=αR g m FN 316)30sin (2T2=+︒=αR g m F2m/s 3==αR a(2) m 1到达地面的时间为s 0.816s 3122=⨯==a h t 、5-1 一个匀质圆盘由静止开始以恒定角加速度绕过中心而垂直于盘面的定轴转动.在某一时刻,转速为10 r/s ,再转60转后,转速变为15 r/s ,试计算:(1)角加速度;(2)由静止达到10 r/s 所需时间;(3)由静止到10 r/s 时圆盘所转的圈数.分析 绕定轴转动的刚体中所有质点都绕轴线作圆周运动,并具有相同的角位移、角速度和角加速度,因此描述运动状态的物理量与作圆周运动的质点的相似.当角加速度恒定时,绕定轴转动的刚体用角量表示的运动学公式与匀加速直线运动的公式类似.解 (1) 根据题意,转速由rad/s 1021⨯=πω变为rad/s 1522⨯=πω期间的角位移rad 260πθ⨯=,则角加速度为22222122rad/s 54.6rad/s 2602)102()152(2=⨯⨯⨯-⨯=-=πππθωωα (2) 从静止到转速为rad/s 1021⨯=πω所需时间为s 9.61s 54.61021=⨯==παωt (3) t 时间内转的圈数为48261.91022122121=⨯⨯⨯===ππωππθt N 5-2 唱片在转盘上匀速转动,转速为78 r/min ,由开始到结束唱针距转轴分别为15 cm 和7.5 cm ,(1)求这两处的线速度和法向加速度;(2)在电动机断电以后,转盘在15 s 内停止转动,求它的角加速度及转过的圈数.分析 绕定轴转动的刚体中所有质点具有相同的角位移、角速度和角加速度,但是线速度、切向加速度和法向加速度等线量则与各质点到转轴的距离有关.角量与线量的关系与质点圆周运动的相似.解 (1) 转盘角速度为rad/s 8.17rad/s 60278=⨯=πω,唱片上m 15.01=r 和m 075.02=r 处的线速度和法向加速度分别为m/s 1.23m/s 15.017.811=⨯==r ωv222121n m/s 10.0m/s 15.017.8=⨯==r ωam/s .6130m/s 075.017.822=⨯==r ωv222222n m/s .015m/s 075.017.8=⨯==r ωa(2) 电动机断电后,角加速度为22rad/s 545.0rad/s 1517.800-=-=-=t ωα 转的圈数为 75.921517.8212212=⨯⨯===πωππθt N 5-3 如图5-3所示,半径r 1 = 30 cm 的A 轮通过皮带被半径为r 2 = 75 cm 的B 轮带动,B 轮以π rad/s 的匀角加速度由静止起动,轮与皮带间无滑动发生,试求A 轮达到3000 r/min 所需要的时间. 分析 轮与皮带间无滑动,则同一时刻,两轮边缘的线速度相同,均等于皮带的传送速度;两轮边缘的切向加速度也相同,均等于皮带的加速度.解 设A 、B 轮的角加速度分别为A α、B α,由于两轮边缘与皮带连动,切向加速度相同,即2B 1A r r αα=则 B 12A ααr r = A 轮角速度达到rad/s 6030002⨯=πω所需要的时间为 s 40s 75.06030.0300022B 1A =⨯⨯⨯⨯===ππαωαωr r tB A r 1 r 2图5-35-4 在边长为b 的正方形的顶点上,分别有质量为m 的四个质点,求此系统绕下列转轴的转动惯量:(1)通过其中一质点A ,平行于对角线BD 的转轴,如图5-4所示.(2)通过A 垂直于质点所在平面的转轴.分析 由若干质点组成的质点系对某转轴的转动惯量等于各质点对该转轴转动惯量的叠加.每一质点对转轴的转动惯量等于它的质量与其到转轴的垂直距离平方的乘积. 解 (1)因质点B 和D 到转轴的垂直距离A 2B 和A 1D 为a 22,质点C 到转轴的垂直距离AC 为a 2,而质点A 位于转轴上,则系统对通过A 点平行于BD 的转轴的转动惯量为()222132222ma am a m J =+⎪⎪⎭⎫ ⎝⎛=(2) 因质点B 和D 到转轴的垂直距离AB 和AD 为a ,质点C 到转轴的垂直距离AC 为a 2,而质点A 位于转轴上,则系统对通过A 垂于质点所在平面转轴的转动惯量为()2222422ma a m ma J =+=5-5 求半径为R ,质量为m 的均匀半圆环相对于图5-5中所示轴线的转动惯量.分析 如果刚体的质量连续分布在一细线上,可用质量线密度描述其分布情况,如果分布是均匀的,则质量线密度λ为常量.在刚体上取一小段线元l d ,质量为l d λ,对转轴的转动惯量为l r d 2λ,其中该线元AA 2B图5-4R图5-5到转轴的距离r 与线元在刚体上的位置有关.整个刚体的转动惯量就是刚体上所有线元转动惯量的总和,即所取线元的转动惯量对刚体分布的整个区域积分的结果.解 均匀半圆环的质量线密度为Rm πλ=,在半圆环上取一小段圆弧作为线元θd d R l =,质量为 θπθπλd d d d m R R m l m === 此线元到转轴的距离为θsin R r =,对轴线的转动惯量为m r d 2,则整个半圆环的转动惯量为2022221d sin d mR m R m r J =⋅==⎰⎰θπθπ 5-6 一轻绳跨过滑轮悬有质量不等的二物体A 、B ,如图5-6(a)所示,滑轮半径为20 cm ,转动惯量等于2m kg 50⋅,滑轮与轴间的摩擦力矩为m N 198⋅.,绳与滑轮间无相对滑动,若滑轮的角加速度为2rad/s 362.,求滑轮两边绳中张力之差. 分析 由于定轴转动的刚体的运动规律遵从转动定律,因此对于一个定轴转动的滑轮来说,仅当其质量可以忽略,转动惯量为零,滑轮加速转动时跨越滑轮的轻绳两边的张力才相等.这就是在质点动力学问题中通常采用的简化假设.在掌握了转动定律后,不应该再忽略滑轮质量,通常将滑轮考虑为质量均匀分布的圆盘,则跨越滑轮的轻绳两边的张力对转轴的合力矩是滑轮产生角加速度的原因.解 滑轮所受力和力矩如图5-6(b)所示,其中跨越滑轮的轻绳两边的张力分别为F T1和F T2,轴的支承力F N 不产生力矩,由转动定律可得fF T1 F T2(a) (b)图5-6αJ M R F F =--f T2T1)()(1f T2T1M J RF F +=-α N 101.08N )1.9836.250(2.01 3⨯=+⨯⨯= 5-7 如图5-7(a )所示的系统中,m 1 = 50 kg ,m 2 = 40 kg ,圆盘形滑轮质量m = 16 kg ,半径R = 0.1 m ,若斜面是光滑的,倾角为30°,绳与滑轮间无相对滑动,不计滑轮轴上的摩擦,(1)求绳中张力;(2)运动开始时,m 1距地面高度为1 m ,需多少时间m 1到达地面?分析 由于存在物体运动和滑轮定轴转动,而且必须考虑圆盘形滑轮的质量,这是一个质点动力学和刚体动力学的综合问题,应该采用隔离物体法,分别对运动物体作受力分析,对转动的滑轮作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 (1)各物体与滑轮受力情况如图5-7(b )所示,其中F T1= F ’T1,F T2= F ’T2,轴对滑轮的支承力F N 不产生力矩,选取物体运动方向为坐标轴正向,分别应用牛顿第二定律和转动定律,可得m αF ’T1 F T1 m 2 m 1 F F T2a︒30m 2g m 1g(a ) (b )图5-7由于物体的加速度等于滑轮边缘的线速度,则αR a =,与以上各式联立解得22121rad/s 3021)(30sin =++︒-=g mR R m m m m α N 340)(1T1=-=αR g m FN 316)30sin (2T2=+︒=αR g m F2m/s 3==αR a(2) m 1到达地面的时间为s 0.816s 3122=⨯==a h t 5-8 飞轮质量为60 kg ,半径为0.25 m ,当转速为1000 r/min 时,要在5 s 内令其制动,求制动力F ,设闸瓦与飞轮间摩擦系数μ=0.4,飞轮的转动惯量可按匀质圆盘计算,闸杆尺寸如图5-8所示.分析 制动力F 作用在闸杆上,闸杆在制动力和飞轮的正压力的力矩作用下达到平衡,转动轴在墙上,这是刚体在力矩作用下的平衡问题.由于二力的力臂已知,应该求出闸杆与飞轮之间的正压力.飞轮受到闸杆的正压力、闸瓦与飞轮间摩擦力和轴的支承力作用,其中闸杆的正压力和轴的支承力的力矩为零,在闸瓦与飞轮间摩擦力的力矩作用下制动,应用转动定律可以求出摩擦力矩,然后由摩擦力与正压力关系可以求出闸杆与飞轮之间的正压力.F图5-8解 以飞轮为研究对象,飞轮的转动惯量为221mR J =,制动前角速度为rad/s 6010002⨯=πω,制动时角加速度为tωα-=.制动时闸瓦对飞轮的压力为F N ,闸瓦与飞轮间的摩擦力N f F F μ=,应用转动定律,得αα2f 21mR J R F ==- 则 t mR F μω2N =以闸杆为研究对象.在制动力F 和飞轮对闸瓦的压力-F N 的力矩作用下闸杆保持平衡,两力矩的作用力臂分别为m )75.050.0(+=l 和m 50.01=l ,则有01N =-l F FlN 157N 6054.021000225.06075.050.050.021N 1=⨯⨯⨯⨯⨯⨯⨯+===πμωt mR l l F l l F 5-9 一风扇转速为900 r/min ,当马达关闭后,风扇均匀减速,止动前它转过了75转,在此过程中制动力作的功为44.4 J ,求风扇的转动惯量和摩擦力矩.分析 合外力矩对刚体所作的功等于刚体的转动动能的增量.制动过程中风扇只受摩擦力矩作用,而且由于风扇均匀减速,表明摩擦力矩为恒定值,与风扇角位移的乘积就是所作的功.解 设制动摩擦力矩为M ,风扇转动惯量为J ,止动前风扇的角位移N πθ2=,摩擦力矩所作的功为N M M W πθ2⋅-=-=摩擦力矩所作的功应等于风扇转动动能的增量,即2210ωJ W -= 则 2222m kg 01.0m kg )60/2900()4.44(22⋅=⋅⨯-⨯-=-=πωWJ m N 0.0942m N 7524.442⋅=⋅⨯--=-=ππN W M5-10 如图5-10(a )所示,质量为24 kg 的鼓形轮,可绕水平轴转动,一绳缠绕于轮上,另一端通过质量为5 kg 的圆盘形滑轮悬有10 kg 的物体,当重物由静止开始下降了0.5 m 时,求:(1)物体的速度;(2)绳中张力.设绳与滑轮间无相对滑动.分析 这也是一个质点动力学和刚体动力学的综合问题,鼓形轮和滑轮都视为圆盘形定轴转动的刚体,应该采用隔离物体法,分别对运动物体作受力分析,对刚体作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 各物体受力情况如图5-10(b )所示,其中F T1= F ’T1,F T2= F ’T2,鼓形轮的转动惯量为2121R m ,圆盘形滑轮的转动惯量为2221r m ,分别应用牛顿第二定律和转动定律,可得ma F mg =-T2222T1T221)(αr m r F F =- 121T121αR m R F = (1) 绳与滑轮间无相对滑动,物体的加速度等于鼓形轮和滑轮边缘的切向加速度,即12ααR r a ==.重物由静止开始下降了h = 0.5 m 时,速度ah 2=v ,由以上各式得αT1 F 2α ’T2 a F T2m g(a ) (b )图5-10m/s 2m/s )524(21105.08.9102)(212221=+⨯+⨯⨯⨯=++==m m m mgh ah v (2)绳中张力为N 48N 5241028.924102211T1=++⨯⨯⨯=++=m m m g mm F N 85N 5241028.9)524(102)(2121T2=++⨯⨯+⨯=+++=m m m g m m m F 5-11 一蒸汽机的圆盘形飞轮质量为200 kg ,半径为1 m ,当飞轮转速为120 r/min 时关闭蒸汽阀门,若飞轮在5 min 内停下来,求在此期间飞轮轴上的平均摩擦力矩及此力矩所作的功.分析 制动过程中飞轮只受摩擦力矩作用,该摩擦力矩不一定为恒定值,但是由于只需求平均摩擦力矩,因此可以假设飞轮均匀减速,由已知条件求出平均角加速度,再应用转动定律求出平均摩擦力矩.解 飞轮转动惯量为221mR J =,关闭蒸汽阀门后t = 5 min 内的平均角加速度为t00ωα-=,应用转动定律,平均摩擦力矩 m N 194m N 60560/212012002121202⋅-=⋅⨯⨯⨯⨯⨯-=-==.t mR J M πωα 在此期间平均摩擦力矩所作的功等于飞轮转动动能的增量J 7896J )60/2120(12002121 21212102220220-=⨯⨯⨯⨯⨯-=⋅-=-=πωωm R J W 负号表示平均摩擦力矩作负功,方向与飞轮旋转方向相反.5-12 长为85 cm 的均匀细杆,放在倾角为45°的光滑斜面上,可以绕过上端点的轴在斜面上转动,如图5-12(a)所示,要使此杆实现绕轴转动一周,至少应给予它的下端多大的初速度?分析 细杆在斜面上转动,斜面的支承力与转轴平行,转轴的支承力通过转轴,它们的力矩都为零,只有重力在转动平面内分量的力矩作功.解 如图5-12(b)所示,杆所受重力在转动平面内的分量为︒45sin mg ,当杆与初始位置的夹角为θ时,重力分量对转轴的力矩为θsin 2145sin l mg ⋅︒,此时若杆有角位移θd ,则重力矩所作的元功为θθd sin 2145sin d ⋅⋅︒=l mg W 杆从最低位置到最高位置重力矩所作的功为︒-=⋅⋅︒-==⎰⎰45sin d sin 2145sin d 0mgl l mg W W πθθ 重力矩所作的功等于此期间杆的转动动能的增量2021045sin ωJ mgl -=︒- 其中231ml J =,t00v =ω,则 m/s 5.94m/s 45sin 85.08.9645sin 60=︒⨯⨯⨯=︒=gl v5-13 如图5-13(a)所示,滑轮转动惯量为0.012m kg ⋅,半径为7 cm ,物体质量为5 kg ,由一绳与倔强系数k=200 N/m 的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计,求:(1)当绳拉直弹簧无伸长时,使物体由静止而下落的最大距离;(2)物体速度达最大值的位置及最大速率.v 0 ︒45 (a) (b) 图5-12分析 下面的5-17题中将证明,如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,则由刚体和地球组成的系统机械能守恒.如果将滑轮、地球和物体与弹簧组成一个弹性系统和重力系统合成的系统,当无重力和弹性力以外的力作功的情况下,整个系统的机械能守恒,可以应用机械能守恒定律.下面的解则仅应用功能原理和力矩所作的功与刚体转动动能的关系进行计算.解 (1) 物体由静止而下落到最低点时,速度为零,位移为1x ,在此期间重力所作的功完全转换为弹簧弹性势能的增量,即21121kx mgx = m 0.49m 2008.95221=⨯⨯==k mg x (2)物体与滑轮受力如图5-13(b)所示,设物体的最大速率为0v ,此时的位移为0x ,加速度00=a ,滑轮的角加速度000==R a α,分别应用牛顿第二定律和转动定律ma F mg =-T1αJ R F F =-)(T2T1可得此时T1F mg =,F T1= F T2,又因对于轻弹簧有0T2kx F =,则得m 0.245m 2008.950=⨯==k mg x 在此过程中,重力所作之功等于弹性势能的增量、物体动能和滑轮转动动能T1aF ’T1m m g(a) (b)图5-13的增量的和,即2020200212121ωJ m kx mgx ++=v 因R00v =ω,得 m/s 31.1m/s 9.85)07.001.05(2001)(122=⨯⨯+⨯=+=mg R J m k v5-14 圆盘形飞轮A 质量为m ,半径为r ,最初以角速度ω0转动,与A 共轴的圆盘形飞轮B 质量为4m ,半径为2r ,最初静止,如图5-14所示,两飞轮啮合后,以同一角速度ω转动,求ω及啮合过程中机械能的损失.分析 当物体系统所受的合外力矩为零时,系统的角动量守恒,在此过程中,由于相互作用的内力作功,机械能一般不守恒.解 以两飞轮组成的系统为研究对象,由于运动过程中系统无外力矩作用,角动量守恒,有ωωω2202)2(4212121r m mr mr += 得 0171ωω= 初始机械能为2022021412121ωωmr mr W =⋅= 啮合后机械能为2022222241171)2(421212121ωωωmr r m mr W =⋅+⋅= 则机械能损失为1202211716411716W mr W W W ==-=∆ω 5-15 一人站在一匀质圆板状水平转台的边缘,转台的轴承处的摩擦可忽略A图5-14不计,人的质量为m ’,转台的质量为10 m ’,半径为R .最初整个系统是静止的,这人把一质量为m 的石子水平地沿转台的边缘的切线方向投出,石子的速率为v (相对于地面).求石子投出后转台的角速度与人的线速度.分析 应用角动量守恒定律,必须考虑定律的适用条件,即合外力矩为零.此外还应该注意到,定律表达式中的角动量和角速度都必须是对同一惯性参考系选取的,而转动参考系不是惯性参考系.解 以人、转台和石子组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,设转台角速度ω的转向与投出的石子速度v 方向一致,初始时系统角动量为零,得0=+v mR J ω 人和转台的转动惯量为221021R m R m J '+'=,代入上式后得 Rm m '-=6v ω 人的线速度 mm R '-=='6v v ω 其中负号表示转台角速度转向和人的线速度方向与假设方向相反.5-16 一人站立在转台上,两臂平举,两手各握一个m = 4 kg 的哑铃,哑铃距转台轴r 0 = 0.8 m ,起初,转台以ω0 = 2π rad/s 的角速度转动,然后此人放下两臂,使哑铃与轴相距r = 0.2 m ,设人与转台的转动惯量不变,且J = 52m kg ⋅,转台与轴间摩擦忽略不计,求转台角速度变为多大?整个系统的动能改变了多少?分析 角动量守恒定律是从定轴转动的刚体导出的,却不但适用与刚体,而且适用于绕定轴转动的任意物体和物体系统.解 以人、转台和哑铃组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,有ωω)2()2(2020mr J mr J +=+rad/s 12.0rad/s 22.04258.042522220220=⨯⨯⨯+⨯⨯+=++=πωωmr J mr J 动能的增量为J183 J )2()8.0425(21J 12)2.0425(21 )2(21)2(2122222020220=⨯⨯⨯+⨯-⨯⨯⨯+⨯=+-+=-=∆πωωmr J mr J W W W 5-17 证明刚体中任意两质点相互作用力所作之功的和为零.如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,试证明它的机械能守恒.分析 在刚体动力学中有很多涉及重力矩作功的问题,如果能证明当只有重力矩作功时刚体和地球组成的系统机械能守恒,就能应用机械能守恒定律,而且还可以用刚体的质心的势能代替整个刚体中所有质点势能的总和,使求解过程大大简化. 证 刚体中任意两质点相互作用力沿转轴方向的分量对定轴转动不起作用,而在垂直于转轴的平面内的分量F 和-F 大小相等,方向相反,作用在一条直线上,如图5-17所示.设F 与转轴的垂直距离为ϕsin r ,则当刚体有微小角位移θd 时,力F 所作的功为θϕd sin Fr ,而其反作用力-F 所作的功为θϕd sin Fr -,二者之和为零,即刚体中任意两质点相互作用力所作之功的和为零.绕定轴转动的刚体除受到轴的支承力外仅受重力作用,刚体中任意质点则受到内力和重力作用,当刚体转动时,因为已经证明了任意两质点相互作用内力所作之功的和为零,则刚体中各质点相互作用力所作的总功为零,而且轴的支承力-F图5-17也不作功,就只有重力作功,因此机械能守恒.5-18 一块长m 50.0=L ,质量为m '=3.0 kg 的均匀薄木板竖直悬挂,可绕通过其上端的水平轴无摩擦地自由转动,质量m =0.1kg 的球以水平速度m/s 500=v 击中木板中心后又以速度m/s 10=v 反弹回去,求木板摆动可达到的最大角度.木板对于通过其上端轴的转动惯量为231L m J '= . 分析 质点的碰撞问题通常应用动量守恒定律求解,有刚体参与的碰撞问题则通常应用角动量守恒定律求解.质点对一点的角动量在第四章中已经讨论过,当质点作直线运动时,其角动量的大小是质点动量和该点到质点运动直线的垂直距离的乘积.解 对球和木板组成的系统,在碰撞瞬间,重力对转轴的力矩为零,且无其他外力矩作用,系统角动量守恒,碰撞前后球对转轴的角动量分别为021v mL 和v mL 21-,设碰后木板角速度为ω,则有 ωJ mL mL +-=v v 21210 设木板摆动可达到的最大角度为θ,如图5-18所示,木板摆动过程中只有重力矩作功,重力矩所作的功应等于木板转动动能的增量,即)1(cos 21d sin 2121002-'=⋅'-=-⎰θθθωθgL m L g m J (1) 由以上两式得388.050.08.90.34)1050(1.0314)(31cos 2222202=⨯⨯⨯+⨯⨯-='+-=gL m m v v θ ︒==19.67)388.0arccos(θ根据5-17的结果,由于木板在碰撞后除受到轴的支承力外仅受重力作用,v mm ’g图5-18它的机械能守恒,取木板最低位置为重力势能零点,达到最高位置时它的重力势能应等于碰撞后瞬间的转动动能,也可以得到(1)式.5-19 半径为R 质量为m '的匀质圆盘水平放置,可绕通过圆盘中心的竖直轴转动.圆盘边缘及R /2处设置了两条圆形轨道,质量都为m 的两个玩具小车分别沿二轨道反向运行,相对于圆盘的线速度值同为v .若圆盘最初静止,求二小车开始转动后圆盘的角速度.分析 当合外力矩为零时,应用角动量守恒定律应该注意到表达式中的角动量和角速度都是对同一惯性参考系选取的.转动参考系不是惯性参考系,所以小车对圆盘的速度和角动量必须应用相对运动速度合成定理转换为对地面的速度和角动量.解 设两小车和圆盘的运动方向如图5-19所示,以圆盘的转动方向为正向,外轨道上小车相对于地面的角动量为)(v -ωR mR ,内轨道上小车相对于地面的角动量为)21(21v +ωR R m ,圆盘的角动量为ωω221R m J '=.对于两小车和圆盘组成的系统,外力对转轴的力矩为零,角动量守恒,得ωωω221)21(21)(R m R R m R mR '+++-v v R m m m )25(2'+=v ω vωv图5-19。
第四章 点的运动和刚体基本运动本章要点 一、点的运动1 点运动位置的确定的三种方法 ⅰ)矢量法:)(t r r =;ⅱ)直角坐标法:)(t x x =,)(t y y =,)(t z z =; ⅲ)弧坐标法(轨迹已知):)(t s s =. 2 点的速度与加速度的矢量表示速度 t d d r v =, 加速度 22td d t d d rv a ==. 3 点的速度与加速度的直角坐标表示 速度在各坐标轴上的投影为t x v d d =x , t y v d d =y , tzv d d =z . 速度的大小和方向余弦为⎪⎭⎪⎬⎫===++=v v v v v v v v v v z y x 2z2y 2x ),cos(,),cos(,),cos(k v j v i v加速度在各坐标轴上的投影为222222d d d d d d d d d d d d dtz t v a ,t y t v a ,t x t v a z z y y x x ====== 加速度的大小和方向余弦分别为⎪⎭⎪⎬⎫===++=a a a a a a a a a a z y x 2z2y 2x ),cos(,),cos(,),cos(k a j a i a4 点的速度与加速度的弧坐标表示点的速度 τv td sd =, 切向加速度 ττa 22td sd t d d ==v τ;法向加速度 n a ρv 2n =,其中τ为切线单位矢量,指向弧坐标增加的方向;n 表示主法线正向的单位矢量,指向曲率中心(即指向曲线凹的一方)。
全加速度为 n τa a a+=全加速度a 的大小和它与法线间夹角的正切分别为2n 2τa a a +=,()nτtg a a =n a,解题要领:1 确定动点,根据题意是选择矢量法、直角坐标法还是弧坐标法,三种方法各有所长.2 从点的运动方程出发求点的速度和加速度是对时间的求导运算;反之,也可以从加速度出发求速度和运动方程,或从速度出发求运动方程,这是积分运算,但结果都不唯一 ,积分常数需要用初始条件来确定。
第四章 点的运动和刚体基本运动本章要点 一、点的运动1 点运动位置的确定的三种方法 ⅰ)矢量法:)(t r r =;ⅱ)直角坐标法:)(t x x =,)(t y y =,)(t z z =; ⅲ)弧坐标法(轨迹已知):)(t s s =. 2 点的速度与加速度的矢量表示速度 t d d r v =, 加速度 22td d t d d rv a ==. 3 点的速度与加速度的直角坐标表示 速度在各坐标轴上的投影为t x v d d =x , t y v d d =y , tzv d d =z . 速度的大小和方向余弦为⎪⎭⎪⎬⎫===++=v v v v v v v v v v z y x 2z2y 2x ),cos(,),cos(,),cos(k v j v i v加速度在各坐标轴上的投影为222222d d d d d d d d d d d d dtz t v a ,t y t v a ,t x t v a z z y y x x ====== 加速度的大小和方向余弦分别为⎪⎭⎪⎬⎫===++=a a a a a a a a a a z y x 2z2y 2x ),cos(,),cos(,),cos(k a j a i a4 点的速度与加速度的弧坐标表示点的速度 τv td sd =, 切向加速度 ττa 22td sd t d d ==v τ;法向加速度 n a ρv 2n =,其中τ为切线单位矢量,指向弧坐标增加的方向;n 表示主法线正向的单位矢量,指向曲率中心(即指向曲线凹的一方)。
全加速度为 n τa a a+=全加速度a 的大小和它与法线间夹角的正切分别为2n 2τa a a +=,()nτtg a a =n a,解题要领:1 确定动点,根据题意是选择矢量法、直角坐标法还是弧坐标法,三种方法各有所长.2 从点的运动方程出发求点的速度和加速度是对时间的求导运算;反之,也可以从加速度出发求速度和运动方程,或从速度出发求运动方程,这是积分运算,但结果都不唯一 ,积分常数需要用初始条件来确定。
3 从直角坐标形式的运动方程出发计算切向加速度、法向加速度、曲率半径、弧坐标的过程点的速度:222z y x v v v v ++=, 点的加速度: 222z y x a a a a ++=,切向加速度: td d t v =a , 法向加速度:2t 2n a a a -=, 曲率半径:n2a v =ρ, 弧坐标:⎰=t t v s 0d .二、刚体的平移刚体在运动过程中,其上任意一条直线始终平行于它的初始位置,刚体的这种运动称为平移。
具有性质:刚体平移时,其上各点的轨迹形状相同,在同一瞬时,各点的速度和加速度也相同。
刚体的平移问题可以归结为点的运动问题. 三、刚体的定轴转动 1 刚体定轴转动的整体描述转动方程 )(t ϕϕ=, 角速度 td d ϕω=, 角加速度 22td d t d d ϕωα==. 匀速转动(ω为常量),则 t ωϕϕ+=0,匀变速转动(α为常量),则t αωω+=0,20021t t αωϕϕ++=. 2 角速度和角加速度的矢量表示k ωω=, k αα=,其中k 为沿转动轴方向的单位矢量。
3 转动刚体上各点的速度和加速度距转轴距离为R 的点的速度为 R ωv =,切向加速度: αR a =t , 法向加速度: 22n ωR Rv a == 全加速度a 的大小: 42ωα+=R a加速度a 的方向: 22nτtg ωαR ωR αa a ===β.用矢积表示刚体上各点的速度和加速度点的速度 r ωv ⨯= ,切向加速度r αa ⨯=τ, 法向加速度 v ωa ⨯=n .解题要领1 利用三角函数关系写出转动方程,对时间求导一次得到角速度,求导两次得到角加速度方程,角速度或角加速度为正,表明其转向是与角度增加的方向一致;角速度和角加速度同号(异号)表明刚体作加(减)速转动。
2 定轴转动刚体上点的切向和法向加速度的计算公式是点作曲线运动时的特例,不可混淆。
第四章 点的运动和刚体基本运动 习题解答4-1 图示曲线规尺的杆长200==AB OA mm ,50====AE AC DE CD mm 。
杆OA 绕O 轴转动的规律为t 5πϕ=rad ,并且当运动开始时,角0=ϕ,求尺上D 点的运动方程和轨迹。
解: 已知t πϕ2.0=,故点D 的运动方程为mm 2.0cos 200D t x π=mm2.0sin 100D t y π=消去时间t 得到点D 的轨迹方程为题 4-1图11002002222=+DD y x (椭圆) 4-2 图示AB 杆长l ,以t ωϕ=的规律绕B 点转动,ω为常量。
而与杆连接的滑块B 以t b a s ωsin +=的规律沿水平线作谐振动,a 、b 为常量。
求A 点的轨迹。
解: 采用直角坐标法,取图示直角坐标系O xy , 则A 点位置坐标为ϕsin l s x += ,ϕcos l y -=,即()t l b a x ωsin ++= t l y ωc o s -=. 消去时间t 得A 点轨迹方程为:2222()1()x a y b l l-+=+.(椭圆)4-3 套筒A 由绕过定滑轮B 的绳索牵引而沿导轨上升,滑轮中心到导轨的距离为l ,如图所示。
设绳索以等速0v 拉下,忽略滑轮尺寸。
求套筒A 的速度和加速度与距离x 的关系式。
解:设0=t 时,绳上C 点位于B 处,在瞬时t ,到达图示位置 则 =++=+t v l x BC AB 022常量,将上式求导,得到管套A 的速度和加速度为22d d l x xv t x v A +-==, 3220d d x lv t v a A A -==,负号表示A A a v ,的实际方向与x 轴相反。
4-4 如图所示,半径为R 的圆形凸轮可绕O 轴转动,带动顶杆BC 作铅垂直线运动。
设凸轮圆心在A 点,偏心距e =OA ,t ωϕ=,其中ω为常量。
试求顶杆上B 点的运动方程、速度和加速度。
解:以O 点为原点建立坐标系,由余弦定理可得2222cos AB OA OB OA OB t ω=+-⋅⋅其中OA=e ,AB=R ,设B y =OB 代入上式 可以得到 0cos 222B 2B =-+-R e t ey y ω, 解出2)(4)cos 2(cos 2222B R e t e t e y --+=ωω题4-2图题4-4图题4-3图t e R t e ωω222sin cos -+= )sin 22sin (sin d d 222te R te t e t y v B B ωωωω-+-==))sin (4sin sin 2cos (cos d d 2322222222t e R te e R t e t e t v a B B ωωωωωω-+-+-==. 4-5 若将题4-4中的顶杆换成平底的物块M ,其余条件不变。
试求物块上B 点的运动方程、速度和加速度。
解:由右图所示t e R y B ωcos +=,t e dtdy v BB ωωsin -==, t e dtdv a BB ωωcos 2==. 4-6 图示a 、b 、c 三种机构,已知机构尺寸h 和杆OA 与铅直线的夹角t ωϕ=,其中ω为常量,分析并比较它们的运动:1)穿过小环M 的杆OA 绕O 轴转动,同时拨动小环沿水平导杆滑动,求小环的速度和加速度。
2)绕O 轴转动的杆OA ,推动物块M 沿水平面滑动,求物块M 上一点的速度和加速度。
3)杆OA 绕O 轴转动时,通过套在杆上的套筒M 带动杆MN 沿水平轨道运动,求MN 上一点的速度和加速度。
a) b) c)题 4-6图解:经分析图a)、b) 、c) 中M 点速度和加速度相同。
以O 为原点,水平方向为x 轴,竖直方向为y 轴。
对图在a)、 b) 、c) 中M 点都有题4-5图t h h x ωϕtg tg ⋅=⋅=, t h x v ωω2c o s == , tt h x a ωωω32cos sin 2== . 4-7 图示滑道连杆机构。
已知10.BO =m ;10.OA =m ,滑道连杆BC 绕轴B 按t 10=ϕ的规律转动(ϕ以rad 计)。
试求滑块A 的速度和加速度。
解: 如右图所示。
以B 为极点和BO 为极轴建立极坐标系,则A 点的运动方程为 ()t OA 10cos 2⋅⋅=ρ , t 10=ϕ.A 点的速度为()t OA dt d v 10sin 20⋅⋅-==ρρ,()t OA dtd v 10cos 20⋅⋅==ϕρϕ, s m 220222==+=OA v v v ϕρ.A 点的加速度为()t OA tt a 10cos 400)d d (d d 222⋅⋅-=-=ϕρρρ,()t OA tt a 10sin 4)d d (d d 12⋅⋅-==ϕρρϕ. s m 4022=+=ϕρa a a .也可以用直角坐标法求解,并求出A 点地切向和法向加速度。
4-8 如图所示,一直杆以t 0ωϕ=绕其固定端O 转动,其中0ω为常量。
沿此杆有一滑块以匀速0v 滑动。
设运动开始时,杆在水平位置,滑块在O 点,试求滑块的轨迹(以极坐标表示)。
解: 以O 为极点,水平方向为极轴,点M 的运动方程为t v 0=ρ, t 0ωϕ=消去时间t ,得到滑块以极坐标表示的轨迹方程为ϕωρ0v =.4-9 点在平面上运动,其轨迹的参数方程为题4-7图题4-8图()m 32sintx π=()m 34sin4ty π+=,设0=t 时,0=s ;坐标s 的起点和0=t 时点的位置一致,s 的正方向相当于x 增大的方向。
试求轨迹的直角坐标方程)( x f y =、点沿轨迹运动的方程)( g t s =、点的速度和切向加速度与时间的函数关系。
解:由运动方程消去t ,得轨迹方程:42+=x y ,(22<<-x )0=t 时,由 t ty x s d 3cos203d d d 22ππ⋅⋅=+=,积分得点的运动方程t s 3s i n 472.4π=; 点的速度和加速度在轨迹切线上的投影为:()m 3cos 683.4tsv π== , t va t 3sin 904.4π-== ()2m . 4-10 点沿平面曲线轨迹x e y =向x 、y 增大的方向运动,其中x 、y 的单位皆为m ,速度大小为常量m/s 12=v 。
求动点经过m 1=y 处时,其速度和加速度在坐标轴上的投影。
解:点的切向加速度和法向加速度为0==dt dv a t , ρ2v a n =;式中 y y '''+=232)1(ρ, x e x y y ==d d , xe xy y ==22d d 当1=y 时, 0=x ,1=y,1=y有22=ρ, oy 45arctan '==θ,2362==ρv a n s m∴ 当m 1=y 时点的速度和加速度在坐标轴上的投影为:2x y v v m s === 2s m 3622-=-=n x a a ,2m 3622==n y a a4-11 如图所示,曲柄CB 以等角速度0ω绕C 轴转动,其转动方程为t 0ωϕ=。