当前位置：文档之家 › 第六章刚体的基本运动习题解答

第六章刚体的基本运动习题解答

  • 格式：docx
  • 大小：40.23 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

理论力学

理论力学

| a全 || an a | an a R 2 w 4
2 2
a R t g 2 2 an w R w
21
结论: ① v方向与w 相同时为正 , R ,与 R 成正比。
②各点的全加速度方向与各点转动半径夹角θ都一致,且 小于90o , 在同一瞬间的速度和加速度的分布图为:
习题课
35
匀 速 直 匀 a=C 线 变 运 动 变 dv a 速 dt 曲 线 运 动 匀 速 匀 变 变 速 0
a 0
点的运动(刚体平动) 加速度 v an a 0 0 v C 0 0 a =C
v v0 at
s
s f ( t ) vt
1 s v0 t at 2 2
1
第六章 刚体的基本运动
§6–1 刚体的平行移动
§6–2 刚体的定轴转动 §6–3 定轴转动刚体内各点的速度与加速度 §6–4 绕定轴转动刚体的传动问题 §6–5 角速度与角速度的矢量表示 点的速度与加速度的矢积表示 习题课
2
由于研究对象是刚体,所以运动中要考虑 其本身形状和尺寸大小,又由于刚体是几何形 状不变体,所以研究它在空间的位置就不必一 个点一个点地确定,只要根据刚体的各种运动 形式,确定刚体内某一个有代表性的直线或平 面的位置即可。
π 0l 16
v (m· s－1)
0
14
§6-2
刚体的定轴转动
一.刚体定轴转动的特征及其简化 当刚体运动时，如其上（或其延展部分）有一
条直线始终保持不动，这种运动称为刚体的定轴转
动。该固定不动的直线称为转轴。 特点:有一条不变的线称为转轴,其余各点都在垂
直于转轴的平面上做圆周运动,圆心在该平面与转

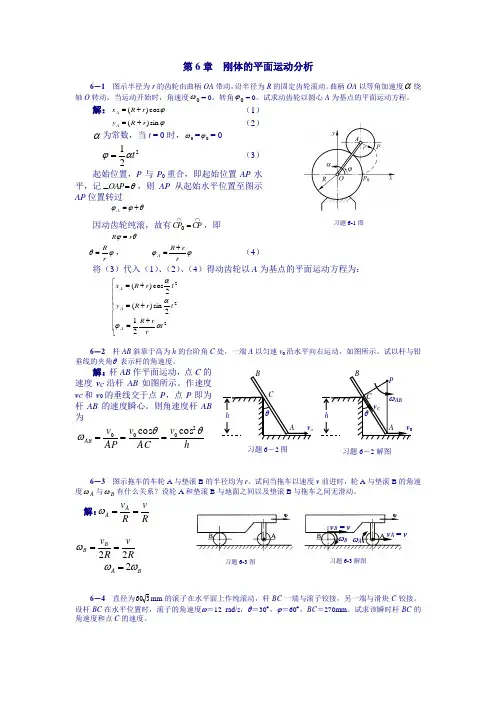
理论力学课后习题答案-第6章--刚体的平面运动分析

理论力学课后习题答案-第6章--刚体的平面运动分析

第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。

试求动齿轮以圆心A 为基点的平面运动方程。

解：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。

试以杆与铅垂线的夹角θ 表示杆的角速度。

解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。

作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。

则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。

试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。

解：RvR v A A ==ωR v R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。

设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。

试求该瞬时杆BC 的角速度和点C 的速度。

hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6－2图PωABv CABCv ohθ习题6－2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解：杆BC 的瞬心在点P ，滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6－5 在下列机构中，那些构件做平面运动，画出它们图示位置的速度瞬心。

大物第六七节习题册答案

大物第六七节习题册答案

由机械能守恒定律
E0 Ex
解出
k mg sin 2 Ek Ek 0 ( x ) 2 k
6 设想有两个自由质点，其质量分别为m1和m2，它们之间的相互作用符
合万有引力定律。开始时，两质点间的距离为l，它们都处于静止状态
试求当它们的距离变为1/2 l时，两质点的速度各为多少？
• 解:两自由质点组成的系统在自身的引力场中运动时，系 统的动量和机械能均守恒。 设两质点的间距变为L/2


2
1
1 2 Md ( J ) = 2
1 1 2 J 2 J 12 2 2
合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。
１）质点对固定点的角动量 L r mv
角动量是矢量，角动量L的方向垂直 于r和mv 所组成的平面，其指向可用 右手螺旋法则确定。
v v v
2 x
2 y

答案：B
2
1
1 1 2 2 F .d r mv2 mv1 2 2
• 2 一质点在几个外力同时作用下运动时， 下述哪种说法正确？ （ ） （A）质点的动量改变时，质点的动能一定改 变。 （B）质点的动能不变时，质点的动量也一定 不变。 （C）外力的冲量是零，外力的功一定为零。 （D）外力的功为零，外力的冲量一定为零。 解析：结果为C
时，它们的速度分别为v1及v2则有
m1v1 m2v2 0
（1）
- Gm1m2 1 1 2Gm1m2 2 m1v12 m2v2 l 2 2 l 联立（1） （2）解得：
（2）
v1 m2
2G l (m1 m2 )
v2 m1
2G l (m1 m2 )

刚体习题和答案

刚体习题和答案

作业5 刚体力学♫刚体：在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速，t ＝0时角速度为05rad s ω=，t ＝20s 时角速度为00.8ωω=，那么飞轮的角加速度β= -0.05 rad/s 2 ，t ＝0到 t ＝100 s 时间飞轮所转过的角度θ= 250rad ． 【解答】飞轮作匀变速转动，据0t ωωβ=+，可得出：200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。

♫定轴转动的转动定律：定轴转动的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如下图．绳与轮之间无相对滑动．假设某时刻滑轮沿逆时针方向转动，那么绳中的力 (A) 处处相等． (B) 左边大于右边． (C) 右边大于左边． (D) 哪边大无法判断． 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1＜m 2)，实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得：21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为m 的重物，飞轮的角加速度为．如果以拉力2mg 代替重物拉绳时，飞轮的角加速度将(A) 小于． (B) 大于，小于2． (C) 大于2． (D) 等于2． 【解答】设飞轮的半径为R ,质量为m ，根据刚体定轴转动定律M J β=，当挂质量为m 的重物是：mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时，有： '2mgR J β=，2'mgRJβ=，比拟二者可得出结论。

理论力学练习册及答案(南华版)

理论力学练习册及答案(南华版)
解：动点取曲柄OA上A点，
动系固连摇杆CB上，定系固连机架。
由速度合成定理 作速度平行四边形。
B点速度为：
由加速度合成定理 作加速度图。
取 方向投影，得：
B点加速度为：
7-4.半径为R的半圆形凸轮以匀速V0沿水平线向右平动，带动顶杆AB沿铅直方向运动，当OA与铅直线夹角为300时，求此时杆AB的速度和加速度。
解：动点取杆OA上A点，动系固连杆O1C上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影，得：
再取动点杆O1C上C点，动系固连套筒B上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影，得：
取 方向投影，得：
第八章 刚体平面运动
分别取节点A、B为研究对象，受力如图
对于节点A： ，
(压)
对于节点B： , (压)
2-11.计算桁架中1、2、3杆的受力。
解：取I-I剖面右边部分为研究对象，受力如图。
,
(拉)
,
(压)
研究节点B: ，
(压)
第三章 空间力系
3-1.图示正立方体，各边长为a，四个力F1、F2、F3、F4大小皆等于F，如图所示，作用的相应的边上。求此力系简化的最终结果，并在图中画出。
8-7.四杆机构中，曲柄OA以匀角速度ω0=25 rad/s绕O轴转动，OA=50 cm，AB=100 cm，O1B= cm。求∠OAB=900时，B点的加速度，摇臂O1B的角速度和角加速度。
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。

《刚体运动习题》课件

《刚体运动习题》课件
详细描述
刚体的转动问题涉及到分析刚体的转动惯量、角速度、角加速度等物理量，以及力和扭矩对刚体转动的影响。通过解决刚体的转动问题，可以了解刚体在转动过程中的运动规律和特点。
刚体的复合运动问题涉及到刚体的平动和转动同时发生的情况。
总结词
刚体的复合运动问题需要综合考虑刚体的平动和转动，分析其相互影响和耦合作用。这类问题通常比较复杂，需要运用力学和运动学的知识进行求解。
总结词
在解答进阶习题时，学生需要具备较强的分析能力和计算能力，能够根据题目要求进行正确的分析和计算，并得出正确的结论。
详细描述
总结词：高难度习题是刚体运动中的高级题目类型，主要考察学生对刚体运动理论的深入理解和应用能力。
感谢您的观看
THANKS
详细描述
刚体的振动问题主要研究刚体在周期性外力作用下的振动现象。
总结词
刚体的振动问题涉及到分析刚体的振动频率、振幅、相位等物理量，以及周期性外力对刚体振动的影响。通过解决刚体的振动问题，可以了解刚体在振动过程中的运动规律和特点，对于工程实践中的振动控制和减振设计具有重要意义。
详细描述
刚体运动的解题方法
03
它基于力学的基本原理和数学工具，如微积分、线性代数和常微分方程等，来推导和求解刚体运动的数学模型。
解析法可以给出精确的解，但有时可能比较复杂，需要较高的数学水平。
解析法是一种通过数学公式和定理来求解刚体运动问题的方法。
几何法是通过图形和几何形状来描述和解决刚体运动问题的方法。
它通过绘制刚体的运动轨迹、速度和加速度等矢量图，以及分析刚体的转动和角速度等来解决问题。
04
建筑结构中的刚体运动是指建筑物在风、地震等外力作用下产生的运动，包括平动、扭转和复合运动等。

理论力学(机械工业出版社)第六章刚体的基本运动习题解答

理论力学(机械工业出版社)第六章刚体的基本运动习题解答

习 题6-1 杆O 1A 与O 2B 长度相等且相互平行，在其上铰接一三角形板ABC ，尺寸如图6-16所示。

图示瞬时，曲柄O 1A 的角速度为rad/s 5=ω，角加速度为2rad/s 2=α,试求三角板上点C 和点D 在该瞬时的速度和加速度。

图6-16m/s 5.051.01=⨯===ωA O v v D C2221n n m/s 5.251.0=⨯===ωA O a a D C 21ττm/s 2.021.0=⨯===αA O a a D C6-2 如图6-17所示的曲柄滑杆机构中，滑杆BC 上有一圆弧形轨道，其半径R =100mm ，圆心O 1在导杆BC 上。

曲柄长OA =100mm ，以等角速度rad/s 4=ω绕O 轴转动。

设t =0时，0=ϕ，求导杆BC 的运动规律以及曲柄与水平线的夹角︒=30ϕ时，导杆BC 的速度和加速度。

图6-17m 4cos 2.04cos 1.02cos 2cos 21t t t R OA x O =⨯⨯===ωϕ m/s 4sin 8.01t xO -= ︒=30ϕ时 m/s 4.01-=O x 21m/s 4cos 2.3t x O -= 21m/s 36.1-=O xm /s 4.0=v 22m/s 771.2m/s 36.1==a6-3 一飞轮绕定轴转动，其角加速度为2ωαc b --=,式中b 、c 均是常数。

设运动开始时飞轮的角速度为0ω，问经过多长时间飞轮停止转动？2ωαc b --= t c b d d 2-=+ωω ⎰⎰-=+t t c b 002d d 0ωωωt bc bc-=00|)arctan(1ωω )arctan(10ωb cbct =6-4 物体绕定轴转动的转动方程为334t t -=ϕ。

试求物体内与转轴相距R =0.5m 的一点，在t =0及t =1s 时的速度和加速度度的大小，并问物体在什么时刻改变其转向。

234t t -=ϕ 294t -=ϕt 18-=ϕ t =0时4=ϕ0=ϕ m/s 245.0=⨯==ωR v 222n m /s 845.0=⨯==ωR a 0τ==αR a2n m/s 8==a a t =1s 时5-=ϕ18-=ϕ m/s 5.255.0=⨯==ωR v222n m /s 5.12)5(5.0=-⨯==ωR a 2τm/s 9)18(5.0-=-⨯==αR a2m/s 4.15=a什么时刻改变其转向0942=-=t ϕs 32=t6-5 电机转子的角加速度与时间t 成正比，当t =0时，初角速度等于零。

刚体的转动部分习题分析与解答

刚体的转动部分习题分析与解答

动轨迹为一个圆弧。
刚体的定轴转动和平面转动的比较
03
定轴转动和平面转动是刚体转动的两种基本形式，它们在运动
学和动力学上有一些不同之处，如角速度、角加速度等。
03
刚体的动能与势能
刚体的动能
总结词
刚体的动能是指刚体在转动过程中所 具有的能量，与刚体的转动速度和质 量分布有关。
详细描述
刚体的动能计算公式为$E_{k} = frac{1}{2}Iomega^{2}$，其中$I$为刚体的转 动惯量，$omega$为刚体的角速度。转动惯量 是描述刚体质量分布对其转动影响的物理量， 与刚体的质量分布、形状和大小有关。
解答过程
钢球下落过程中，其速度逐渐增大，故其动能在 不断增加。同时，钢球离地面的高度逐渐减小， 故其势能在不断减小。由于钢球下落过程中只有 重力做功，故其机械能守恒。
习题五：关于刚体的机械能守恒的题目
总结词
理解机械能守恒的概念，掌握机械能守恒的条件和机械能守恒的计算方法。
详细描述
机械能守恒是指系统内各种形式的能量在相互转化时总量保持不变。对于刚体系统，只有重力或弹力 做功时机械能守恒。机械能
刚体的势能
总结词
刚体的势能是指刚体在转动过程中相对于某一参考点所具有 的能量。
详细描述
刚体的势能计算公式为$U = -GMmcostheta$，其中$G$为万 有引力常数，$M$和$m$分别为两个质点的质量，$theta$为 两质点连线和垂直于势能参考平面的夹角。对于刚体，势能的 具体值取决于参考点的选择。
实际问题。
习题五解答与解析
要点一
总结词
刚体的角动量守恒
要点二
详细描述
这道题目考察了学生在刚体转动中如何应用角动量守恒的 知识。学生需要理解角动量的概念，知道角动量等于刚体 的转动惯量乘以角速度，并能够根据角动量守恒的条件判 断刚体的运动状态。

大学物理刚体的转动知识点及试题带答案

大学物理刚体的转动知识点及试题带答案

刚体的转动一、基本要求：1、理解刚体的概念；了解刚体的平动和转动；掌握转动惯量的物理意义；掌握力矩的物理意义及其计算。

2、理解转动惯量的物理意义及其计算；掌握刚体定轴转动的转动定律及计算。

3、理解质点和刚体的角动量；掌握角动量守恒定律的适用条件及应用；掌握刚体转动动能的概念及计算。

二、主要内容： 1、刚体：是在外力作用下形状和大小保持不变的物体称为刚体。

是一个理想化的力学模型，它是指各部分的相对位置在运动中（无论有无外力作用）均保持不变的物体。

即运动过程中没有形变的物体。

2、平动：当刚体中所有点的运动轨迹都保持完全相同时，或者说刚体内任意两点间的连线总是平行于它们的初始位置间的连线时，刚体的运动叫作平动。

3．转动：刚体中所有的点都绕同一条直线作圆周运动，这种运动称为转动。

这条直线叫作转轴。

4、描述刚体转动的物理量引入：刚体作定轴转动时，刚体上的各点都绕定轴作圆周运动。

刚体上各点的速度和加速度都是不同的，用线量描述不太方便。

但是由于刚体上各个质点之间的相对位置不变，因而绕定轴转动的刚体上所有点在同一时间内都具有相同的角位移，在同一时刻都具有相同的角速度和角加速度，故采用角量描述比较方便。

为此引入角量：角位置、角位移、角速度、角加速度。

5、角量与线量的关系半径R ，角位移θ∆ 弧长 θ∆⋅=∆R s 线速度v: ωθR t R t s v t t =∆∆=∆∆=→∆→∆lim lim法向加速度： 222)(ωωr RR R v a n === 切向加速度： αωωτ⋅=⋅===R dtd R R dt d dt dv a )( 结论：刚体作定轴转动时，在某一时刻刚体上所有各点的角位移、角速度和角加速度都是相同的；而各点的线位移、线速度和线加速度均与r 成正比。

6转动定律：刚体在合外力矩的作用下，刚体所获得的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比。

● 合外力矩和转动惯量都是相对于同一转轴而言的； ● 转动定律是解决刚体定轴转动的基本定律，它的地位与质点动力学中牛顿第二定律相当。

工程力学6第六章

工程力学6第六章

点的曲线运动与刚体的定轴转动的比较 运动性质 匀速运动 点的曲线运动 刚体定轴转动
s s0 vtv为常量 0 t 为常量
v v0 a t
0 at
1 2 0 0t t 2
匀变速 运动
2 2 v 2 v0 2a s s0 2 0 2 0
• 例6-2 • 作业：导学篇P88 1、6、7
按自然法 ds d s R , v R R dt dt dv d a R R dt dt v2 an R 2 R
M点全加速度
2 a a2 an R 2 4
tan
a an


2
例：已知轮1的角速度和角加速度，轮2的角速度与 角加速度？

则角速度为 d lim f `t t 0 t dt 即刚体绕定轴转动的角速度等于 转角对时间的一阶导数, 单位：rad / s
3.角加速度
角加速度是反映角速度变化快慢的物理量 如右图所示刚体， 设在瞬时t， 刚体的角速度为 到瞬时t t角速度变为 刚经过t时间后， 角速度的改变量为
• 二、以矢积表示转动刚体上点的速度与加速度 • 如图6-7
M点的速度 v r , 三者按右手法则确定方向。 矢积的 r 大小 : r r sin R v M点的加速度 dv d dr a r r v dt dt dt r ( r ) a a n 矢积 r 的大小： r r sin R a 矢积 v 的大小： v v sin 90 R 2
如何确定刚体在空间的位置?

理论力学6刚体的基本运动

理论力学6刚体的基本运动

当刚体作平动时，只须给出刚体内任意一点的运动，就可以 完全确定整个刚体的运动。这样，刚体平动问题就可看为点 的运动问题来处理。 这样，刚体平动问题就可看为点的运动问题来处理。
综上所述，可以得出刚体平动的特点： 1、平动刚体上的各点具有形状相同的运动轨迹。 2、平动刚体上的各点在某一瞬时具有相同的速度和加速度。 3、刚体平动时的运动分析可以简化为其上任意一点(一般取为 质心)的运动分析。������ ������
因此，研究刚体的平动，可以归结为研究刚体内任一点的运 动。
6.1 刚体的平行移动
平动刚体上各点的速度
平动刚体上各点的加速度
6.1 刚体的平行移动
注意：平动刚体内的点，不一定沿直线运动，也不一定保持 在平面内运动，它的轨迹可以是任意的空间曲线。 如果平动刚体内各点的轨迹都是平面曲线或直线，则这些特 殊情形称为平面平动或直线平动。 由上述定理可见：
即：定轴转动刚体内任一点的速度, 等于该点的转动半径与刚体角速度 的乘积。 式中v与ω两者正负相同。故速度是沿着点M的轨迹圆周的切 线，指向转动前进的一方。
6.3 转动刚体内各点的速度和加速度
即：转动刚体内任一点速度的大小等于刚体角速度与该点到轴 线的垂直距离的乘积，它的方向沿圆周的切线而指向转动的一 方。
6.1 刚体的平行移动
平动的实例
夹 板 锤 的 锤 头
6.1 刚体的平行移动
2. 平动的特点
定理：当刚体作平动时，刚体内所有各点的轨迹形状完 全相同，而且在每一瞬时，刚体各点的速度相等，各点 的加速度也相等。 证明：
rA rB BA
◆速度 刚体平动时，刚体内任一线段AB 的长度和方向都保持不变。 因而 x
6.1 刚体的平行移动

第6章刚体的平面运动习题解答080814.

第6章刚体的平面运动习题解答080814.

第六章 刚体的平面运动本章要点一、刚体平面运动的描述1 刚体的平面运动方程：)(t x x A A =，)(t y y A A =，)(t ϕϕ=.2 平面图形的运动可以看成是刚体平移和转动的合成运动：刚体的平面运动（绝对运动）便可分解为随动坐标系（基点）的平移（牵连运动）和相对动坐标系（基点）的转动（相对运动）。

其平移部分与基点的选取有关，而转动部分与基点的选取无关。

因此，以后凡涉及到平面图形相对转动的角速度和角加速度时，不必指明基点，而只说是平面图形的角速度和角加速度即可。

二、平面运动刚体上点的速度1 基点法：平面图形内任一点B 的速度，等于基点A 的速度与B 点绕基点转动速度的矢量和，即BA A B v v v +=，其中BA v 的大小为ωAB v BA =，方向垂直于AB ，指向与图形的转动方向相一致。

2投影法速度投影定理：在任一瞬时，平面图形上任意两点的速度在这两点连线上的投影相等，即AB A AB B v v ][][=3瞬心法任意瞬时平面运动图形上都存在速度为零的点，称为该平面图形的瞬时速度中心，简称瞬心。

平面图形上各点速度在某瞬时绕瞬心的分布与绕定轴转动时的分布相同，但有本质区别。

绕定轴转动时，转动中心是一个固定不动的点，而速度瞬心的位置是随时间而变化的。

面图形内任意一点的速度，其大小等于该点到速度瞬心的距离乘以图形的角速度，即ωCM v M =，其方向与CM 相垂直并指向图形转动的一方。

若在某瞬时，0=ω，则称此时刚体作瞬时平移，瞬时平移刚体的角加速度不为零。

解题要领：1 建立平面运动刚体的运动方程时要注意选取合适的点为基点，以使问题简单，。

2 由于在基点建立的是平移坐标系，因此，相对基点的角速度就是相对惯性坐标系的角速度。

3 平面运动刚体上点的速度计算的3种方法各有所长：基点法包含刚体运动的速度信息，但过程繁杂；速度投影法能快捷地求出一点的速度，但失去角速度信息；瞬心法简单明了和直观是常用的方法。

理论力学运动学习题及详解

理论力学运动学习题及详解

y f 2 (t ) z f 3 (t )
2 2
a x x a y y a z z
2 2 2
v vx v y vz
2
a ax a y az
方向均由相应的方向余弦确定。
第2章 运动学练习
二．基本公式 自然法（轨迹已知时）
运动方程 速度

ae 5 2 0 r 4
5 2a r0 4
B
aC 0
O2
3销钉C固定在AB杆，在滑槽O2D中运动，该瞬时O1A与AB水平，O2D
铅直，且O1A=AC=CB=O2C=r，ω0=常数,求
AB、O2 D、 AB、O2 D .
D
n aCA
（2）加速度分析
AB 0
a 常量， an 0
，点做何种运动（ B）。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ，其轨迹方程为(
B)
A.3x 4 y 36 0, C.2 x 2 y 24 0,
第2章 运动学练习
B.3x 2 y 18 0 D.2 x 4 y 36 0
1.选择题：
【练习题】
(4). 如图所示平面机构中，O1A=O2B= r, O1O2 =AB, O1A以匀角速度绕垂直于图 面的O1轴转动，图示瞬时，C点的速度为：( D )
A.
B. C.
Vc 0
Vc r a
2 2
水平向右
O1 A
O2
Vc r0 D. Vc r0
铅直向上 水平向右
2.刚体运动学
基本运动 平面运动

理论力学8刚体的基本运动

理论力学8刚体的基本运动

前面都为数量表达式，只有大小，而未标明方向； 矢量表达既有大小，又有方向。
一. 角速度和角加速度的矢量表示
按右手定则规定
w ， 的方向。
大小:|w ||ddt |
dw dw k k
dt dt
方向如图 w wk
15
二 刚体内任一点的线速度和线加速度的矢积表示
vRw rsin w |w r|wrsin Rw
小于90o , 在同一瞬间的速度和加速度的分布图为:
各点速度分布图
各点加速度分布图
10
§8-4 绕定轴转动刚体的传动问题
传动比：通常称主动轮与从动轮角速度之比
i12
w1 w2
一.齿轮传动
因为是做纯滚动(即没有相对滑动) 1.内啮合
vF vE vF vE
wF rF wE rE
定义齿轮传动比
iEF
aC n Rw02 0.532 4.5m/s 2
aC (aC )2 (aC n )2 12 4.52 4.61 m/s2
tg
aC aC n
1 4.5
0.222,
12.5
⑤ t=3s 时， aC aA 1m/s2,aCn Rw 2 0.592 40.5m/s2
aC
12 40.52 40.51m/s2,
w 2 w02 2
7
§8-3 转动刚体内各点的速度和加速度
一. 线速度V和角速度w之间的关系(即角量与线量的关系)
w , 对整个刚体而言(各点都一样)；
v, a 对刚体中某个点而言(各点不一样)。
v

v
lim
t0
R t
wR
v wR
8
二.角加速度 与an ,a 的关系

《理论力学》第六章 刚体的基本运动习题全解

《理论力学》第六章 刚体的基本运动习题全解

第六章 刚体的基本运动 习题全解[习题6-1] 物体绕定轴转动的运动方程为334t t -=ϕ（ϕ以rad 计，t 以s 计）。

试求物体内与转动轴相距m r 5.0=的一点，在00=t 与s t 11=时的速度和加速度的大小，并问物体在什么时刻改变它的转向？ 解：角速度： 2394)34(t t t dt ddt d -=-==ϕω 角加速度：t t dtddt d 18)94(2-=-==ωα速度： )94(2t r r v -==ω)/(2)094(5.0|20s m r v t =⨯-⨯===ω)/(5.2)194(5.0|21s m v t -=⨯-⨯==切向加速度：rt t r a t 18)18(-=-==ρα法向加速度：22222)94()]94([t r rt r v a n -=-==ρ 加速度： 422222222)94(324])94([)18(t t r t r rt n a a n t -+=-+-=+=)/(8165.0)094(0324|24220s m r a t =⨯=⨯-+⨯== )/(405.1581.305.0)194(1324|24221s m r a t =⨯=⨯-+⨯== 物体改变方向时，速度等于零。

即：0)94(2=-=t r v )(667.0)(32s s t ==[习题6-2] 飞轮边缘上一点Ｍ，以匀速ｖ＝１０ｍ／ｓ运动。

后因刹车，该点以)/(1.02s m t a t =作减速运动。

设轮半径Ｒ＝０.４ｍ，求Ｍ点在减速运动过程中的运动方程及ｔ＝２ｓ时的速度、切向加速度与法向加速度。

解：t dtd a t 1.04.022-===ϕρα （作减速运动，角加速度为负）t dt d 25.022-=ϕ12125.0C t dtd +-=ϕ2130417.0C t C t ++-=ϕ12124.005.0)125.0(4.0C t C t dtd R v +-=+-⨯==ϕ104.0005.0|120=+⨯-==C v t图题46-251=C0000417.0|2130=+⨯+⨯-==C C t ϕ 02=C ，故运动方程为： t t 250417.03+=ϕt t t t R s 100167.0)250417.0(4.033+-=+-==ϕ速度方程：1005.02+-=t v)/(8.910205.0|22s m v t =+⨯-== 切向加速度：)/(2.021.01.0|22s m t a t t -=⨯-=-== 法向加速度：222)25125.0(4.0+-⨯==t a n ρω)/(1.240)252125.0(4.0|2222s m a t n =+⨯-⨯==[习题6-3] 当起动陀螺罗盘时，其转子的角加速度从零开始与时间成正比地增大。

第六章刚体的基本运动习题解答

第六章刚体的基本运动习题解答

习 题6-1 杆O 1A 与O 2B 长度相等且相互平行，在其上铰接一三角形板ABC ，尺寸如图6-16所示。

图示瞬时，曲柄O 1A 的角速度为rad/s 5=ω，角加速度为2rad/s 2=α,试求三角板上点C 和点D 在该瞬时的速度和加速度。

图6-16m/s 5.051.01=⨯===ωA O v v D C2221n n m/s 5.251.0=⨯===ωA O a a D C21ττm/s 2.021.0=⨯===αA O a a D C6-2 如图6-17所示的曲柄滑杆机构中，滑杆BC 上有一圆弧形轨道，其半径R =100mm ，圆心O 1在导杆BC 上。

曲柄长OA =100mm ，以等角速度rad/s 4=ω绕O 轴转动。

设t =0时，0=ϕ，求导杆BC 的运动规律以及曲柄与水平线的夹角︒=30ϕ时，导杆BC 的速度和加速度。

图6-17m 4cos 2.04cos 1.02cos 2cos 21t t t R OA x O =⨯⨯===ωϕ m/s 4sin 8.01t xO -= ︒=30ϕ时 m /s 4.01-=O x 21m/s 4cos 2.3t x O -= 21m /s 36.1-=O xm /s 4.0=v 22m /s 771.2m /s 36.1==a6-3 一飞轮绕定轴转动，其角加速度为2ωαc b --=,式中b 、c 均是常数。

设运动开始时飞轮的角速度为0ω，问经过多长时间飞轮停止转动？2ωαc b --=t c b d d 2-=+ωω ⎰⎰-=+tt c b 02d d 0ωωωt bc bc -=0|)arctan(1ωω)arctan(10ωbc bct =6-4 物体绕定轴转动的转动方程为334t t -=ϕ。

试求物体内与转轴相距R =0.5m 的一点，在t =0及t =1s 时的速度和加速度度的大小，并问物体在什么时刻改变其转向。

234t t -=ϕ 294t -=ϕt 18-=ϕ t =0时4=ϕ0=ϕ m/s 245.0=⨯==ωR v222n m/s 845.0=⨯==ωR a0τ==αR a2n m /s 8==a a t =1s 时5-=ϕ18-=ϕ m/s 5.255.0=⨯==ωR v222n m/s 5.12)5(5.0=-⨯==ωR a2τm/s 9)18(5.0-=-⨯==αR a2m/s 4.15=a 什么时刻改变其转向 0942=-=t ϕs 32=t6-5 电机转子的角加速度与时间t 成正比，当t =0时，初角速度等于零。

06 刚体的基本运动

06 刚体的基本运动

3 1 ln 3 1 3 0 t
6.4 已知轮 I、II、III 的半径分别为 r1＝30cm，r2＝75cm，r3＝40cm，轮 I 的转速 n1＝ 100rpm。求物块 M 的上升速度，胶带 AB、BC、CD、DA 各段上点的加速度的大 小。 B A
r3
r2
n1
O1 DБайду номын сангаас
r1
2
O2
1
C
v
I
当 d＝r=5cm 时，
II
50 50 2 2 (rad/s2) 2 r 5 2n I II 20 (rad/s) 60
所以，当 d＝r 时，轮 II 边缘上的一点的全加速度的大小
2 4 a R II II 15 (2 )2 (20 )4 59218 (cm/ s2 )
a A a
n n aM aA a 2 ,
M 点：∵AB 杆作曲线平动，∴ vM v A a , 6.3
a M a A a
如图所示，一飞轮绕固定轴 O 转动，其轮缘上任一点 M 的全加速度在某运动 过程中与轮半径的交角恒为 60o。当运动开始时，其转角 0 0 ，角速度为0。求 飞轮的转动方程以及角速度与转角的关系。
M
解：
1
n1
30
， 2
1 r1
r2
AB 和 CD 之间各点作匀速直线运动， AD 和 BC 之间各点作匀速圆周运动，所以
a AD r112 32.9 (cm/s2)
2 a BC r2 2 13.16 (cm/s2)
aAB aCD 0 ， 物块 M 的上升速度 v M r3 2 1.676 (cm/s)

刚体习题及答案知识讲解

刚体习题及答案知识讲解
➢ 撞击前后系统的动量是否守恒？为什么？ ➢ 动能是否守恒？为什么？ ➢ 角动量是否守恒？为什么？ （2）子弹和轮开始一起运动时，
轮的角速度是多少？
θ A v0 cos
v0 sin
R
例6.一块质量为M＝1kg 的木板，高L＝0.6m，可以其一边为轴自 由转动。最初板自由下垂.今有一质量m＝10g的子弹，垂直击中 木板A点，l＝0.36m，子弹击中前速度为500m/s，穿出后的速度 为200m/s， 求： (1) 子弹给予木板的冲量
解法一： 用转动定律求解
在恒力矩和摩擦力矩作用下，0—10s内有：
M M r J1
1 1t1
M
Mr
J
ω1 t1
移去恒力矩后，0—90s内有：
Mr J2
0 1 2t2
Mr
J
2
t2
J Mt1t2
1(t1 t2 )
54kg m2
解题过程尽可能用文字式，最后再带入数字。
解法二:
0-10s: 0-90s:
m 的匀质圆盘，此圆盘具有光滑水平轴，然后在下端系一质量也 为 m的物体，如图。求当物体由静止下落h 时的速度v。
例11.如图所示，一均匀细杆长为 l ，质量为 m，平放在摩擦系数
为μ的水平桌面上，设开始时杆以角速度 ω0 绕过中心 o 且垂直于
桌面的轴转动，试求:
0
（1）作用在杆上的摩擦力矩;
（2）经过多长时间杆才会停止转动。
人 : Mg T 2 Ma
物:
1
1
T1 - 2 Mg = 2 Ma
轮： (T2 T1)R J
a R
2 a 7g
o
T2
T1
A Ba
Mg 1

理论力学习题解答(第六章)

理论力学习题解答(第六章)

6－1在图示四连杆机构中，已知：匀角速度O ω，OA =B O 1=r 。

试求在°=45ϕ且AB ⊥B O 1的图示瞬时，连杆AB 的角速度AB ω及B 点的速度。

解：连杆AB 作平面运动，由基点法得BA A B v v v +=由速度合成的矢量关系，知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv （逆时针）B 点的速度2245/r cos v O A B ω=°=v （方向沿AB ）6－2. 在图示四连杆机构中，已知：3.021===L B O OA m ，匀角速度2=ωrad/s 。

在图示瞬时，11==L OB m ，且杆OA 铅直、B O 1水平。

试求该瞬时杆B O 1的角速度和角加速度。

解：一．求1ω60230..OA v A =×=⋅=ω m/s取A 为基点，则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+×==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针 二．求1ε取点A 为基点，则有n BA A a a a a a ++=+ττBA nB B将上式向X 轴投影21222857s /m .B O /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅−=++−=−=+−ϕϕωϕϕϕϕϕττ杆B O 1的角加速度7.1923.0/8.57/11===B O a B τεrad/s 2逆时针6－3.图示机构中，已知：OA =0.1m ， DE =0.1m ，m 31.0=EF ，D 距OB 线为h=0.1m ；rad 4=OA ω。

大学物理习题参考解答物理习题参考解答刚体基本运动_转动定律_动能定理

大学物理习题参考解答物理习题参考解答刚体基本运动_转动定律_动能定理

选择题_03图示单元四 刚体基本运动 转动动能 1一 选择题01. 一刚体以每分钟60转绕z 轴做匀速转动(ω沿转轴正方向)。

设某时刻刚体上点P 的位置矢量为345r i j k =++，单位210m -，以210/m s -为速度单位，则该时刻P 点的速度为： 【 B 】(A) 94.2125.6157.0v i j k =++；(B) 25.118.8v i j =-+；(C) 25.118.8v i j =--；(D) 31.4v k =。

02. 轮圈半径为R ，其质量M 均匀布在轮缘上，长为R ，质量为m 的均质辐条固定在轮心和轮缘间，辐条共有2N 根。

今若将辐条数减少N 根但保持轮对通过轮心，垂直于轮平面轴的转动惯量保持不变，则轮圈的质量为 【 D 】(A)12N m M +； (B) 6N m M +； (C) 23N m M +； (D) 3Nm M +。

03. 如图所示，一质量为m 的均质杆长为l ，绕铅直轴OO '成θ角转动，其转动惯量为 【 C 】(A)2112ml ；(B) 221sin 4ml θ；(C) 221sin 3ml θ； (D) 213ml 。

04. 关于刚体对轴的转动惯量，下列说法中正确的是 【 C 】 (A) 只取决于刚体的质量,与质量的空间分布和轴的位置无关； (B) 取决于刚体的质量和质量的空间分布，与轴的位置无关； (C) 取决于刚体的质量、质量的空间分布和轴的位置；(D) 只取决于转轴的位置，与刚体的质量和质量的空间分布无关。

05. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ，若A B ρρ>，但两圆盘的质量与厚度相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为A J 和B J ，则 【 B 】(A) A B J J >； (B) B A J J >；(C) A B J J =； (D) A J 和B J 哪个大，不能确定。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章刚体的基本运动习题解答习题6-1 杆O 1A 与O 2B 长度相等且相互平行，在其上铰接一三角形板ABC ，尺寸如图6-16所示。

图示瞬时，曲柄O 1A 的角速度为ω=5rad/s，角加速度为α=2rad/s2, 试求三角板上点C 和点D 在该瞬时的速度和加速度。

图6-16v C =v D =O 1A ω=0. 1⨯5=0. 5m/sa C =a D =O 1A ωττn n 2=0. 1⨯5=2. 5m/s222a C =a D =O 1A α=0. 1⨯2=0. 2m/s6-2 如图6-17所示的曲柄滑杆机构中，滑杆BC 上有一圆弧形轨道，其半径R=100mm，圆心O 1在导杆BC 上。

曲柄长OA =100mm，以等角速度ω=4rad/s绕O 轴转动。

设t =0时，求导杆BC 的运动规律以及曲柄与水平线的夹角ϕ=30︒时，导杆BC 的速度和加速度。

ϕ=0，图6-17x O 1=2OA cos ϕ=2R cos ωt =2⨯0. 1⨯cos 4t =0. 2cos 4t m O 1=-0. 8sin 4tm/s ϕ=30︒时 x O 1=-0. 4m / s xO 1=-3. 2cos 4t m/s2 O 1=-1. 63m /s 2 x xv =0. 4m /s a =1. 63m /s 2=2. 771m /s 26-3 一飞轮绕定轴转动，其角加速度为α=-b -c ω2, 式中b 、c 均是常数。

设运动开始时飞轮的角速度为ω0，问经过多长时间飞轮停止转动？α=-b -c ω2d ωb +c ω2=-d t ⎰d ωb +c ω2ω0=⎰t-d tarctan(1bcc bω) |ω=-tarctan(c bω0)6-4 物体绕定轴转动的转动方程为ϕ=4t -3t 3。

试求物体内与转轴相距R =0.5m的一点，在t =0及t =1s时的速度和加速度度的大小，并问物体在什么时刻改变其转向。

2=4-9t 2 ϕ =-18t ϕ=4t -3t ϕt =0时=4 ϕ =0 ϕv =R ω=0. 5⨯4=2m/s2=0. 5⨯4=8m/s222a τ=R α=0a =a n =8m /s t =1s时=-5 ϕ =-18 ϕv =R ω=0. 5⨯5=2. 5m/sa n =R ω2=0. 5⨯(-5) =12. 5m/s222a τ=R α=0. 5⨯(-18) =-9m/sa =15. 4m/s 什么时刻改变其转向 =4-9t 2=0 t = ϕ23s26-5 电机转子的角加速度与时间t 成正比，当t =0时，初角速度等于零。

经过3s 后，转子转过6圈。

试写出转子的转动方程，并求t =2s时转子的角速度。

α=ct d ω=ct d t d ϕ=1ct ϕ=2⎰ωd ω=⎰tct d t ω=12ct21d t 26t =3s时，ϕ=6⨯2π=12π 12π=ct312794π3ϕ=t =1. 396t 3916c =612π⨯c ⨯3 =4π3t =2s时ω=6-6 杆OA 可绕定轴O 转动。

一绳跨过定滑轮B ，其一端系于杆OA 上A 点，另一端以匀速u 向下拉动，如图6-18所示。

设OA=OB=l ，初始时ϕ=0，试求杆OA 的转动方程。

AB =2l -ut4π3t2=4π3⨯4=16π3=16. 76r a d /scos ∠OAB =即 cosAB /2OA =1-ut 2l=2l -ut 2l=1-ut 2lϕ2ϕ=2arccos(1-ut 2l)6-7 圆盘绕定轴O 转动。

在某一瞬时，轮缘上点A 的速度为v A =0. 8m/s，转动半径为盘上任一点B 的全加速度a B 与其转动半径OB 成θ角，且tan θ=0. 6，如图6-19r A =0. 1m ；所示。

试求该瞬时圆盘的角加速度。

v A r Av A =r A ω=0. 8m/s ω=tan θ=图6-190. 8==8r a d / s 0. 12αω2=0. 6 |α|=0. 6⨯ω=38. 4r a d /s26-8 如图6-20所示，电动机轴上的小齿轮A 驱动连接在提升铰盘上的齿轮B ，物块M 从其静止位置被提升，以匀加速度升高到1.2m 时获得速度0.9m/s。

试求当物块经过该位置时：（1）绳子上与鼓轮相接触的一点C 的加速度；（2）小齿轮A 的角速度的角加速度。

图6-20(1)0. 9-0=2a τ⨯1. 2 a τ=220. 492. 4=0. 3375ωB =a n =ωA ωB=0. 90. 6=1. 5 a n =0. 6⨯1. 52=1. 3520. 3375R B R A a τR C==+1. 352=1. 39m/s2450150=3 ωA =3ωB =4. 5r a d / s=0. 5625 αA =3αB =1. 6875r a d /s2αB =0. 33750. 66-9 杆OA 的长度为l , 可绕轴O 转动，杆的A 端靠在物块B 的侧面上，如图6-21所示。

若物块B 以匀速v 0向右平动，且x =v 0t , 试求杆OA 的角速度和角加速度以及杆端A 点的速度。

图6-21x =v 0t cos ϕ=x lv 0t lϕ=a r c c 0 lv tv 0=ωO =ϕl -(v 0t l )2=lv 0222-v tO =αO =ω v 0t (l23223-v t )v A =l ωO =lv 0l -v t22206-10 图6-22所示机构中，杆AB 以匀速v 向上滑动，通过滑块A 带动摇杆OC 绕O 轴作定轴转动。

开始时ϕ=0，试求当ϕ=π/4时，摇杆OC 的角速度和角加速度。

图6-22tan ϕ=vt lv l v对时间求导sec ϕ=ϕ2=v l2cos ϕ=ω=ϕl sec ϕ2= α=ωv l⨯(-s i n 2ϕ) ω=-v l222s i n 2ϕc o s ϕϕ=π/4时ω=v 2lα=-v 2l226-11 如图6-23所示，电动绞车由皮带轮Ⅰ和Ⅱ以及鼓轮组成，鼓轮Ⅲ和皮带轮Ⅱ刚性地固定在同一轴上。

各轮的半径分别为r 1=0. 3m ，r 2=0. 75m ，r 3=0. 4m ，轮Ⅰ的转速为n 1=100r/min。

设皮带轮与皮带之间无相对滑动，求重物M 上升的速度和皮带各段上点的加速度。

图6-23ω1=πn 130r 1=10π30. 3⨯10π3=4π3ω2=r 2ω1=0. 75v =r 3ω2=0. 4⨯a AB =a CD =04π3=1. 6755m/sa AD =r 1ω=0. 3⨯(2110π3) =210π32=32. 8987m/s2a BC =r 2ω=0. 75⨯(224π3) =24π322=13. 1595m/s6-12 两轮Ⅰ、Ⅱ铰接于杆AB 的两端，半径分别为r 1=150mm ，r 2=200mm ，可在半径为R =450mm的曲面上运动，在图6-24所示瞬时，点A 的加速度大小为a A=1200mm/s2，方向与OA 连线成60︒角。

试求该瞬时：（1）AB 杆的角速度和角加速度；（2）点B 的加速度。

图6-24a A =1200mm/sanA2=a A cos 60︒=600mm/s 2=v A R +r 122=(R +r 1) ωω=600450+150=1rad/sa A =a A sin 60︒=600τ3=(R +r 1) αα=6003R +r 1=23rad/sa B =(R +r 2) ωτn2=650mm/s2a B =(R +r 2) α=650a B =1300mm/s23mm/s26-13 如图6-25所示，机构中齿轮Ⅰ紧固在杆AC 上，AB=O1O 2，齿轮Ⅰ与半径为r 2的齿轮Ⅱ啮合，齿轮Ⅱ可绕O 2轴转动且与曲柄O 2B 没有联系。

设O 1A = O2B=l ，ϕ=b sin ωt ，试确定t=π(2ω) 时，轮Ⅱ的角速度的角加速度。

图6-25ωO 当t =π2B=b ωc o s =-b ω=ϕωt αO B =ϕ22s i n ωtωO2B2ω=0 v B =02=-b ω a B =l αO 2B =-bl ω a D =a B =-bl ω时v D =v B =0(齿轮Ⅰ与杆AC 平动，点D 为轮I 、II 接触点) ωII =0αOτ2ττ22BαII =a D r 2τ=-bl ωr 226-14 如图6-26所示，摩擦传动机构的主动轴Ⅰ的转速为n =600r/min。

轴Ⅰ的轮盘与轴Ⅱ的轮盘接触，接触点按箭头A 所示的方向移动。

距离d 的变化规律为d =100-5t ，其中d 以mm 计，t 以s 计。

已知r=50mm，R =150mm。

求：（1）以距离d 表示的轴Ⅱ的角加速度；（2）当d =r 时，轮B 边缘上一点的全加速度。

图6-26(1)ω=πn 301000πd =20πω2=1000π 1000π5000π2d =-⨯(-5) =rad/s 222d d d2=-α2=ω(2) d =r 时ω2=1000π504=20π2α2=2πrad/sa B =R ω2+α2=1502(20π)+4π42=300π40000π+1=592. 177⨯10mm/s232=592. 177m/s26-15 如图6-27所示，录音机磁带厚为δ，图示瞬时两轮半径分别为r 1和r 2，若驱动轮Ⅰ以不变的角速度ω1转动，试求轮Ⅱ在图示瞬时的角速度和角加速度。

图6-27r 1ω1=r 2ω2 ω2=r 1r 2ω1 1ω1-r 2ω2rr 22= 2 ω 1ω1=r 2ω2+r 2ωrδ2πd ϕ1轮Ⅰ转过一周(2π)，半径增大δ，转过d ϕ1，则增大故 d r 1= d r 1d t 1=rδ2πd ϕ1=δ2π⨯d ϕ1d tδ2πω1r 1r 22=-δ，故r而在轮Ⅰ转过一周(2π)时，轮Ⅱ半径减小2=α2=ω1ω1-r 2ω2rr 2δ2π⨯r 1r 2⨯ω11ω1-r 2⨯r =r 1r 2ω1=1r 2-r 1r 2r r ⨯22ω1δ=2πω1⨯r 2+r 1⨯ 2δ2πr 1r 2ω1ω1r22r 2(1+r 1=r2) 2r 2⨯δ2πω2122=ω1δ2πr (1+ r 1)2r22。