第6章刚体的基本运动
- 格式：doc
- 大小：497.50 KB
- 文档页数：12
下载文档原格式
合集下载
理论力学第七版
equilibrium)
公理3 (Axiom 3) 加减平衡力系原理(The Principle of Addition or 公理
Subtraction Equilibrium Forces System)
推理1 推理 (Inference 1) 力的可传性(The Principle of Transmissibility) 推理2 推理 (Inference 2) 三力平衡汇交定理(Theorem of Three-force
被约束体
轴可在孔内任意转动， 轴可在孔内任意转动， 也可沿孔的中心线移动， 也可沿孔的中心线移动，但 轴承阻碍轴沿孔径向向外的 约束 位移。 位移。
第一章 静力学公理和物体的受力分析
1－2 约束和约束力 －
1-2 Constraints and Reactions of Constraints 反力方向 过接触点，沿接触面公法线指向轴心。 过接触点，沿接触面公法线指向轴心。 由于轴在孔内可任意转动， 由于轴在孔内可任意转动，故而轴 与孔的接触点位置是不定的。 与孔的接触点位置是不定的。因此反力 的方向一般预先不能确定。 的方向一般预先不能确定。但这样的一 个反力常用两个过轴心的， 个反力常用两个过轴心的，大小未知的 正交分力F 来表示。 正交分力 AX、FAY来表示。此二力指向 可任意假定。 可任意假定。
1－2 约束和约束力 － 约束和约束力(Constraints and Reactions of Constraints)
约束特点 阻碍物体沿接触面法线，并指向约束的运动。 作用点 接触点 反力方向 过接触点，沿接触面公法线，指向被约束物体
第一章 静力学公理和物体的受力分析
1－2 约束和约束力 － 约束和约束力(Constraints and Reactions of Constraints)
公理3 (Axiom 3) 加减平衡力系原理(The Principle of Addition or 公理
Subtraction Equilibrium Forces System)
推理1 推理 (Inference 1) 力的可传性(The Principle of Transmissibility) 推理2 推理 (Inference 2) 三力平衡汇交定理(Theorem of Three-force
被约束体
轴可在孔内任意转动， 轴可在孔内任意转动， 也可沿孔的中心线移动， 也可沿孔的中心线移动，但 轴承阻碍轴沿孔径向向外的 约束 位移。 位移。
第一章 静力学公理和物体的受力分析
1－2 约束和约束力 －
1-2 Constraints and Reactions of Constraints 反力方向 过接触点，沿接触面公法线指向轴心。 过接触点，沿接触面公法线指向轴心。 由于轴在孔内可任意转动， 由于轴在孔内可任意转动，故而轴 与孔的接触点位置是不定的。 与孔的接触点位置是不定的。因此反力 的方向一般预先不能确定。 的方向一般预先不能确定。但这样的一 个反力常用两个过轴心的， 个反力常用两个过轴心的，大小未知的 正交分力F 来表示。 正交分力 AX、FAY来表示。此二力指向 可任意假定。 可任意假定。
1－2 约束和约束力 － 约束和约束力(Constraints and Reactions of Constraints)
约束特点 阻碍物体沿接触面法线，并指向约束的运动。 作用点 接触点 反力方向 过接触点，沿接触面公法线，指向被约束物体
第一章 静力学公理和物体的受力分析
1－2 约束和约束力 － 约束和约束力(Constraints and Reactions of Constraints)
刚体运动学的基本原理与公式
刚体运动学的基本原理与公式引言刚体运动学是物理学中一个重要的分支，研究物体在空间中的运动规律。
通过分析刚体的运动，我们可以揭示物体在空间中的位置、速度和加速度等关键信息。
本文将介绍刚体运动学的基本原理和公式，帮助读者更好地理解和应用这一领域的知识。
一、刚体的定义与特性刚体是指在运动过程中形状和大小不发生变化的物体。
与之相对，我们称之为非刚体的物体在运动过程中可能发生形变。
刚体的特性包括质量、形状、大小和位置等。
在刚体运动学中，我们主要关注刚体的位置、速度和加速度等运动参数。
二、刚体的运动描述为了描述刚体在运动中的位置和运动状态，我们引入了坐标系和参考点的概念。
坐标系用于确定刚体的位置，而参考点则是确定刚体位置的基准点。
在刚体运动学中，我们通常使用笛卡尔坐标系来描述刚体的运动。
通过选择合适的参考点，我们可以确定刚体的位置矢量。
三、刚体的位移、速度和加速度刚体的位移是指刚体在运动过程中，由一个位置变换到另一个位置的变化量。
刚体的速度是指刚体在单位时间内所发生的位移。
刚体的加速度是指刚体速度的变化率，即单位时间内速度的变化量。
在刚体运动学中，我们可以通过求导数的方法来计算刚体的速度和加速度。
四、刚体运动的基本公式刚体运动学中有一些基本的公式，可以帮助我们计算刚体的运动参数。
其中，最基本的公式是位移公式，即s = v * t，其中s表示位移，v表示速度，t表示时间。
通过这个公式，我们可以计算刚体在给定时间内的位移量。
另外，我们还可以使用速度公式和加速度公式来计算刚体的速度和加速度。
五、刚体运动的特殊情况在刚体运动学中，存在一些特殊的情况，需要特别注意。
例如，当刚体做匀速直线运动时，速度和加速度都是常量。
当刚体做匀加速直线运动时，速度是随时间线性增加的，而加速度是常量。
此外，当刚体做曲线运动时，速度和加速度的方向可能随时间变化。
六、刚体运动学的应用刚体运动学在实际生活中有着广泛的应用。
例如，在机械工程中，我们可以利用刚体运动学的原理来设计机械装置和机器人。
3-1刚体的基本运动
3－1
刚体的基本运动
例3-1 一半径 r 0 .5 0 m 的飞轮,转速n 6 0 0 r m in 1 , 制动后转过 1 0 圈而静止.设转动过程中飞轮作匀变 速转动.求:(1)转动过程中飞轮的角加速度和经过的 时间;(2)在1 s末时,飞轮边缘某点的线速度、切向加 速度和法向加速度.
0
0
第三章 刚体的定轴转动
3－1
刚体的基本运动
t d dt
瞬时角速度（角速度）
lim
t 0
刚体定轴转动（一维转动）的转动方向可以 用角速度的正负来表示 .
z
面对 O z 轴方向观察, 如果 0,刚体逆时 针转动;反之,刚体顺 时针转动.
z
0
0
1
3 1 .4 rad s
1
轮边缘某点的线速度
v r 0 .5 3 1 .4 m s
1
1 5 .7 m s
1
切向加速度
a t r 0 .5 3 1 .4 m s
2
1 5 .7 m s
2
法向加速度
a n r
3－1
刚体的基本运动
三、 匀变速转动公式 匀变速转动：当刚体绕定轴转动的角加速度为 恒量时的转动. 刚体匀变速转动与质点匀变速直线运动公式对比 质点匀变速直线运动
v v 0 at
x x0 v 0t 1 2 at
2
刚体绕定轴作匀变速转动
0 t
0 0t
第三章作业 P83
15、17、18、19、21、23
第三章 刚体的定轴转动
解 （1） 0 5 π rad s
刚体力学基础详解
(2) 如以重量P =98 N的物体挂在绳端，试计 算飞轮的角加速。
rO T
解 (1) FrJ F r9 80.23.2 9rad 2 /s
J 0.5 (2) m gTma
F mg
TrJ ar
J
mgr mr2
两者区别
0.59 1 80 0.2 0.222.1 8rad 2 /s
例 圆盘以 0 在桌面上转动,受摩擦力而静止
3. 一般运动
刚体不受任何限制的的任意运动称为刚体
的一般运动。它可视为以下两种刚体的基
本运动的叠加：
随基点O（可任 选）的平动
FMac
绕通过基点O的瞬时 轴的定轴转动
质点运动
本章主要讨论
§5.2 刚体绕定轴转动运动学
z 组成刚体的各质点都绕同一直线 做圆周运动 _____ 刚体转动。
转轴固定不动 — 定轴转动
当 M 为零时，则刚体保持静止或匀速转动
实验证明 当存在 M 时， 与 M 成正比
M
在国际单位中 M J
刚体的转动定律 Mz J
作用在刚体上所有的外力对 定轴 z 轴的力矩的代数和
推论
刚体对 z 轴 的转动惯量
(1) M 正比于 ，力矩越大，刚体的 越大
(2) 力矩相同，若转动惯量不同，产生的角加速度不同
dr
J0 m r2 d m 0 R2 R m 2r3 d rm 2R 2
O
Rm dr
r O
(3) J 与转轴的位置有关
z
z
M
L
M
L
O
dx
x
O dx
x
J Lx2dx1M2L
0
3
J L/2x2dx1M2L
刚体运动的基本原理
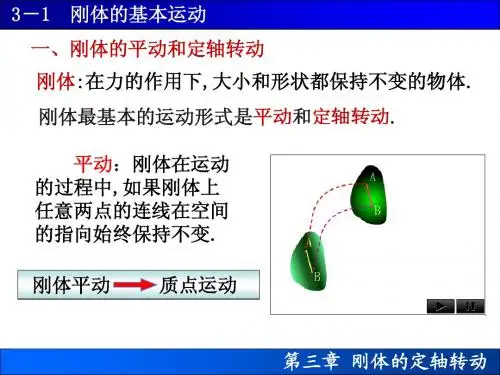
刚体运动的基本原理刚体运动是物体在空间中做整体性的运动，不发生形变的运动。
刚体运动的基本原理可以通过以下几个方面来解释：一、质点的运动质点可以看作是质量无限大的一个点，它不发生形变，仅产生平移运动。
质点的平移运动可以用牛顿第一定律来描述，即物体在不受外力作用时将保持静止或者匀速直线运动。
这是因为质点不受力的影响，所以它的速度和位置都不会改变。
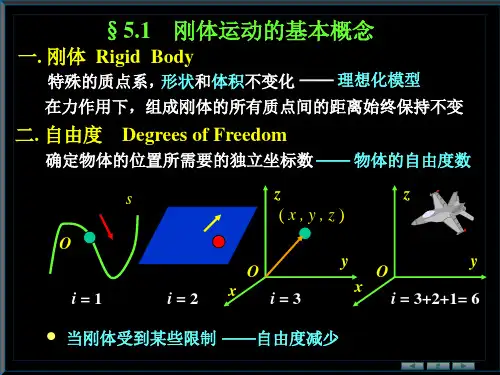
二、刚体的自由度刚体在空间中的运动由其自由度决定。
自由度是指刚体能够独立运动的最小数量。
对于一个刚体而言，它的自由度取决于它的维度。
在三维空间中，一个刚体有6个自由度，分别为三个平移自由度和三个转动自由度。
三、刚体的平移运动刚体的平移运动是指它在空间中沿着直线运动，整体上保持不变。
刚体的平移运动可以由质点的运动来描述。
当一个刚体受到一个外力时，该外力会作用在刚体的重心上，使得刚体产生平移运动。
刚体的平移加速度与作用在刚体上的合力成正比，与刚体的质量成反比。
四、刚体的转动运动刚体的转动运动是指它在空间中绕轴线旋转，整体上保持不变。
刚体的转动运动可以由刚体的转动惯量来描述。
转动惯量是刚体旋转惯性的量度，与刚体的质量分布以及轴线的位置有关。
当一个刚体受到一个力矩时，该力矩会使刚体产生转动运动。
刚体的转动加速度与作用在刚体上的合力矩成正比，与刚体的转动惯量成反比。
五、刚体的复合运动刚体可以进行平移和转动的复合运动。
当一个刚体受到既有平移又有转动的外力时，刚体既会发生平移运动，也会发生转动运动。
刚体的平移和转动是相互独立的，但它们会同时发生。
六、刚体碰撞的基本原理当两个刚体碰撞时，根据动量守恒定律和动能守恒定律，可以得到碰撞前后刚体的动量和动能之间的关系。
在完全弹性碰撞中，刚体在碰撞过程中既满足动量守恒定律，也满足动能守恒定律。
在非完全弹性碰撞中，刚体在碰撞过程中会发生能量损失，动能不守恒。
总结：刚体运动的基本原理包括质点的运动、刚体的自由度、刚体的平移和转动运动，以及刚体碰撞的原理。
刚体的运动及描述
v r
P点线加速度 an r
2
dv at r dt
z
ω ,α v r θ
匀角加速转动的运动学关系：
P
参 考 方 向
0 t ( 0 ) 0 t 1 t 2 2 2 2 0 2 ( 0 )
刚体
r O ×
定轴
第5章 刚体力学基础
5-1 刚体的运动及描述
矢量形式
v r 2 an r at r
或： a t r e
刚体定轴转动(一维转动) 的转动方向可以用角速 度的正、负来表示。 角加速度
第5章 刚体力学基础
5-1 刚体的运动及描述
定点转动：
运动中刚体上只有一点固定不动，整个刚体绕过该固
定点的某一瞬时轴线转动.
如：陀螺的运动
i3
（转轴方向（2），绕轴转角（1））
第5章 刚体力学基础
5-1 刚体的运动及描述
3 平面平行运动 刚体上各点都平行于某一固定平面的运动称为刚体的 平面运动，又称为刚体的平面平行运动。 如：车轮直线滚动 可以分解为： 刚体随质心的平动（i=2） 和绕质心垂直于运动平 面的定轴转动（i=1）
·
Δ
· o
o
第5章 刚体力学基础
5-1 刚体的运动及描述
刚体的一般运动可看作： 随质心的平动 + 绕质心的转动 的合成
第5章 刚体力学基础
5-1 刚体的运动及描述
5.1.3 刚体定轴转动的运动学描述
定轴转动：刚体上任意点都绕同一 轴在各自的转动平面内作圆周运动。
O
z
ω
r P’(t+dt) d P(t)
第六章 运动学基础2
a2
at 2
an2
(v2
c2 )a2 v2
(v2 )2
(1
v2 c2 v2
)a2
v4
2
c2 v2
a2
v4
2
a v3 (负号不合理舍去）
c
v2 c2 a v
§ 6-3 刚体的平动
一、定义 Translational motion of a rigid body
z 刚体在运动过程中，其上任
点的切向加速度和法向加速度的大小分别为：
a v 0 ,
an
v2
80
因为： a a2 an2 32 an
所以：
v2 80
an 32
即： ρ = 2.5 （m)
例6-7 半径为r的轮子沿直线轨道无滑动的滚动（称为纯滚
动），设轮子转角=t，如图所示。求用直角坐标和弧坐标表
示的轮缘上任一点M的运动方程，并求该点的速度、切向加速
5. 点的加速度
v vτ
a dv dv τ v dτ dv τ v dτ ds dv τ v2 dτ
dt dt dt dt ds dt dt
ds
dv τ v2 n
dt
①②
dτ 1 n
ds
at an
①切向加速度at---反映速度的大小随 时间的变化率，方向沿切线方向。
v2
at dt , an
v
a
aE
v D
a
F a v
aG v =0
提示：图示各点的速度均为可能，在速度可能的情况下， 点 C,E, F,G 的加速度为不可能，点 A,B,D 的加速度为可能
例6-5 列车沿半径为R=800m的圆弧轨道作匀加速运动。 如初速度为零，经过2min后，速度到达54km/h。求列车 起点和未点的加速度。
刚体力学
转动定律
M J
3) M ——外力矩之和，而不是合外力之矩。
4)适用条件：惯性系 两类基本问题:
1) 地位等同于平动问题中的牛顿第二定律，适于研究刚体转动 的瞬时效应； 2)对于有固定转轴的刚体转动，转动定理可以写为标量式， Mz = Jβz 此时，外力、位矢应当分解到与转轴垂直的平面内。
A.已知刚体转动状态求刚体所受力矩
——力矩的瞬时效应
上午5时46分
9
力矩——改变物体转动状态的原因
1、力对固定点的力矩
1）定义：作用于质点的力对惯性系 中某参考点的力矩，等于力的作用 点对该点的位矢与力的矢积，即
M r F
M
o
－－力矩是矢量 大小：
r
F
m
方向： 垂直于 r 和 F 所决定的平面，其指向用右手螺旋法则
F
F
B）力的方向沿矢径的方向
r
sin 0
力对固定轴的力矩为零的情况：
若力的作用线与轴平行 若力的作用线与轴相交
则力对该轴无力矩作用
。
上午5时46分
14
合力矩等于各分力矩的矢量和
M M1 M 2 M 3
f ji
质点系内一对内力对任一点的力矩之矢量和为零
M i 0 M j 0 ri fij rj f ji f ij f ji
M i 0 M j 0 (r j ri ) f ji r ji f ji 0
上午5时46分
rj
j
rji
i
o
ri
f ij
上午5时46分
3
转动：刚体中所有的点都绕同一直线做圆周运动. 定轴转动、非定轴转动
理论力学练习册及答案
8-7.四杆机构中，曲柄OA以匀角速度ω0=25 rad/s绕O轴转动，OA=50 cm，AB=100 cm，O1B= cm。求∠OAB=900时，B点的加速度，摇臂O1B的角速度和角加速度。
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解：将力系向A点简化，并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋，
作用点为：
3-2.已知A（1，0，1），B（0，1，2）（长度单位为米），F= kN。求力F对x、y、z轴的矩？
解：
3-3.如图所示，长方体边长为a、b、c，力F沿BD，试计算力F对AC轴之矩MAC(F)
解：力F对C点的矩为：
4-3.置于铅垂面内的均质正方形簿板重P= 100kN，与地面间的摩擦系数f= 0.5，欲使簿板静止不动，求作用在点A的力F的最大值？
4-4.折梯放在水平地面上，其两脚与地面的摩擦系数分别为fA= 0.2，fB= 0.6，折梯一边AC的中点D上有一重为P= 500N的重物，折梯重量不计，问折梯能否平衡？如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1．在如图所示中，已知ω、。在图上标示出A、B两的速度、加速度。
6-2．在如图所示的平面机构中，半径为r的半圆盘在A和B处与杆铰接，已知 ， ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3．在如图所示的平面机构中，齿轮1紧固在杆AC上， ,齿轮1与半径为r2的齿轮2啮合，齿轮2可绕O2轴转动，。设 ， ，试确定 时，轮2的角速度和角加速度。
解：动点取曲柄OA上A点，
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解：将力系向A点简化，并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋，
作用点为：
3-2.已知A（1，0，1），B（0，1，2）（长度单位为米），F= kN。求力F对x、y、z轴的矩？
解：
3-3.如图所示，长方体边长为a、b、c，力F沿BD，试计算力F对AC轴之矩MAC(F)
解：力F对C点的矩为：
4-3.置于铅垂面内的均质正方形簿板重P= 100kN，与地面间的摩擦系数f= 0.5，欲使簿板静止不动，求作用在点A的力F的最大值？
4-4.折梯放在水平地面上，其两脚与地面的摩擦系数分别为fA= 0.2，fB= 0.6，折梯一边AC的中点D上有一重为P= 500N的重物，折梯重量不计，问折梯能否平衡？如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1．在如图所示中，已知ω、。在图上标示出A、B两的速度、加速度。
6-2．在如图所示的平面机构中，半径为r的半圆盘在A和B处与杆铰接，已知 ， ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3．在如图所示的平面机构中，齿轮1紧固在杆AC上， ,齿轮1与半径为r2的齿轮2啮合，齿轮2可绕O2轴转动，。设 ， ，试确定 时，轮2的角速度和角加速度。
解：动点取曲柄OA上A点，
工程力学第三版电子课件模块四刚体的基本运动
如图所示为渐开线齿轮齿条传动机构简图，已知齿轮转速 n=15 r/min，齿 轮的齿数z=30，模数 m=2 mm，试计算齿轮与齿条啮合点 M 的速度及齿条移 动速度 v 的大小。
渐开线齿轮齿条传动机构简图
1—齿轮 2—齿条
142
相关知识 一、刚体的平行移动
1．刚体平行移动的定义 这些运动的共同特点：刚体在运动过程中，刚体内任一直线始终与初始位 置保持平行。这种运动称为刚体的平行移动，简称刚体平动。
148
摩天轮
汽车车轮
149
2．定轴转动刚体的转速、角速度与角加速度 （1）转速 工程上常以每分钟的转数表示刚体转动的快慢程度，称为转速，用字母 n 表示，单位为 r/min（转 / 分）。 （2）角速度 单位时间内转过的角度称为角速度，用字母ω 表示，单位为 rad/s（弧度 / 秒）。
150
（3）角加速度 角速度ω 随时间 t 的变化率称为角加速度，用符号ε表示。 角加速度ε是角速度ω 对时间的一阶导数，或者等于转角 φ 对时间的二阶导 数，即：
任务一 任务二
刚体的平行移动与定轴转动 定轴转动刚体上各点速度和加速度计算
139
140
学习目标
1．理解刚体平行移动（简称平动）和定轴转动（简称转动）的定义。 2．掌握刚体平动和转动的特点，并正确判断刚体是平动还是转动。 3．掌握刚体定轴转动的转动方程及角速度、角加速度的计算方法。
141
任务描述
起吊装置 156
相关知识 一、定轴转动刚体上各点的线速度与加速度
1．线速度 转动刚体上某点单位时间内转过的弧长称为线速度，用字母 v 表示，常用 单位为m/min（米 / 分）或 m/s（米 / 秒）。 线速度的方向沿轨迹的切线方向，如图a 所示，即垂直于半径 OM，指向 与ω 转向一致。由上式可知，转动刚体上各点的线速度与它们的转动半径成 正比。线速度沿半径的分布情况如图b 所示。
渐开线齿轮齿条传动机构简图
1—齿轮 2—齿条
142
相关知识 一、刚体的平行移动
1．刚体平行移动的定义 这些运动的共同特点：刚体在运动过程中，刚体内任一直线始终与初始位 置保持平行。这种运动称为刚体的平行移动，简称刚体平动。
148
摩天轮
汽车车轮
149
2．定轴转动刚体的转速、角速度与角加速度 （1）转速 工程上常以每分钟的转数表示刚体转动的快慢程度，称为转速，用字母 n 表示，单位为 r/min（转 / 分）。 （2）角速度 单位时间内转过的角度称为角速度，用字母ω 表示，单位为 rad/s（弧度 / 秒）。
150
（3）角加速度 角速度ω 随时间 t 的变化率称为角加速度，用符号ε表示。 角加速度ε是角速度ω 对时间的一阶导数，或者等于转角 φ 对时间的二阶导 数，即：
任务一 任务二
刚体的平行移动与定轴转动 定轴转动刚体上各点速度和加速度计算
139
140
学习目标
1．理解刚体平行移动（简称平动）和定轴转动（简称转动）的定义。 2．掌握刚体平动和转动的特点，并正确判断刚体是平动还是转动。 3．掌握刚体定轴转动的转动方程及角速度、角加速度的计算方法。
141
任务描述
起吊装置 156
相关知识 一、定轴转动刚体上各点的线速度与加速度
1．线速度 转动刚体上某点单位时间内转过的弧长称为线速度，用字母 v 表示，常用 单位为m/min（米 / 分）或 m/s（米 / 秒）。 线速度的方向沿轨迹的切线方向，如图a 所示，即垂直于半径 OM，指向 与ω 转向一致。由上式可知，转动刚体上各点的线速度与它们的转动半径成 正比。线速度沿半径的分布情况如图b 所示。
刚体的基本运动
rB
rAB
vB rB与 vA rA
O
A rA
d d r A t B r B r A ( r B r A ) r AB
此结果表示：
当转动刚体上的一个大小不变的矢量，只要其方向发生变化， 其对时间的变化率等于刚体的角速度与本矢量的叉积。
整理课件
推论：若在转动刚体上，固结一组坐标系 Oxyz ，
整理课件
例3 轮系传动
1、皮带轮传动
v1=v=v2
v1=r11;
v2= r22;
i r2 1 n1 r1 2 n2
v1 n1 r1
v
n2 r2 v2
整理课件
2、齿轮传动
r11r22 r11= –r22;
i1 2
1 2
n1 n2
r2 r1
z2 z1
r1
r2
整理课件
3、齿轮箱传动
1 z2 ;
其相应的单位矢量为i ，j ，k ，该坐标系
随同刚体以角速度 绕某轴转动，则必定有：
di d t d j d t dk dt
i
j
k
泊桑公式
整理课件
解:
i14
1 4
z2 z4 z1 z3
z1
z2
1
(1)齿轮对数从 主
动 动
齿 齿
轮 轮
数乘 数乘
积 积
z4 4 z3 r
476 0 2 0 0 143 2 1 2 22 58 3.94
v
v=4r=3.94 m/s
角速度: 4 / 1 =0.05
整理课件
例5
已知： O 1AO 2B2r,0＝常数，
an|t20
a
|t2
刚体的运动方程
(欧勒运动学方程)
若：已知 ω 1 , ω 2 , ω 3
& & & 则：计算 ϕ , ψ , θ
讨论：对于对称陀螺，两个主轴可在平面 x1 x 2 上任意 选取，则：取 ox1 沿oN方向 ⇒
& ψ =0& 于是有： ω Nhomakorabea = θ
& & & ω 2 = φ sin θ ω 3 = φ sin θ + ψ
又
rc
∑m r = ∑m
a a a
a a
=0
⇒ 则
∑m r
a
a a
=0
d & 0 + ∑ (ra × ma ra ) = ∑ ra × Fa 外 dt a a
⇒
d & ∑ (ra × mara ) = ∑ ra × Fa 外 dt a a
令
& L( o ) = ∑ ra × ma ra
a
M ( o ) = ∑ ra × Fae
ϕ ：刚体绕固定轴oz转过的角度——进动角； & ϕ ：进动角速度——沿oz方向
& ψ
ψ ：刚体绕 ox3 转过的角度——自转角；
：自转角速度——沿 ox3 方向。
ox θ ： 3 和oz间的夹角——章动角； θ& ：章动角速度——沿oN方向。
1． & 在 x1 x 2平面， 在 θ 由图：
x1 , x 2 , x3 的分量 θ&1 , θ&2 , θ&3 。
dω d ' ω d 'ω = + ω×ω = [ ] dt dt dt
⇒
dv 0 & = w + a + 2ω × v + ω × r + ω × (ω × r ) dt
刚体转动知识点总结
刚体转动知识点总结1. 刚体的定义在物理学中，刚体是一个理想化的概念，用来描述物体的力学性质。
刚体是一个不会发生形变的物体，它具有不变的形状和大小。
在刚体转动的过程中，可以忽略物体的形变，只需考虑刚体的质量分布和外力作用情况。
2. 转动定律在刚体转动的过程中，存在着转动定律，即牛顿第二定律在转动运动中的应用。
根据转动定律，刚体的角加速度与作用在刚体上的合外力成正比，与刚体的转动惯量成反比。
转动定律可以用数学公式表示为：\[ \tau = I \alpha \]其中，$\tau$ 表示合外力矩，$I$ 表示刚体的转动惯量，$\alpha$ 表示刚体的角加速度。
3. 角动量角动量是描述刚体转动运动的物理量，它是刚体的转动惯量和角速度的乘积。
角动量可以用数学公式表示为：\[ L = I \omega \]其中，$L$ 表示角动量，$I$ 表示刚体的转动惯量，$\omega$ 表示角速度。
4. 转动惯量转动惯量是描述刚体对转动运动的惯性大小的物理量，它反映了刚体的质量分布对其转动运动的影响程度。
转动惯量的计算需要考虑刚体的形状和质量分布，通常需要使用积分来进行计算。
5. 转动运动方程刚体转动运动的规律可以通过转动运动方程来描述，转动运动方程可以表示为：\[ \tau = \frac{dL}{dt} \]其中，$\tau$ 表示合外力矩，$L$ 表示角动量，$t$ 表示时间。
转动运动方程描述了刚体的转动运动受到外力矩作用时角动量的变化规律。
6. 刚体的转动运动在刚体的转动运动中，需要考虑刚体的转动惯量、角速度、角加速度等物理量。
刚体的转动运动可以在直角坐标系下进行描述，通过使用牛顿运动定律和转动运动方程来分析刚体的转动运动规律。
7. 平行轴定理和垂直轴定理在计算刚体的转动惯量时，可以利用平行轴定理和垂直轴定理来简化计算过程。
根据平行轴定理和垂直轴定理，刚体绕与其质心平行（或垂直）且距离为$d$的轴转动的转动惯量可以表示为：\[ I = I_{\text{CM}} + Md^2 \]其中，$I$ 表示绕过质心平行（或垂直）轴转动的转动惯量，$I_{\text{CM}}$ 表示绕质心转动的转动惯量，$M$ 表示刚体的质量，$d$ 表示轴与质心的距离。
刚体基本运动
2 2
即：转动刚体内任一点的法向加速度(又称向心加速度)的大小， 等于刚体角速度的平方与该点到轴线的垂直距离的乘积，它的 at 方向与速度垂直并指向轴线。
w
a
M
r a n
j
s
M0
O
2.3 转动刚体内各点的速度和加速度
点的全加速度为：
a
at
j
a at 2 an2 R a 2 w 4 at a tan 2 an w
2.1 刚体的平行移动
如果在物体内任取一直线段，在运动过程 中这条直线段始终与它的最初位置平行，这种 运动称为平行移动，简称平动。
此处有影片播放
2.1刚体的平行移动
C
D
A
摆式输送机的料槽 筛分机构
B
直线行驶的列车车厢
2.1刚体的平行移动
在刚体上任取两点，令A的矢径为rA, B的矢径为rB,两条 矢端曲线是两点的轨迹。
动点的速度矢等于它的矢径对时间的一阶导数。
r dr v lim dt t 0 t
动点的速度矢沿着矢径的矢端曲线的切线，即沿 动点运动轨迹的切线，并与此点运动的方向一致。
1.1 矢量法
3. 加速度 点的速度矢对时间的变化率称为加速度。点的加 速度也是矢量，它表征了速度大小和方向的变化。 点
1.3 自然法
全加速度为at和an的矢量和
a a t an
全加速度的大小和方向由下列二式决定：
v
大小：
at
a a t an
2
2
M
方向：
| at | tan an
an
a
例2：下图为料斗提升机示意图。料斗通过钢丝绳由绕水平轴O 转动的卷筒提升。已知：卷筒的半径为R＝16cm，料斗沿铅垂提 升的运动方程为y＝2t2，y以cm记，t 以s计。求卷筒边缘一点M在 t＝4s时的速度和加速度。
即：转动刚体内任一点的法向加速度(又称向心加速度)的大小， 等于刚体角速度的平方与该点到轴线的垂直距离的乘积，它的 at 方向与速度垂直并指向轴线。
w
a
M
r a n
j
s
M0
O
2.3 转动刚体内各点的速度和加速度
点的全加速度为：
a
at
j
a at 2 an2 R a 2 w 4 at a tan 2 an w
2.1 刚体的平行移动
如果在物体内任取一直线段，在运动过程 中这条直线段始终与它的最初位置平行，这种 运动称为平行移动，简称平动。
此处有影片播放
2.1刚体的平行移动
C
D
A
摆式输送机的料槽 筛分机构
B
直线行驶的列车车厢
2.1刚体的平行移动
在刚体上任取两点，令A的矢径为rA, B的矢径为rB,两条 矢端曲线是两点的轨迹。
动点的速度矢等于它的矢径对时间的一阶导数。
r dr v lim dt t 0 t
动点的速度矢沿着矢径的矢端曲线的切线，即沿 动点运动轨迹的切线，并与此点运动的方向一致。
1.1 矢量法
3. 加速度 点的速度矢对时间的变化率称为加速度。点的加 速度也是矢量，它表征了速度大小和方向的变化。 点
1.3 自然法
全加速度为at和an的矢量和
a a t an
全加速度的大小和方向由下列二式决定：
v
大小：
at
a a t an
2
2
M
方向：
| at | tan an
an
a
例2：下图为料斗提升机示意图。料斗通过钢丝绳由绕水平轴O 转动的卷筒提升。已知：卷筒的半径为R＝16cm，料斗沿铅垂提 升的运动方程为y＝2t2，y以cm记，t 以s计。求卷筒边缘一点M在 t＝4s时的速度和加速度。
理论力学运动学习题及详解
y f 2 (t ) z f 3 (t )
2 2
a x x a y y a z z
2 2 2
v vx v y vz
2
a ax a y az
方向均由相应的方向余弦确定。
第2章 运动学练习
二．基本公式 自然法（轨迹已知时）
运动方程 速度
ae 5 2 0 r 4
5 2a r0 4
B
aC 0
O2
3销钉C固定在AB杆，在滑槽O2D中运动，该瞬时O1A与AB水平，O2D
铅直，且O1A=AC=CB=O2C=r，ω0=常数,求
AB、O2 D、 AB、O2 D .
D
n aCA
（2）加速度分析
AB 0
a 常量， an 0
，点做何种运动（ B）。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ，其轨迹方程为(
B)
A.3x 4 y 36 0, C.2 x 2 y 24 0,
第2章 运动学练习
B.3x 2 y 18 0 D.2 x 4 y 36 0
1.选择题：
【练习题】
(4). 如图所示平面机构中，O1A=O2B= r, O1O2 =AB, O1A以匀角速度绕垂直于图 面的O1轴转动，图示瞬时，C点的速度为：( D )
A.
B. C.
Vc 0
Vc r a
2 2
水平向右
O1 A
O2
Vc r0 D. Vc r0
铅直向上 水平向右
2.刚体运动学
基本运动 平面运动
理论力学8刚体的基本运动
前面都为数量表达式，只有大小，而未标明方向； 矢量表达既有大小，又有方向。
一. 角速度和角加速度的矢量表示
按右手定则规定
w ， 的方向。
大小:|w ||ddt |
dw dw k k
dt dt
方向如图 w wk
15
二 刚体内任一点的线速度和线加速度的矢积表示
vRw rsin w |w r|wrsin Rw
小于90o , 在同一瞬间的速度和加速度的分布图为:
各点速度分布图
各点加速度分布图
10
§8-4 绕定轴转动刚体的传动问题
传动比：通常称主动轮与从动轮角速度之比
i12
w1 w2
一.齿轮传动
因为是做纯滚动(即没有相对滑动) 1.内啮合
vF vE vF vE
wF rF wE rE
定义齿轮传动比
iEF
aC n Rw02 0.532 4.5m/s 2
aC (aC )2 (aC n )2 12 4.52 4.61 m/s2
tg
aC aC n
1 4.5
0.222,
12.5
⑤ t=3s 时， aC aA 1m/s2,aCn Rw 2 0.592 40.5m/s2
aC
12 40.52 40.51m/s2,
w 2 w02 2
7
§8-3 转动刚体内各点的速度和加速度
一. 线速度V和角速度w之间的关系(即角量与线量的关系)
w , 对整个刚体而言(各点都一样)；
v, a 对刚体中某个点而言(各点不一样)。
v
v
lim
t0
R t
wR
v wR
8
二.角加速度 与an ,a 的关系
理论力学参考答案第6章盛冬发
第6章 运动学基础一、是非题(正确的在括号内打“√”、错误的打“×”)1．动点速度的大小等于其弧坐标对时间的一阶导数，方向一定沿轨迹的切线。
( √ ) 2． 动点加速度的大小等于其速度大小对时间的一阶导数，方向沿轨迹的切线。
( × ) 3．在实际问题中，只存在加速度为零而速度不为零的情况，不存在加速度不为零而速度为零的情况。
( × ) 4．两个刚体做平动，某瞬时它们具有相同的加速度，则它们的运动轨迹和速度也一定相同。
( × ) 5．定轴转动刚体的角加速度为正值时，刚体一定越转越快。
( × ) 6．两个半径不等的摩擦轮外接触传动，如果不出现打滑现象，两接触点此瞬时的速度相等，切向加速度也相等。
( √ )二、填空题1. 描述点的运动的三种基本方法是矢径法、直角坐标法和自然坐标法。
2. 点做圆周运动，加速度由切向加速度和法向加速度组成，其中切向加速度反映了速度大小随时间的变化率，方向是沿圆周的切线；法向加速度反映了速度的方向随时间的变化率，方向是沿圆周的法线。
3. 质点运动时，如果d d st和22d d s t 同号，则质点做加速运动，反之则做减速运动。
4. 刚体运动的两种基本形式为平动和定轴转动。
5. 刚体平动的运动特征是刚体在运动的过程中其内的任一直线始终和原来的位置平行。
6. 定轴转动刚体上点的速度可以用矢积表示，它的表达式为r ωv ⨯=；刚体上点的加速度可以用矢积表示，它的表达式为v ωr εa ⨯+⨯=。
7. 刚体绕定轴转动时，在任一瞬时各点具有相同的角速度和角加速度，且各点轨迹均为 圆周。
8. 定轴转动刚体内点的速度分布规律为任何一条通过轴心的直径上各点的速度，若将速度矢的端点连成直线，此直线通过轴心。
9. 半径均为R 的圆盘绕垂直于盘面的O 轴做定轴转动，其边缘上一点M 的加速度如图6.23所示，试问两种情况下圆盘的角速度和角加速度的大小分别为：图(a)：=ω0；=εRa。
大学物理刚体运动学
大学 物理
4-1 刚体运动学
4.1.1 刚体：在外力作用下，形状和大小都不发生变化的物体 .
4.1.2 刚体的基本运动形式：
（1）平动：若刚体中所有点的 运动轨迹都保持完全相同，或者 说刚体内任意两点间的连线在各 时刻总是平行.
刚体平动
质点运动
（2）转动： 定轴转动、定点转动
定轴转动: 转轴在所选参考系中固定不动的转动
dt 2
vi ri vi ri
第四章 刚体力学
2
➢ 刚体的一般运动 质心的平动 + 绕质心的转动
第四章 刚体力学
1
大学 物理
4-1 刚体运动学
4.1.3 描述刚体定轴转动的物理量
特征：刚体中所有的质点具有相同的
角位移、角速度、角加速度
角位移
角速度
d
dt
ri
vi • mi
转动平
面
O
图4-3线速度和角速度之间的矢量关系角加速度ddtd2
4-1 刚体运动学
4.1.1 刚体：在外力作用下，形状和大小都不发生变化的物体 .
4.1.2 刚体的基本运动形式：
（1）平动：若刚体中所有点的 运动轨迹都保持完全相同，或者 说刚体内任意两点间的连线在各 时刻总是平行.
刚体平动
质点运动
（2）转动： 定轴转动、定点转动
定轴转动: 转轴在所选参考系中固定不动的转动
dt 2
vi ri vi ri
第四章 刚体力学
2
➢ 刚体的一般运动 质心的平动 + 绕质心的转动
第四章 刚体力学
1
大学 物理
4-1 刚体运动学
4.1.3 描述刚体定轴转动的物理量
特征：刚体中所有的质点具有相同的
角位移、角速度、角加速度
角位移
角速度
d
dt
ri
vi • mi
转动平
面
O
图4-3线速度和角速度之间的矢量关系角加速度ddtd2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
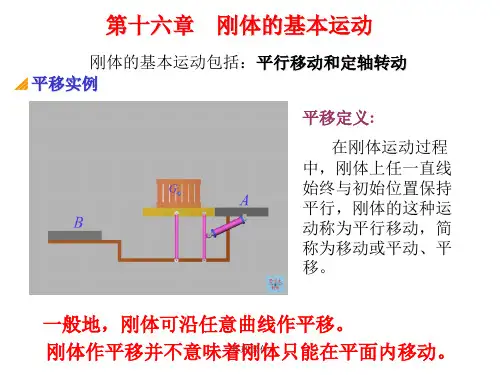
第6章 刚体的基本运动在上一章的基础上本章的研究对象是刚体，学习的内容是刚体的平行移动和定轴转动，它构成刚体的两个基本运动，也是研究刚体复杂运动的基础。
6.1 刚体平行移动工程实际中，如气缸内活塞的运动，打桩机上桩锤的运动等等，其共同的运动体点是在运动过程中，刚体上任意直线段始终与它初始位置相平行，刚体的这种运动称为平行移动，简称平移。
如图6-1所示车轮的平行推杆AB 在运动过程中始终与它初始位置相平行，因此推杆AB 作平移。
确定平移刚体的位置和运动状况，只需研究刚体上任意直线段AB ，A 、B 两点的矢径为A r 和B r ，A 、B 两点间的有向线段AB r 之间的关系为AB B A r r r += （6-1）图6-1图6-2由平动定义知AB r 为恒矢量，A 、B 两点的轨迹只相差AB r 的恒矢量，即A 、B 两点的轨迹形状相同。
式（6-1）对时间求导，得B A v v = （6-2） B A a a = （6-3）结论：（1）平移刚体上各点的轨迹形状相同；（2）在同一瞬时平移刚体上各点的速度相等，各点的加速度相等。
因此，刚体的平行移动可以转化一点的运动来研究，即点的运动学。
6.2 刚体的定轴转动工程实际中绕固定转动的物体很多，如飞论、电动机的转子、卷扬机的鼓轮、齿轮等均绕定轴转动。
这些刚体的运动特点是：在运动过程中，刚体上存在一条不动的直线段，刚体的这种运动称为刚体的绕定轴转动，简称转动，转动刚体的不动的直线段称为刚体的转轴。
6.2.1转动刚体的运动描述如图6-3所示，选定参考坐标系oxyz ，设z 轴与刚体的转轴重合，过z 轴作一个不动的平面0P （称为静平面），再作一个与刚体一起转动的平面P （称为动平面），令静平面0P 位于oxz 面上，初始瞬时这两个平面重合，当刚体转动到t 瞬时，两个平面间的夹角为ϕ，ϕ称为刚体的转角，用来描述转动刚体的代数量。
按照右手螺旋法则规定转角ϕ的符号，其单位为弧度（rad ）。
刚体定轴转动的运动方程是f(t)=ϕ （6-4）f(t)是时间t 的单值连续函数。
角速度是描述刚体转动快慢的物理量，用ω表示，即转角ϕ对时间t 的导数，）或ϕϕ==(dtd ω （6-5） 单位为弧度/秒（rad/s ），它是代数量。
当ϕ∆＞0，ω＞0；ϕ∆＜0，ω＜0。
角加速度是角速度ω对时间t 的导数，用α表示）（或ϕϕα ====ωdtd dt d ω22 （6-6） 单位为弧度/秒2（2rad/s ），它是代数量。
当α与ω同号时，刚体作加速转动；当α与ω异号时，刚体作减速转动。
工程中常用转速表示转动刚体的转动快慢，即每分钟转过的圈数，用n 表示，单位为转/分（m in)r/，角速度与转速的关系是30602nπn πω==（rad/s ） （6-7） 注意：转动刚体的运动微分关系与点的运动微分关系有着相似之处，望初学者加以比较。
6.2.2转动刚体上各点的速度和加速度当刚体作定轴转动时，刚体上各点均作圆周运动，故在刚体上任选一点M ，设它到转轴的距离为R ，如图6-4所示，当刚体转过ϕ角时 ，点M 的弧坐标为ϕR s = （6-8）图6-5式（6-8）对时间t 求导得点M 的速度为ωR v = （6-9） 其速度分布如图6-5所示。
式（6-9）对时间t 求导得点M 的切向加速度为αR a τ= （6-10）点M 的法向加速度为222ωR Rω)R (R v a n === （6-11）点M 的全向加速度为4222222ωR )ωR ()R (a a a n +=+=+=αατ （6-12）方向2ωa a tan n αθτ==（6-13） 其加速度分布如图6-6所示。
结论：（1）在同一瞬时，转动刚体上各点的速度v 和加速度a 的大小均与到转轴的垂直距离R 成正比；（2）在同一瞬时，各点速度v 的方向垂直与到转轴的距离R ，各点加速度a 的方向与到转轴的垂直距离R 的夹角θ都相等。
6.3 点的速度和加速度的矢量表示首先建立角速度的矢量概念，按照右手螺旋法则定义角速度的矢量表示为o图6-4图6-6k ωω= （6-14） 其中，k 为转轴z 的单位矢量，如图6-7a 所示。
刚体上任意一点M 的矢径r 、角速度ω和速度v 的矢量表示为r ×ω=v （6-15）同理，对于定轴转动刚体，定义角加速度的矢量概念，k ωαα== （6-16） 式（6-15）对时间t 求导得点M 加速度的矢量表示为v ωr αa ⨯+⨯= （6-17）如图6-7b 所示，式（6-17）右边第一项为切向加速度，第二项为法向加速度，即r αa τ⨯= v ωa n ⨯= （6-18） 结论：（1）作定轴转动刚体上任意一点的速度等于角速度矢与矢径的矢量积；（2）作定轴转动刚体上任意一点的切向加速度等于角加速度矢与矢径的矢量积，法向加速度等于角速度与速度的矢量积。
(a)(b)图6-7图6-8例题6-1如图6-8所示，曲柄OA 绕O 轴转动，其转动方程为24t =ϕ(rad)，BC 杆绕C 轴转动，且杆OA 与杆BC 平行等长，OA =BC =0.5m ，试求当s t 1=时，直角杆ABD 上D 点的速度和加速度。
解：由于OA 与BC 平行等长，则直角杆ABD 作平移，因此由平移的定义知：计算D 点的速度和加速度，只需计算A 点的速度和加速度即可。
曲柄OA 的角速度由式（6-5）得t dtd ω8==ϕ（rad/s ）曲柄OA 的角加速度由式（6-6）得8==dtd ωα（rad/s 2）当s t 1=时：（1）直角杆ABD 上D 点的速度 由式（6-9）得4850=⨯==.ωOA ωR =v （m/s ）方向垂直OA 指向角速度方向。
（2）直角杆ABD 上D 点的加速度 切向加速度由式（6-10）得4850=⨯==.OA αR =a τα（m/s 2） 法向加速度由式（6-11）得32850222=⨯==.ωOA ωR =a n （m/s 2）全向加速度由式（6-12）得：25323242222.=a +a =a n =+τ（m/s 2）全向加速度与法线间的夹角由式（6-13）得12508822.ω=a a =tan n ==αθτ其中o .137=θ。
例题6-2鼓轮O 轴转动，其半径为m 20.R =，转动方程为t t 42+-=ϕ(rad)，如图6-9所示。
绳索缠绕在鼓轮上，绳索的另一端悬挂重物A ，试求当s t 1=时，轮缘上的点M 和重物A 的速度和加速度。
图6-9解：鼓轮O 轴转动的角速度由式（6-5）得42+-==t dtd ωϕ（rad/s ）鼓轮O 轴转动的角加速度由式（6-6）得2-==dtd ωα（rad/s 2）当s t 1=时：（1）点M 的速度和加速度 由式（6-9）得40220..ωR =v M =⨯=（m/s ） 方向垂直R 指向角速度方向。
切向加速度由式（6-10）得40220.)(.αR =a M τ-=-⨯=（m/s 2）法向加速度由式（6-11）得8022022..ωR =a M n =⨯=（m/s 2） 全向加速度由式（6-12）得：8944080402222...=a +a =a nM M M =+τ（m/s 2）全向加速度与法线间的夹角由式（6-13）得502222.ω=a a =tan n =-=αθτ其中o .5726=θ。
（2）重物A 的速度和加速度 重物A 的速度为40.=v v M A =（m/s ）方向铅锤向下。
重物A 的加速度为40.=a a M τA -=（m/s 2）与速度方向相反，作减速运动。
例题6-3杆OB 绕O 轴转动，并套在套筒A 中，套筒A 在竖直滑道中运动，如图6-10所示。
已知套筒A 以匀速m /s 1=v 向上运动，滑道与O 轴的水平距离为m 40.l =，试求当杆OB 与水平线的夹角o 30=ϕ时，导的杆OB 的角速度和角加速度。
图6-10解：由几何关系得lvttan =ϕ （1） 由式（1）解得杆OB 绕O 轴转动的转动方程为lvttan 1-=ϕ （2）对式（2）求导的杆得OB 的角速度和角加速度为21)l(l v ω+==ϕ（3） 22322]1[2]1[2)lvt (t )l v ()l vt (l v )l vt (l v ωα+-=+-== （4） 当o 30=ϕ时，由式（1）得时间334030.v tan l t o ==代入式（3）和式（4），则杆OB 的角速度和角加速度为875134011401122.).(.)l vt (l v ω=⨯+=+==ϕ （rad/s ） n 图6-11064]34034011[33404012]1[2223223.)..(.).()l (t )l v (ωα-=⨯⨯+-=+-== （rad/s 2） 例题6-4变速箱由四个齿轮构成，如图6-11所示。
齿轮Ⅱ和Ⅲ安装在用一轴上，与轴一起运动，各齿轮的齿数分别为361=z 、1122=z 、323=z 和1284=z ，如主动轴Ⅰ的转数14501=n (r/min)，试求从动轮Ⅳ的转数4n 。
解：在机械中常用齿轮作为传动部件，例如本题中变速箱，是由多组齿轮构成的，起到增速和减速的作用。
在齿轮相互啮合处其速度应相等。
如本例中的主动轮Ⅰ和从动轮Ⅱ，设其角速度分别为1ω、2ω，齿轮的半径分别为1r 和2r ，即2211r ωr ω= （1）定义齿轮的传动比12i 等于主动轮的角速度与从动轮角速度的比。
由式（1）有122112r r ωωi ==（2） 由于齿轮啮合时齿距必须相等，而齿距等于齿轮节圆周长与齿轮齿数的比。
若设齿轮齿数分别为1z 、2z ，则有221122z r πz r π= （3） 从而由式（2）和由式（3）得12122112z z r r ωωi ===（4） 即齿轮传递时，两个齿轮角速度的比等于两个齿轮半径的反比，或等于两个齿轮齿数的反比。
在机械中还有皮带轮传动，如图如图6-12所示。
如不考虑皮带的厚度，并假设皮带与轮无相对滑动，设轮Ⅰ和轮Ⅱ的角速度分别为1ω、2ω，半径分别为1r 和2r ，即图6-122211r ωr ω= （5）皮带轮的传动比12i 为122112r r ωωi ==（6） 即皮带轮的传递时，两个皮带轮角速度的比等于两个皮带轮半径的反比。
由上面公式解本题。
设四个轮的转数分别为1n 、2n 、3n 、4n ，且有22n n = 122112z z n n i == 344334z z n n i ==将两式相乘得31424114z z z z n n i ==解得从动轮Ⅳ的转数4n 为11712811232361450423114=⨯⨯⨯==z z z z n n （r/min ） 6.4 本章小结1．刚体平行移动平行移动：在运动过程中，刚体上任意直线段始终与它初始位置相平行。