位置矢量运动方程位移速度加速度

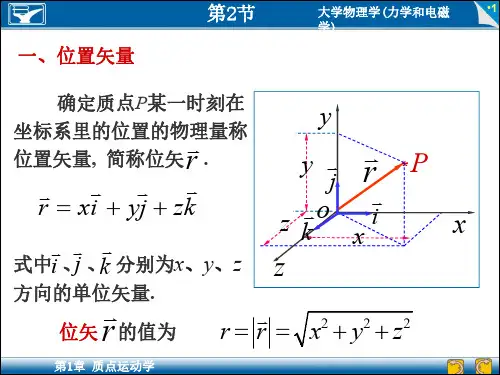
质点的位置矢量速度加速度之间的关系式质点的位置矢量、速度和加速度是物理学中描述质点运动的三个重要概念。

它们之间有着密切的关系，并且通过运动学的理论来描述。

首先，我们来定义这三个概念：1.位置矢量（r）：位置矢量是用来描述一个质点在空间中的位置的向量，通常用r表示。

位置矢量的方向与从参考点指向质点所在位置的方向一致，其大小表示参考点到质点之间的距离。

2.速度（v）：速度是描述质点在某一时刻的位置变化率的物理量，即质点单位时间内所经过的位移。

速度是一个矢量量，包括大小（也称为速率）和方向两个方面。

3.加速度（a）：加速度是描述质点在运动过程中速度变化率的物理量，即单位时间内速度的变化量。

加速度也是一个矢量量，包括大小和方向两个方面。

接下来，我们来分析位置矢量、速度和加速度之间的关系。

1.速度与位置矢量的关系：在运动学中，速度与位置矢量之间存在着微分关系，即速度矢量等于位置矢量对时间的导数（v = dr/dt）。

这意味着速度的大小可以表示为位置矢量的变化率，方向与位置矢量的方向一致。

速度矢量的微分形式可以表示为：v = dx/dt * i + dy/dt * j + dz/dt * k其中，i、j和k分别表示了空间中的三个坐标轴的单位矢量。

2.加速度与速度的关系：加速度是速度的变化率。

在运动学中，通过对速度矢量对时间的导数，可以得到加速度矢量（a），即a = dv/dt。

加速度的大小表示速度的变化率，方向与速度矢量的方向一致。

加速度矢量的微分形式可以表示为：a = dv/dt = d²x/dt² * i + d²y/dt² * j + d²z/dt² * k3.速度与加速度的关系：速度和加速度之间存在一种紧密的联系，即速度矢量又是加速度矢量对时间的积分。

换句话说，速度矢量等于加速度矢量对时间的积分，即v = ∫ a dt。

这说明了速度的变化是由加速度引起的，例如当质点受到作用力或者外界扰动时，会产生加速度，进而导致速度发生变化。

关于质点运动的矢量及其分量描述的一般讨论质点运动是物理学研究的重要内容之一。

在研究质点运动时，需要对其运动状态进行描述。

常用的描述方式是采用矢量及其分量进行描述。

矢量是具有大小和方向的物理量，可以用箭头表示。

在描述质点运动时，常用的矢量有位移矢量、速度矢量和加速度矢量。

位移矢量表示质点从初始位置到末位置的位移，可表示为：$vec{s}=vec{r_f}-vec{r_i}$其中，$vec{r_f}$和$vec{r_i}$分别表示末位置和初始位置的位置矢量。

位移矢量的大小为位移的距离，方向为位移的方向。

速度矢量表示质点在某一时刻的速度，可表示为：$vec{v}=frac{Deltavec{r}}{Delta t}$其中，$Deltavec{r}$表示时间间隔内的位移矢量，$Delta t$表示时间间隔。

速度矢量的大小为速度的大小，方向为速度的方向。

加速度矢量表示质点在某一时刻的加速度，可表示为：$vec{a}=frac{Deltavec{v}}{Delta t}$其中，$Deltavec{v}$表示时间间隔内的速度变化量，$Delta t$表示时间间隔。

加速度矢量的大小为加速度的大小，方向为加速度的方向。

矢量分量是将一个矢量沿着不同方向分解为多个分量，常用的矢量分量有$x$分量、$y$分量和$z$分量。

对于位移矢量$vec{s}$，可以将其沿着$x$轴、$y$轴和$z$轴分解为三个分量，分别表示为$s_x$、$s_y$和$s_z$：$s_x=left|vec{s}ight|cdotcostheta_x$$s_y=left|vec{s}ight|cdotcostheta_y$$s_z=left|vec{s}ight|cdotcostheta_z$其中，$theta_x$、$theta_y$和$theta_z$分别表示位移矢量与$x$轴、$y$轴和$z$轴的夹角。

对于速度矢量$vec{v}$和加速度矢量$vec{a}$，同样可以将其沿着$x$轴、$y$轴和$z$轴分解为三个分量，分别表示为$v_x$、$v_y$、$v_z$和$a_x$、$a_y$、$a_z$。

位移和加速度公式一、位移的概念和计算方法1.位移的定义位移是指物体在其中一段时间内从一个位置变化到另一个位置的距离和方向的变化。

它是一个矢量量，具有大小和方向。

2.位移的计算方法如果物体在直线上运动，则位移可以用初始位置和最终位置之间的距离来表示。

设初始位置为qi，最终位置为qf，则位移δq=qf-qi。

如果物体在曲线上运动，则位移需要考虑曲线路径的特性。

通常情况下，我们将其分解为水平方向和垂直方向的位移。

-水平方向的位移计算：将曲线分解为若干小线段，计算每个小线段的水平位移，然后将所有小位移相加。

-垂直方向的位移计算：同样将曲线分解为若干小线段，计算每个小线段的垂直位移，然后将所有小位移相加。

在实际计算中，我们通常使用微积分中的极限概念来计算位移。

通过将曲线分解为无穷小线段，然后使用微积分方法来对每个无穷小位移进行积分，最后将所有无穷小位移的积分结果相加，得到曲线的位移。

二、加速度的概念和计算方法1.加速度的定义加速度是指物体在单位时间内速度的变化率。

它是一个矢量量，是速度的矢量导数。

2.加速度的计算方法加速度可以通过速度和时间的关系来计算。

设物体初始速度为vi，最终速度为vf，时间为t，则加速度a=(vf-vi)/t。

在实际计算中，加速度的计算通常涉及到速度和时间的函数关系。

如果速度是一个常数函数，则加速度为0；但如果速度是一个关于时间的函数，则需要考虑时间的变化对速度的影响，得到加速度的具体数值。

三、位移和加速度的公式1.位移和速度的关系位移和速度之间存在着密切的关系。

根据牛顿第二定律，F=ma，当力作用于物体时，物体将发生加速度变化，从而导致速度的变化。

根据速度的定义，速度是位移对时间的导数，即v=dq/dt。

综上所述，位移与速度之间的关系可以表示为位移等于速度对时间的积分：q=∫v dt。

这个积分公式表示了位移和速度之间的具体关系。

2.位移和加速度的关系根据速度的定义，加速度是速度对时间的导数，即a=dv/dt。

动力学位移与加速度动力学是力学的一个分支，研究物体在受到外力作用下的运动规律。

而在动力学中，位移和加速度是两个重要的概念。

本文将详细讨论动力学位移与加速度的概念、计算方法以及它们之间的关系。

一、动力学位移动力学位移是描述物体在力的作用下从一个位置移动到另一个位置的距离。

它是一个矢量量，可以用于表示物体的移动方向和距离。

在物理学中，位移用符号Δs表示。

计算动力学位移的公式是：Δs = v0t + (1/2)at^2其中，Δs表示位移，v0表示初始速度，t表示时间，a表示加速度。

加速度是指物体单位时间内速度变化的量。

如果物体在运动时速度发生改变，那么它就会受到加速度的影响。

加速度是一个矢量量，它的大小和方向都很重要。

二、动力学加速度动力学加速度是指物体单位时间内速度变化的量。

它表示物体的加速或减速程度。

加速度是一个矢量量，用符号a表示。

计算动力学加速度的公式是：a = (v - v0) / t其中，a表示加速度，v表示末速度，v0表示初始速度，t表示时间。

三、位移与加速度的关系位移和加速度之间存在着一定的关系。

在动力学中，如果已知物体的加速度和时间，就可以通过公式计算出位移；反之，如果已知物体的位移和时间，也可以通过公式计算出加速度。

从位移的计算公式Δs = v0t + (1/2)at^2 中可以看出，位移与加速度成正比。

当加速度增加时，位移也会增加，反之亦然。

这说明了加速度对位移的影响。

从计算加速度的公式a = (v - v0) / t 中可以看出，加速度等于速度的变化量除以时间。

这说明了位移对加速度的影响，因为位移与速度有直接的关系。

如果物体的位移增加，那么速度的变化量也会增加，从而导致加速度增加。

综上所述，动力学位移与加速度是力学中的重要概念，它们描述了物体在受力作用下的运动规律。

位移和加速度之间存在一定的关系，它们相互影响。

通过对位移和加速度的理解和计算，我们能够更好地理解物体的运动特征，为力学问题的分析提供重要的参考依据。

运动学中的速度加速度和位移在运动学中，速度、加速度和位移是三个重要的概念。

它们用来描述物体在运动过程中位置的变化以及运动的特征。

本文将详细介绍速度、加速度和位移的概念及其计算方法，并探讨它们在实际运动中的应用。

一、速度速度是描述物体运动快慢和方向的物理量。

速度的计算公式为速度=位移/时间。

在运动学中，速度可分为瞬时速度和平均速度。

瞬时速度是指物体在某一时刻的瞬时状态；平均速度是指物体在运动过程中的平均状态。

当物体做匀速直线运动时，其速度不变，可以通过物体在某一时间段内的位移与该时间段的时间间隔求得平均速度。

例如，一辆汽车在2小时内行驶了200公里，则它的平均速度为200公里/2小时=100km/h。

二、加速度加速度是描述物体速度变化率的物理量。

加速度的计算公式为加速度=（末速度-初速度）/时间。

正值表示加速度方向与速度方向一致，负值表示方向相反，零值则表示物体运动匀速，加速度没有变化。

在实际运动中，物体的速度往往不是恒定的，因此加速度非常重要。

例如，当我们开车时，踩下油门，车辆会逐渐加速；刹车时，车辆会逐渐减速。

这些都是加速度的体现。

三、位移位移是描述物体位置变化的物理量。

位移的计算公式为位移=末位置-初位置。

位移是一个矢量，既包括大小，也包括方向。

位移与速度和加速度之间存在着密切的关系。

当物体做匀速直线运动时，位移与速度成正比。

例如，一辆车以每小时50公里的速度行驶2小时，其位移为50公里/小时×2小时=100公里。

当物体存在加速度时，位移与加速度之间的关系则更为复杂。

根据牛顿第二定律，加速度等于力对物体的作用力除以物体的质量。

因此，在给定作用力和质量的情况下，加速度越大，物体所产生的位移就越大。

四、运动学中的应用速度、加速度和位移是运动学中常用的概念，并在实际生活中有着广泛的应用。

在交通运输领域，对车辆的速度和加速度进行测量和分析，能够提供重要的交通安全信息。

例如，当知道一辆车的加速度较大时，可以提前采取措施确保行车安全。

动力学中的矢量分析与运动学方程动力学是研究物体运动的力学分支，而矢量分析和运动学方程是动力学中的两个重要概念。

本文将探讨它们的关系和应用。

一、矢量分析在动力学中的应用矢量分析是研究矢量在空间中运动和变化的数学方法。

在动力学中，我们常常需要分析物体的位移、速度和加速度等矢量量，而矢量分析提供了一种有效的工具。

首先，我们来看位移矢量。

位移矢量是描述物体从一个位置到另一个位置的矢量，它的大小等于两个位置之间的直线距离，方向则是从起始位置指向结束位置。

通过矢量分析，我们可以计算出物体在某一时刻的位移，从而了解其位置的变化。

其次，速度矢量是描述物体运动快慢和方向的矢量，它等于位移矢量除以时间间隔。

通过矢量分析，我们可以计算出物体在某一时刻的速度，从而了解其运动状态。

最后，加速度矢量是描述物体运动变化率的矢量，它等于速度矢量的变化率。

通过矢量分析，我们可以计算出物体在某一时刻的加速度，从而了解其运动的加速度变化情况。

总之，矢量分析在动力学中的应用非常广泛，通过对位移、速度和加速度等矢量量的分析，我们可以深入理解物体的运动规律和变化情况。

二、运动学方程的推导和应用运动学方程是描述物体运动规律的数学方程。

在动力学中，我们常常需要通过运动学方程来研究物体的运动状态和变化。

首先，我们来看匀速直线运动的运动学方程。

对于匀速直线运动，物体的位移随时间的变化是线性的，即位移与时间成正比。

因此，我们可以得到匀速直线运动的位移公式：位移等于速度乘以时间。

其次，对于匀加速直线运动，物体的加速度是恒定的，位移随时间的变化是二次函数关系。

通过对位移、速度和加速度的分析，我们可以得到匀加速直线运动的运动学方程：位移等于初速度乘以时间加上加速度乘以时间的平方的一半。

最后，对于曲线运动，物体的运动轨迹是曲线形状的。

通过对曲线的参数方程进行分析，我们可以得到曲线运动的运动学方程。

总之，运动学方程是描述物体运动规律的重要工具，通过对位移、速度和加速度等物理量的分析，我们可以推导出各种运动情况下的运动学方程，从而深入理解物体的运动规律。

物理学中的矢量位移速度与加速度物理学中的矢量位移、速度与加速度物理学是一门研究物质的运动规律和属性的科学。

在物理学中，矢量位移、速度和加速度是三个重要的概念，它们有着密切的联系。

本文将深入剖析这三个概念的定义、计算以及它们之间的关系。

一、矢量位移矢量位移是一个物体从初始位置移动到最终位置的直线距离的有向量表示。

用符号Δr表示，Δr = r2 - r1，其中r2表示物体的最终位置矢量，r1表示物体的初始位置矢量。

二、速度速度是描述物体运动变化率的物理量，它是位移关于时间的导数。

速度的定义是v = Δr / Δt，其中Δr表示位移矢量，Δt表示时间变化的量。

速度是一个矢量量，它既有大小，又有方向。

在国际单位制中，速度单位为米每秒（m/s）。

三、加速度加速度是描述物体速度变化率的物理量，它是速度关于时间的导数。

加速度的定义是a = Δv / Δt，其中Δv表示速度矢量的变化量，Δt表示时间变化的量。

加速度也是一个矢量量，它既有大小，又有方向。

在国际单位制中，加速度单位为米每秒平方（m/s²）。

通过分析位移、速度和加速度的定义，我们可以看出它们之间的关系。

速度是位移的导数，表示单位时间内物体位置的变化率。

而加速度是速度的导数，表示单位时间内速度的变化率。

因此，加速度也可以看作是位移关于时间的二阶导数。

在一维运动中，我们可以用函数的导数来计算速度和加速度。

对于位移函数x(t)，我们可以通过求导得到速度函数v(t)，再次求导得到加速度函数a(t)。

在多维运动中，我们可以将位移、速度和加速度分别看作是矢量的分量，对每个方向进行独立计算。

除了函数法，我们还可以通过图像法来分析位移、速度和加速度之间的关系。

通过绘制位移-时间、速度-时间、加速度-时间的图像，我们可以直观地了解它们的变化规律。

需要特别注意的是，位移、速度和加速度的方向是相对于某个参考点或参考系统而言的。

选择合适的参考点和参考系对于矢量的描述非常重要。

加速运动中的速度、位移和加速度计算1.定义：速度是描述物体运动快慢的物理量，等于物体在单位时间内通过的路程。

2.计算公式：v = s/t，其中v表示速度，s表示路程，t表示时间。

（1）匀速直线运动：速度保持不变。

（2）变速直线运动：速度不断变化。

（3）曲线运动：速度方向时刻变化。

1.定义：位移是描述物体位置变化的物理量，等于物体从初位置到末位置的有向线段。

2.计算公式：Δx = x_f - x_i，其中Δx表示位移，x_f表示末位置，x_i表示初位置。

3.性质：位移是矢量，有大小和方向。

4.定义：加速度是描述物体速度变化快慢的物理量，等于物体速度变化量与时间变化量的比值。

5.计算公式：a = Δv/Δt，其中a表示加速度，Δv表示速度变化量，Δt 表示时间变化量。

6.性质：加速度是矢量，有大小和方向。

四、加速运动1.定义：加速运动是指物体在运动过程中速度不断增加的运动。

（1）匀加速运动：加速度保持不变。

（2）变加速运动：加速度不断变化。

五、计算方法1.运用公式：在已知条件的情况下，运用速度、位移和加速度的计算公式进行计算。

2.画图解：根据物体运动的实际情况，画出速度-时间图、位移-时间图或加速度-时间图，通过图象分析解决问题。

3.运用牛顿运动定律：在涉及外力作用的情况下，运用牛顿运动定律分析物体受力情况，从而解决问题。

六、注意事项1.在计算过程中，注意单位的转换，确保各物理量单位一致。

2.分析物体运动时，注意区分匀速、变速和曲线运动的特点。

3.在解决实际问题时，结合物体运动的实际情况，选择合适的计算方法。

习题及方法：1.习题：一物体做匀速直线运动，速度为2m/s，运动了5秒，求物体通过的路程。

方法：根据速度公式v = s/t，代入已知条件，得到s = v t = 2m/s 5s = 10m。

2.习题：一辆汽车从静止开始加速，加速度为0.5m/s^2，运动了10秒，求汽车的速度。

方法：根据加速度公式a = Δv/Δt，代入已知条件，得到Δv = aΔt = 0.5m/s^210s = 5m/s。

《大学物理学C 》课程基本内容第一章 质点的运动1．直角坐标系、极坐标系、自然坐标系※2．质点运动的描述：位置矢量r 、位移矢量r ∆=)()(t r t t r-∆+、运动方程)(t r r =。

在直角坐标系中,k t z j t y i t x t r)()()()(++=速度：t rv d d=； 加速度：22d d d d t r t v a == 在直角坐标系中，速度k v j v i v v z y x ++=,加速度k a j a i a a z y x++=自然坐标系中，速度 τ v v =＝τts d d ，加速度t n a a a +==n r v t v 2d d +τ 在极坐标系中,角量的描述：角速度t d d θω=，角加速度22d d d d t t θωα==3．运动学的两类基本问题：第一类问题:已知运动方程求速度、加速度等。

此类问题的基本解法是根据各量定义求导数。

第二类问题:已知速度函数(或加速度函数)及初始条件求运动方程。

此类问题的基本解法是根据各量之间的关系求积分。

例如据txv d d =，可写出积分式⎰x d ＝⎰t v d .由此求出运动方程)(t x x =。

4．相对运动：位移:t u r r ∆+'∆=∆ ，速度：u v v+'=,加速度：0a a a +'=第七章 气体动理论1．对“物质的微观模型”的认识；对“理想气体”的理解。

※2．理想气体的压强公式23132v n p k ρε==，其中221v m k =ε※理想气体物态方程：RT MmpV =或 nkT p =理解压强与微观什么有关，即压强的物理含义是什么.※3．理想气体分子的平均平动动能与温度的关系：kT k 23=ε 理解温度与微观什么有关，即温度的物理含义。

※4．能量均分定理：气体处于平衡态时，分子每个自由度上的平均能量均为2kT概念：自由度※理想气体内能公式：RT iM m E 2=5．麦克斯韦气体分子速率分布律 ※麦克斯韦气体分子速率分布函数：定义：vNN v f d d 1)(=函数：22232π2π4)(v v v kTm ekT m f -⎪⎭⎫⎝⎛= 以及v v f NNd )(d =；v v Nf N d )(d =；⎰21d )(v v v v Nf ；⎰21d )(v v v v f 等表示的物理含义。