第1章++1.2++加速度矢量的表示
- 格式:ppt
- 大小:1.53 MB
- 文档页数:51




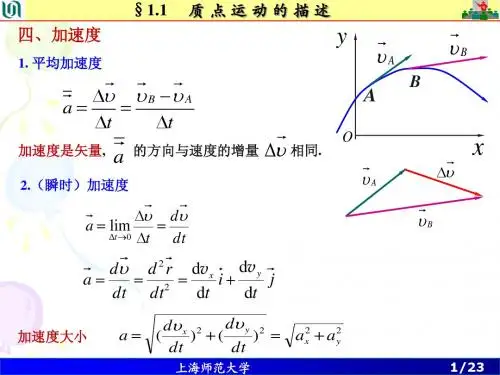

第一章 运动的描述第4节速度变化快慢的描述——加速度一、加速度1.定义:速度的改变量与发生这一改变所用时间的比值,通常用a 表示。
2.表达式:a =ΔvΔt 。
3.矢量性加速度既有大小,又有方向,是矢量。
由a =ΔvΔt 可知,加速度a 的方向与速度变化量Δv 的方向相同。
4.单位在国际单位制中,加速度的单位是米每二次方秒,符号m/s 2或m·s -2。
5.物理意义加速度是描述物体运动速度变化快慢的物理量。
二、加速度方向与速度方向的关系1.如图1-4-1所示,取初速度v 0的方向为正方向:对于加速运动,有v t >v 0,即Δv >0,此时a >0,表示加速度的方向与速度的方向相同,如图甲所示。
图1-4-12.对于减速运动,有v t <v 0,即Δv <0,此时a <0,表示加速度的方向与速度的方向相反,如图乙所示。
三、从v -t 图像看加速度1.通过速度—时间(v -t )图像不但能够了解物体运动的速度随时间变化的规律,还能够知道物体的加速度。
2.从速度—时间图线的倾斜程度大小就能判断加速度的大小,倾斜程度越大,加速度越大。
1.自主思考——判一判(1)如果速度很大,则加速度一定很大。
(×) (2)如果速度变化量很大,则加速度一定很大。
(×)(3)加速度是矢量,它的方向与速度变化量的方向一致。
(√)(4)物体的速度为零,加速度也为零。
(×)(5)取初速度方向为正方向时,加速度为正值时,物体做加速运动。
(√)(6)物体的v-t图像是一条倾斜直线时,物体运动的加速度是恒定的。
(√)2.合作探究——议一议(1)直线运动中,加速度的正负表示什么含义?加速度为负值,物体就一定做减速运动吗?[提示]①加速度的正、负表示与规定的正方向是同向还是反向。
②不一定。
加速度为负值,若速度为正值,则物体减速;若速度也为负值,则物体加速。


§2、速度、加速度的分量表达式上一次课,我们为了将运动的一些特征能直接的表示出来,而定义了速度和加速度,22;dt r d dt v d a dt r d v =≡≡ 。
在一般情况下它们往往都是时间t 的函数。
何谓定义呢?定义它本身不是可以用什么方法或者数学手段加以证明得到的,而是根据实际需要常常用到而定义下来的名称和概念。
例如过两点成一条直线……。
由于速度和加速度都是矢量,因此都可以将它们表示成分量的形式。
这次课将准备讨论速度、加速度在各种坐标系中的表达式。
一、 直角坐标系——直角坐标系又称笛卡儿坐标系在直角坐标系中,质点的位置矢径可以写成为:........z k y j x i r ++= (1)根据速度的定义可知dtr d v ≡将(1)代入,则有 1、速度: z y x v k v j v i dt dz k dt dy j dt dx i z k y j x i dt d dt r d v ++=++=++==...........................................)(于是,我们比较上面的等式,就可得到速度在直角坐标系中的分量表达式为:z dtdz v y dt dy v x dt dx v z y x ======;;可见速度沿三直角坐标轴的分量(即分速度)就等于其相应的坐标对时间t 的一阶导数。
速度的大小:222z y x v v v v v ++== 速度的方向就用方向余弦来表示:vv k v v v j v v v i v z y y ===),cos(;),cos(;),cos( 。
同理,我们由加速度的定义不难得到它的分量表达式。
2、加速度根据加速度的定义:zy x z y x a k a j a i dt dv k dt dv j dt dv i dt z d k y d j x d i dt dz k dy j dx i dt d dt v d a ++=++=++=++==2222)(比较这些恒等式可得加速度的直角坐标分量表达式:z dt z d v dv a y dt y d v dt dv a x dtx d v dt dv a z t z y y y x x x ============222222 于是可得加速度的大小为:222z y x a a a a a ++== 加速度的方向用方向余弦表示。

第一章 质点运动学和牛顿运动定律1.1平均速度 v =t△△r1.2 瞬时速度 v=lim 0△t →△t △r =dt dr1. 3速度v=dtds==→→lim lim△t 0△t △t△r 1.6 平均加速度a =△t△v1.7瞬时加速度(加速度)a=lim 0△t →△t△v =dt dv1.8瞬时加速度a=dt dv =22dt rd1.11匀速直线运动质点坐标x=x 0+vt 1.12变速运动速度 v=v 0+at 1.13变速运动质点坐标x=x 0+v 0t+21at 21.14速度随坐标变化公式:v 2-v 02=2a(x-x 0) 1.15自由落体运动 1.16竖直上抛运动⎪⎩⎪⎨⎧===gy v at y gtv 22122 ⎪⎪⎩⎪⎪⎨⎧-=-=-=gy v v gt t v y gt v v 221202200 1.17 抛体运动速度分量⎩⎨⎧-==gt a v v av v yx sin cos 001.18 抛体运动距离分量⎪⎩⎪⎨⎧-•=•=20021sin cos gt t a v y t a v x1.19射程 X=g av 2sin 21.20射高Y=gav 22sin 201.21飞行时间y=xtga —ggx 21.22轨迹方程y=xtga —av gx 2202cos 2 1.23向心加速度 a=Rv 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =Rv 21.27切向加速度只改变速度的大小a t =dtdv1.28 ωΦR dtd R dt ds v ===1.29角速度 dtφωd =1.30角加速度 22dt dtd d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR R R R v == a t =αωR dtd R dt dv ==牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。

第一章 质点运动学和牛顿运动定律1.1平均速度 v =t△△r1.2 瞬时速度 v=lim△t →△t △r =dtdr1. 3速度v=dtds ==→→lim lim△t 0△t △t△r 1.6 平均加速度a =△t△v1.7瞬时加速度(加速度)a=lim△t →△t △v =dtdv1.8瞬时加速度a=dt dv =22dtrd1.11匀速直线运动质点坐标x=x 0+vt 1.12变速运动速度 v=v 0+at 1.13变速运动质点坐标x=x 0+v 0t+21at 21.14速度随坐标变化公式:v 2-v 02=2a(x-x 0) 1.15自由落体运动 1.16竖直上抛运动⎪⎩⎪⎨⎧===gy v at y gtv 22122 ⎪⎪⎩⎪⎪⎨⎧-=-=-=gy v v gt t v y gt v v 221202200 1.17 抛体运动速度分量⎩⎨⎧-==gta v v av v y x sin cos 001.18 抛体运动距离分量⎪⎩⎪⎨⎧-∙=∙=20021sin cos gt t a v y t a v x1.19射程 X=g av 2sin 21.20射高Y=gav 22sin 201.21飞行时间y=xtga —g gx 21.22轨迹方程y=xtga —av gx 2202cos 2 1.23向心加速度 a=Rv 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =Rv 21.27切向加速度只改变速度的大小a t =dtdv1.28 ωΦR dtd R dt ds v ===1.29角速度 dtφωd =1.30角加速度 22dt dtd d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR RR R v == a t =αωR dt d R dt dv ==牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。

第2课时:匀变速直线运动的规律及其应用读基础知识基础回顾:一、匀变速直线运动的规律1.匀变速直线运动沿一条直线且加速度不变的运动.2.匀变速直线运动的基本规律(1)速度公式:v=v0+at.(2)位移公式:x=v0t+12at2.(3)位移速度关系式:v2-v02=2ax.二、匀变速直线运动的推论1.三个推论(1)连续相等的相邻时间间隔T内的位移差相等.即x2-x1=x3-x2=…=x n-x n-1=aT2.(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初、末时刻速度矢量和的一半,还等于中间时刻的瞬时速度.平均速度公式:v=v0+v2=2v t.(3)位移中点速度2xv=v02+v22.2.初速度为零的匀加速直线运动的四个重要推论(1)T末、2T末、3T末、…、nT末的瞬时速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.(2)T内、2T内、3T内、…、nT内的位移之比为x1∶x2∶x3∶…∶x n=12∶22∶32∶…∶n2.(3)第1个T内、第2个T内、第3个T内、…、第n个T内的位移之比为xⅠ∶xⅡ∶xⅢ∶…∶x N=1∶3∶5∶…∶(2n-1).(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶t n=1∶(2-1)∶(3-2)∶(2-3)∶…∶(n-n-1).自查自纠:(1)匀变速直线运动是加速度均匀变化的运动。
()(2)匀变速直线运动是速度均匀变化的运动。
()(3)匀加速直线运动的位移是均匀增大的。
()(4)某物体从静止开始做匀加速直线运动,速度由0到v运动距离是由v到2v运动距离的2倍。
() (5)对任意直线运动,其中间时刻的瞬时速度一定等于其平均速度。
()(6)在匀变速直线运动中,中间时刻的速度一定小于该段时间内位移中点的速度。
()答案(1)×(2)√(3)×(4)×(5)×(6)√研考纲考题要点1匀变速直线运动规律的基本应用1.匀变速直线运动公式为矢量式,一般规定初速度v0的方向为正方向(当v0=0时,一般以加速度a的方向为正方向),与正方向同向的物理量取正值,反向的物理量取负值。
加速度的矢量关系加速度的矢量关系加速度是物体在单位时间内速度变化的量度,是一个矢量量。
在物理学中,加速度的矢量关系是非常重要的一个概念。
在本文中,我们将探讨加速度的矢量关系及其应用。
加速度的定义加速度是物体在单位时间内速度变化的量度,是一个矢量量。
加速度的单位是米每秒平方(m/s²)。
加速度的方向与速度变化的方向相同,即加速度的方向与物体的运动方向一致。
加速度的矢量关系加速度是一个矢量量,它有大小和方向。
加速度的大小等于速度变化量与时间的比值,即a = Δv/Δt。
加速度的方向与速度变化的方向相同。
加速度的矢量关系可以用矢量图表示。
在矢量图中,加速度的大小用矢量的长度表示,加速度的方向用矢量的方向表示。
矢量图中,加速度的起点为物体的初始速度,终点为物体的末速度。
应用加速度的矢量关系在物理学中有广泛的应用。
以下是一些常见的应用:1. 运动学分析在运动学分析中,加速度的矢量关系可以用来计算物体的运动轨迹和速度变化。
例如,在自由落体运动中,物体的加速度为9.8m/s²,可以用来计算物体的下落时间和下落距离。
2. 力学分析在力学分析中,加速度的矢量关系可以用来计算物体所受的力和反作用力。
例如,在牛顿第二定律中,加速度与物体所受的力成正比,可以用来计算物体所受的力。
3. 工程应用在工程应用中,加速度的矢量关系可以用来设计机械和结构。
例如,在汽车设计中,加速度的矢量关系可以用来计算汽车的加速度和制动距离。
总结加速度的矢量关系是物理学中非常重要的一个概念。
加速度是一个矢量量,它有大小和方向。
加速度的矢量关系可以用来计算物体的运动轨迹和速度变化,计算物体所受的力和反作用力,以及设计机械和结构。
加速度的矢量关系在物理学和工程应用中有广泛的应用。