28.1锐角三角函数(第二课时)-2014届

斜边c对边abC B A28．1锐角三角函数（2） 余弦、正切学案一．知识巩固。

（每个题目5分，合计20分）1、在Rt △ABC 中，∠C=90°，当锐角A 确定时， ∠A 的对边与斜边的比是 ，2、 在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D 。

已知AC= 5 ，BC=2，那么sin ∠ACD ＝（ ）A ．53B ．23C ．255D ．523、 如图，在Rt △ABC 中，∠C=90°，求sinA 和sinB 的值．4、在 90,=∠∆C ABC Rt 中，若将各边长度都扩大为原来的2倍，则 ∠A 的正弦值 （ ） A ．扩大2倍 B ．缩小2倍 C ．扩大4倍 D ．不变二．新知探究。

（每个题目10分，合计100分）1、类似于正弦的情况， 如图在Rt △BC 中，∠C=90°，当锐角A 的大小确定时，∠A 的邻边与斜边的比、∠A 的对边与邻边的比也分别是 ．我们 把∠A 的邻边与斜边的比叫做∠A 的 ，记作 ；把∠A 的对边与邻边的比叫做∠A 的 ，记作 。

2、当∠A=30°时，我们有cosA=cos30°=； 当∠A=45°时，我们有tanA=tan45°= ．(1)CB A436CB A判断题 4、cos x =21=60°． （ ）5、α是锐角，且sin α=23，则α=30°． （ ）6、cos45°－cos15°=cos30°=23． （ ）7、若α为锐角，则2)1(cos -α=cos α－1．（ ） 8、若A 为锐角则0＜sin A ＜1，0＜cos A ＜1． （ ） 9、 若a 为锐角，则sin a +cos a ＞1． （ ） 10、已知:Rt △ABC 中,∠C=90°,cosA=35,AB=15,则AC 的长是( ).A.3B.6C.9D.12三．运用提高。

28.1 锐角三角函数（第二课时）一、【教材分析 】1、了解锐角三角函数的概念，能够正确应用 、cosA 、tanA 表示知识 sinA直角三角形中两边的比．目标2、逐步培养学生观察、比较、分析、概括的思维能力．教 能力通过锐角三角函数的学习，进一步认识函数，体会函数的变化与对学 目标 应的思想，逐步培养学生会观察、比较、分析、概括等逻辑思维能力． 目情感引导学生探索、发现，以培养学生独立思考、勇于创新的精神和良标目标 好的学习习惯．教学 理解余弦、正切的概念．重点教学 熟练运用锐角三角函数的概念进行有关计算．难点二、【教学流程 】教学 教学问题设计环节【问题 】在 Rt △ ABC 中， ∠C=90 °Bca 情 AbC锐角正弦的定义1.师生活动 二次备课复习引入，巩固旧知识的同时，为新知识作准备 .∠ A 的正弦：景 创2. 当锐角 A 确定时，∠ A 的邻边设与斜边的比， ∠ A 的对边与邻边的比也随之确定吗？为什么？交流并说出理由。

sinA ＝A 的对边 aA 的斜边 c【探究 1】 教师类比正弦的情况提出问题，1. 在 Rt △ ABC 和 Rt △ A ’B ’C 中’ 引导学生利用相似三角形的知识∠ C ＝∠ C ’＝ 90°，∠ A ＝∠ A ’ 进行论证（请学生自己完成证明）那么 AC 与 A 'C ' 有什么关系． 结论： 在直角三角形中，当锐角ABA 'B 'B 的度数一定时，不管三角形的你能解释一下吗？大小如何，∠B的邻边与斜边的比也是一个固定值.∵∠ C=∠ C’ =90 o，∠A=∠ A ，自’∴Rt△ ABC∽ Rt△A B C ，’ ’ ’主∴ AC AB ，探A'C' A' B'究即 AC A'C 'AB A' B'【探究 2】2.类似于前面的推理情况 ,如图在Rt△ ABC 中，∠ C=90°，当锐角 A 的大小确定时，∠A的邻边与斜边的比是定值，∠A 的对边与邻边的比也是确定的吗？3. sin A A的对边 a斜边 ccos A A的邻边b 斜边 ctan A A的对边aA的邻边b教师继续给出直角三角形的边与边的比值假设，每一位学生参与到问题情境的探究中去，通过类比的方式熟练推理论证 .教师点拨、指导、总结出余弦和正切的概念，同时探究出锐角三角函数的定义 .如图，在Rt△ ABC 中，∠ C＝90°，我们把∠ A 的邻边与斜边的比叫做∠ A 的余弦（ cosine），记作cosA，即cos A A的邻边 b斜边 c我们把∠ A 的对边与邻边的比叫做∠ A 的正切（ tangent），记作tanA，即tan AA的对边 aA的邻边 b∠A 的正弦、余弦、正切都叫做∠A 的锐角三角函数.尝试应用1如图，在 Rt△ABC 中，∠ C 教师提出问题＝ 90°，BC =6，AB=10，求 sinA，学生独立思考解答对教材知识cosA, tanA 的值 . B 分析：通过勾股定理求解出未知的加固10边 AC 的长，根据正弦，余弦，6 正切的概念求出相应的答案 .解：由勾股定理得A CAC AB2BC2102628因此sin ABC6 3 2、下图中∠ ACB =90°， CD ⊥ AB 10 5AB, 垂足为 D. 指出∠ A 和∠ B 的AC 84对边、邻边 .cos A10 5AB DBBC 6 3tan A84AC强 化 学 生 对几 何 图 形 的认识和变通ACtan ACD总 结 做 题 规ACCD tan BBC律1、如图 ,在 Rt △ ABC 中 ,锐角 A对 内 容 的 升 的 邻 边 和 斜 边 同 时 扩 大 100 教师与学生共同归纳总结锐角三 华理解认识倍 ,tanA 的值（ ） 角函数运用规律。

锐角三角函数第二课时教案标题：锐角三角函数第二课时教案正文：一、教学目标通过本课时的学习，学生应能够：1. 理解锐角三角函数的定义及其在平面几何中的应用；2. 熟练计算锐角三角函数的数值，并能运用这些数值解决相关问题；3. 掌握如何绘制锐角的三角函数图像；4. 培养学生的逻辑思维和问题解决能力。

二、教学重点1. 锐角三角函数的概念和定义；2. 锐角三角函数的性质及其应用。

三、教学难点1. 锐角三角函数图像的绘制；2. 锐角三角函数的应用题解决方法。

四、教学过程1. 导入教师通过问题情境或实例引导学生思考，在直角三角函数的基础上，如何推导出锐角三角函数的定义。

2. 知识讲解2.1 锐角三角函数的定义a) 引入正弦、余弦、正切的定义，解释它们在锐角情境下对应的数学意义；b) 讲解正弦函数和余弦函数的定义：在锐角三角形中，正弦函数（sin）等于对边与斜边的比值，余弦函数（cos）等于邻边与斜边的比值；c) 讲解正切函数的定义：在锐角三角形中，正切函数（tan）等于对边与邻边的比值。

2.2 锐角三角函数的性质及应用a) 探究锐角三角函数的周期性、奇偶性；b) 讲解角度与弧度的转换关系；c) 结合具体问题和实例，展示锐角三角函数在平面几何中的应用。

3. 计算练习教师设计一些计算题目，引导学生进行计算练习，熟悉锐角三角函数的计算方法。

4. 图像绘制4.1 正弦函数和余弦函数的图像绘制a) 提供正弦函数和余弦函数的表格，并鼓励学生通过计算和绘制找出规律；b) 讲解如何绘制正弦函数和余弦函数的图像，强调振幅、周期和相位差的概念。

4.2 正切函数的图像绘制a) 提供正切函数的表格，并鼓励学生通过计算和绘制找出规律；b) 讲解如何绘制正切函数的图像，强调渐近线和周期的概念。

5. 应用问题解析教师提供一些有关锐角三角函数的实际问题，引导学生通过绘制函数图像和计算来解决这些问题，培养学生的问题解决能力。

6. 小结与作业布置对本课时的重点知识进行总结，并布置相关的作业。

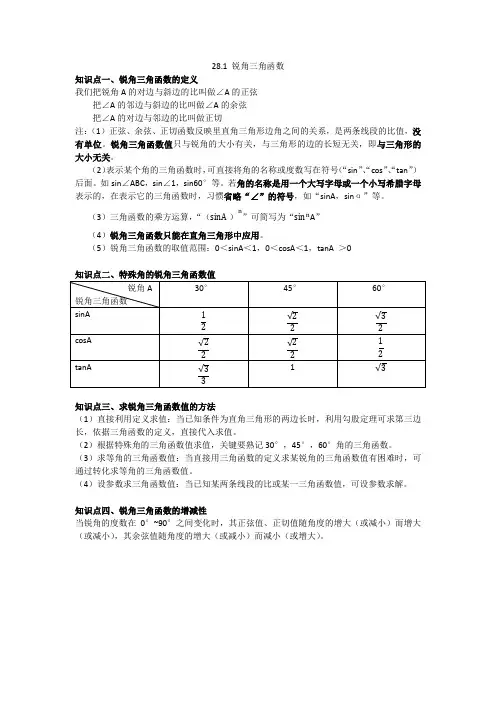
28.1 锐角三角函数知识点一、锐角三角函数的定义我们把锐角A的对边与斜边的比叫做∠A的正弦把∠A的邻边与斜边的比叫做∠A的余弦把∠A的对边与邻边的比叫做正切注：（1）正弦、余弦、正切函数反映里直角三角形边角之间的关系，是两条线段的比值，没有单位。

锐角三角函数值只与锐角的大小有关，与三角形的边的长短无关，即与三角形的大小无关。

（2）表示某个角的三角函数时，可直接将角的名称或度数写在符号（“sin”、“cos”、“tan”）后面。

如sin∠ABC，sin∠1，sin60°等。

若角的名称是用一个大写字母或一个小写希腊字母表示的，在表示它的三角函数时，习惯省略“∠”的符号，如“sinA，sinα”等。

（3）三角函数的乘方运算，“（sinA ）n”可简写为“sin n A”（4）锐角三角函数只能在直角三角形中应用。

（5）锐角三角函数的取值范围：0＜sinA＜1，0＜cosA＜1，tanA ＞0知识点三、求锐角三角函数值的方法（1）直接利用定义求值：当已知条件为直角三角形的两边长时，利用勾股定理可求第三边长，依据三角函数的定义，直接代入求值。

（2）根据特殊角的三角函数值求值，关键要熟记30°，45°，60°角的三角函数。

（3）求等角的三角函数值：当直接用三角函数的定义求某锐角的三角函数值有困难时，可通过转化求等角的三角函数值。

（4）设参数求三角函数值：当已知某两条线段的比或某一三角函数值，可设参数求解。

知识点四、锐角三角函数的增减性当锐角的度数在0°~90°之间变化时，其正弦值、正切值随角度的增大（或减小）而增大（或减小），其余弦值随角度的增大（或减小）而减小（或增大）。

28.1 锐角三角函数第二课时(刘佳)一、教学目标1．核心素养:通过锐角三角函数---余弦、正切的学习||，初步形成基本的几何直观、运算能力、推理能力. 2．学习目标（1）1.1.1理解余弦、正切及锐角三角函数的概念（2）1.1.2能熟练运用锐角三角函数的概念进行有关计算（3）1.1.3理解并掌握互余两角三角函数间的关系（4）1.1.4理解并掌握同角三角函数间关系3．学习重点熟练运用锐角三角函数的概念进行有关计算4．学习难点互余两角和同角的三角函数关系二、教学设计（一）课前设计1．预习任务任务1 阅读教材P64-P65||，思考：什么是余弦？任务2 阅读教材P64-P65||，思考：什么是正切？2．预习自测一、选择题1．如图||，在Rt△ABC中||，CD是斜边AB上的中线||，若CD＝5||，AC＝6||，则cos B的值是()A.34 B.35 C.43D. 45答案： D解析：Rt △ABC 中||，CD 是斜边AB 上的中线||，所以CD ＝AD ＝BD ＝5||，所以AB ＝10||，因为AC ＝6||，据勾股定理可得BC ＝8||，所以cos B ＝45.故选D. 2.在Rt △ABC 中||，5sin 13C 90A ∠==o ，||，则tan B 的值为（ ） A.1213 B.512 C.1312 D.125答案：D解析：Rt △ABC 中||，设a ＝x 5||，则x c 13=||，x b 12=||，所以tan B 512=.故选D.3.在Rt △ABC 中||，ACB 90∠=o ||，CD 是斜边AB 上的高||，8,15BC AC ==||，设BCD α∠=||，则cos α的值为（ ） A.87B.78C.817D.1517答案：D解析：据勾股定理可知||，AB 17=||，ABC 111581722CD S ∆=⨯⨯=⨯⨯，所以17120=CD ||，所以cos α1517=.故选D. （二）课堂设计 1．知识回顾（1）正弦的概念：在Rt △ABC 中||，∠C=90°||，我们把锐角A 的对边与斜边的比叫做∠A 的正弦||，即ABBCA A =∠=斜边的对边sin .（2）函数的概念：设在某变化过程中有两个变量x 、y||，如果对于x 在某一范围内的每一个确定的值||，y 都有唯一确定的值与它对应||，那么就称y 是x 的函数||，x 叫做自变量. （3）勾股定理：在直角三角形中||，两直角边的平方和等于斜边的平方． 2．问题探究问题探究一●活动一 类比正弦||，得出结论复习思考：在Rt △ABC 中||，∠C=90o ||，当锐角A 确定时||，不管三角形的大小如何||，∠A 的对边与斜边的比就随之确定.此时||，其他边之间的比是否也确定了呢？如图：Rt △ABC 与Rt △A ´B ´C ´||，∠C=∠C ´=90o||，∠A=∠A ´=α||，那么AC AB 与''''AC A B 、BCAC与''''B C AC有什么关系？ 分析：由于∠C=∠C ´=90o ||，∠A=∠A ´=α||，所以Rt △ABC ∽Rt △A ´B ´C ´||，则''''AC ABAC A B=||，即''''AC AC AB A B =同理||，''''BC B C AC AC=结论：在直角三角形中||，当锐角A 的大小确定时||，∠A 的邻边与斜边的比、∠A 的对边与邻边的比也分别是确定的.我们把锐角A 的邻边与斜边的比叫做∠A 的余弦||，记作 cosA||，即cosA ＝＝bc把∠A 的对边与邻边的比叫做∠A 的正切.记作tanA||，即tanA ＝＝a b●活动二 函数思想||，理论提升 思考：sinA 是A 的函数吗？分析：对于锐角A 的每一个确定的值||，sinA 有唯一确定的值与它对应||，所以sinA 是A 的函数.同理||，cosA 、tanA 也是A 的函数.定义：锐角A 的正弦||，余弦||，正切都叫做∠A 的锐角三角函数. 问题探究二●活动一初步运用||，简单求值例1.如图||，在Rt △ABC 中||，∠C=90°||，BC=6||，sinA=35||，求cosA 、tanB 的值．【知识点：三角函数概念||，勾股定理；数学思想：数形结合】 详解：Q sinA=BC AB =35||，BC=6||，∴AB=5610sin 3BC A =⨯= C ´´C BB ´A又22AB BC -22106-，∴cosA=AC AB =45||，tanB=AC BC =43. 点拨：在直角三角形中||，只要已知任意两条边、或者一边和一锐角三角函数||，都可根据勾股定理求出第三边||，进而求出所有锐角三角函数值．例2.如图||，在△ABC 中||， AD ⊥BC||，垂足是D||，BC ＝14||，AD ＝12||，tan ∠BAD ＝34||，求sinC 的值．【知识点：三角函数概念||，勾股定理；数学思想：数形结合】 详解：∵AD ⊥BC||，∴tan ∠BAD ＝BDAD .∵tan ∠BAD ＝34||，AD ＝12||，∴34＝BD12.∴BD ＝9. ∴CD ＝BC －BD ＝14－9＝5.∴在Rt △ADC 中||，AC ＝AD 2＋CD 2＝122＋52＝13. ∴sin C ＝AD AC ＝1213.点拨：在求解直角三角形的问题中||，三角函数是解题的突破口||，由已知三角函数求得相应线段长||，进而求出未知三角函数．问题探究三 互余两角的三角函数之间有什么关系？重点、难点知识★▲●活动一观察思考||，归纳总结互余两角之间的三角函数有怎样的关系呢？如图||，在Rt △ABC 中||，∠C ＝90°．=A sin ()()||，()()=B cos ||，则B A cos ____sin ； B sin ＝()()||，=A cos ()()||，则A cos ____B sin ； A tan ＝()()||，B tan ＝()()||，则____tan tan =⋅B A ． 归纳结论：若βα、为锐角||，且090=+βα||，则___sin =α||，___sin =β||，___tan tan =⋅βα. 问题探究四 同角的三角函数之间有什么关系？重点、难点知识★▲●活动一观察思考||，归纳总结 同角三角函数间有怎样的关系呢？ 如图||，在Rt △ABC 中||，∠C ＝90°．归纳结论：若0°<α<90°||，则①平方关系：1cos sin 22=+αα；②弦切关系：αααcos sin tan =． 3．课堂总结【知识梳理】（1）在Rt △ABC 中||，∠C=90°||，我们把锐角A 的邻边与斜边的比叫做∠A 的余弦||，记作cosA=b c ；把锐角A 的对边与邻边的比叫做∠A 的正切||，记作tanA=a b.（2）锐角A 的正弦||，余弦||，正切都叫做∠A 的锐角三角函数. （3）若90A B ∠+∠=o ||，则sin A =cos B ||，sin B =cos A （4）22sin cos 1A A +=||，sin tan cos AA A=【重难点突破】（1）求解三角函数基本计算||，找准角的对边、邻边是关键.（2）在求解三角函数问题时||，要灵活运用公式||，将求一个锐角的三角函数问题转化成求另外一个角的三角函数或这个角的其他三角函数. 4．随堂检测 一、选择题1.在直角三角形中||，各边的长度都扩大5倍||，则锐角A 的三角函数值（ ）A.也扩大3倍B.缩小为原来的15C.都不变D.有的扩大||，有的缩小 答案： C解析：∠A 、∠B 、∠C 所对应的边分别为a 、b 、c||，sinB=b/a||，当该直角三角形的各边长都扩大5倍后||，sinB=5b/5a=b/a||，所以答案为C. 【知识点：三角函数概念】2．在ABC ∆Rt 中||，︒=∠90C ||，如果4=AB ||，2=BC ||，则B cos 等于（ ）A ．12 B ．2 C ．2D ．1 答案：A解析：在ABC ∆Rt 中||，B cos 21==AB BC .故选A. 【知识点：三角函数概念||，勾股定理；数学思想：数形结合】3．在△ABC 中||，AB=5||，BC=6||，B 为锐角且sinB=35||，则∠C 的正切值等于（ ）A ．56B ．32CD 答案：B解析：过A 作AD ⊥BC 于D||，在Rt △ABD 中||，因为B 为锐角且sinB=35||，所以AD=3||，据勾股定理可得：BD=4||，所以DC=2||，tanC 23==DC AD .故选B. 【知识点：三角函数概念||，勾股定理；数学思想：数形结合】 二、填空题4.sin 259°+sin 231°的值是_______. 答案：1解析：sin 259°+sin 231°= sin 259°+cos 259°=1 【知识点：同角与互余两角的三角函数】5.在ABC ∆中||，90C ∠=o ||，2sin 5A =||，则cos A =______||，sinB =______||，tan A =______.答案：521 、521 、21212 解析：设AB 2125===AC CB ，，则||，所以cos A =521||，sin B=521||，tan A =21212.【知识点：三角函数概念||，勾股定理】。