电阻 电感 电容的并联电路

rlc串并联电路所有公式(二)RLC串联电路公式1. 电抗的计算公式•电感的电抗（XL）计算公式为：XL = 2πfL，其中f为频率，L 为电感值。

例如，有一个电感值为10mH的电感元件，频率为1kHz，则其电抗为：XL = 2 * * 1000 * = Ω•电容的电抗（XC）计算公式为：XC = 1 / (2πfC)，其中f为频率，C为电容值。

例如，有一个电容值为100nF的电容元件，频率为10kHz，则其电抗为：XC = 1 / (2 * * 10000 * ) = Ω2. 线路总阻抗的计算公式•电感与电容并联时，总阻抗（Z）的计算公式为：Z = √((R^2 + (XL - XC)^2))，其中R为电阻值，XL为电感的电抗，XC为电容的电抗。

例如，一个RLC串联电路中，有一个10Ω的电阻、100mH的电感和100nF的电容，并且频率为1kHz。

先计算电感的电抗：XL = 2 * * 1000 * = Ω再计算电容的电抗：XC = 1 / (2 * * 1000 * ) = Ω最后计算总阻抗：Z = √((10^2 + ( - )^2)) = Ω3. 相位角的计算公式•电感与电容并联时，总阻抗（Z）与电感的相位角（θ）的计算公式为：θ = arctan((XL - XC) / R)例如，继续以上例子，计算相位角：θ = arctan(( - ) / 10) = °RLC并联电路公式1. 电抗的计算公式•电感的电抗（XL）计算公式为：XL = 2πfL，其中f为频率，L 为电感值。

例如，有一个电感值为10mH的电感元件，频率为1kHz，则其电抗为：XL = 2 * * 1000 * = Ω•电容的电抗（XC）计算公式为：XC = 1 / (2πfC)，其中f为频率，C为电容值。

例如，有一个电容值为100nF的电容元件，频率为10kHz，则其电抗为：XC = 1 / (2 * * 10000 * ) = Ω2. 线路总导纳的计算公式•电感与电容串联时，总导纳（Y）的计算公式为：Y = √((G^2 + (BL - BC)^2))，其中G为导纳（倒数阻抗）值，BL为电感的电抗，BC为电容的电抗。

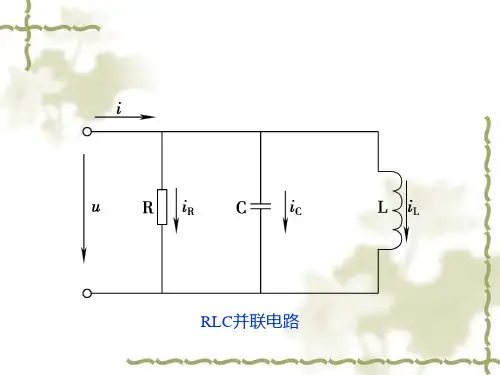
电阻、电感和电容并联电路3.6.1 电压和电流的关系如图3.17（a ）为RLC 并联电路，3.17（b ）是它的相量图。

按图中选取的电流、电压关联参考方向，并设电压为 )sin(2u t U u ψω+= （3-31）（a ） （b ）图3.17 RLC 并联电路及相量图则根据KCL 可写出L C R i i i i ++= （3-32）用相量表示式（3-33）（3-34）为u U U ψ∠=. （3-33）L C R I I I I ....++= （3-34）根据各元件的电压电流的相量关系，式（3-34）可改写成 ......)1(11U Y U C L j R Cj UL j UR U I =⎥⎦⎤⎢⎣⎡+-+=++=ωωωω（3-35） 式（3-35）也称为欧姆定律的相量形式，复数Y 称为复导纳。

由相量图可知22)(L C R I I I I -+= （3-36） RL C I I I -=arctanϕ （3-37） 3.6.2 复导纳 由式（3-35）可知RLC 并联电路的复导纳为 jB G B B j G LC j R Y L C +=-+=++=)()1(1ωω （3-38） 或 ϕ∠==Y U IY .. （3-39）式中，Y 称为电路的复导纳，单位是西门子（S ）。

实部G 是该电路的电导，单位西门子（S ），虚部L C B B B L C ωω1-=-=称为电纳，单位西门子（S ），其中22B G Y +=为复导纳Y 的模，也称为导纳，⎪⎪⎭⎫ ⎝⎛-==G B B G BL C arctan arctan ϕ为复导纳的辐角，也称为导纳角。

3.6.3电路中的三种情况及相量图电路元件参数的不同，电路所呈现的状态不同。

对RLC 并联电路可分为下列三种情况。

1.当C L B B >，即C L I I >，0<ϕ，表明总电流滞后电压，电路呈感性的，如图 3.18（a ）所示2.当C L B B <，即C L I I <，0<ϕ，表明总电流超前电压，电路呈容性，如图3.18（b ）所示3.当C L B B =，即C L I I =，0=ϕ表明电端口电压与电流同相，电路呈阻性的，这种情况称为RLC 并联电路的谐振，如图3.18（c ）所示（a ） （b ） （c ）图3.18 RLC 并联电路三种情况相量图[例3.11] 在RLC 的并联电路中，已知F C mH L R μ40,5020==Ω=，，当该电路接入220V 、50Hz 的正弦电源时，求电路的复导纳为多少？写出电路中总电流的瞬时表达式。

电感和电容并联的等效阻抗
电感和电容并联的等效阻抗是指将电感和电容并联后所产生的
电阻值。

在电路中，电感和电容是两种不同的元件，它们的特性和作用也不尽相同。

电感通常用于阻止交流电流的变化，而电容则用于存储电荷，并在交流电路中产生相位差。

而当它们并联在一起时，它们的作用就会相互影响，产生一些特殊的电路特性。

在并联电路中，电感和电容之间会产生一定的电流流动，而这个电流会对电路的总阻抗产生影响。

通过对电路进行分析，可以得到电感和电容并联的等效阻抗，从而更好地理解电路的特性和作用。

电感和电容并联的等效阻抗通常是一个复数，包括实部和虚部。

实部代表电路的电阻值，而虚部则代表电路的电感或电容值。

通过对等效阻抗的分析，可以确定电路的频率响应和相位特性，从而更好地控制和优化电路的性能。

总之，电感和电容并联的等效阻抗是电路中一个非常重要的概念，通过对其进行研究和分析，可以更好地理解电路的特性和作用，从而提高电路的性能和可靠性。

- 1 -。

并联电路基本特性总结并联电路是电子学中常见的电路配置之一，它由多个电阻、电容或电感等元件以并联的形式连接在一起。

本文将对并联电路的基本特性进行总结，并探讨其在电子电路中的应用。

一、并联电路的特点1. 电压相同：在并联电路中，各个元件的两端电压相等。

这是因为在并联连接的电路中，每个元件都直接连接到电源的正负极上，所以它们在电路中所受到的电压是相同的。

这一特点可以用来为不同元件提供相同的电压，以满足各自的工作需求。

2. 电流分流：在并联电路中，电流会分流通过每个并联元件。

具体而言，总电流将根据每个元件的电阻大小以不同比例分配到各个元件中。

并联电路的分流特性可以用来为不同元件提供适合的电流，以保证它们能正常工作。

3. 总电流等于分路的总和：在并联电路中，总电流等于各个分路电流之和。

这是由基尔霍夫定律所决定的，根据该定律可得出总电流等于电路中各个节点处电流的代数和。

这个特点可以用来计算并联电路中的总电流，从而更好地控制电路的工作状态。

二、并联电路的应用1. 分压电路：并联电路中的电阻元件可用于分压应用。

通过合理选择并联的电阻值，可以将输入电压分割为不同比例的输出电压。

分压电路在电子设备中广泛使用，用于电压调节、输入信号匹配等方面。

2. 分流电路：并联电路中的电阻元件可用于分流应用。

根据不同的电阻比例，可以将电流分配到不同的分支上，实现电流的分流效果。

这在需要为多个元件提供不同电流的电路中非常有用。

3. 广义电容器：并联电路中的电容元件可用于构造广义电容器。

将多个电容器以并联的方式连接在一起，可以实现更大的总电容值。

广义电容器在直流滤波、能量储存等场景中有着重要的应用。

4. 多声道音频系统：在多声道音频系统中，如多声道扬声器、耳机等，常会使用并联电路来连接多个声道。

这样可以保证每个声道都能获得相同的输入信号，并实现音频的同时播放。

三、并联电路的研究与发展随着电子技术的不断发展，对并联电路的研究也在不断深入。

电容与电感的串并联电路电容与电感是电路中常见的两种元件，它们在电路中具有重要的作用。

在电路中，电容和电感可以进行串联和并联的组合，形成串并联电路。

本文将探讨电容与电感的串并联电路的特点、计算方法和应用。

一、串联电路特点及计算方法串联电路是指电容和电感依次相连，电流在两个元件之间流动的电路。

串联电路中，电容和电感的总阻抗等于它们的阻抗之和。

电容和电感的串联电路示意图如下：（插入示意图）在串联电路中，电容的阻抗由以下公式计算：Zc = 1 / (jωC)其中，Zc为电容的阻抗，j为虚数单位，ω为频率，C为电容值。

电感的阻抗由以下公式计算：Zl = jωL其中，Zl为电感的阻抗，L为电感值。

串联电路的总阻抗Zs等于电容阻抗Zc和电感阻抗Zl之和：Zs = Zc + Zl串联电路中的电压分布按照电阻比例进行，即电压在电容和电感之间按阻抗比例分配。

二、并联电路特点及计算方法并联电路是指电容和电感同时连接在电路中，电流分别通过电容和电感的电路。

并联电路中，电容和电感的总阻抗等于它们的阻抗之和的倒数。

电容和电感的并联电路示意图如下：（插入示意图）在并联电路中，电容的阻抗由以下公式计算：Zc = 1 / (jωC)电感的阻抗由以下公式计算：Zl = jωL并联电路的总阻抗Zp等于电容阻抗Zc和电感阻抗Zl的倒数之和：Zp = 1 / (1/Zc + 1/Zl)并联电路中的电流分布通过电压比例进行，即电流在电容和电感之间按电压比例分配。

三、串并联电路的应用串并联电路在电子电路中有广泛的应用。

以下是几个典型的应用场景：1. 高通滤波器和低通滤波器：串并联电路可以用于构建不同频率特性的滤波器。

通过调节电容和电感的参数，可以实现对特定频率的信号进行滤波，达到去除高频或低频成分的目的。

2. 变压器：串并联电路在电力系统中常被用于构建变压器。

变压器通过串联和并联的电感，实现对电压的升降转换，并且能够有效进行能量传输。

3. 谐振电路：串并联电路可以用于构建谐振电路。

并联的电压并联的电压是指在电路中，多个电阻、电容或电感等元件以并联的方式连接时，各个元件的电压相同。

这是由于并联电路中，各个元件之间是平行连接的，电流会在各元件之间分流，而电压则保持一致。

并联电路是电路中常见的一种连接方式。

在并联电路中，各个元件之间的电流是相等的，而电压则保持一致。

这种特性使得并联电路在实际应用中具有广泛的用途。

我们来看一个简单的并联电路。

假设有两个电阻R1和R2以并联的方式连接在电路中。

当电路中有电流通过时，根据欧姆定律，电阻两端的电压可以表示为U=IR，其中U表示电压，I表示电流，R表示电阻。

在并联电路中，假设电阻R1两端的电压为U1，电阻R2两端的电压为U2。

由于并联电路中电压保持一致，所以有U1=U2。

当电路中有电流I通过时，根据欧姆定律，可以得到U1=IR1和U2=IR2。

由于U1=U2，所以有IR1=IR2。

这说明在并联电路中，各个电阻上的电流是相等的。

除了电阻，电容和电感也可以以并联的方式连接在电路中。

在并联电路中，电容和电感元件之间的电压也是相同的。

这是因为在并联电路中，电流会在各个元件之间分流，而电压则保持一致。

并联电路的特性使得它在实际应用中具有广泛的用途。

例如，在家庭电路中，我们常常可以看到多个电器设备以并联的方式连接在电路中。

这样做的好处是，每个电器设备都可以获得相同的电压供应，从而正常工作。

在电子电路中，多个电容或电感元件也可以以并联的方式连接在电路中。

这样做可以改变电路的频率响应，实现滤波功能。

并联的电压在工程领域中也有重要的应用。

例如，在电力系统中，多个变压器可以以并联的方式连接在电路中，共同为用户提供电能。

这样做可以增加供电能力，提高电力系统的可靠性。

并联的电压是指在电路中，多个元件以并联的方式连接时，各个元件之间的电压保持一致。

这种特性使得并联电路在实际应用中具有广泛的用途。

无论是家庭电路、电子电路还是电力系统，都离不开并联电路的应用。

通过合理设计和应用，并联电路可以为我们的生活和工作带来很多便利和好处。

考试试题低压电工计算机考试题库一、判断题；(一)电工基础1.并联电路中各支路原件上的电流必定相等。

B2.几个不等值电阻并联，每个电阻上的电压也不等。

B3.串联电路中各元件上的电压必定相等。

B4.导体在磁场中运动时，必定会产生感应电动势。

B5.法拉第电磁感应定律表明，线圈内感应电动势的大小与线圈中的磁通变化率成正比，且与线圈的圈数成正比。

A6.当电源的频率为0时感抗不为0 B7.在纯电感正旋交流电路中，电压与电流相位差为2分之派，在相位上的电流超前于电压。

B8.系统中当无功功率过补偿时，功率因数的数值将大于一。

B9.为了区别交流电相序，分别用黄绿红表示L1 L2 L3 A10.电动势和电压是同一概念，指电路中任意两点间的电位差。

B11.当电路属于开路，电路中电流为零，此时电源两边的空载电压在数值上等于电源的电动势。

U=E A12.容抗与频率的关系是频率越高，容抗越大。

B13.大小方向随时间变化的电流成为交流，工业用交流电是按照郑玄规律变化的，因此成为正旋交流电。

A14在纯电容正旋交流电路中，电压与电流相位差为2分之派，在相位上电流超前于电压。

A15.基尔霍夫第二定律说明，任何一个闭合回路中，在任意时刻电动势（电位升）的代数和等于各电阻上的电压（电位降）的代数和。

A16.左手定责是确定感应电动势的定则。

B17.在纯电阻正旋交流电路中，电流与电压的相位差为零。

A18.对于高频电流，感抗数值大，因此，线圈有抑制高次谐波通过的作用。

A19.电阻，电感，电容的并联电路中，当容抗与感抗相等时将发生电压谐振。

B20.对称三相电路功率也可以用三个单相电路的方法计算。

B21.用向量表达正玄交流电时，向量顺时针转是超前方向，逆时针转是滞后方向。

B22.基尔霍夫定律包括；节点电流定律（第一定律）和回路电压定律（第二定律）。

A23.相序是指三相交流电最大值出现的顺序。

A24.稳压二极管不能工作在反向击穿状态。

B25.晶体三极管既能用于交流点放大也能用于直流放大。

rlc电路串并联电路电流
在RLC电路中，电流的计算可根据串联电路和并联电路的特点来进行。

1. RLC电路的串联电路电流计算:
在RLC电路的串联电路中，电流沿着电流源和电阻、电感和电容依次流动，且电流大小相等。

因此，电流可以由电压和阻抗来计算。

假设电源电压为V，电阻为R，电感为L，电容为C，经过时间t后的电流为I，
则有以下公式：
V = IR + L(di/dt) + 1/C*q(t)
其中，di/dt表示电感的电流变化率，q(t)表示电容器的电量随时间的变化率。

2. RLC电路的并联电路电流计算:
在RLC电路的并联电路中，电流被分成两条路径，一条通过电阻，一条通过电感和电容。

根据欧姆定律和基尔霍夫电流定律，可以计算出总电流。

假设电源电压为V，电阻为R，电感为L，电容为C，经过时间t后的总电流为I，
则有以下公式：
V = IR = L(di/dt) + 1/C*q(t)
其中，di/dt表示电感的电流变化率，q(t)表示电容器的电量随时间的变化率。

需要注意的是，上述公式只适用于简单的RLC电路，对于复杂的RLC电路需要利用复杂的电路分析方法来计算电流。

电路中的串并联与等效电阻电路的串联、并联是电路中最基础的连接方式，通过串并联可以实现电路中电阻、电流和电压的灵活组合。

在电路中，串联是指将多个电阻、电容或电感连接在一条路径上，而并联则是将多个电阻、电容或电感连接在一个节点上。

本文将详细介绍电路中的串并联以及等效电阻的原理与计算方法。

一、串联电路的特点与计算方法串联电路是指将多个电阻依次连接在一起，电流在各个电阻之间依次流动。

串联电路中，电流相同，电压分配根据电阻值的大小进行。

计算串联电路的总电阻时，只需将各个电阻值相加即可。

例如，有三个电阻分别为R1、R2和R3，它们依次串联在一起。

则串联电路的总电阻Rt可由以下公式计算得出：Rt = R1 + R2 + R3当电路中的电阻数量较多时，可以通过计算器或电路模拟软件来快速计算总电阻。

二、并联电路的特点与计算方法并联电路是指多个电阻、电容或电感连接在一个节点上，电压在各个元件之间相同，电流分配根据元件的电阻值进行。

在计算并联电路的总电阻时，需要应用并联电阻的公式。

例如，有三个电阻分别为R1、R2和R3，并联在一个节点上。

则并联电路的总电阻Rt可由以下公式计算得出：1/Rt = 1/R1 + 1/R2 + 1/R3类似地，当并联电路中的元件数量较多时，可以借助计算器或电路模拟软件来快速计算总电阻。

三、串并联电路的等效电阻在电路中，多个电阻、电容或电感可以通过串联或并联的方式组合在一起，形成串并联电路。

对于串并联电路，可以通过等效电阻来简化分析与计算。

对于串联电路，它的等效电阻等于各个电阻值的总和，如前述所示。

对于并联电路，它的等效电阻可以应用并联电阻公式进行计算。

当电路中既存在串联又存在并联时，可以借助串并联电路的等效电阻进行分析。

可将各个串并联电路的等效电阻依次计算，最终得到整个电路的等效电阻。

四、电路中的等效电阻应用等效电阻在电路设计与分析中有着重要的应用。

通过等效电阻，可以将复杂的电路简化为一个电阻，从而简化计算与分析的复杂度。

课 题 8－6电阻、电感、电容的并联电路时间:12月20日 教学目标 1．掌握RLC 并联电路总电流和电压的相位关系、大小关系，会用相量图分析。

2．掌握RLC 并联电路的两个特例。

教学重点 会用相量图分析RLC 并联电路总电流和电压的相位关系、大小关系。

教学难点 1．画相量图。

2．总电流与电压的相位关系。

课前复习1．RLC 串联电路的相量图。

2．RLC 串联电路中，端电压和电流之间的关系。

第六节 电阻、电感、电容的并联电路一、RLC 并联电路：由电阻、电感和电容并联组成的电路 1．电路设在AB 两端加正弦交流电压u = U m sin ωt ，则各支路上的电流分别为：i R =I R m sin ωt I R =RU i L = I C m sin(ωt -2π) I L =LX U i C = I C m sin(ωt +2π) I C =CX U2．相量图以电压为参考相量 （1）X L > X C （2）X L < X C （3）X L = X C3．总电流和电压之间的关系 从分析相量图得出结论（1）总电流和电压的大小关系① 电流三角形：电路中总电流与各支路电流构成一个直角三角形，叫电流三角形。

I =22)(C L R I I I -+② 欧姆定律表达式I =ZU；|Z | = 22)11()1(1CL X X R -+→导纳三角形（2）相位间的关系① 当X L > X C 时，总电流超前端电压 ϕ 角，电路呈-------------性。

② 当X L < X C 时，总电流滞后端电压 ϕ 角，电路呈-------------性。

③ 当X L = X C 时，则I L = I C ，端电压与总电流同相，电路呈电阻性，电路的这种状态叫-------------谐振。

其中：总电流与端电压的相位差为：ϕ = ϕ i - ϕ u = - arctan RC L I I I -= - arctan RU X U X U C L ///-= - arctanGB B CL - < 0 感纳B L =L X 1；容纳B C =C X 1；电导G =R1，单位：西门子（S ）。