电阻电感电容串联电路.

电阻电感电容串联阻抗计算公式电阻、电感和电容是电路中常见的三种元件，它们分别有不同的特性和作用。

当它们串联连接在一起时，我们需要计算它们的总阻抗，以便更好地分析和设计电路。

本文将介绍电阻电感电容串联阻抗的计算公式，并解释其原理和应用。

电阻是电路中最基本的元件之一，它的单位是欧姆（Ω）。

电阻的作用是阻碍电流的流动，它消耗电能并产生热量。

在直流电路中，电阻的阻抗等于其电阻值。

但在交流电路中，电阻的阻抗取决于频率，可以用以下公式计算：电阻阻抗（Zr）= 电阻值（R）电感是一种具有自感性质的元件，它的单位是亨利（H）。

电感的作用是储存电能，并阻碍电流的变化。

当电流变化时，电感会产生电动势，使电流保持不变。

电感的阻抗与频率成正比，可以用以下公式计算：电感阻抗（Zl）= 2πfL其中，f是交流电路的频率，L是电感的感值。

电容是一种具有储能性质的元件，它的单位是法拉（F）。

电容的作用是储存电能，并阻抗电压的变化。

当电压变化时，电容会产生电荷，使电压保持不变。

电容的阻抗与频率成反比，可以用以下公式计算：电容阻抗（Zc）= 1 / (2πfC)其中，f是交流电路的频率，C是电容的容值。

当电阻、电感和电容串联连接在一起时，它们的总阻抗等于它们各自阻抗的矢量和。

可以用以下公式计算：总阻抗（Z）= √(Zr² + (Zl - Zc)²)其中，Zr是电阻的阻抗，Zl是电感的阻抗，Zc是电容的阻抗。

电阻电感电容串联阻抗的计算公式可以帮助我们分析和设计复杂的电路。

例如，在无线通信中，我们常常需要计算天线的输入阻抗，以便匹配收发器和天线之间的阻抗差异，从而提高信号传输效率。

通过了解电阻电感电容串联阻抗的计算公式，我们可以更好地理解和解决这类问题。

电阻电感电容串联阻抗的计算公式是电路分析和设计中的重要工具。

它们可以帮助我们计算电路中各个元件的总阻抗，从而更好地理解和解决实际问题。

通过学习和应用这些公式，我们可以提高电路设计的准确性和效率，为各种应用提供更好的解决方案。

串联RLC电路分析RLC电路是由电阻（R）、电感（L）和电容（C）组成的电路，它是电子电路中一种重要的电路形式。

在串联RLC电路中，电阻、电感和电容元件按顺序连接，电流依次通过它们。

在这篇文章中，我们将深入探讨串联RLC电路的分析。

首先，让我们来了解一些基本的概念。

电阻是电流通过时产生的电压降；电感是由螺线管制成的元件，当电流通过时，会产生一个磁场，这个磁场又会产生电压；电容是由两个电极和介质组成的元件，存储电荷，在电荷变化时产生电压。

在串联RLC电路中，电阻、电感和电容依次连接。

电路的总阻抗Z等于电阻、电感和电容阻抗的总和。

电流I通过电路，同时也通过电阻、电感和电容。

电压V则分别在电阻、电感和电容上产生。

我们可以通过基尔霍夫电压定律来分析串联RLC电路。

基尔霍夫电压定律指出，电路中环路内的电压之和等于零。

可以通过这个定律来得到电路中每个元件上的电压。

首先我们分析电感上的电压。

根据基尔霍夫电压定律，电感上的电压等于电感的自感电压减去电感上的电压降。

自感电压可以表示为L(di/dt)，其中L是电感的电感系数，i是通过电感的电流，dt是时间的微分。

电感上的电压降由欧姆定律计算，即IR，其中I是通过电感的电流，R是电感的内阻。

接下来我们分析电容上的电压。

电容上的电压与电流通过它的速率成正比。

可以表示为1/C * ∫i dt，其中C是电容的电容系数。

最后我们分析电阻上的电压。

电阻上的电压由欧姆定律给出，即IR，其中I是通过电阻的电流，R是电阻的电阻系数。

在串联RLC电路中，电流I是恒定的，所以可以将电感、电容和电阻上的电压相加，得到电路的总电压。

这个总电压和电路中的总电流有关，可以表示为ZI，其中Z是串联RLC电路的总阻抗。

总阻抗可以用下式计算：Z=√(R^2+(ωL-1/ωC)^2)，其中R是电阻的电阻系数，L是电感的电感系数，C是电容的电容系数，ω是角频率（ω=2πf，f是电路的频率）。

根据总电压和总电流的关系，我们可以得到串联RLC电路的传输函数。

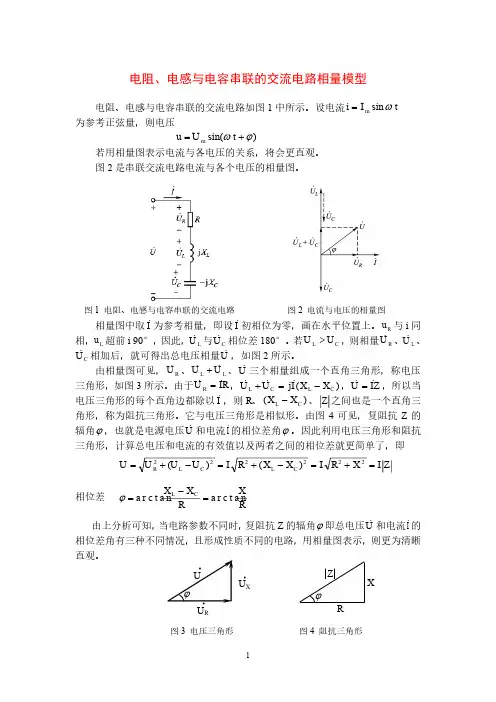
1 电阻、电感与电容串联的交流电路相量模型电阻、电感与电容串联的交流电路如图1中所示。

设电流t I i m ωsin = 为参考正弦量，则电压)sin(ϕω+=t U u m若用相量图表示电流与各电压的关系，将会更直观。

图2是串联交流电路电流与各个电压的相量图。

图1 电阻、电感与电容串联的交流电路 图2 电流与电压的相量图相量图中取I为参考相量，即设I 初相位为零，画在水平位置上。

R u 与i 同相，L u 超前i 90°，因此，L U 与CU 相位差180°。

若C L U U >，则相量R U 、L U 、CU 相加后，就可得出总电压相量U ，如图2所示。

由相量图可见，R U 、LL U U +、U 三个相量组成一个直角三角形，称电压三角形，如图3所示。

由于R I U R =，)(CL C L X X I j U U -=+ ，Z I U =，所以当电压三角形的每个直角边都除以I ，则R 、)(CL X X -、Z 之间也是一个直角三角形，称为阻抗三角形。

它与电压三角形是相似形。

由图4可见，复阻抗Z 的辐角ϕ，也就是电源电压U和电流I 的相位差角ϕ。

因此利用电压三角形和阻抗三角形，计算总电压和电流的有效值以及两者之间的相位差就更简单了，即Z I X R I X X R I U U U U C L C L R =+=-+=-+=222222)()(相位差 RX R X X C L a r c t a n a r c t a n =-=ϕ 由上分析可知，当电路参数不同时，复阻抗Z 的辐角ϕ即总电压U和电流I 的相位差角有三种不同情况，且形成性质不同的电路，用相量图表示，则更为清晰直观。

图3 电压三角形 图4 阻抗三角形 R X Zϕ U R U X ∙。

电容串联电感电阻,放电电流计算一、电容串联电感电阻的概念和特点1. 电容、电感和电阻的定义电容是指导体之间的电荷储存能力，以法拉（F）为单位。

电感是导体中感应感应电动势的能力，以亨利（H）为单位。

电阻是导体对电流的阻碍能力，以欧姆（Ω）为单位。

2. 电容串联电感电阻的概念电容串联电感电阻是指在电路中同时存在电容、电感和电阻的情况。

电容串联电感电阻会影响电路的频率响应和相位特性。

3. 电容串联电感电阻的特点- 电容串联电感电阻会使电路产生共振现象。

- 电路中的电容和电感会相互影响，导致电路的频率特性产生变化。

- 电路中的电容和电感会对电路的相位特性产生影响。

二、电容串联电感电阻的放电电流计算方法1. 电路分析方法- 根据电路中的电容、电感和电阻的数值，可以使用基尔霍夫电压和电流定律进行电路分析。

- 常用的电路分析方法有节点分析法和戴维宁定理。

- 电路分析可以得到电路中的电压、电流和功率等参数，从而计算放电电流。

2. 放电电流计算步骤- 根据电路图和参数表，确定电路中的电容、电感和电阻的数值。

- 使用基尔霍夫电压和电流定律，进行电路分析，得到电路中的电压和电流的表达式。

- 根据电路中的电压和电流的表达式，可以得到放电电流的计算表达式。

- 根据放电电流的计算表达式和电路中的参数，即可求得放电电流的数值。

3. 电容串联电感电阻的放电电流计算实例假设有一个电容串联电感电阻电路，电容为100μF，电感为10mH，电阻为100Ω。

现在需要计算在该电路中放电时的电流。

解：- 根据电路中的电容、电感和电阻的数值，可以得到电路的参数C=100μF，L=10mH，R=100Ω。

- 利用基尔霍夫电压和电流定律，进行电路分析得到电路中的电压和电流表达式。

- 根据电路中的电压和电流的表达式，可以得到放电电流的计算表达式。

- 代入电路的参数得到放电电流的数值。

四、总结- 电容串联电感电阻是电路中常见的元件组合，它会对电路的频率响应和相位特性产生影响。

RLC 串联交流电路》教案、教学目的1、理解并掌握RLC串联交流电路中电压与电流的数值、相位关系2、理解电压三角形和阻抗三角形的组成3、熟练运用相量图计算RLC串联电路中的电流和电压、教学重点1、掌握RLC串联电路的相量图2、理解并掌握RLC串联电路端电压与电流的大小关系三、教学难点1、RLC串联电路电压与电流的大小和相位关系四、教学课时五、教学过程一）复习旧课，引入新课：1 、复习单一参数交流电路i i2、引出问题 正弦交流电路一定是单一参数特性吗 分析: 1、实际电路往往由多种元件构成，不同元件性质不同。

例如，荧光灯电路 2、交流电路中的实际元件往往有多重性质，如电感线圈存在一定的电阻, 匝与匝之间还有电容效应因此，单一参数交流电路知识一种理想情况，具有多元件、多参数的 电路模型更接近于实际应用的电路。

3、新的学习任务 研究多元件、多参数的交流电路（二）新课讲授沌电客宏涼电路 U U = /R U —jXJB图1 RLC串联交流电路1、电压与电流的关系i =T. sin fttf以电流作为参考，设表达式为U R三f稱Rsinet Uf=I^X,sm(eut + 90') 叱血(曲由基尔霍夫第二定律可知，U U R U L U Cu l m Rsin t I m X L sin( t 90 ) I m X C sin( t 90 )同频率正弦量的和仍为同频率的正弦量，因此电路总电压U也是频率为的正弦量。

正弦量可以用矢量表示，则⑴式为:U U R U L U C由单一元件交流电路中电压申.流的矢S关系;=iR- jXJ =［尺 +丿(X) =二RZjXJ負阻抗Z这是RLC串联电路中总电压和总电流的关系，形式和欧姆定律类似，所以也称相量形式的欧姆定律。

RLC串联电路中总电压和总电流的数值关系:U J u R (U L U C)2U R j(X L X c) I (R jX)l IZI J R2(X L X C)2I|Z|RLC串联电路中电压电流的相位关系ar如VC ar如需上述分析过程，我们用矢量表示正弦量，根据复数运算的相关知识进行分析得出了结尝试图2 RLC串联电路的相量图画船7cU J U R (U L U C )2I J R 2 (X L X C )2电压三角形各条边同除以电流有效值I ,可得到一个阻抗三角形:所示 RLC 串联电路中，已知u 220J2sin(314t 60 )V ,30 , L 127mH ,C 40 F 。

rlc串联电路计算
RLC串联电路的计算主要包括电阻、电感、电容之间的关系计算，以及阻抗、相位角、功率等的计算。

在RLC串联电路中，电流I与电阻R、电感L和电容C之间的关系可以用以下公式表示：I = (V / R) * sqrt(1 + (wL / R) ^ 2 - (wC / R) ^ 2)
其中，V是电压，R是电阻，L是电感，C是电容，w是角频率。

阻抗Z的公式为：
Z = R + j(wL - 1 / (wC))
其中，j是虚数单位。

相位角θ的公式为：
θ = atan((wL - 1 / (wC)) / R)
功率P的计算公式为：
P = V * I * cos(θ)
其中，cos(θ)是功率因数。

这些公式可以帮助我们计算RLC串联电路中的电流、阻抗、相位角和功率等参数。

需要注意的是，这些公式仅适用于线性时不变的RLC串联电路，且电容和电感值必须为实数。

教学设计方案学科名称：电工电子技术与技能授课班级：设计者：年月日第周教学过程结构教学环节教师活动学生活动教学媒体设计意图【一、复习】1．电阻和电感串联电路电流与电压关系。

2．电阻和电感串联电路电压三角形、阻抗三角形、功率三角形。

【二、引入新课】如果在电阻和电感串联电路的基础上再增加一个电容元件，电路所表现出的各种特征会有很大的差异，一些物理现象的原因和解释都更加复杂，例如谐振现象。

【三、讲授新课】4.4.1电流与电压的关系1．电路如图4.18所示，设电路中电流初相角为零，即i = I m sinω t那么u R = U R m sinωt =R I m sinω tu L = U L m sin (ω t +2π) = X L I m sin (ω t +2π)u C = U C m sin (ω t -2π) = X C I m sin (ω t -2π)u = u R + u L + u C=U R m sin ω t + U L m sin (ω t +2π) + U C m sin (ω t -2π)u = U m sin (ω t + ϕ )图4.18R、L、C串联电路2．矢量图，如图4.19所示（设X L > X C，即U L > U C）。

学生自己动手尝试画出矢量图，并分析其中的关系多媒体让学生认识RLC串联电路的特性掌握矢量图的画法图4.19R、L、C串联电路矢量图由矢量图可见：（1）电源电压矢量为电阻、电感和电容电压矢量之和U = U R + U L + U C由矢量图可得U =22）（CLRUUU-+ϕ = arctanRCLUUU-可得电压三角形，如图4.20（a）所示。

(a)电压三角形 (b)阻抗三角形 (c)功率三角形图4.20R、L、C串联电路三角形（2）阻抗U =22）（CLRUUU-+= I22）（CLXXR-+U =22XR+I =|Z | I阻抗Z、电阻R和电抗X构成一个与图4.20（a）相似的三角形，如图4.20（b）所示，这个三角形不是矢量。