当前位置：文档之家 › 2.3连续型随机变量与随机变量的分布函数

2.3连续型随机变量与随机变量的分布函数

  • 格式：pps
  • 大小：1.98 MB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

2.3连续型随机变量

2.3连续型随机变量

f (x)
1
e ,
(
x) 2 2
2
2
其中 , ( >0)为常数
x
称X服从参数为 ,的正态分布或
高斯分布,记为 X～N( , 2)
1 f(x)
(1)关于直线x 对称;
2
(2)最大值为 1 ;
2
(3)在x 处有拐点.
o
x
可求得X的分布函数为:
F(x) 1 x
e
(
t )2 2 2
1 P( A1 A2 A3 )
1 P( A1 A2 A3 )
1 P( A1 )P( A2 )P( A3 )
=1[1P(A1)][1P(A2)][1P(A3)] =1e1
3. 正态分布
正态分布是实践中应用最为广泛,在 理论上研究最多的分布之一,故它在概率 统计中占有特别重要的地位
X的概率密度为:
f(x)的性质:
(1) f(x)≥0, <x<+
(2) f ( x)dx 1
(3) P(x1<X≤x2)=F(x2) F(x1)
x2 f ( x)dx
x1
( x1 x2 )
f(x)
P(x1<X≤x2)
x1
o x2 x
这条性质是密度函数的几何意义
注: 对连续型随机变量X和任意实数a, 总有P(X=a)=0 即, 取单点值的
若X～U[a, b], [c, c+l][a, b], 有:
P(c≤X≤c +l )
cl
c f ( x)dx
cl c
b
1
adx
b
l
a
这说明:
X落在[a,b]的子区间内的概率与子 区间的长度成正比,而与子区间的位置 无关

2.随机变量的分布函数、连续型

2.随机变量的分布函数、连续型

4 2 4 0, x 0,
故X的分布函数为
1 , 0 x 1,
F(x)
4 3 ,
1 x 2,
4
F(x)
1, 2 x.
1
O
0O
1
O
它是一条阶梯形曲线，
2
x
设离散型随机变量X 的分布律为
P( X xi ) pi , i 1,2, ,
则离散型随机变量X的分布函数
F( x) P( X x) P( X xi )
a, 2
得a 2
于是X的密度函数为 2e2 x ,
f (x) 0,
x0 x0
P( X 1) 2e2xdx e2 . 1
3、正态分布 如果连续型随机变量X的密度函数为
f (x)
1
( x )2
e
2 2
,xR
2
那么称随机变量X服从参数为， 2的正态分布，
～ 记为X N（， 2）, R, 0.
本节我们来研究一维随机变量取值的统计规律性。 为此先考虑下面的例子。
例1 设随机变量X在区间[0，1]上取值，当0 a 1
时，概率P（0 X a）与a2成正比例。
试求X的分布函数F（x）
解：X的分布函数为：
y
0
F
(
x)
x2
1
x0 0 x1
1 x
1 o1x
由此例我们看到，F ( x)处处连续，并且其
2
2
x, (3)
x 1 1 x F (xx).1
1
（3） 当x 1时, F( x)
x
f (t)dt
x
0dt 0
当 1 x 1时, F( x)
x f (t )dt

§2.3连续型随机变量及其概率密度

§2.3连续型随机变量及其概率密度

随机变量 X 的概率密度可以取为
f (x) F(x) 10,
a2 x2 , a x a, 其它.
上页 下页 返回
例3 某电子元件的寿命（单位：小时）是以
f x 1000
x2
x 100 x 100
为密度函数的连续型随机变量．求 5 个同类型的元件
在使用的前 150 小时内恰有 2 个需要更换的概率.
解：设A={ 某元件在使用的前 150 小时内需要更换}
则
PA
PX
150
150
f (x)d x
150
100
100 x2
d
x
检验 5 个元件的使用寿命可以看作
100150 x 100
1 3
是在做一个5重Bernoulli试验．
设B={ 5 个元件中恰有 2 个的使用寿命不超过150小时 }
则
P
B
连续型随机变量 X 可由其密度函数唯一确定． 还可以得出连续型随机变量 X 的分布函数一定连续．
2. 性质 由定义知道，概率密度 f (x) 具有以下性质：
f (x)
10 f ( x) 0.
20
f
( x)dx
1.
1
x
0 上页 下页 返回
10 f ( x) 0.
另外，可以证明:
20
f
( x)dx
(3)由
c
3 8
知
X
的概率密度为
f x
3 8
4 x
2
x2
0 x2
由 F ( x)
x
f
(x)d
x
得
0
其它
0,
x 0 0,
x0

§2.3 连续型随机变量及其分布

§2.3 连续型随机变量及其分布

（2）指数分布 若随机变量 的密度函数p( x) 为：
e x , x 0 p ( x) ( 0) ，则称 服从参数为 的指 0, x 0
数分布，记作 ~ E( )
指数分布是一种应用广泛的连续型分布，它 常被用来描述各种“寿命”的分布，例如无线电 电元件的寿命、电话问题中的通话时间等都可以
k ) 2 (k ) 1
注意 这个概率与 无关.
例2.3.7 设随机变量 （1）P(102 117) （2）常数a，使得

服从正态分布 N (108,9) 求
P( a) 0.95
解（1） P(102 117 ) (117 108 ) (102 108 )
2） F ( x) p(t )dt
xபைடு நூலகம்
x
注意
1) 求密度函数中的待定常数往往借助 2) 由密度函数求分布函数需要对自变
于密度函数的性质.
量的情形进行讨论.
例2.3.3 设连续型随机变量的分布函数为
0, x a xa F ( x) ,a x b b a 1, x b
则称 服从区间a, b 上的均匀分布，记作 ~ U a, b 向区间
a, b 上均匀投掷随机点，则随机点的
坐标 服从 a, b 上的均匀分布.在实际问题中， 还有很多均匀分布的例子，例如乘客在公共汽车 站的候车时间，近似计算中的舍入误差等都服从 均匀分布.
设随机变量 ~ U a, b ，则对任意满足c, d a, b
解：
P ( ) P ( 1
1) 2 (1) 1 0.6826
2) 2 (2) 1 0.9545

为随机变量X的分布函数

为随机变量X的分布函数

就会离去. 若该顾客一个月到银行5次, 以Y表示一个月内他未等
到服务而离开窗口的次数，写出Y的分布律，并求P{Y≥1}.
解：
X的分布函数
F
(
x)

1

1
e5
x
,
x 0;
0, x 0.
该顾客未得到服务事件为{X>10}，其概率为
p

P{X
10} 1 P{X
10} 1 F(10)
3
f (x)dx
3
f (x)dx
1
3 1dx 0 5 .


26
6
《概率统计》
返回
下页
结束
2.指数分布 若随机变量X的密度函数为
ex , x 0
f (x)
,
0,
x0
则称X服从参数为的指数分布, 记作X～E[] . >0为常数.
分布函数为
F
(
x)

2
即
A=1 .
《概率统计》
返回
下页
结束
四、常见连续型随机变量的分布
1.均匀分布
如果随机变量X的概率密度为
f
(x)

b
1
a
,
0,
a xb 其它
则称X在区间[a,b]上服从均匀分布, 记为X～U[a,b].
0,
xa
分布函数为
F
(x)


x b

a a
a xb
《概率统计》
返回
下页
结束
三、分布函数求法 例1.设随机变量X的密度函数为
f
(x)

概率统计2-3

概率统计2-3
0.08 0.06 0.04 0.02
f ( x )d x
a
b
F (b) F (a)
b x
a
Ch2-51
P( X a ) P( X a) 1 F ( a )
p ( x)
0.06 0.04 0.02
-5
5
a a
x
例1 设连续型 r.v 的 d.f 为
Ch2-52
1 其分布函数 F ( x) 2
作变量代换 s
t

x

(t )2 2 2

e
d t P( X x)
x F ( x)
P(a X b) F (b) F (a)
b a P( X a) 1 F (a)

(t ) e P(T t ) P( N (t ) 0) 0!
0
1 P(T t ), t 0
t
e
t
t0 t0 0, 0, f (t ) t F (t ) t e , t 0 1 e , t 0
即
T ~ E ( )
P( X ) F ( )
Ch2-72
1 F ( ) P( X )
1 2
0.3 0.25 0.2 0.15 0.1 0.05 -6 -5 -4 -3 -2 -1
Ch2-73
正态变量的条件
若 r.v. X
① 受众多相互独立的随机因素影响 ② 每一因素的影响都是微小的 ③ 且这些正、负影响可以叠加
1
x 0
对于任意的 0 < a < b, b x P(a X b) a e d x

23随机变量的分布函数与连续型随机变量


20
1
1 x
e 10 dx
e1
e2
10 10
2020年6月16日星期二
19
目录
上页
下页
返回
例： 设连续型随机变量的分布函数为
A Be2x，x 0
F(x)
1.求常数A,B；
0, x 0
2. 求X的概率密度函数 。
解：1.由分布函数的性质：F( ) 1
即 lim (A Be2x ) 1 x
一、均匀分布
定义：若连续型随机变量X的概率密度为
f
(x)
b
1
a
,
a x b,
0,
其它.
则称X服从 a,b 上的均匀分布。记为 X : U a,b
意义：X“等可能”地取区间 a,b中的值，这里的“等可能” 理解为： X落在区间 a,b中任意等长度的子区间内的可能性是
相同的。即等长度，等概率。
2e2x， x 0 f (x)
0, x 0
2020年6月16日星期二
21
目录
上页
下页
返回
指数分布的无记忆性：
对于一个非负的随机变量，如果对于一切s,t≥0，有
PX s t | X t PX s
则称这个随机变量具有无记忆性。
直观理解：若X表示仪器的寿命，那么上式说明:已 知此仪器已使用t时，它总共能工作s+t小时的概率等于 从开始使用时算起，它至少能工作s小时的概率．
1 3
2 3
[1
1 3
]
0.7486 (1 0.6293) 0.3779
2. PX 01 PX 01 (1) (1) 0.8413
3. P X 3 6 PX 9 PX 3

概率论-5分布函数、连续型

x →0
dF ( x ) (2) 若x是f(x)的连续点 则 的连续点, 是 的连续点 = f ( x) dx
因为: 因为
(4) P ( a ≤ X ≤ b ) = P ( a < X ≤ b ) = P (a ≤ X < b)
= P ( a < X < b ) = F (b) F (a ) = ∫ f ( x )dx
并不反映X取 值的概率.但这个值 ★密度函数值f(a)并不反映 取a值的概率 但这个值 越大,X取 附近值的概率就越大.也可以说 也可以说,在某点密 越大 取a附近值的概率就越大 也可以说 在某点密 度曲线的高度,反映了概率集中在该点附近的程度. 度曲线的高度,反映了概率集中在该点附近的程度. 1 证明 f ( x ) = 1 / 2e 证
a
b p{a < X ≤ b} = ?
请看下节! 请看下节!
总结
一,定义 二,举例
若离散型随机变量X的分布律为
P ( X = x k ) = p k , k = 1, 2 ,
则其分布函数为
F ( x ) = P{ X ≤ x } =
xi ≤ x
∑p
i
作业: 作业:P33
10,11,12. , ,
P( X = C ) = 1
则称这个分布为单点分布或退化分布, 则称这个分布为单点分布或退化分布,它的 分布函数为 0 x < c F ( x) = 1 x ≥ c
向平面上半径为1的圆 内任意投掷一个质点, 的圆D内任意投掷一个质点 例2 向平面上半径为 的圆 内任意投掷一个质点 表示该质点到圆心的距离. 以X表示该质点到圆心的距离 设这个质点落在 中 表示该质点到圆心的距离 设这个质点落在D中 任意小区域内的概率与这个小区域的面积成正比, 任意小区域内的概率与这个小区域的面积成正比 试求X的分布函数 的分布函数. 试求 的分布函数 解 当 x<0时, {X ≤ x} = φ 时 当0≤x≤1, 可得

连续型随机变量及其分布


P(X ) F() 1 F() P(X )
1 2
0.3 0.25
0.2 0.15
0.1 0.05
-6 -5 -4 -3 -2 -1
f (x) 的两个参数：
— 位置参数 即固定 , 对于不同的 , 对应的 f (x)
的形状不变化，只是位置不同．
— 形状参数
固定 ，对于不同的 ，f ( x) 的形状不同．
§2.3 连续型随机变量及其分布
连续型随机变量的概念
定义 设 X 是一随机变量，若存在一个非负 可积函数 f ( x ), 使得
x
F (x) f (t)dt x
其中F ( x )是它的分布函数， 则称 X 是连续型随机变量，f ( x )是它的概 率密度函数( p.d.f. )，简称为密度函数或概率 密度．
F
(
x)
1
0, ex
,
x0 x0
f ( x)
0
x
F( x) 1
0
x
对于任意的 0 < a < b,
P(a X b) b exd x a F (b) F (a) ea eb
应用场合 用指数分布描述的实例有：
随机服务系统中的服务时间；
电话问题中的通话时间；
无线电元件的寿命； 动物的寿命．
0.3 0.25
0.2 0.15
0.1 0.05
-6 -5 -4 -3 -2 -1
3
f (x) 的性质
图形关于直线x= 对称： f ( + x) = f ( - x)
在 x = 时, f (x) 取得最大值
1
2 在 x = ± 时, 曲线 y = f(x) 在对应的 点处有拐点．

连续型随机变量及其概率分布


14
Probability and Statistics
③正态分布（或高斯分布）
定义 设连续型随机变量X 的概率密度为
f (x)
1
e ,
(
x μ 2σ2
)2
x
,
2 πσ
其中 μ, σ(σ 0) 为常数,则称 X 服从参数为 μ, σ
的正态分布或高斯分布,记为 X ~ N ( μ,σ2 ).
15
②指数分布
Exponent(指数)
定义 设连续型随机变量 X 的概率密度为
f
(
x)
1 θ
e
x
θ
,
x 0,
0,
x 0.
其中 θ 0 为常数,则称 X 服从参数为 的指数
分布.记作X E( ).
10
Probability and Statistics
某些元件或设备的寿命服从指数分布.例如无线电元件的 寿命 、电力设备的寿命、动物的寿命等都服从指数分布.
故在计算X落在某一区间的概率时，可以不必 考虑区间是否包括端点,即
P{a X b} P{a X b} P{a X b} P{a X b}
4
Probability and Statistics
源“ 概 率 密 度 ” 名 称 的 来
设f (x)在点x处连续，则有
P(x X x x)
1
a
,
a
x
b,
1
0,
其他
ba
0a
则称X在区间（a,b)上服从均匀分布,
记为XU(a,b).
bx
7
Probability and Statistics
例2 等待时间 公共汽车每10分钟按时通过一车站， 一乘客在随机选择的时间到达车站.以X记他的等车 时间（以分计），则X是一个随机变量，且有
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.3 连续型随机变量与随机变量的分布函数一、分布函数二、概率密度函数三、常见连续型分布引例（1）求指针落在某个刻度如X=3的概率？（2）求指针落在区间（4，5]的概率？解：(1){3}()0A P X P A ====Ω的长度的长度54541(2){45}{5}{4}180181818P X P X P X -<≤==-==≤-≤-由上例，得到如下结论：1、X 在单点上的概率都为0，即0{}0P X x ==2{}{}{}P a X b P X b P X a <≤=≤-≤、 -(){}F x P X x =≤→分布函数{}P a X b <≤= () F b ()F a对于随机变量X ，既要知道X 的取值, 以及X 取这些值的概率; 而且更重要的是想知道X 在任意有限区间(a,b )内取值的概率.}{21x X x P ≤<}{}{12x X P x X P ≤-≤=21}{21x X x P ≤<分布函数).()(12x F x F -=?一、分布函数例如.],(21内的概率落在区间求随机变量x x X 1.概念的引入2.分布函数的定义说明(1) F (x )表示X 取值在－∞到x 的概率，可用来研究随机变量在某一区间内取值的概率情况..}{)(,,的分布函数称为函数是任意实数是一个随机变量设定义X x X P x F x X ≤=.)()2(的一个普通实函数是分布函数x x F例1随机变量X 的分布律为X 1234P0.20.10.40.3求X 的分布函数.,1时当<x 解}1{)(<≤=x X P x F 0=,21时当<≤x }{)(x X P x F ≤=}1{==X P 2.0=,32时当<≤x }{)(x X P x F ≤=}2{}1{=+==X P X P 3.0=,43时当<≤x }{)(x X P x F ≤=}3{}2{}1{=+=+==X P X P X P 7.0=,4时当≥x }{)(x X P x F ≤=1=X 1234P0.20.10.40.3{}{}{}{}{}{}⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤=+=+=<≤=+=<≤=<=.4,1,43,321,32,21,21,1,1,0)(x x X P X P X P x X P X P x X P x x F ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤<=.4,1,43,7.0,32,3.0,21,2.0,1,0x x x x x{}{}{}{}{}{}⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤=+=+=<≤=+=<≤=<=.4,1,43,321,32,21,21,1,1,0)(x x X P X P X P x X P X P x X P x x F即⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤<=.4,1,43,7.0,32,3.0,21,2.0,1,0x x x x x的分布函数为设随机变量XX解例2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤--<=.3,1,32,43,21,41,1,0)(x x x x x F .的分布律求X 321-P424141求（1）X 的分布函数；}.5.05.0{},11{≤≤-≤<-X P X P 练习题1、设随机变量X 的分布律为X -1012P1/152/153/159/15（2）⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤--<=.2,1,21,15/6,10,15/3,01,15/1,1,0)(x x x x x x F 15/5}11{=≤<-X P 答案152}5.05.0{=≤≤-X P);,(,1)(0)1(∞-∞∈≤≤x x F );(),()()2(2121x x x F x F <≤3.分布函数的性质xo1x 2x,0)(lim )()3(==-∞-∞→x F F x },{)(x X P x F ≤=0}{lim )(lim =≤=-∞→-∞→x X P x F x x xo xo ;1)(lim )(==∞∞→x F F x 证明,越来越小时当x ,}{的值也越来越小x X P ≤有时因而当,-∞→x .),(,,),(,}{,内必然落在时当而的值也不会减小增大时当同样∞-∞∞→-∞∈≤X x x X x X P x).(),()(lim )4(000∞<<-∞=+→x x F x F x x 即任一分布函数处处右连续.⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=.,1,,,0,,0,0)(221211x x x x x p x x p x x F .1}{lim )(lim =≤=∞→∞→x X P x F x x 所以xo )(x F ∙1x ∙2x ⋅1p ⋅2p ⋅1重要公式aXbP-≤<b=F((),}){)1(aFXP-=>Fa()2(a}1{).证明},X≤b<因为X≤=≤a}a{{}X{bX≤ba<Xa}≤,}{{∅=P≤XPb≤所以X=≤+<{}},a}{P{baXP-Xa=<b故≤()().}{abFF∑≤=≤=x x kk p x X P x F }{)(分布函数分布律}{k k x X P p ==离散型随机变量分布律与分布函数的关系二、连续型随机变量连续型随机变量X所有可能取值充满若干个区间。

对这种随机变量，不能象离散型随机变量那样, 指出其取各个值的概率，给出概率分布。

而是用“概率密度函数”表示随机变量的概率分布。

例1：某工厂生产一种零件，由于生产过程中各种随机因素的影响，零件长度不尽相同。

现测得该厂生产的100个零件长度(单位: mm)如下:2.3.1 频率直方图129, 132, 136, 145, 140, 145, 147, 142, 138, 144, 147, 142, 137, 144, 144,134, 149, 142, 137, 137, 155, 128, 143, 144, 148, 139, 143, 142, 135, 142,148, 137, 142, 144, 141, 149, 132, 134, 145, 132, 140, 142, 130, 145, 148, 143, 148, 135, 136, 152, 141, 146, 138, 131, 138, 136, 144, 142, 142, 137,141, 134, 142, 133, 153, 143, 145, 140, 137, 142, 150, 141, 139, 139, 150, 139, 137, 139, 140, 143, 149, 136, 142, 134, 146, 145, 130, 136, 140, 134,142, 142, 135, 131, 136, 139, 137, 144, 141, 136.这100个数据中，最小值是128，最大值是155。

128155作频率直方图的步骤(1).先确定作图区间[a, b] ;a= 最小数据-ε/ 2，b= 最大数据+ε/ 2，ε是数据的精度。

本例中ε= 1, a = 127.5, b = 155.5 。

(2). 确定数据分组数m= [1.87×(n−1)2/5+ 1]，组距d= (b − a) / m，= a+ i d, i= 0, 1, · · · , m；子区间端点ti(3).计算落入各子区间内观测值频数n i= #{x j∈[t i−1, t i)，j= 1, 2, · · · , n}，= n i / n，i= 1, 2, · · · , m；频率fi子区间频数频率(127.5, 131.5)60.06(131.5, 135.5)120.12(135.5, 139.5)240.24(139.5, 143.5)280.28(143.5, 147.5)180.18(147.5, 151.5)80.08(151.5, 155.5)40.04(4). 以小区间[ti-1，ti] 为底，y i=f i/ d( i=1, 2,…, m) 为高作一系列小矩形，组成了频率直方图，简称直方图。

由于概率可以由频率近似，因此这个直方图可近似地刻画零件长度的概率分布情况。

用上述直方图刻画随机变量X的概率分布情况是比较粗糙的。

为更加准确地刻画X的概率分布情况，应适当增加观测数据的个数,同时将数据分得更细一些。

当数据越来越多,分组越来越细时,直方图的上方外形轮廓就越来越接近于某一条曲线,这条曲线称为随机变量X的概率密度曲线，可用来准确地刻画X的概率分布情况。

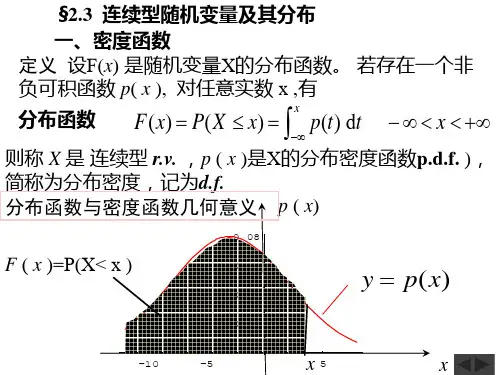
1. 概率密度函数定义1：若存在非负可积函数f (x ), 使随机变量X 取值于任一区间(a , b ] 的概率可表示成(1), )()( ⎰=≤<ba dx x fb X a P 则称X 为连续型随机变量，f (x )为X 的概率密度函数，简称概率密度或密度。

⎰∞-=x td t f )()()(x X P x F ≤=则称F(x )为X 分布函数。

这两条性质是判定函数f (x ) 是否为某随机变量X 的概率密度函数的充要条件。

密度函数的性质；0)( ).1(≥x f ；1 )( ).2(⎰∞∞-=dx x f f (x )与x 轴所围面积等于1。

例⎪⎩⎪⎨⎧≤>100,0,100,1002x x x⎪⎩⎪⎨⎧≤>0,0,0,10x x x ⎩⎨⎧≤≤-其他,0,20,1x ⎪⎩⎪⎨⎧≤≤其他,0,232121x ，下列函数中可作为某随机变量概率密度的是（）B ．C ．A ．D ．提示：概率密度的的非负性+ 归一性若x 是f (x )的连续点，则xx x X x P x ∆∆+≤<→∆)(lim 0=f (x )，(3). 对f (x )的进一步理解：故, X 的概率密度函数f (x )在x 这一点的值, 恰好是X 落在区间[x , x +△x ]上的概率与区间长度△x 之比的极限。

这里, 如果把概率理解为质量，f (x )相当于物理学中的线密度。

⎰∆+→∆∆=x x x x dt t f x )(1lim 0需要注意的是：概率密度函数f (x)在点a处取值，不是事件{X=a} 的概率。

但是，该值越大，X 在a点附近取值的概率越大。

若不计高阶无穷小，有：xX≈∆<≤+xP∆()x}.fx{x表示随机变量X取值于(x, x+△x]上的概率近似等于f (x ) ×△x。