讲连续型随机变量分布及随机变量的函数的分布(2020年10月整理).pdf
- 格式：pdf
- 大小：359.77 KB
- 文档页数：10
下载文档原格式
合集下载
连续型随机变量及其分布函数
0.9974
正态分布与标准正态分布之间具有下面的关系：
第34页，共40页。
引理
证明
若X ~ N ( μ,σ 2 ),则 Z X μ ~ N (0,1). σ
Z X μ的分布函数为 σ
P{Z
x}
P
X
σ
μ
x
P{
X
μ
σx}
1
(t μ)2
e μσx 2σ2 d t ,
2σ
令 t μ u,得 P{Z x} 1
p( x)
1
( x μ)2
e 2σ2 , x ,
2 πσ
其中 μ, σ(σ 0) 为常数,则称 X 服从参数为 μ, σ
的正态分布或高斯分布 , 记为 X ~ N ( μ, σ 2 ).
第24页，共40页。
正态分布概率密度函数的几何特征
(1)曲线关于 x μ 对称;
(2)当x μ时, p( x)取得最大值 1 ; 2 πσ
因而有Βιβλιοθήκη P{Y2} 3 2 21 2 3
2 3
3 2 31 3 3
2 0 3
20 . 27
第18页，共40页。
2. 指数分布
定义 设连续型随机变量 X 的概率密度为
ex , x 0,
p(x)
0,
x 0.
其中 0 为常数,则称 X 服从参数为 的指数
分布.
第19页，共40页。
0,
其它,
则称 X 在区间 (a, b)区间上服从均匀分布 ,
记为 X ~ U (a, b).
概率密度
函数图形
a
p( x)
o
b
第15页，共40页。
分布函数
正态分布与标准正态分布之间具有下面的关系：
第34页，共40页。
引理
证明
若X ~ N ( μ,σ 2 ),则 Z X μ ~ N (0,1). σ
Z X μ的分布函数为 σ
P{Z
x}
P
X
σ
μ
x
P{
X
μ
σx}
1
(t μ)2
e μσx 2σ2 d t ,
2σ
令 t μ u,得 P{Z x} 1
p( x)
1
( x μ)2
e 2σ2 , x ,
2 πσ
其中 μ, σ(σ 0) 为常数,则称 X 服从参数为 μ, σ
的正态分布或高斯分布 , 记为 X ~ N ( μ, σ 2 ).
第24页，共40页。
正态分布概率密度函数的几何特征
(1)曲线关于 x μ 对称;
(2)当x μ时, p( x)取得最大值 1 ; 2 πσ
因而有Βιβλιοθήκη P{Y2} 3 2 21 2 3
2 3
3 2 31 3 3
2 0 3
20 . 27
第18页，共40页。
2. 指数分布
定义 设连续型随机变量 X 的概率密度为
ex , x 0,
p(x)
0,
x 0.
其中 0 为常数,则称 X 服从参数为 的指数
分布.
第19页，共40页。
0,
其它,
则称 X 在区间 (a, b)区间上服从均匀分布 ,
记为 X ~ U (a, b).
概率密度
函数图形
a
p( x)
o
b
第15页，共40页。
分布函数
pdf第2.3节(连续型)几种常见的随机变量的分布
三个元件使用１０００小时后没有损坏的个数
Y B (3, e 1 ) 故 P (Y ≥ 1) = 1 P (Y = 0) = 1 (1 e 1 )3 ≈ 0.7474
注
①指数分布常用作各种“寿命”的近似分布. ②平均寿命为 λ
1
３、正态分布 定义 若
X ~ f ( x) =
1 2π σ
e
( xμ )2 2σ 2
Y=
X μ
σ
N (0,1)
例设
解
X~N(μ,σ2), P(X≤-1.6)=0.036, P(X≤5.9)=0.758, 求μ及σ.
1 .6 μ ) = 0.036 , 1 .6 μ < 0, 1.6 + μ
例 设 X ~ N（10，0.0004), Φ（2.5）=0.9938， 则 X 落 在区间（9.95，10.05）内的概率为( 0.9876).
x
若X~N(μ,σ2), 则 P(X<a)= Φ (
aμ )
例 设X~N(10,4),求P(10<X<13), P(|X-10|<2).
1310 1010
σ 解 P(10<X<13)= Φ( 2 ) Φ( 2 ) aμ ) =Φ(1.5)-Φ(0) P(X>a)= 1 Φ ( σ =0.4332 bμ aμ ) Φ( ) P(a<X<b)=Φ ( | X 10 | < 1) σ σ P(|X-10|<2)= P(
例 设随机变量X~U[2 ,5].现在对 X进行三次独立观 测,试求至少有两次观测值大于3的概率。
解 由题意得:
1 X ~ f ( x ) = 3 0 2≤ x ≤5 其它
２、指数分布 定义 若
Y B (3, e 1 ) 故 P (Y ≥ 1) = 1 P (Y = 0) = 1 (1 e 1 )3 ≈ 0.7474
注
①指数分布常用作各种“寿命”的近似分布. ②平均寿命为 λ
1
３、正态分布 定义 若
X ~ f ( x) =
1 2π σ
e
( xμ )2 2σ 2
Y=
X μ
σ
N (0,1)
例设
解
X~N(μ,σ2), P(X≤-1.6)=0.036, P(X≤5.9)=0.758, 求μ及σ.
1 .6 μ ) = 0.036 , 1 .6 μ < 0, 1.6 + μ
例 设 X ~ N（10，0.0004), Φ（2.5）=0.9938， 则 X 落 在区间（9.95，10.05）内的概率为( 0.9876).
x
若X~N(μ,σ2), 则 P(X<a)= Φ (
aμ )
例 设X~N(10,4),求P(10<X<13), P(|X-10|<2).
1310 1010
σ 解 P(10<X<13)= Φ( 2 ) Φ( 2 ) aμ ) =Φ(1.5)-Φ(0) P(X>a)= 1 Φ ( σ =0.4332 bμ aμ ) Φ( ) P(a<X<b)=Φ ( | X 10 | < 1) σ σ P(|X-10|<2)= P(
例 设随机变量X~U[2 ,5].现在对 X进行三次独立观 测,试求至少有两次观测值大于3的概率。
解 由题意得:
1 X ~ f ( x ) = 3 0 2≤ x ≤5 其它
２、指数分布 定义 若
2.4连续型随机变量及其分布
该图形越平坦，X的取值越分散。σ决定了图形中 峰的陡峭程度，称σ为形状参数。
正态分布由它的两个参数μ
和σ唯一确定，当μ和σ不同
时，正态分布也不同。
Ⅲ. 正态分布的分布函数
设 X ~ N (, 2 ) ，X 的分布函数是
F(x)
x
2 -
而 X ~ N(0, 1)，即 X 服从标准正态分布的分布函数为
FY ( y)
1
y u2
e 2 du ( y)
2
所以 Y X ~ N (0,1)
标准正态分布 的分布函数
结论
① 若X ~ N( , 2 ),Y X ~ N 0,1.
② 若 X ~ N(, 2 )，则它的分布函数可以写成
FX
(x)
P{X
x}
P{
X
x
}
(
x
)
例 P{ a X b } P{ a Y b }
的概率密度函数的充要条件。 x
③ 对于任意的数 a b 有
f (x)
P{a X b} P{a X b}
P{a X b} P{a X b} P{a X b}
1 0abx
b
a f (x)dx F (b) F (a)
连续型随机变量 X 落在某区间[a, b]上的概率为F(x)
这里事件 {X a} 并非不可能事件，但 P{X a} 0
可见，由P(A) 0，不一定能推出A为不可能事件； 由P(B) 1，不一定能推出B为必然事件。
称A 为几乎不可能事件，B 为几乎必然事件.
判断下列函数是否为某随机变量的概率密度
例1
f
(x)
(1
1
x2
)
(- x )
正态分布由它的两个参数μ
和σ唯一确定，当μ和σ不同
时，正态分布也不同。
Ⅲ. 正态分布的分布函数
设 X ~ N (, 2 ) ，X 的分布函数是
F(x)
x
2 -
而 X ~ N(0, 1)，即 X 服从标准正态分布的分布函数为
FY ( y)
1
y u2
e 2 du ( y)
2
所以 Y X ~ N (0,1)
标准正态分布 的分布函数
结论
① 若X ~ N( , 2 ),Y X ~ N 0,1.
② 若 X ~ N(, 2 )，则它的分布函数可以写成
FX
(x)
P{X
x}
P{
X
x
}
(
x
)
例 P{ a X b } P{ a Y b }
的概率密度函数的充要条件。 x
③ 对于任意的数 a b 有
f (x)
P{a X b} P{a X b}
P{a X b} P{a X b} P{a X b}
1 0abx
b
a f (x)dx F (b) F (a)
连续型随机变量 X 落在某区间[a, b]上的概率为F(x)
这里事件 {X a} 并非不可能事件，但 P{X a} 0
可见，由P(A) 0，不一定能推出A为不可能事件； 由P(B) 1，不一定能推出B为必然事件。
称A 为几乎不可能事件，B 为几乎必然事件.
判断下列函数是否为某随机变量的概率密度
例1
f
(x)
(1
1
x2
)
(- x )
2-2随机变量的分布函数与连续型随机变量
F(x) 是 (∞, +∞) 上的连续函数;
对于连续型随机变量X , P(X = a) = 0
事实上 X a a x X a , x 0
0 P X a P a x X a a f ( x )d x ax
a
0 P( X a ) lim
f ( x )d x 0 P X a 0
3. 连续型随机变量密度函数的性质
f (x) 0
f (x)dx F () 1
注1：常利用这两个性质检验一个函 数能否作为连续型随机变量的密度.
注2：由于改变密度函数在有限个点 的函数值不影响积分，故允许改变 它在有限个点的值为任意非负数。
在 f ( x ) 的连续点处，F( x ) f ( x )
P(a X b)
0.06 0.04 0.02
-10
a-5
b5
x
P(a X b)
b
F (b) F (a) a f ( x)dx
P(X b) P(X b) F(b) b f ( x)dx P(X a) P(X a) 1 F(a) a f ( x)dx
P X 1.5 F 1.5 F 1.5 0
0.7 lim F x 0.7 0.7 0 x1.5
练习 设随机变量 X 1 2 3
X的分布律。
P
1 2
a
1 6
求 1）a 及分布函数
2 )
P
5 4
X
5 2
,
P 2 X 4
解：1 ) 1 a 1 1 a 1 ,
26
P X 0 0 X 1 X 1 1 X 2 X 2 2 X x 0.1 0.6 0.3 1
0,
F
(
x
)＝00..71
连续型随机变量及其分布
下面我们介绍一种最重要的正态分布
标准正态分布
3)、标准正态分布
0 , 1 的正态分布称为标准正态分布.
其密度函数和分布函数常用 ( x)和 ( x) 表示：
1 ( x ) e , x 2 t2 ( x) 1 x 2 (x) e dt 2
P ( a X b ) P ( a X b )
(ii) 由P(X=a)=0 可推知
P ( X R a ) ( x ) d P x ( X a ) 1 f
而 {X=a} 并非不可能事件 并非必然事件 { X R { a }} 可见， 由P(A)=0, 不能推出 A
0 xa F ( x) b a 1 xa a xb xb
见书P52 图2-8
均匀分布常见于下列情形： 如在数值计算中，由于四舍五 入，小数 点后某一位小数引入的误差； 公交线路上两辆公共汽车前后通过某汽 车停车站的时间，即乘客的候车时间等.
例3 某公共汽车站从上午7时起，每15分钟来 一班车，即 7:00，7:15，7:30, 7:45 等时刻 有汽车到达此站，如果乘客到达此站时间 X 是 7:00 到 7:30 之间的均匀随机变量, 试求他候车 时间少于5 分钟的概率. 解：以7:00为起点0，以分为单位
t e t 0 f( t) F '( t) 0 0 t
1 P ( X 0 ) 1 e t
t
3.正态分布
正态分布是应用最 广泛的一种连续型分布. 德莫佛最早发现了二项概 率的一个近似公式，这一公式 被认为是正态分布的首次露面.
德莫佛
正态分布在十九世纪前叶由 高斯加以推广，所以通常称为高 斯分布.
2.3连续型随机变量及其分布
2、指数分布 定义3 设连续型随机变量X的概率密度为
ex, x0,
f (x)0,
其它 ,
其中λ >0为常数,则称随机变量X服从参数为θ 的 指数分布.
分布函数为
1ex, x0,
F(x) 0,
其它 .
概率论与数理统计
数学与计算科学学院 徐 鑫
可得：
（1）P(Xt)et(t0) （2）P ( t 1 X t2 ) e t 1 e t2 ( 0 t 1 t2 )
P ( 1 0 X 1 5 ) P ( 2 5 X 3 0 ) 1 5 1 d x 3 0 1 d x 1
1 0 3 0 2 5 3 0 3
概率论与数理统计
数学与计算科学学院 徐 鑫
练习 设K在(0,5)上服从均匀分布,求方程
4 x24 K x K 20
(1)P{X10}0 10P{X10}00 1F(10)00
0,
x 1b,
a a
,
x a, a x b, x b.
概率论与数理统计
数学与计算科学学院 徐 鑫
均匀分布的概率密度的图形
均匀分布的特点是:随机变量X落入(a,b)中任意等长 度的小区间内的概率都相等；此概率与子区间的长度 成正比，而与子区间的起点无关。
均匀分布的分布函数的图形
概率论与数理统计
数学与计算科学学院 徐 鑫
例3 设公交车站从上午7时起，每15分钟来一班车. 某乘客在7时到7时半之间随机到达该站，试求 他的候车时间不超过5分钟的概率.
解：该乘客于7时过X分到达该车站.依题意 X U(0,30) 候车时间不超过5分钟，即10X15或 25X30
第6讲 随机变量的分布函数,连续型随机变量
类似可求得
P (a < X < b ) = F (b − 0) − F (a ) P (a ≤ X < b ) = F (b ) − F (a − 0)
例5 设随机变量X的分布函数：
x < 0, , ⎧ 0 ⎪ F ( x ) = ⎨ x + 1 / 3 , 0 ≤ x < 1 / 2, ⎪ 1 x ≥ 1/ 2 , ⎩ 计算 P ( X = 0), P ( X = 1/ 4), P ( X ≥ 1/ 4), P (0 < X ≤ 1/ 3),
F ( x) = P( X ≤ x) ⇒ 0 ≤ F ( x) ≤ 1 当x沿数轴无限向左移动（即 x → +∞ ），则“随机点X 落在点x左边”这一事件趋于一个必然事件，从而其概率趋 于1,即 F ( +∞ ) = lim F ( x ) = 1 .
证
x →+∞
o
x
x
x
(2) 0 ≤ F( x) ≤ 1 且 lim F ( x) = 1, lim F ( x) = 0. x →+∞ x →−∞
F ( x ) = P ( X ≤ x ) = 0.
若0 ≤ x ≤ 2，则由题意
P (0 ≤ X ≤ x ) = kx 2 特别 x = 2 时, P (0 ≤ X ≤ x ) = 2 2 k = 1
x2 F ( x ) = P ( X ≤ x ) = P ( X < 0) + P (0 ≤ X ≤ x ) = 4
为 X 的分布函数. 2. 分布函数的性质 (1) F ( x ) 单调不减，即 ∀ x1 < x2 , F ( x1 ) ≤ F ( x2 ). (2) 0 ≤ F( x) ≤ 1 且 lim F ( x) = 1, lim F ( x) = 0.
P (a < X < b ) = F (b − 0) − F (a ) P (a ≤ X < b ) = F (b ) − F (a − 0)
例5 设随机变量X的分布函数：
x < 0, , ⎧ 0 ⎪ F ( x ) = ⎨ x + 1 / 3 , 0 ≤ x < 1 / 2, ⎪ 1 x ≥ 1/ 2 , ⎩ 计算 P ( X = 0), P ( X = 1/ 4), P ( X ≥ 1/ 4), P (0 < X ≤ 1/ 3),
F ( x) = P( X ≤ x) ⇒ 0 ≤ F ( x) ≤ 1 当x沿数轴无限向左移动（即 x → +∞ ），则“随机点X 落在点x左边”这一事件趋于一个必然事件，从而其概率趋 于1,即 F ( +∞ ) = lim F ( x ) = 1 .
证
x →+∞
o
x
x
x
(2) 0 ≤ F( x) ≤ 1 且 lim F ( x) = 1, lim F ( x) = 0. x →+∞ x →−∞
F ( x ) = P ( X ≤ x ) = 0.
若0 ≤ x ≤ 2，则由题意
P (0 ≤ X ≤ x ) = kx 2 特别 x = 2 时, P (0 ≤ X ≤ x ) = 2 2 k = 1
x2 F ( x ) = P ( X ≤ x ) = P ( X < 0) + P (0 ≤ X ≤ x ) = 4
为 X 的分布函数. 2. 分布函数的性质 (1) F ( x ) 单调不减，即 ∀ x1 < x2 , F ( x1 ) ≤ F ( x2 ). (2) 0 ≤ F( x) ≤ 1 且 lim F ( x) = 1, lim F ( x) = 0.
概统2.3节连续型随机变量及其概率分布
密度函数
(x)
1
x2
e2
2
是偶函数，分布函数记为
x
(x) 1
x t2
e 2dt
2
其值有专门的表供查.
2021/3/11
x
Ch2-82
0.4 0.3 0.2 0.1
-3 -2 -1
123
(0) 0.5 (x) 1 (x)
P(| X | a) 2 (a) 1
2021/3/11
0.3094
Ch2-86
例6 已知X ~ N (2, 2 ) 且 P( 2 < X < 4 ) = 0.3,
Ch2-78
Show[fn1,fn3]
小
0.5 0.4
大 0.3 0.2 0.1
-6
几何意义 数据意义
2021/3/11
-5 -4 -3 -2 -1
大小与曲线陡峭程度成反比 大小与数据分散程度成正比
Ch2-79
正态变量的条件 若 r.v. X
① 受众多相互独立的随机因素影响
② 每一因素的影响都是微小的 ③ 且这些正、负影响可以叠加
h(x) 2ax b, h(x) 2a
当 a 0 h(x) 2a 0 h(x) 有最小值
hmin (x) c b2 / 4a
2021/3/11
当且仅当 c b2 / 4a 0 时
Ch2-59
h(x) ax2 bx c 0
另外由
f (x)dx
(ax2
bx
1
c) dx
2021/3/11
皮肌炎图片——皮肌炎的症状表现
皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的， 全身性疾病，而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下：
连续型随机变量及其概率分布
0,
t 0, t 0.
7
二、连续型随机变量的密度函数 随机变量X 在区间( x, x x)上的平均概率分布密度:
P( x X x x) x
随机变量X 在点 x 处的概率分布密度(或概率密度)为:
P( x X x x)
f ( x) lim
x0
x
连续型随机变量的分布函数F x 与概率密度f x 有如下关系：
复习
§2.1 随机变量及其分布函数
一、随机变量的概念
基本事件
二、随机变量的分布函数
F(x) PX x
X ()
(1) 0 F(x) 1 (2) F(x) 是单调不减的函数；
(3) F() 1 F() 0
(4) F(x) 是右连续的函数.
(5) Px1 X x2 F(x2 ) F(x1 )
P(10 X 30) P(40 X 60) 30 1 dx 60 1 dx 2 .
10 60
40 60 3
19
均匀分布在实际中经常用到，比如一个半径为r的汽 车轮胎，当司机刹车时，轮胎接触地面的点与地面摩 擦会有一定的磨损. 轮胎的圆周长为2r，则刹车时与 地面接触的点的位置X应服从[0, 2r]上的均匀分布， 即 X～Ｕ[0, 2r] ，即在 [0, 2r] 上任一等长的小区间 上发生磨损的可能性是相同的，这只要看一看报废轮 胎的整个圆周上磨损的程度几乎是相同的就可以明白 均匀分布的含义了.
对任意实数 x ，有
x
F(x) f (t)dt
则 X 称为连续型随机变量，称 f (x)为 X 的概率密度函数
或分布密度函数，简称为概率密度或密度函数.
利用上述定义，我们可以很容易地推出概率密度的性质
11
t 0, t 0.
7
二、连续型随机变量的密度函数 随机变量X 在区间( x, x x)上的平均概率分布密度:
P( x X x x) x
随机变量X 在点 x 处的概率分布密度(或概率密度)为:
P( x X x x)
f ( x) lim
x0
x
连续型随机变量的分布函数F x 与概率密度f x 有如下关系：
复习
§2.1 随机变量及其分布函数
一、随机变量的概念
基本事件
二、随机变量的分布函数
F(x) PX x
X ()
(1) 0 F(x) 1 (2) F(x) 是单调不减的函数；
(3) F() 1 F() 0
(4) F(x) 是右连续的函数.
(5) Px1 X x2 F(x2 ) F(x1 )
P(10 X 30) P(40 X 60) 30 1 dx 60 1 dx 2 .
10 60
40 60 3
19
均匀分布在实际中经常用到，比如一个半径为r的汽 车轮胎，当司机刹车时，轮胎接触地面的点与地面摩 擦会有一定的磨损. 轮胎的圆周长为2r，则刹车时与 地面接触的点的位置X应服从[0, 2r]上的均匀分布， 即 X～Ｕ[0, 2r] ，即在 [0, 2r] 上任一等长的小区间 上发生磨损的可能性是相同的，这只要看一看报废轮 胎的整个圆周上磨损的程度几乎是相同的就可以明白 均匀分布的含义了.
对任意实数 x ，有
x
F(x) f (t)dt
则 X 称为连续型随机变量，称 f (x)为 X 的概率密度函数
或分布密度函数，简称为概率密度或密度函数.
利用上述定义，我们可以很容易地推出概率密度的性质
11
随机变量的分布函数、连续型
02
偏度是描述数据分布不对称性的量，即三阶中心矩与三阶原点矩的比值。偏度 大于0表示分布右偏，偏度小于0表示分布左偏。
03
峰度是描述数据分布形态陡峭或扁平程度的量，即四阶中心矩与四阶原点矩的 比值。峰度大于3表示分布比正态分布更陡峭，峰度小于3表示分布比正态分布 更扁平。
PART 04
连续型随机变量的应用
用。
PART 03
连续型随机变量的性质
REPORTING
WENKU DESIGN
概率密度函数（PDF）
概率密度函数（PDF）描述了随机变量取值在 某个区间的概率，即密度函数值与该区间长度 之积等于该区间内事件发生的概率。
PDF具有非负性，即对于所有实数x， PDF(x)≥0。
整个实数轴上的概率总和为1，即 ∫∞−∞f(x)dx=1，其中f(x)是随机变量的概率密 度函数。
在模拟连续型随机变量时，蒙特卡洛方法通过产生大 量随机样本，并计算其统计量，来估计随机变量的分
布函数和概率密度函数。
蒙特卡洛方法的优点是简单易行，适用于各种类型的 分布函数，但缺点是精度取决于样本数量，样本数量
越多，精度越高。
逆变换采样法
逆变换采样法是一种基于概率分布的反向抽样方法，即先从均匀分布的随机数中抽取样本，再通过概 率分布的反函数变换得到所需的随机变量。
THANKS
感谢观看
REPORTING
https://
正态分布的实际应用案例
金融领域
正态分布被广泛用于描述金融数据的分布，如股 票价格、收益率等。
自然现象
许多自然现象的分布呈现正态分布特征，如人类 的身高、智商等。
统计学
在统计学中，正态分布是最常用的分布之一，用 于描述数据的集中趋势和离散程度。
§3、连续型随机变量及其分布
综上所述，即得随机变量X的分布函数为
0, 当x 0时 1 F ( x) x 2 , 当0 x 2时 4 1, 当x 2时
对F(x)求导数，可得 x 2时 f ( x) F ( x) 2 0, 其它
P{a X b} F (b) F (a ) b a .
x
x
x 2 a x 2 a x dx a x arcsin C . 2 2 a
2 2
2
8
③当
x x 1 时，
1
F ( x)
f (t )dt
2 0 1 t 2 dt 0 1 1;
注：积分 所以
1
1
1 1 t dt 12 为单位圆面积一半． 2
19
正态分布密度函数 图形曲线的几何性质： (1)概率密度曲线 关于 x =μ为轴对称； (2)密度函数的 最大值为
f max ( x ) f ( )
(3)在点 x±μ处有拐点，凸凹区间为 (, ), ( , ), ( ,); (4)概率密度曲线以 x 轴为水平渐近线． 参数μ (X的数学期望)是其位置参数；参数σ (X的均方差)是其形状参数．
注：分布函数F(x)的不可导点仅两个，……
6
【例1】设随机变量X的概率密度为
求X的分布函数． 【解】 注意到其概率密度 f(x)是分段函数，因此 根据其分段定义区间(-∞,-1],(-1,1],(1,+∞)，分段 求其分布函数F(x)． ①当
x
2 1 x 2 , 1 x 1, f ( x) 其它, 0,
23随机变量的分布函数与连续型随机变量共34页
例：设某人到银行取款时的排队时间X (分钟)服从指
数分布，其概率密度为
f (x) e110x,
0,
x 0, x 0.
1.试确定常数λ;
2.计算排队时间超过10分钟的概率;
3.计算排队时间在10分钟到20分钟的概率．
14.09.2019
18
目录
上页
下页
返回
解：1.由
x 1
PX 1,
F
(x)
PX1PX2
1 x2 2x3
P X 1 P X 2 P X 3
3x4
P X 1 P X 2 P X 3 P X 4 4 x
P （ 1X2） ( 2 ) ( 1 ) 0 . 9 7 7 2 0 . 8 4 1 3 0 . 1 3 5 9
P （X1） ( 1 ) 1 ( 1 ) 1 0 . 8 4 1 3 0 . 1 5 8 7
相应的分布函数记为：
14.09.2019
x
(x)
1
t2
e 2dt
2π
25
目录
上页
下页
返回
(x)
(x)1(x)
(x)
(0) 1 2
x
o
x
若 X～N(0,1) 则 P （ a X b ） (b ) (a )
1 (x) x
例：若 X～N(0,1) P （ Xb） (b) P （ Xa ） 1 (a)
得
C 3
8
14.09.2019
10
目录
上页
下页
返回
第6讲(连续型随机变量与随机变量的分布函数)解析
P{X 1} P{X 1} 1 1 5；
326
当x 2 时，
F (x) P{X x} P{X 1} P{X 1} P{X 2} 1 1 1 1. 326
2 k(4x 2x2 ) d x 1，
0
所以
k(2x2 2 x3 ) 2
1
30
即 8k 1 3
所以 k 3 .
8
⑵ P {1 X 3}
3
f (x)d x
1
2 3 (4x 2x2 ) d x 30 d x
18
2
1 2
1
P {X 1} f (x) d x
0
0dx
1 3 (4x 2x2 ) d x 1
e , 2 2 x
2
其中μ和σ都是常数，σ>0，
则称X服从参数为、 2的正态分布，
记作 X ~ N(, 2) (Normal)
f (x)所确定的曲线叫作正态曲线.
f (x)
Ⅱ.性质
1
( x )2
e 2 2
2
1 f(x) 以 x =μ为对称轴；
2 f(x)在x=μ处取最大值 1 ；
f(x)与 x 轴所围 面积等于1.
0
(3) 连续型随机变量取任意指定值的概率为 0.
即：P{X a} 0, a为任意给定值. 由于P{X a} P{a x X a}
a
f (x) d x ax
则0 P{X a} lim a f (x) d x 0. x0 ax 故P{X a} 0.
例5 公共汽车车门的高度是按成年男性与车 门顶头碰头机会在0.01以下来设计的. 设某地 区成年男性身高 (单位: cm) X～N(170, 7.692), 问车门高度应如何确定?
326
当x 2 时，
F (x) P{X x} P{X 1} P{X 1} P{X 2} 1 1 1 1. 326
2 k(4x 2x2 ) d x 1，
0
所以
k(2x2 2 x3 ) 2
1
30
即 8k 1 3
所以 k 3 .
8
⑵ P {1 X 3}
3
f (x)d x
1
2 3 (4x 2x2 ) d x 30 d x
18
2
1 2
1
P {X 1} f (x) d x
0
0dx
1 3 (4x 2x2 ) d x 1
e , 2 2 x
2
其中μ和σ都是常数，σ>0，
则称X服从参数为、 2的正态分布，
记作 X ~ N(, 2) (Normal)
f (x)所确定的曲线叫作正态曲线.
f (x)
Ⅱ.性质
1
( x )2
e 2 2
2
1 f(x) 以 x =μ为对称轴；
2 f(x)在x=μ处取最大值 1 ；
f(x)与 x 轴所围 面积等于1.
0
(3) 连续型随机变量取任意指定值的概率为 0.
即：P{X a} 0, a为任意给定值. 由于P{X a} P{a x X a}
a
f (x) d x ax
则0 P{X a} lim a f (x) d x 0. x0 ax 故P{X a} 0.
例5 公共汽车车门的高度是按成年男性与车 门顶头碰头机会在0.01以下来设计的. 设某地 区成年男性身高 (单位: cm) X～N(170, 7.692), 问车门高度应如何确定?
第1次课 连续型随机变量和函数分布
满足连续型随机变量 设连续型随机变量X概率密度为 的两个最基本性质 ( x )2 1 2 2 f ( x) e , x 2
其中 , ( 0)为常数, 则称X服从参数为 , 的正态 分布, 记为X ~ N ( , 2 )。
显然f ( x) 0，下面来证明
例（等待时间）公共汽车每10分钟按时通过一车站，一乘客随 机到达车站.求他等车时间不超过3分钟的概率. 解 设X表示他等车时间（以分计），则X是一个随机变 量，且X的概率密度为 X ~ U[0,10).
1 , f ( x ) 10 0,
所求概率为 P{ X 3}
0 x 10, 其 它.
引理 若X ~ N ( , ) , 则 Z
2
X
~ N (0,1) .
证
Z
X
的分布函数为
X P{ Z x } P x P { X x }
1 2π
令 t
x
e
( t )2 2 2
＋
－
f ( x)dx 1
令
x
t, 得
1 e 2
( x )2 2 2
dx
1 2
e
t2 2
dt
利用广义积分
e
e
x2
dx , 有
于是
t2 2
dt 2
e
( x )2 2 2
1 2
P { X x } F ( x )
x 1 e 2πσ ( t μ )2 2σ 2
dt
其中 , ( 0)为常数, 则称X服从参数为 , 的正态 分布, 记为X ~ N ( , 2 )。
显然f ( x) 0，下面来证明
例（等待时间）公共汽车每10分钟按时通过一车站，一乘客随 机到达车站.求他等车时间不超过3分钟的概率. 解 设X表示他等车时间（以分计），则X是一个随机变 量，且X的概率密度为 X ~ U[0,10).
1 , f ( x ) 10 0,
所求概率为 P{ X 3}
0 x 10, 其 它.
引理 若X ~ N ( , ) , 则 Z
2
X
~ N (0,1) .
证
Z
X
的分布函数为
X P{ Z x } P x P { X x }
1 2π
令 t
x
e
( t )2 2 2
＋
－
f ( x)dx 1
令
x
t, 得
1 e 2
( x )2 2 2
dx
1 2
e
t2 2
dt
利用广义积分
e
e
x2
dx , 有
于是
t2 2
dt 2
e
( x )2 2 2
1 2
P { X x } F ( x )
x 1 e 2πσ ( t μ )2 2σ 2
dt
2.随机变量的分布函数、连续型
二、分布函数的性质
(1).0 ≤ F( x) ≤ 1, ∞ < x < ∞
(2).F( x1) ≤ F( x2), x1 < x2
(3). lim F( x) = 0,
x→∞
x → +∞
是单调非减的。 即F(x)是单调非减的。 是单调非减的 是右连续的。 即F(x)是右连续的。 是右连续的
lim F ( x ) = 1
F ( x ) = ∫ ∞ f ( t )dt , x ∈ R .
∞
x
为连续型随机变量， 那么称 X为连续型随机变量， 的概率密度函数。 称 f（ x）为 X的概率密度函数。 或概率密度或密度函数. 或概率密度或密度函数 由上面的定义可得下面两个结果: 由上面的定义可得下面两个结果 (1)在整个实轴上 在整个实轴上,F(x)是连续函数 是连续函数; 在整个实轴上 是连续函数 (2) 对f(x)的连续点 有 F ′( x ) = f ( x ) 的连续点,有 的连续点
F (b ) P {a < X ≤ b} = F (b ) F (a ). F (a )
分布函数
3.3
随机变量的分布函数
一、分布函数 定义 设 X 是一个 随机变量，称 随机变量， F( x) = P( X ≤ x) (∞ < x < +∞) 为 X 的分布函数. 或记作FX(x). 的分布函数 或记作
x
1 dt = 1 f ( t )dt = ∫1 2 π 1 t
1
3.5 常用的连续型随机变量 1、均匀分布 、
f (x)
1 ba
x b 设连续型随机变量X的密度函数为 设连续型随机变量 的密度函数为 a 1 , a≤ x≤b f ( x) = b a (a < b ) 其它 0, 上服从均匀分布， 则称随机变量 X在[a， b ]上服从均匀分布，记为 ： X ～ U [ a， b ] F ( x) 易知X的分布函数为
第三节连续性随机变量及其分布
设随机变量X的分布函数为:
1 x e 2 F ( x) 1 1 e x 2 x0 x0
求f(x)。
对 f(x)的进一步理解:
dF ( x ) f ( x) dx
若x是 f(x)的连续点，则：
F ( x x ) F ( x ) P{ x X x x } lim f(x) = lim x 0 x 0 x x
x
x
( x ) 1 ( x )
1. 若 X～N(0,1),
P{a X b} P{a X b} (b) (a ) X 2 2. 若X ~ N ( , ), 那么 Z ~N(0,1) x x F ( x ) P{ X x } P{ Z } ( )
x0 x 0,
1 13 x 2 (1) P{ X 2} e dx e 3 , 3 2
p{ X 3.5, X 1.5} (2) P{ X 3.5 | X 1.5} { X 1.5} 1 13 x e dx 3 3.5 1 13 x e dx 3 1.5
若X ～ U(a, b)，则对于满足a≤c<d ≤b 的c, d, 总有
P{c X d }＝ f ( x )dx＝
c
d
d
c
1 d c dx＝ ba ba
均匀分布常见于下列情形： 如在数值计算中，由于四舍五 入，小数点后某 一位小数引入的误差，例如对小数点后第一位进 行四舍五 入时，那么一般认为误差服从（-0.5, 0.5）上的均匀分布。
P{a X b} P{
a
b a ( ) ( )
Z
b
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
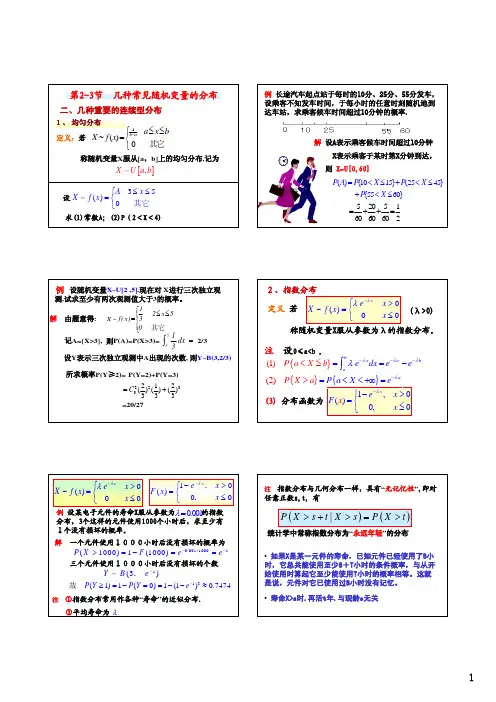
第七讲连续型随机变量（续）及 随机变量的函数的分布3. 三种重要的连续型随机变量 （1）均匀分布设连续型随机变量X 具有概率密度)5.4(,,0,,1)(⎪⎩⎪⎨⎧<<−=其它b x a ab x f则称X 在区间(a,b)上服从均匀分布, 记为X~U(a,b).X 的分布函数为)6.4(.,1,,,,0)(⎪⎪⎩⎪⎪⎨⎧≥<≤−−<=b x b x a a b a x a x x F（2）指数分布设连续型随机变量X 的概率密度为)7.4(,,0,0,e1)(/⎪⎩⎪⎨⎧>=−其它x x f x θθ其中θ>0为常数, 则称X 服从参数为θ的指数分布.容易得到X 的分布函数为)8.4(.,0,0,1)(/⎩⎨⎧>−=−其它x e x F x θ如X 服从指数分布, 则任给s,t>0, 有第二章 随机变量及其分布§4 连续型随机变量 及其概率密度Ox f (x )123123=1/3=1=2P{X>s+t | X > s}=P{X > t} (4.9) 事实上}.{e ee)(1)(1}{}{}{)}(){(}|{//)(t X P s F t s F s X P t s X P s X P s X t s X P s X t s X P t s t s >===−+−=>+>=>>⋂+>=>+>−−+−θθθ性质(4.9)称为无记忆性.指数分布在可靠性理论和排队论中有广泛的运用. （3）正态分布设连续型随机变量X 的概率密度为)10.4(,,e21)(222)(∞<<−∞=−−x x f x σμσπ其中μ,σ(σ>0)为常数, 则称X 服从参数为μ,σ的正态分布或高斯(Gauss)分布, 记为X~N(μ,2σ).显然f(x)≥0, 下面来证明1d )(=⎰+∞∞−x x f令t x =−σμ/)(, 得到dx edx et x 22)(2222121−∞+∞−−−∞+∞−⎰⎰=πσπσμ.1d 21d 21)11.4(π2d d e,,d d ,d e22)(20222/)(22/2222222======⎰⎰⎰⎰⎰⎰⎰∞∞−−∞∞−−−∞−+∞∞−+∞∞−+−∞∞−−x ex e r r I u t eI t I t x r u t t πσπθσμπ于是得转换为极坐标则有记f(x)具有的性质:f (x )的图形:Oxf (x )=5=50.2660.3990.798x Of (x )1.510.5（1）.曲线关于x=μ对称. 这表明对于任意h>0有P{μ-h<X ≤μ}=P{μ<X ≤μ+h}. （2）.当x=μ时取到最大值.π21)(σμ=fx 离μ越远, f(x)的值越小. 这表明对于同样长度的区间, 当区间离μ越远, X 落在这个区间上的概率越小。
在x=μσ±处曲线有拐点。
曲线以Ox 轴为渐近线。
X 的分布函数为)12.4(,d eπ21)(222)(⎰∞−−−=xt t x F σμσ特别:当μ=0, σ= 1时称X 服从标准正态分布. 其概率密度和分布函数分别用ϕ(x)和Φ(x)表示, 即有)14.4(.d e π21)()13.4(,21)(2/2/22⎰∞−−−=Φ=x t x t x e x πϕ易知 Φ(-x)=1-Φ(x) (4.15)人们已经编制了Φ(x)的函数表, 可供查用(见附表2).引理 若X~N(μ,2σ), 则)1,0(~N X Z σμ−=1F (x )0.5x O证明：的分布函数为σμ−=X Z得令,,d eπ21}{}{222)(u t t x X P x X P x Z P xt =−=+≤=⎭⎬⎫⎩⎨⎧≤−=≤⎰+∞−−−σμσσμσμσμσμ),(d eπ21}{2/2x u x Z P xu Φ==≤⎰∞−−由此知Z~N(0,1).若X~N(μ,2σ), 则它的分布函数F(x)可写成:)()16.4(}{}{)(σμσμσμ−Φ=−≤−=≤=x x X P x X P x F则对于任意区间(x1,x2], 有)17.4(.}{122121⎪⎭⎫ ⎝⎛−Φ−⎪⎭⎫ ⎝⎛−Φ=⎭⎬⎫⎩⎨⎧−≤−<−=≤<σμσμσμσμσμx x x X x P x X x P例如, 设X~N(1,4), 查表得.3094.06915.016179.0)]5.0(1[6179.0)5.0()3.0(210216.1}6.10{=+−=Φ−−=−Φ−Φ=⎪⎭⎫⎝⎛−Φ−⎪⎭⎫ ⎝⎛−Φ=≤<X P设X~N(μ,2σ), 由Φ(x)的函数表还能得到: P{σμ−<X<σμ+}=Φ(1)-Φ(-1)322368.26%95.44%99.74%=2Φ(1)-1=68.26% P{σμ2−<X<σμ2+}=Φ(2)-Φ(-2)=95.44%P{σμ3−<X<σμ3+}=Φ(3)-Φ(-3)=99.74%我们看到, 尽管正态变量的取值范围是(∞∞−,), 但它的值落在(σμ3−,σμ3+)内几乎是肯定的事. 这就是人们所谈的"3σ"法则.例１ 将一温度调节器放置在贮存着某种液体的容器内. 调节器整定在d °C, 液体的温度X(以°C 计)是一个随机变量, 且X~N(d, 0.52). (1) 若d=90, 求X 小于89的概率. (2) 若要求保持液体的温度至少为80的概率不低于0.99, 问d 至少为多少? 解 (1)所求概率为.0228.09772.01)2(1)2(5.090895.090}89{=−=Φ−=−Φ=⎭⎬⎫⎩⎨⎧−<−=<X P X P (2) 按题意需求d 满足.1635.81.327.25.080),327.2()327.2(199.015.0805.08015.0805.015.0805.0}80{99.0>−≤−−Φ=Φ−=−≤⎪⎭⎫⎝⎛−Φ⎪⎭⎫⎝⎛−Φ−=⎭⎬⎫⎩⎨⎧−<−−=⎭⎬⎫⎩⎨⎧−≥−=≥≤d dd d d d X P d d X P X P 故需亦即设X~N(0,1), 若z a 满足条件P{X>z a }=a, 0<a<1, (4.18)则称点z a 为标准正态分布的上a 分位点.由ϕ(x)的对称性知z 1-a =-z az常用的几个z a 值：1.2821.6451.9602.3272.5763.090z0.100.050.0250.010.0050.001（课间休息）随机变量的函数的分布例１ 设随机变量X 具有以下的分布律, 试求Y=(X-1)2的分布律.0.40.10.30.2p k2101X解 Y 所有可能值为0,1,4, 由P{Y=0}=P{(X-1)2=0}=P{X=1}=0.1, P{Y=1}=P{X=0}+P{X=2}=0.7, P{Y=4}=P{X=-1}=0.2,0.20.70.1p k410Y例２ 设随机变量X 具有概率密度⎪⎩⎪⎨⎧<<=.,0,40,8)(其它x x x f X求变量Y=2X+8的概率密度.解：分别记X,Y 的分布函数为F X (x),F Y (y). 下面先来求F Y (y)..2828}82{}{)(⎪⎭⎫⎝⎛−=⎭⎬⎫⎩⎨⎧−≤=≤+=≤=y F y X P y X P y Y P y F X Y§5 随机变量的函数的分布在实际中经常对某些随机变量的函数更感兴趣.例如, 在一些试验中, 所关心的随机变量往往不能由直接测量得到, 而它却是某个能直接测量的随机变量的函数. 比如我们能测量圆轴的直径d, 而关系的却是截面积A=pd2/4. 这里, 随机变量A 是随机变量d 的函数. 下面讨论如何由已知的随机变量X 的概率分布去求得它的函数Y=g(X)(g(•)是已知的连续函数)的概率分布.将F Y (y)关于y 求导数, 得Y=2X+8的概率密度为⎪⎩⎪⎨⎧<<−=⎪⎩⎪⎨⎧<−<⋅⎪⎭⎫ ⎝⎛−='⎪⎭⎫⎝⎛−⎪⎭⎫ ⎝⎛−=.,0,168,328,0,4280,2128812828)(其它其它y y y y y y f y f X Y 例３ 设随机变量X 具有概率密度f X (x),∞<<∞−x , 求Y=X 2的概率密度.解 分别记X,Y 的分布函数为F X (x), F Y (y). 由于Y=X 2≥0, 故当y ≤0时F Y (y)=0. 当y>0时有).()(}{}{}{)(2y F y F y X y P y X P y Y P y F X X Y −−=≤≤−=≤=≤= 将F Y (y)关于y 求导数, 即得Y 的概率密度为⎪⎩⎪⎨⎧≤>−+=.0,0,0)],()([21)(y y y f y f yy f X X Y例３结论的应用： 设X~N(0,1), 其概率密度为∞<<−∞=−x x x ,e π21)(2/2ϕ 则Y=X 2的概率密度为⎪⎩⎪⎨⎧≤>=−−.0,0,0,e π21)(2/2/1y y y y f y Y （5.1）(特注：y=0时概率为零，但并非不可能事件。
)此时称Y 服从自由度为1的2χ分布. 定理 设随机变量X 具有概率密度f X (x),∞<<∞−x , 又设函数g(x)处处可导且恒有g'(x)>0 (或恒有g'(x)<0), 则Y=g(X)是连续型随机变量, 其概率密度为）（其它2.5,0,)()]([)(⎩⎨⎧<<'=βαy y h y h f y f X Y 其中α=min(g(∞-),g(∞)),β=max(g(∞-),g(∞)), h(y)是g(x)的反函数.证 先设g'(x)>0. 此时g(x)在(∞-，∞)严格单调增加, 它的反函数h(y)存在, 且在(βα,)严格单调增加, 可导. 分别记X,Y 的分布函数为F X (x),F Y (y). 因Y 在(βα,)取值, 故 当α≤y 时, F Y (y)=P{Y ≤y}=0; 当y ≥β时, F Y (y)=P{Y ≥y}=1. 当βα<<y 时,F Y (y)=P{Y ≤y}=P{g(X)≤y}=P{X ≤h(y)}=F X [h(y)].将F Y (y)关于y 求导数, 即得Y 的概率密度)3.5(.,0,),()]([)(⎩⎨⎧<<'=其它βαy y h y h f y f X Y 对于g'(x)<0的情况同样可以证明, 有)4.5(.,0,)],()][([)(⎩⎨⎧<<'−=其它βαy y h y h f y f X Y合并(5.3),(5.4)式，命题得证。