23.2.1 中心对称
- 格式:ppt
- 大小:1.11 MB
- 文档页数:35

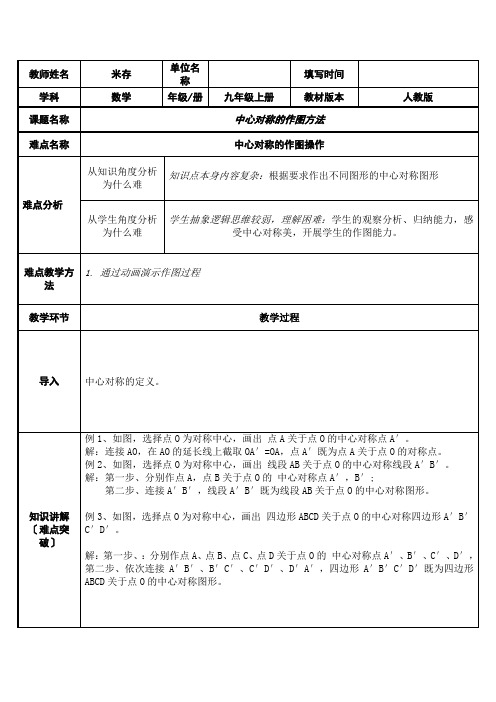




23.2.1中心对称学习目标:理解两个图形关于某一点中心对称的概念及性质,能作一个图形关于某一点的中心对称图形.学习重点:理解中心对称的概念和性质,能作中心对称图形.学习难点:性质的理解及作图.一.观察、思考与探究1.阅读课本P68,根据你的理解填空.把一个图形绕着某一个点旋转______,如果它能够与另一个图形______,那么称这两个图形关于这个点对称或中心对称,这个点叫做______,这两个图形中的对应点叫做关于中心的______.2.阅读课本P69,回答下列问题.如图,△ABC 和△A ’B ’C ’关于点O 中心对称,则 ⑴图中有几组“三点共线”?把它们写在下面.⑵图中有哪些等量关系?把它们写在下面.⑶请归纳“两图形关于某点中心对称”的性质.3.小试牛刀:如图,若四边形ABCD 与四边形CEFG 成中心对称,则它们的对称中心是______,点A 的对称点是______,E 的对称点是______.BD ∥______且BD =______.连结A ,F 的线段经过______,且被C 点______,△ABD ≌______.二.例题讲解1.作点A 关于点O 的2. 作△ABC 关于O 点的3. 作△ABC 关于A 点的 中心对称点A ’; 中心对称图形; 中心对称图形;4.右图两三角形关于某一点 中心对称,请设计两种方法, 找出对称中心,并说明理由.A OCDD三.练习与检测1.求作:四边形A ′B ′C ′D ′,使得四边形A ′B ′C ′D ′与四边形ABCD 关于O 点中心对称.2.如图,点O 为AC 边中点,⑴求作△ABC 关于O 点的中心对称图形; ⑵两个图形组成一个什么四边形?为什么?⑶若将该四边形绕点O 旋转180°,你有什么发现?3.不用刻度尺,在右面的方格图中 作出△ABC 关于O 点的中心对称图形.四.对比辨析 1.右图的△ABC 和△A ’B ’C ’ 分别满足什么关系?写在对应 图形的下面.2.根据你的认识,归纳两种对称的相同点和不同点.五.拓广与探索已知:直线l 的解析式为y =2x +3,若先作直线l 关于原点的对称直线l 1,再作直线l 1关于y 轴的对称直线l 2,最后将直线l 2沿y 轴向上平移4个单位长度得到直线l 3,试求l 3的解析式.。
人教版九年级数学上册23.2.2.1《中心对称》教案一. 教材分析人教版九年级数学上册第23章《中心对称》是学生在学习了平面几何相关知识的基础上,进一步引导学生探索中心对称的性质和运用。
本节内容通过具体的实例,让学生了解中心对称的定义,掌握中心对称图形的性质,并能够运用中心对称解决实际问题。
教材通过丰富的图片和实例,激发学生的学习兴趣,培养学生动手操作和观察分析的能力。
二. 学情分析九年级的学生已经具备了一定的几何知识基础,对平面几何图形有一定的了解。
但学生在学习过程中,可能对中心对称的概念和性质理解不够深入,需要通过大量的练习和操作来巩固。
此外,学生对实际问题的解决能力有待提高,需要通过具体的例子来引导和培养。
三. 教学目标1.了解中心对称的定义,掌握中心对称图形的性质。
2.能够运用中心对称解决实际问题,提高学生的应用能力。
3.培养学生的动手操作和观察分析能力,激发学生学习几何的兴趣。
四. 教学重难点1.中心对称的定义和性质。
2.中心对称在实际问题中的应用。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过具体的实例和问题,引导学生探索中心对称的性质,培养学生的动手操作和观察分析能力。
同时,学生进行小组合作学习,鼓励学生发表自己的观点和思考,提高学生的合作能力和沟通能力。
六. 教学准备1.准备相关的图片和实例,用于引导学生探索中心对称的性质。
2.准备一些实际问题,用于巩固学生对中心对称的应用。
3.准备黑板和粉笔,用于板书重要的概念和性质。
七. 教学过程1.导入(5分钟)通过展示一些图片,如天安门、蝴蝶等,引导学生观察这些图片的共同特点,引发学生对中心对称的思考。
让学生发表自己的观点,教师总结并引入中心对称的概念。
2.呈现(10分钟)教师通过展示一些实例,如将一张纸折叠后,对折线两侧的图形完全重合,引导学生探索中心对称的性质。
教师引导学生动手操作,观察分析中心对称图形的性质,如对称轴的性质、对称点的性质等。