下载文档原格式
第4章 静定结构的位移计算习题解答习题4.1 是非判断题(1) 变形体虚功原理仅适用于弹性体系，不适用于非弹性体系。
（ ） (2) 虚功原理中的力状态和位移状态都是虚设的。
（ ）(3) 功的互等定理仅适用于线弹性体系，不适用于非线弹性体系。
（ ） (4) 反力互等定理仅适用于超静定结构，不适用于静定结构。
（ ） (5) 对于静定结构，有变形就一定有内力。
（ ） (6) 对于静定结构，有位移就一定有变形。
（ ）(7) 习题4.1(7)图所示体系中各杆EA 相同，则两图中C 点的水平位移相等。
（ ） (8) M P 图，M 图如习题4.1(8)图所示，EI =常数。
下列图乘结果是正确的：4)832(12ll ql EI ⨯⨯⨯ （ ）(9) M P 图、M 图如习题4.1(9)图所示，下列图乘结果是正确的：033202201111)(1y A EI y A y A EI ++ （ ）(10) 习题4.1(10)图所示结构的两个平衡状态中，有一个为温度变化，此时功的互等定理不成立。
（ ）F CCF l(a)Pll (b)Pl习题 4.1(7)图图(b)M l /41图(a)M P l81ql 2qM 图(b)P M 图(a)102y A 3A 21A 2EI EI101y 03y习题 4.1(8)图 习题 4.1(9)图(a)(b)F Pt 12t习题 4.1(10)图【解】（1）错误。
变形体虚功原理适用于弹性和非弹性的所有体系。
（2）错误。
只有一个状态是虚设的。
（3）正确。
（4）错误。
反力互等定理适用于线弹性的静定和超静定结构。
（5）错误。
譬如静定结构在温度变化作用下，有变形但没有内力。
（6）错误。
譬如静定结构在支座移动作用下，有位移但没有变形。
（7）正确。
由桁架的位移计算公式可知。
（8）错误。
由于取0y 的M 图为折线图，应分段图乘。
（9）正确。
（10）正确。
习题4.2 填空题(1) 习题4.2(1)图所示刚架，由于支座B 下沉∆所引起D 点的水平位移∆D H =______。
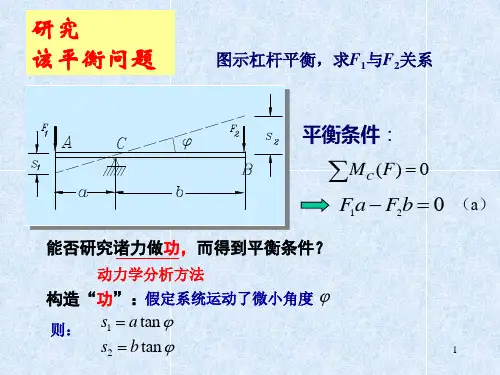
习 题4-1 如图4-19所示，在曲柄式压榨机的销钉B 上作用水平力F ，此力位于平面ABC 内，作用线平分∠ABC 。
设AB =BC ，∠ABC =θ2，各处摩擦及杆重不计，试求物体所受的压力。
图4-190δ)90cos(δδN =--︒=∑C B F s F s F W θ)90cos(δ)902cos(δθθ-︒=︒-C B s s θθsin δ2sin δC B s s = 虚位移原理0δ)90cos(δδN =--︒=∑C B F s F s F W θ 0δsin δN =-C B s F s F θθθθθtan 2)2sin(sin sin δδ2N F F s s F F C B ===4-2 如图4-20所示，在压缩机的手轮上作用一力偶，其矩为M 。
手轮轴的两端各有螺距同为h ，但方向相反的螺纹。
螺纹上各套有一个螺母A 和B ，这两个螺母分别与长为l 的杆相铰接，四杆形成棱形框，如图所示，此棱形框的点D 固定不动，而点C 连接在压缩机的水平压板上。
试求当棱形框的顶角等于2f 时，压缩机对被压物体的压力。
图4-20ϕϕcos δ)290cos(δC A s s =-︒ C A s s δsin δ2=ϕ而 θϕδπ2c o s δP s A =ϕθϕθϕtan δπsin δcos π22δPP s C ==虚位移原理0δδδN =-=∑C F s F M W θ 0tan δπδN =⨯-ϕθθPF M ϕcot πN PMF =4-3 试求图4-21所示各式滑轮在平衡时F 的值，摩擦力及绳索质量不计。
图4-21虚位移原理0δδδ=+-=∑A B F s G s F W(a) A B s s δ2δ= 2G F =(b) A B s s δ8δ= 8G F = (c) A B s s δ6δ= 6G F =(d) A B s s δ5δ= 5G F =4-4 四铰连杆组成如图4-22所示的棱形ABCD ，受力如图，试求平衡时θ应等于多少？图4-22θθcos δ)290cos(δC B s s =-︒ C B s s δsin δ2=θ 虚位移原理0δcos δ2δ=-=∑C B F s G s F W θ0sin δ2cos δ2=⨯-θθB B s G s Fθtan =GF4-5 在图4-23所示机构中，曲柄OA 上作用一力偶矩为M 的力偶，滑块D 上作用一水平力F ，机构尺寸如图。
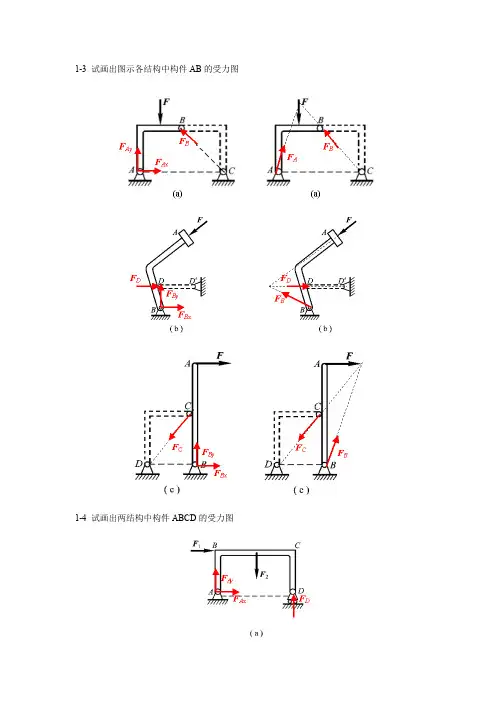
1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2，机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解：杆AB ，BC ，CD 为二力杆，受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压，分别选取销钉B 和C 为研究对象，受力如图所示：由共点力系平衡方程，对B 点有：∑=0x F 045cos 02=-BC F F对C 点有：∑=0x F 030cos 01=-F F BC解以上二个方程可得：22163.1362F F F==解法2(几何法)分别选取销钉B 和C 为研究对象，根据汇交力系平衡条件，作用在B 和C 点上的力构成封闭的力多边形，如图所示。
对B 点由几何关系可知：0245cos BC F F =对C 点由几何关系可知： 0130cos F F BC =解以上两式可得：2163.1F F =2-3 在图示结构中，二曲杆重不计，曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解：BC 为二力杆(受力如图所示)，故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用，A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示，由力偶系作用下刚体的平衡方程有（设力偶逆时针为正）：0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中：31tan=θ。
对BC 杆有：aM F F F A B C 354.0===A ，C 两点约束力的方向如图所示。
2-4FF解：机构中AB杆为二力杆，点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件，点O,C处的约束力方向也可确定，各杆的受力如图所示。
静力学第四章虚位移原理本章介绍的虚位移原理是分析静力学的理论基础，它应用功的概念建立任意质点系平衡的充要条件，是解决质点系平衡问题的最一般的原理。
虚位移原理是研究静力学问题的另一途径。
对于具有理想约束的物体系统，由于未知的约束反力不作功，应用虚位移原理求解常比列平衡方程更方便。
例如，图4-1所示的曲柄连杆机构，当要求作用在曲柄上的主动力矩M与作用在滑块上的主动力F之间的平衡关系时，用几何静力学求解，则需要分别取出曲柄、滑块为研究对象，列出平衡方程，联立求解，得到主动力之间的平衡关系，显然是十分繁琐的。
而应用虚位移原理求解系统的平衡问题时，在所列的方程中，将不出现约束反力，联立方程的数目也将减少，因而可使运算简化。
图4-1第一节虚位移与虚功的概念一、虚位移质点系内的质点，由于受到约束，它们的运动不可能是完全自由的，例如图4-2所示曲柄连杆机构，质点A只能在半径为r的圆周上运动，滑块B只能沿滑道运动，杆AB 长度不变，这样的质点系称为非自由质点系，为分析问题方便，这里把限制非自由质点系运动的条件称为约束。
图4-2在静止平衡问题中，质点系中各个质点都不动，我们设想在某质点约束允许的条件下，给其一个任意的、极其微小的位移。
在图4-2中，可设想曲柄在平衡位置上转过任一微小角度，这时A点沿圆弧切线方向有相应的位移，点B沿导轨方向有相应的位移，这些位移都是约束所允许的极微小的位移。
在某瞬时，质点系在约束允许的条件下，可能实现的任何无限小的位移称为虚位移或可能位移。
虚位移可以是线位移，也可以是角位移，虚位移用符号δ表示，以区别于实位移，如等。
必须注意，虚位移和实位移虽然都是约束所容许的位移，但二者是有区别的。
实位移是在一定的力的作用和已知的初始条件下，在一定的时间内发生的位移，具有确定的方向。
而虚位移则纯粹是一个几何概念，它既不牵涉到系统的实际运动，也不牵涉到力的作用，与时间过程和初始条件无关，在不破坏系统约束的条件下，它具有任意性。
